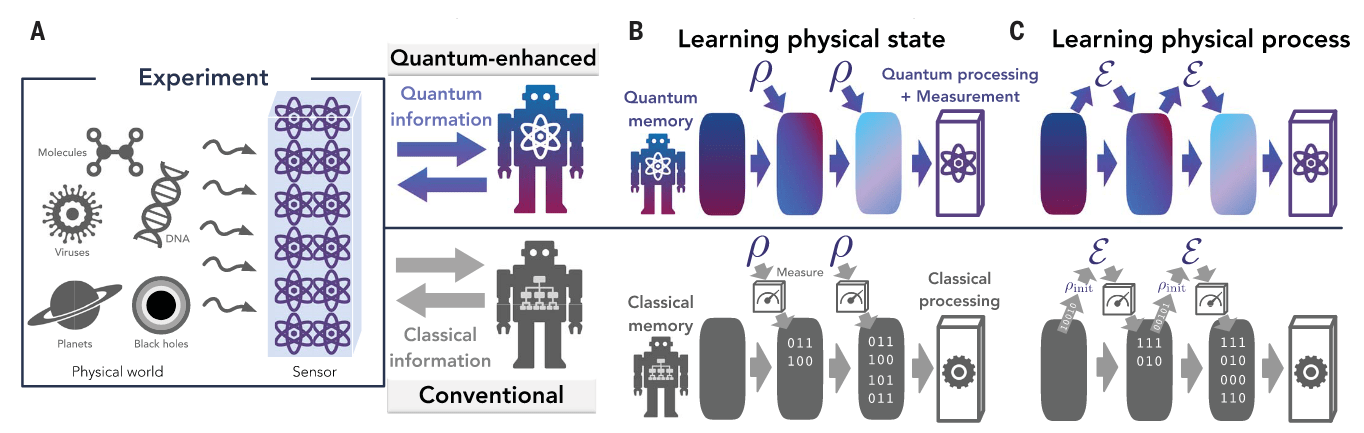
Massive quantum advantage in learning
the properties of a noisy optical channel 

 

Jonas Neergaard-Nielsen

DTU Physics

DFS annual meeting 2025
15 May, DTU

Quantum Computational advantage

Factorisation is pretty hard

2140324650240744961264423072839333563008614715144755017797754920881418023447140136643345519095804679610992851872470914587687396261921557363047454770520805119056493106687691590019759405693457452230589325976697471681738069364894699871578494975937497937  

=

64135289477071580278790190170577389084825014742943447208116859632024532344630238623598752668347708737661925585694639798853367

×  

33372027594978156556226010605355114227940760344767554666784520987023841729210037080257448673296881877565718986258036932062711

- but Shor's algorithm achieves an exponential speed-up!

Implementations of Shor's algorithm

2001:  
15 = 5 × 3

2007:  
15 = 5 × 3

2012:  
21 = 7 × 3

2019:  
35 = ? × ?...

In 2019, an attempt was made to factor the number 35 using Shor's algorithm on an IBM Q System One, but the algorithm failed because of accumulating errors.

[Wikipedia]

Quantum computational advantage

While waiting for
large-scale, fault-tolerant quantum computers,
the race is on to achieve

of (almost) useless problems...

Quantum computational advantage

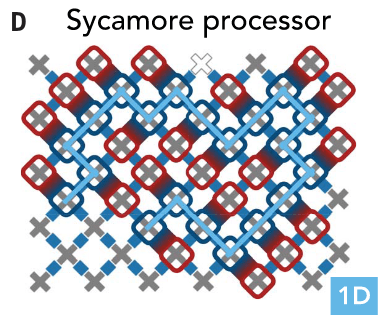
Google - random circuit sampling

Arute et al., Quantum supremacy using a programmable superconducting processor, Nature 574, 505 (2019)

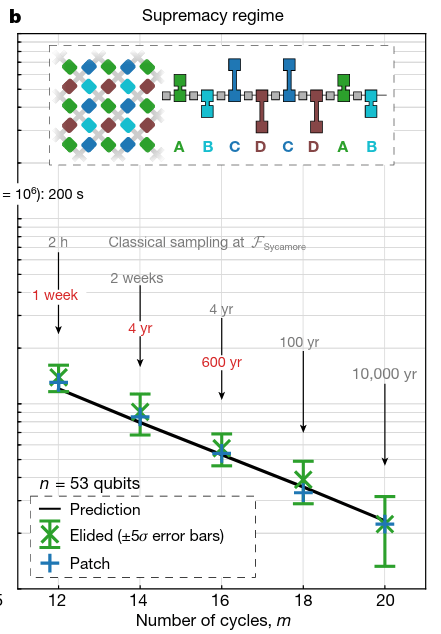
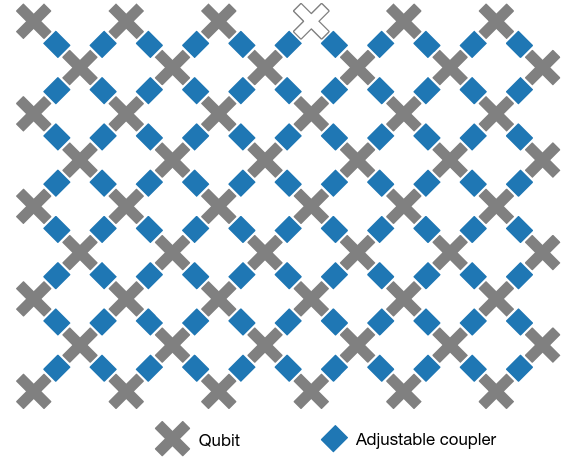
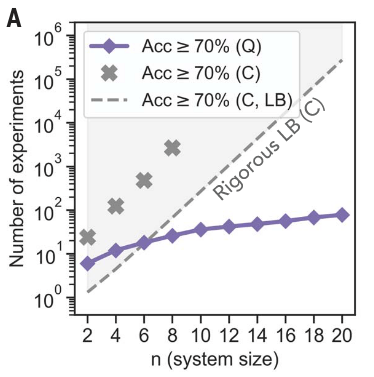
Quantum computational advantage

Pan et al., Solving the sampling problem of the Sycamore quantum circuits, Phys. Rev. Lett. 129, 090502 (2022)

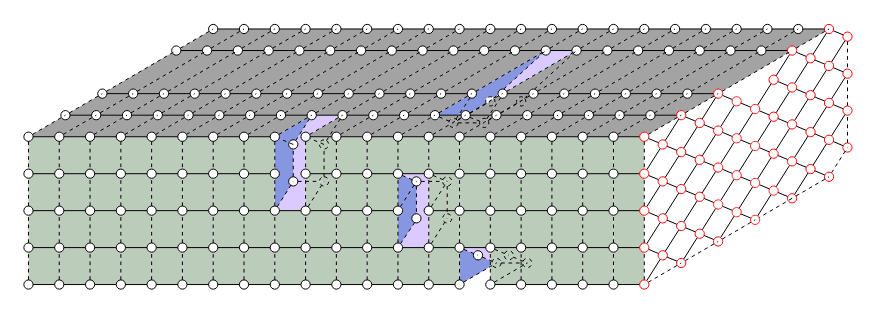
Using our algorithm the simulation for the Sycamore circuits with n = 53 qubits and m = 20 cycles is completed in about 15 hours using 512 V100 GPUs.

Quantum computational advantage

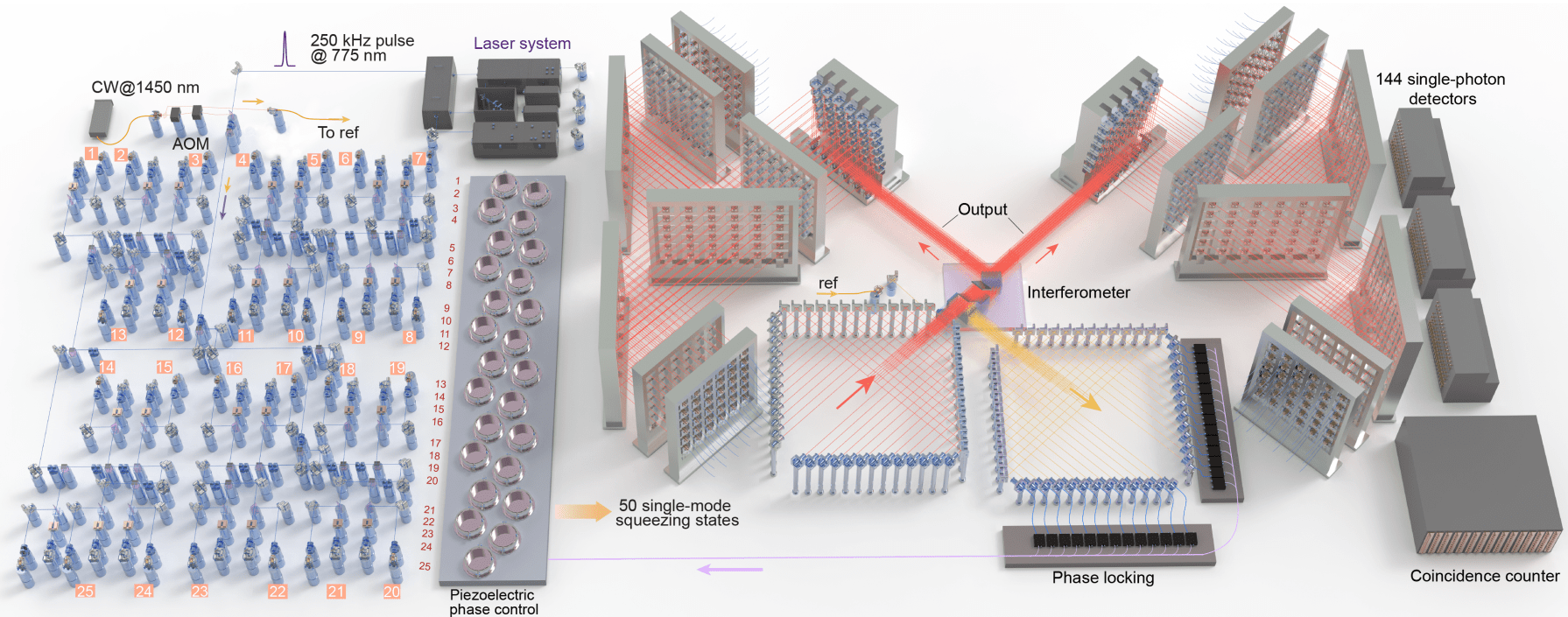
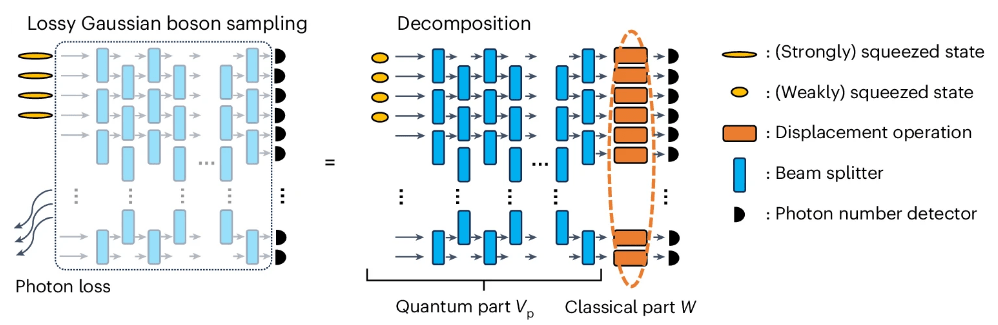
USTC - Gaussian boson sampling

Zhong et al., Quantum computational advantage using photons,
Science 370, 1460 (2020)   +  Zhong et al., Phys. Rev. Lett., 127, 180502 (2021)

Quantum computational advantage

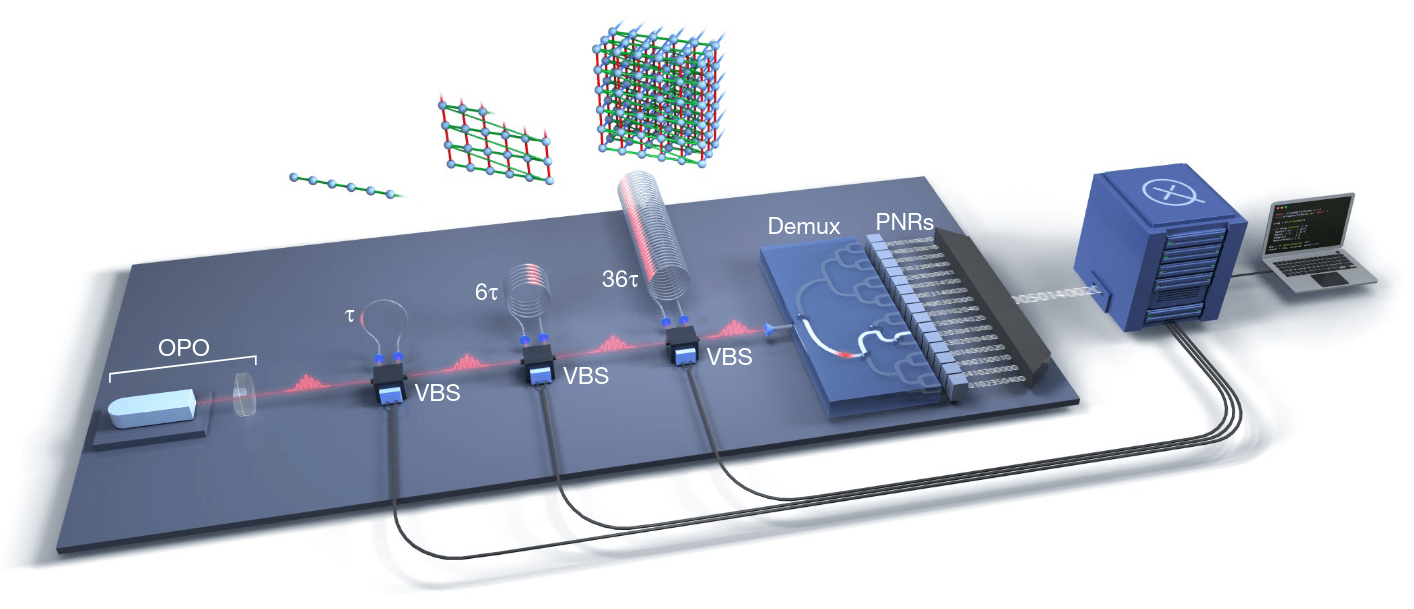
Xanadu - Gaussian boson sampling

Madsen et al., Quantum computational advantage with a programmable photonic processor, Nature 606, 75 (2022)

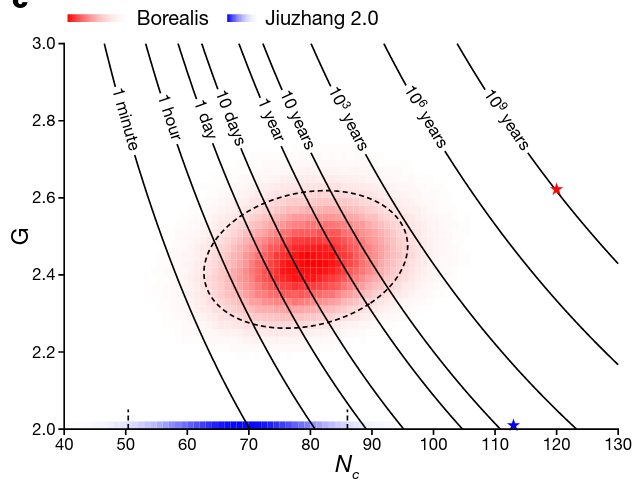
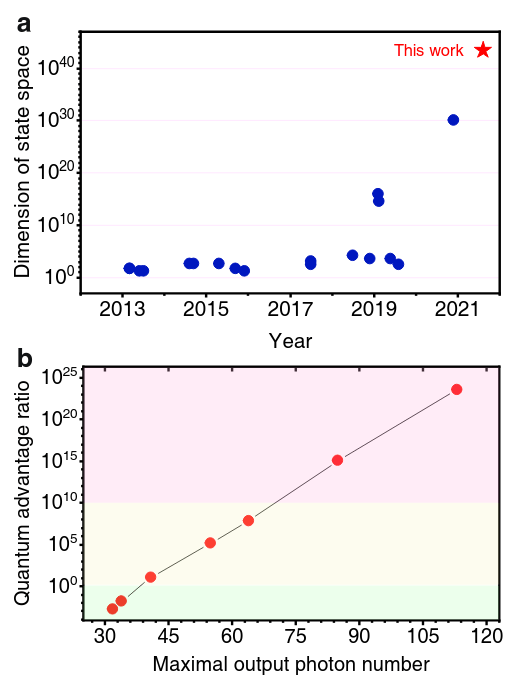
Quantum computational advantage

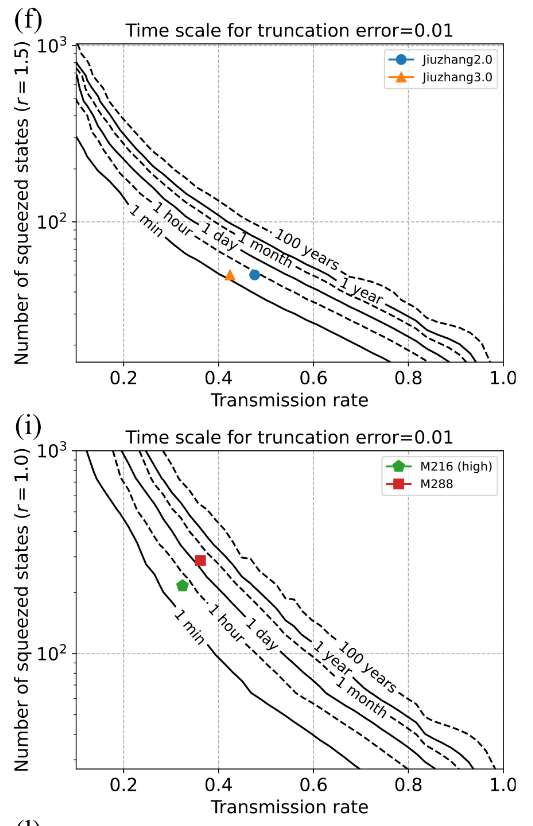
Oh et al., Classical algorithm for simulating experimental Gaussian boson sampling, Nat. Phys. 20, 1461 (2024)

Quantum computational advantage

LaRose, arXiv:2412.14703

Quantum Learning advantage

Process learning

\Lambda

probe / input data

unknown process

\{\rho_i \}_{_N}
\{x_i\}_{_N}

measurement
data

\tilde\Lambda

estimate

Very general scenario:

Learn a physical process by interacting with a known probe + measurement system.

Goal: to be able to predict future interactions, discriminate between channels, etc.

Quantum learning advantage

probe / input data

unknown process

measurement
data

estimate

Entangled probes + collective measurement can overcome limitations imposed by quantum noise, considerably improving the sample complexity (scaling of \(N\) vs. system size)

\Lambda
\{\rho_i \}_{_N}
\{x_i\}_{_N}
\tilde\Lambda

TL;DR

We learn the physical properties of a

random displacement channel

using

entanglement and collective measurement

to obtain 9 orders of magnitude

provable quantum advantage

\Lambda
\rho_i
x_i
\tilde\Lambda
\{\ \ \ \}_{_N}
\{\ \ \ \}_{_N}

Huang et al., Science 376, 1182 (2022)

Quantum learning advantage

We proved that schemes exploiting entanglement with an ancillary quantum memory can learn n-mode random displacement channels with exponentially fewer samples compared to entanglement-free schemes.

Quantum learning advantage

Random displacement channel

Random displacement channel

???

Random displacement channel

In this context:  a bosonic channel

\hat\rho'=\Lambda(\hat\rho)

Input: state of
a bosonic system

Output: modified state
(possibly at a different location)

\hat\rho

(light, mechanical oscillator, microwave resonator, ...)

Random displacement channel

Credit: ESO/Y. Beletsky

Random displacement channel

Random displacement channel

Random displacement channel

phase space

Random displacement channel

phase space

Random displacement channel

phase space

quadrature variables

Random displacement channel

[\hat x,\hat p]=i\hbar
\Delta x \Delta p \ge \frac{\hbar}{2}

Random displacement channel

Random displacement channel

Random displacement channel

Random displacement channel

Random displacement channel

Random displacement channel

Phase space displacement:

  • not as natural as phase/amplitude noise
  • but certain processes can be mapped to displacement - tilt/shift of laser beam, tailored noise models, etc.

Here:

  • theoretical and practical convenience
  • fundamental interest

Random displacement channel

\hat\rho \rightarrow \underbrace{\hat D(\alpha) \hat\rho \hat D^\dagger(\alpha)}_{\Lambda(\hat\rho)}

Constant displacement:

unitary operation

Random displacement channel

Random displacement:

different for every use of the channel

Random displacement channel

Random displacement:

given by a probability distribution p(α) 

\hat\rho \rightarrow \underbrace{ \int d^2\alpha \ p(\alpha) \hat D(\alpha) \hat\rho \hat D^\dagger(\alpha)}_{\Lambda(\hat\rho)}

The task, the challenge

Learn an unknown distribution p(α)

        describing the channel Λ

                by probing N times

                        and processing the data {x\({}_i\)}

\Lambda / p(\alpha)
\{\rho_i \}_{_N}
\{x_i\}_{_N}
\tilde\Lambda / \tilde p(\alpha)
p(\alpha)

Most obvious approach:

  • vacuum state as probe
  • double homodyne (heterodyne) measures both x and p - but limited by vacuum noise

The task, the challenge

x

p

[\hat x,\hat p]=i\hbar

Quantum entanglement (two-mode squeezed state) improves sensitivity arbitrarily

  • The probe is correlated with an un-displaced "memory" 
  • Joint variables commute ⇒ no quantum noise

Going quantum

x' = x₁ - x₂

p' = p₁ + p₂

[\hat x_1 - \hat x_2,\hat p_1 + \hat p_2]=0

x₁ , p₁

x₂ , p₂

Going quantum - example

Truth

Distributions with narrow features are harder to resolve

←Example p(α) with oscillations in x and p

Going quantum - example

Truth

Distributions with narrow features are harder to resolve

←Example p(α) with oscillations in x and p

Instead of p(α), we mostly consider its Fourier transform (the characteristic function) - simplifies theory a bit

\lambda(\beta) = \int d^2\alpha\ p(\alpha)e^{\alpha^\dagger\beta - \beta^\dagger\alpha}

Going quantum - example

Truth

vacuum + heterodyne

Distributions with narrow features are harder to resolve

Going quantum - example

Truth

vacuum + heterodyne

entanglement-assisted

making it spicy

So far, just a single bosonic mode:

ordinary small-factor sensitivity enhancement from squeezing

making it spicy

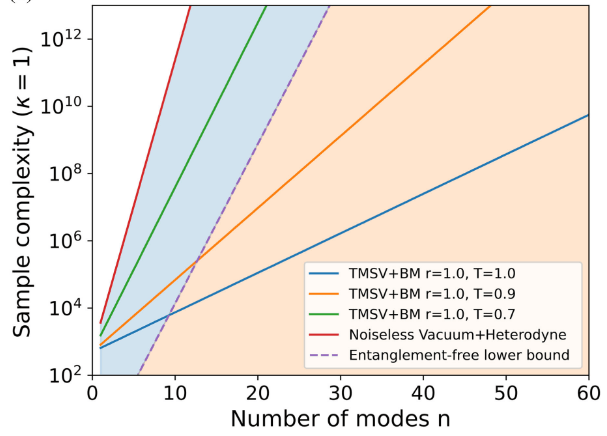
With n >> 1 modes, correlated noise becomes super hard to reconstruct

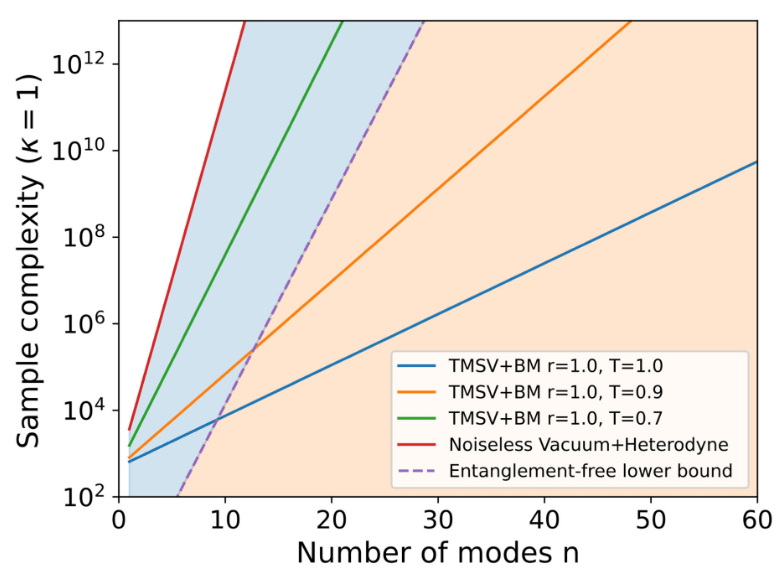
making it spicy

The sample complexity (how many samples needed for precise estimation) is exponential in n

N \propto e^{2n}
N \propto 3^{n}
N \propto e^{2e^{-2r}n}

- but dramatically "less exponential" with entanglement (squeezing parameter r).

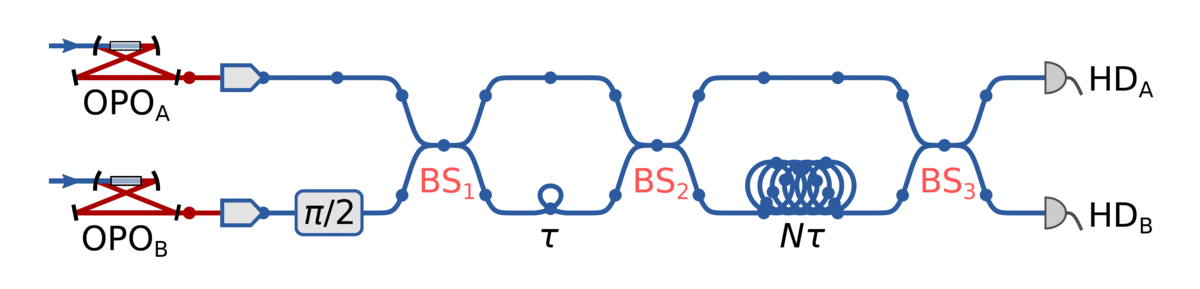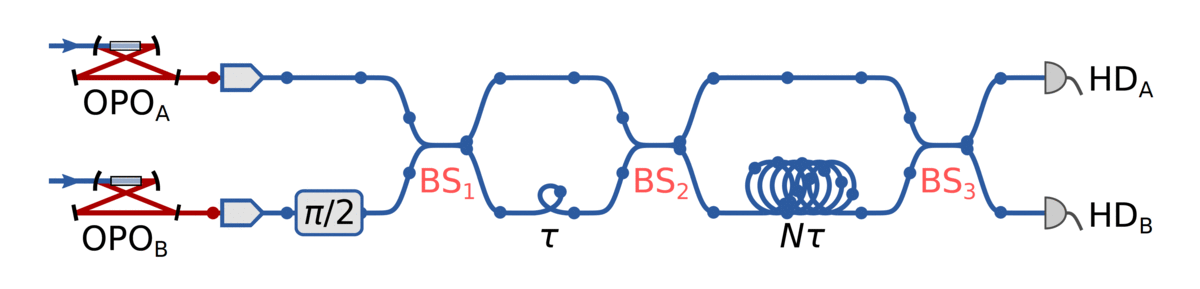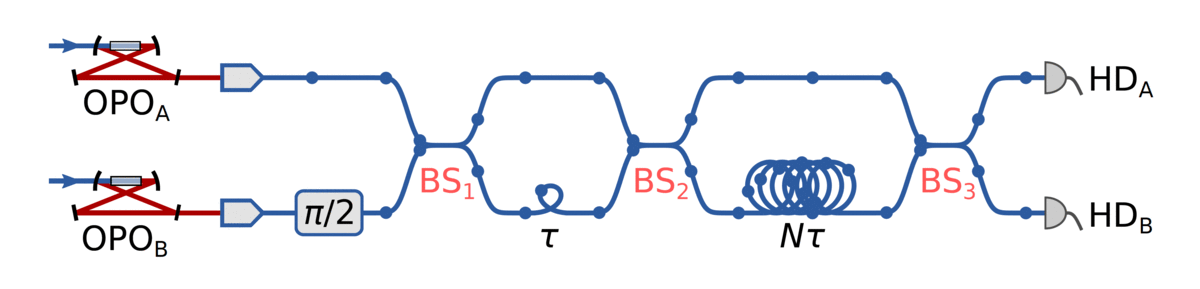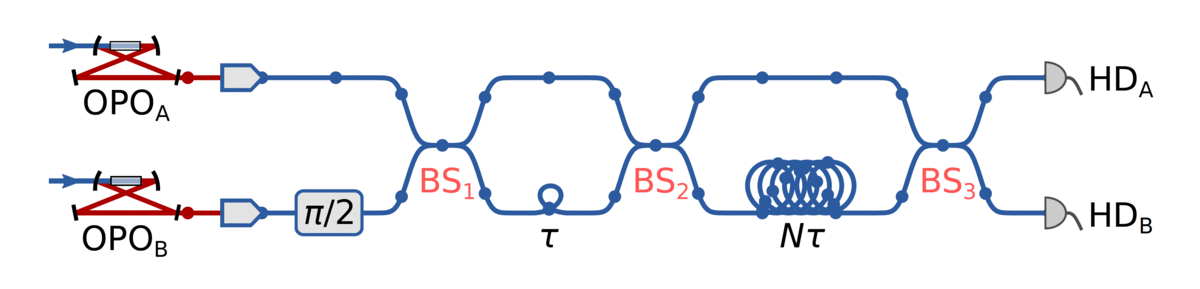
Down to the lab!

Using temporal modes makes scaling to many modes easier

p(α) samples

squeezing: 5.0 dB

efficiency: 79%

Channel reconstruction

n = 16

n = 30

Channel reconstruction

~ 20 min

~ 20 Myr

Hypothesis test

# classical samples needed to get same success probability as quantum

Hypothesis test

rigorous 

9-orders of mag.

quantum advantage

# classical samples needed to get same success probability as quantum

TL;DR

We learn the physical properties of a

random displacement channel

using

entanglement and collective measurement

to obtain 9 orders of magnitude

provable quantum advantage

\Lambda
\rho_i
x_i
\tilde\Lambda
\{\ \ \ \}_{_N}
\{\ \ \ \}_{_N}

Zhenghao Liu

Romain Brunel

Emil Østergaard

Oscar Cordero

Jens Nielsen

Axel Bregnsbo

Ulrik Andersen

+ Chicago / Caltech / Waterloo / KAIST collaborators:

John Preskill, Liang Jiang, Changhun Oh,
Hsin-Yuan Huang, Sisi Zhou, Yat Wong, Senrui Chen

Oh, Chen, et al., Phys. Rev. Lett. 133, 230604 (2024)

Liu, Brunel, et al., arXiv:2502.07770

Teaser:  Photonic quantum computing technology

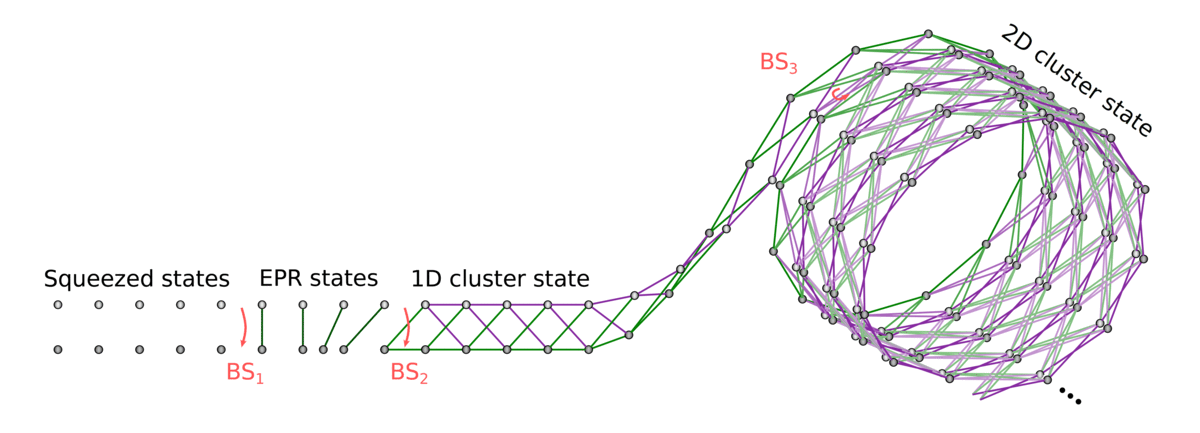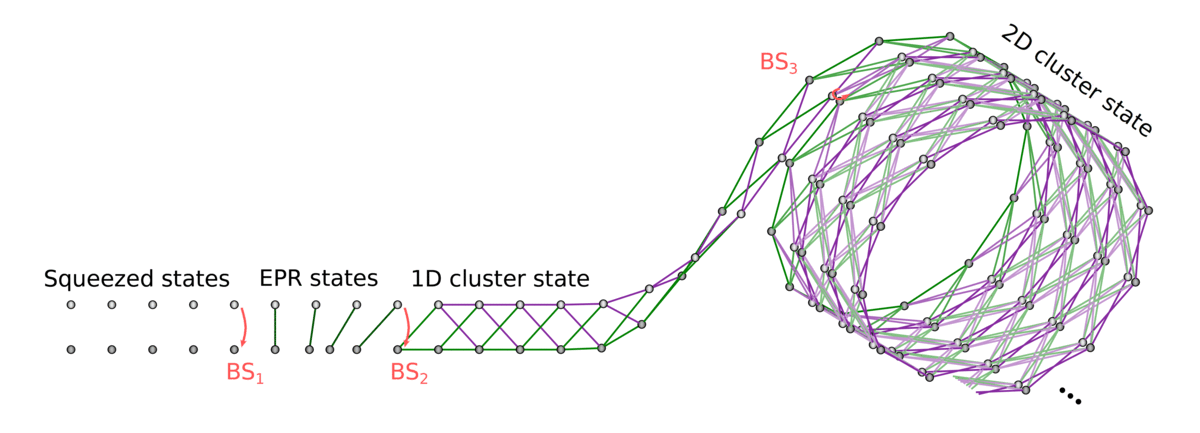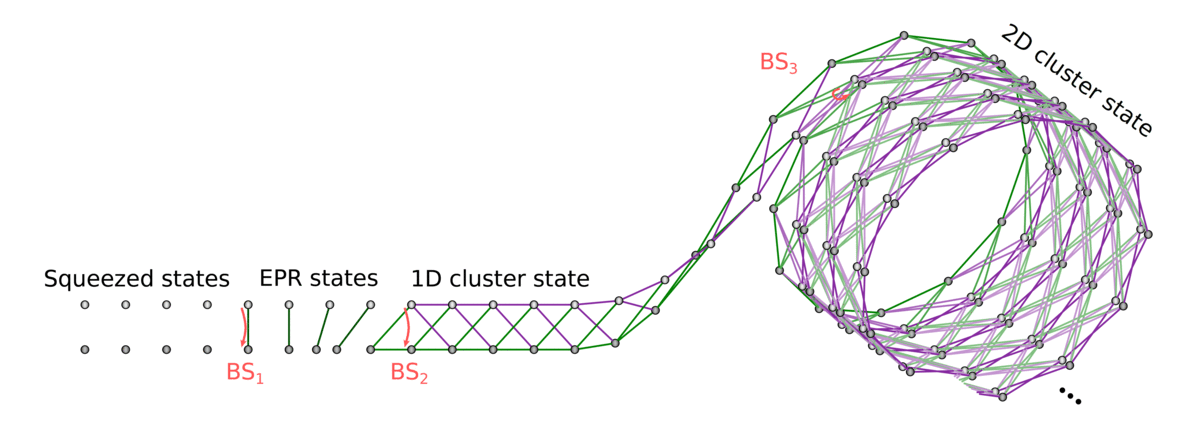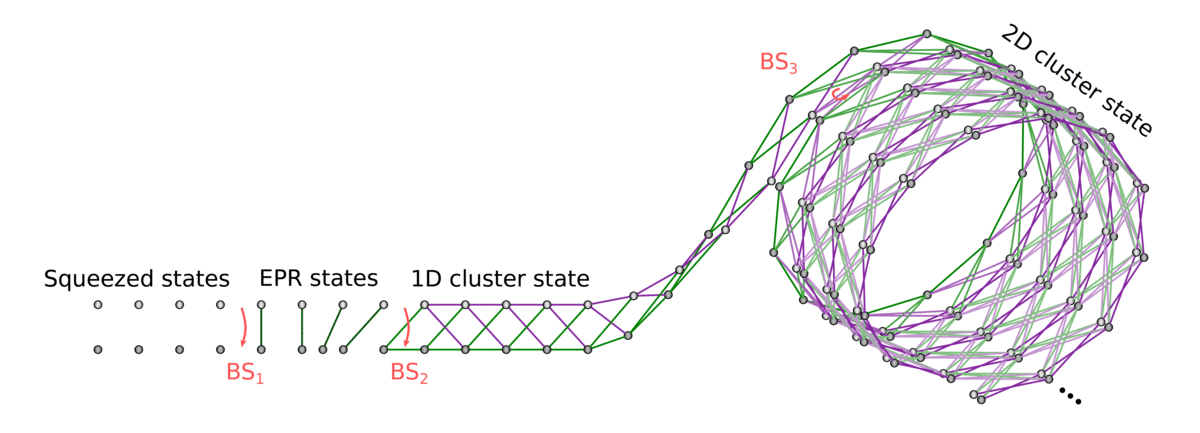
Gaussian boson sampling

Measurement-based
quantum computing

Teaser:  Photonic quantum computing technology

Gaussian boson sampling

Measurement-based
quantum computing

Abhi

Renato

Donghwa

Asger

squeezing on chip

measurement-induced interferometers

GKP qubits

MBQC programming

Thanks!