

An optical platform for measurement-based quantum computing
Jonas S. Neergaard-Nielsen
bigQ - Center for Macroscopic Quantum States
Technical University of Denmark (DTU)



Main credits: Mikkel Vilsbøll Larsen - now at Xanadu
Outline
- Continuous-variable Measurement-based Quantum Computing
- Cluster state generation
- Gate implementation
- Scheme for fault-tolerant computing
CV-MBQC



Crazy Cryogenics + individual qubit control
= pretty hard to scale up...
F. Arute et al., Nature 574, 505 (2019)
53 qubit sampling
Photonic quantum computing advantages:
- mostly room temperature (except detectors)
- potentially better scalability
- direct network-compatibility
Challenges:
- photonic qubits don't like to stick around
- photonic qubits don't like to interact
→ use measurement-based quantum computing
instead of standard gate-based approach


Y. Wu et al., Phys. Rev. Lett. 127, 180501 (2021)
H-S. Zhong et al., Phys. Rev. Lett. 127, 180502 (2021)
56 qubit sampling
144 mode, 113 photons Gaussian Boson Sampling
Standard GATE MODEL of quantum computation





Measurement-based quantum computing (MBQC)

Measurement-based quantum computing (MBQC)


Photonics is ideally suited for this!
Coherent, high-fidelity qubit interactions
Creation of massively entangled cluster state
- the "computational substrate"
challenge:
Continuous-variable MBQC
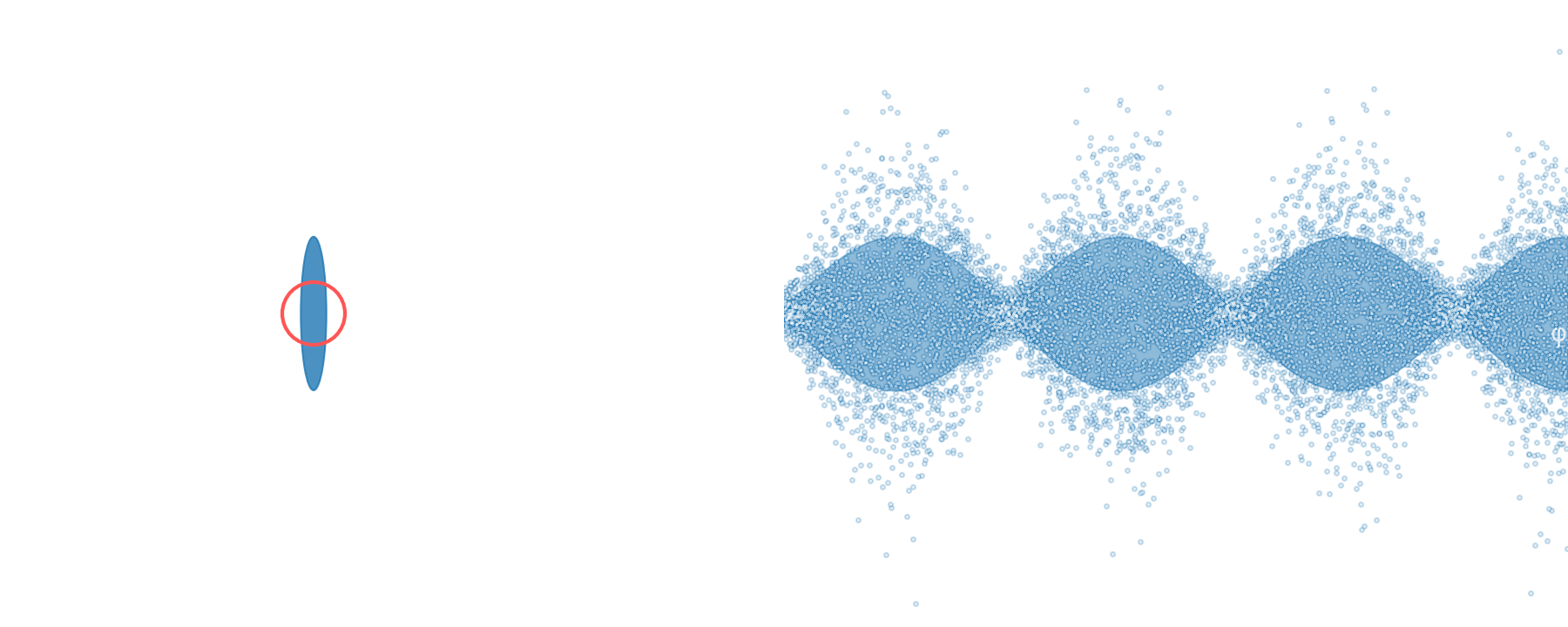
squeezed states
beam splitters


homodyne detection
Cluster state: graph state with regular lattice adjacency matrix \(\mathbf{A}\).
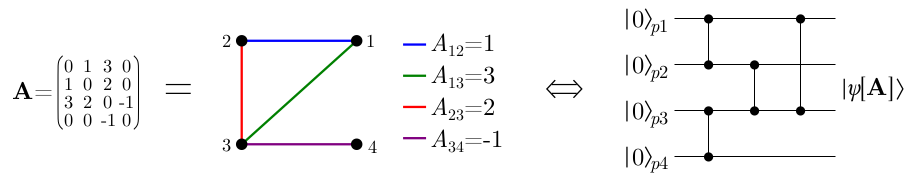
In CV:
nodes
edges
Fullfils the nullifier condition: \((\mathbf{\hat{p}} - \mathbf{A}\mathbf{\hat{x}})\ |\psi_\mathbf{A}\rangle=0\)
Finite squeezing → self-loops (non-zero, complex-valued diagonal in \(\mathbf{A}\))
Our work is inspired by
- theory from Nicolas Menicucci's group
- experiments from Akira Furusawa's group




Wallace & Gromit: The Wrong Trousers (1993)
Menicucci et al., PRL 104, 250503 (2010)

Uses temporal encoding:
- resources are re-used over and over
- computation is performed in parallel with generation of the cluster state
Cluster state generation
S. Yokoyama et al., Nat. Photonics 7, 982 (2013)

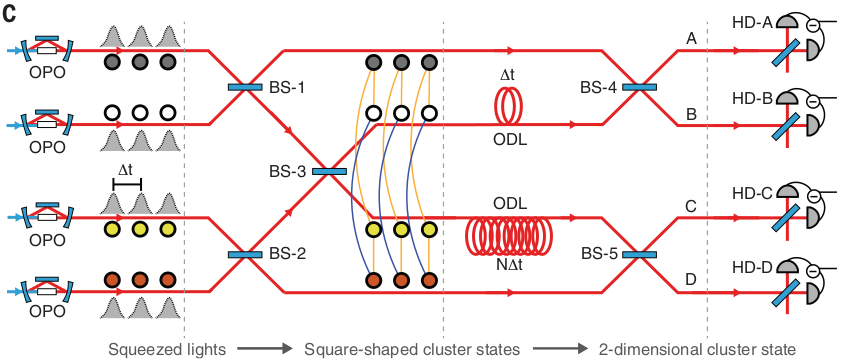
Generate 1D cluster state following Yokoyama et al.:
- Produce an x-squeezed and a p-squeezed state
- Generate EPR state by combining them on a 50:50 BS
- Delay one mode by a predefined delay time \(\tau\)
- Entangle neighbouring EPR states by interfering on another 50:50 BS
Then, generate cylindrical cluster state (~2D) by "coiling up" the 1D string and stitching together


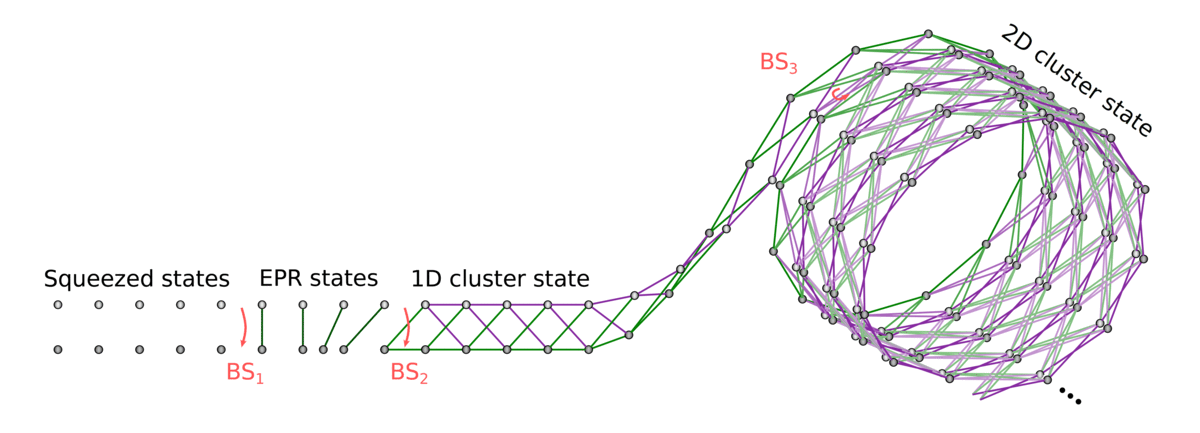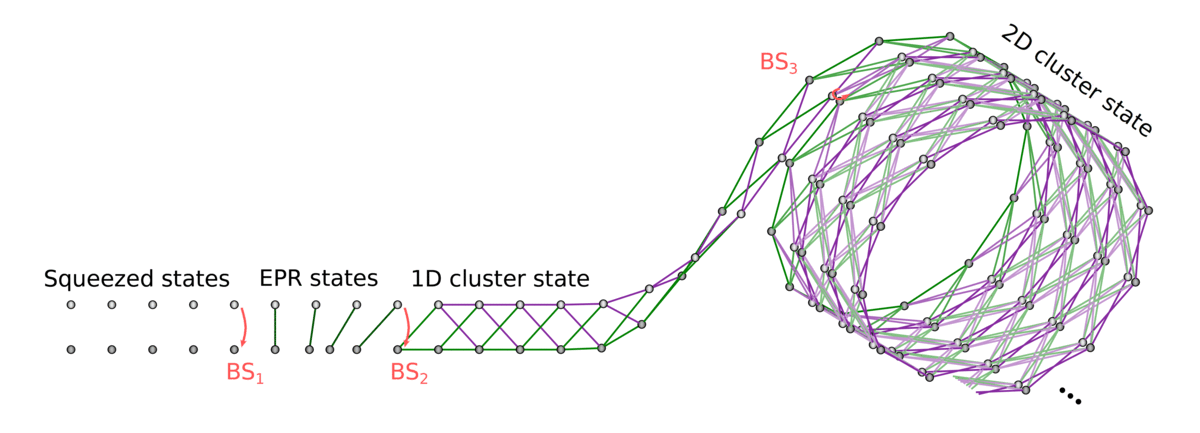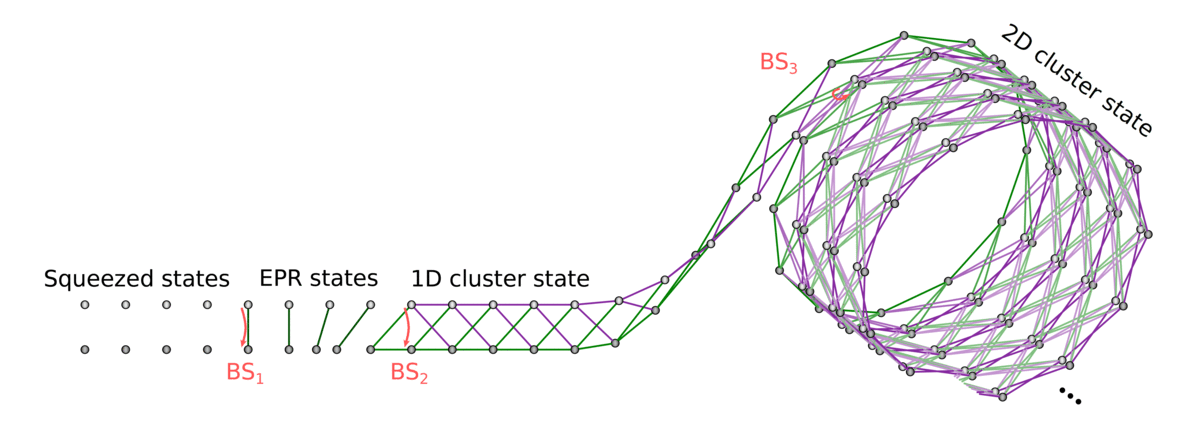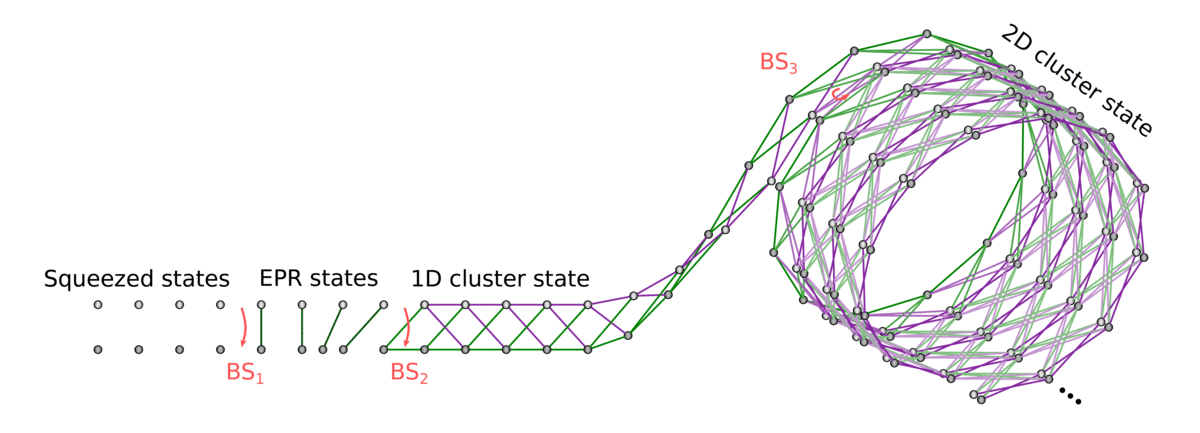
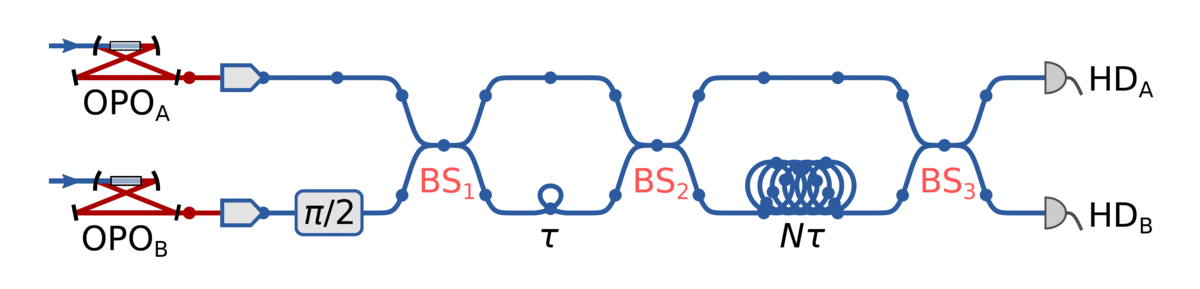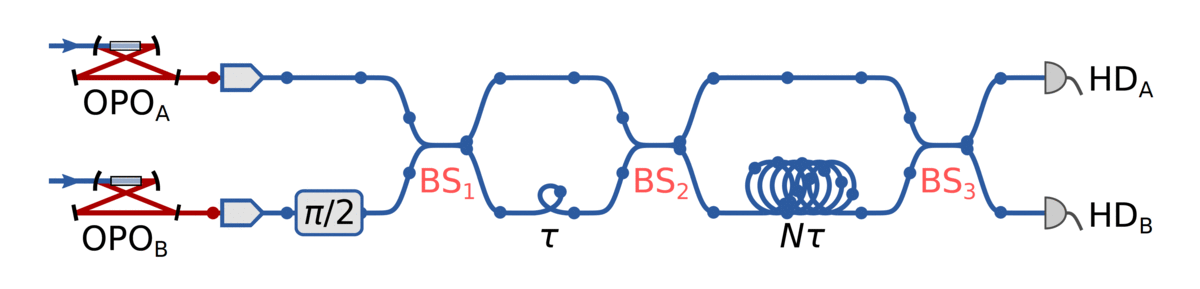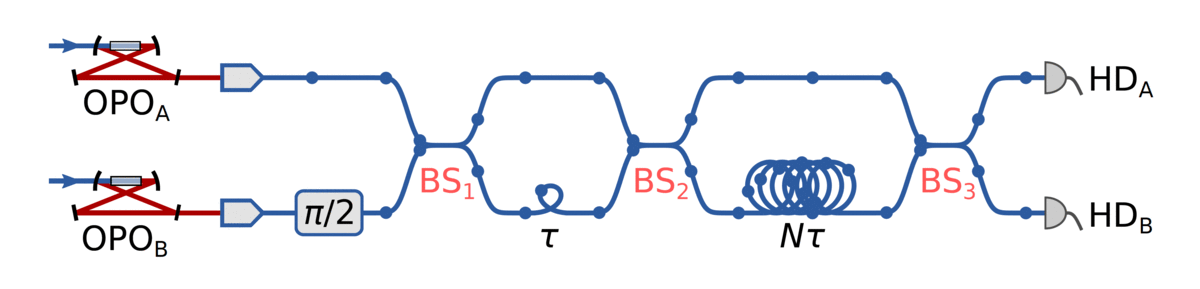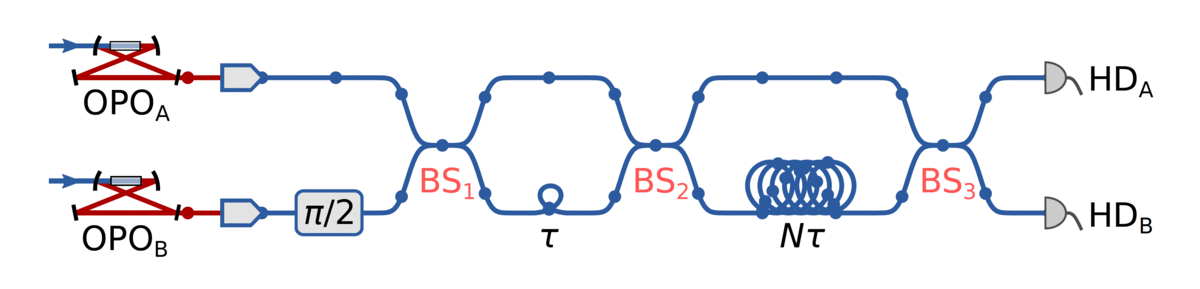




EPR adjacency matrix:
\(\mathbf{Z}_\mathrm{EPR} = \begin{pmatrix}i \cosh 2r & -i\sinh 2r \\ -i\sinh 2r & i\cosh 2r\end{pmatrix}\)
BS₂ induces new graph edges
\(\mathbf{Z}_\mathrm{1D}\) is not a true cluster state,
but a phase shift of \(\pi/2\) on every 2nd mode transforms it to \(\mathbf{Z}'_\mathrm{1D}\), a true (approximate) cluster state


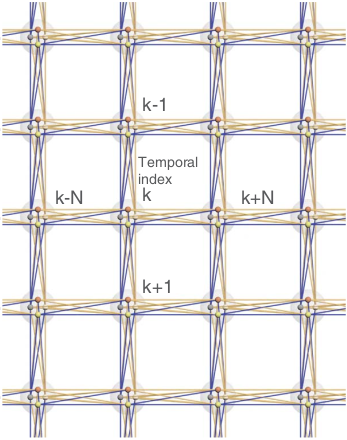
Long delay makes nodes separated by \(N=12\) temporal modes adjacent
BS₃ now connects the graph in the second dimension






Nullifiers of the 2D graph state:
\(\hat{n}_k^x=\hat{x}_{k}^A+\hat{x}_{k}^B-\hat{x}_{k+1}^A-\hat{x}_{k+1}^B-\hat{x}_{k+N}^A+\hat{x}_{k+N}^B-\hat{x}_{k+N+1}^A+\hat{x}_{k+N+1}^B\)
\(\hat{n}_k^p=\hat{p}_{k}^A+\hat{p}_{k}^B+\hat{p}_{k+1}^A+\hat{p}_{k+1}^B-\hat{p}_{k+N}^A+\hat{p}_{k+N}^B+\hat{p}_{k+N+1}^A-\hat{p}_{k+N+1}^B\)
\(k+1\)
\(k\)
\(k+N+1\)
\(k+N\)
with variance \(\langle\Delta\hat{n}_k^{x2}\rangle=4e^{-2r_A},\quad\langle\Delta\hat{n}_k^{p2}\rangle=4e^{-2r_B}\)
The 8 modes making up the nullifiers constitute a unit cell of the graph.
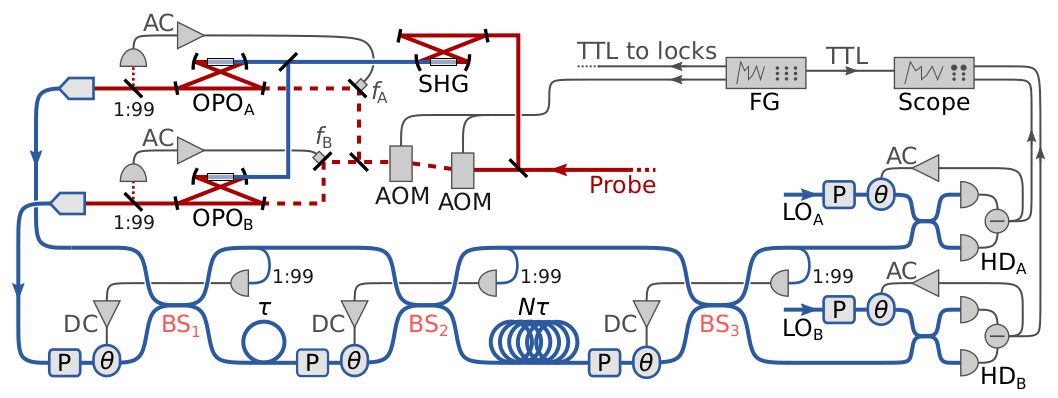
Experiment in more detail
λ = 1550 nm: squeezed light generation in free space, the rest in fibre
3 cavity locks + 7 phase locks (chopped)
50 m fibre = 247 ns delay
600 m fibre

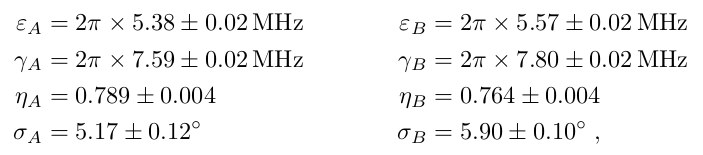
Laser is cw; homodyne power spectra reveal detailed experimental parameters

We define "pulses" as temporal modes optimised for high squeezing
But how can we be sure the state is entangled (more precisely: inseparable)?

\(k+1\)
\(k\)
\(k+N+1\)
\(k+N\)
van Loock-Furusawa criterion for bipartition of \(S\):
- Define operators \(\displaystyle\hat{X} = \sum_{j\in S} h_j\hat{x}_j,\quad \hat{P} = \sum_{j\in S} g_j \hat{p}_j\)
- If \(\{h_j\},\{g_j\}\) exist such that
then \(\mathcal{S}_1\) and \(\mathcal{S}_2\) are inseparable
Periodic, so enough to show inseparability of a unit cell
Complete inseparability: any bipartition is inseparable

Task: find suitable \(\hat{X}, \hat{P}\) for all 127 possible bipartitions of the 8-mode unit cell
\(\displaystyle \langle\Delta\hat{X}^2\rangle + \langle\Delta\hat{P}^2\rangle < \Big|\sum_{j\in \mathcal{S}_1} h_j g_j\Big| + \Big| \sum_{j\in\mathcal{S}_2} h_j g_j\Big|\)
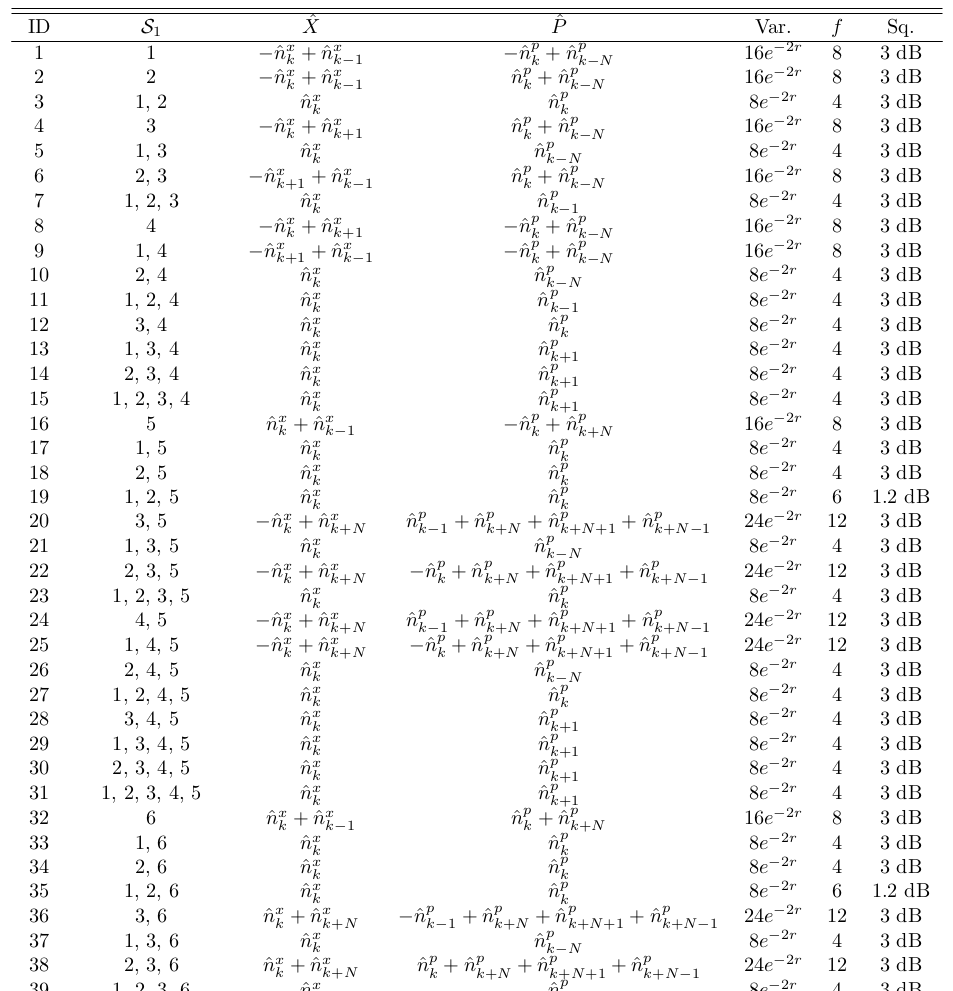
We find linear combinations of nullifiers as \(\hat{X}\) and \(\hat{P}\) for all 127 bipartitions of the unit cell
van Loock-Furusawa criterion is fulfilled if all nullifiers are squeezed by >3 dB

\(\displaystyle \langle\Delta\hat{X}^2\rangle + \langle\Delta\hat{P}^2\rangle < \Big|\sum_{j\in \mathcal{S}_1} h_j g_j\Big| + \Big| \sum_{j\in\mathcal{S}_2} h_j g_j\Big|\)
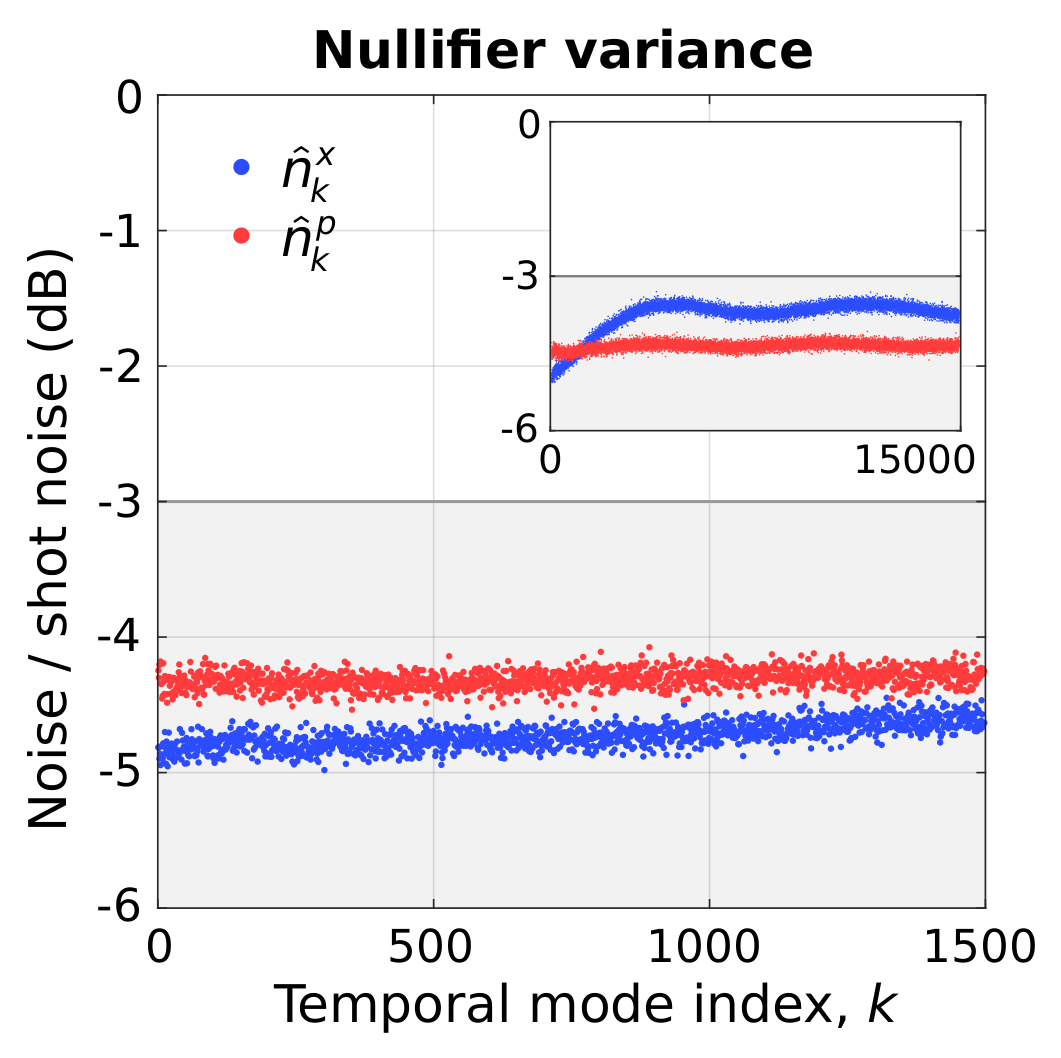

Complete inseperability confirmed for 2 × 15000 modes

Science 366, 369–372 (2019)
Gate implementation


To implement gates and circuits on a cluster state, it is reshaped into "wires":
Measuring a node in the computational basis removes it from the graph
With our \(N=12\) cylindrical graph,
we can project out 6 wires

Computational scheme
- Wires consist of 2-mode EPR states
- Gates implemented by teleportation
- Gates determined by homodyne phases
- Simpler now to consider BS₃ as part of a joint measurement on a 1D cluster

Computational scheme
- Wires consist of 2-mode EPR states
- Gates implemented by teleportation
- Gates determined by homodyne phases
- Simpler now to consider BS₃ as part of a joint measurement on a 1D cluster

Computational scheme
\(\hat{U}=(-1)^w\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\hat{S}\left(\tan\frac{\theta_{-,k}}{2}\right)\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\)
\(\theta_{\pm,k}=\pm\theta_{A,k}+\theta_{B,k}\)
Implemented gate:
Computational scheme

\(\hat{U}=(-1)^w\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\hat{S}\left(\tan\frac{\theta_{-,k}}{2}\right)\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\)
\(\theta_{\pm,k}=\pm\theta_{A,k}+\theta_{B,k}\)
Single-mode gates
\(\mathbf{\hat{q}'} = \mathbf{U \hat{q}} + \mathbf{N\hat{p}_i} + \mathbf{Dm} \)
Side effects of the gate teleportation:
Noise from finite squeezing
- achilles heel of CV-MBQC!
Measurement outcome-dependent displacement
- can be treated in post-processing

Both \(\mathbf{U}\) and \(\mathbf{N}\) can be characterised by gate tomography
(W. Asavanant et al., PR Applied 16, 034005 (2021))
- use correlations between output and reference input (entangled with input)

Carefully calibrated AWG (arbitrary waveform generator) + EOMs (phase shifters) implement fully programmable phase settings


frames of 228 modes - allows for full characterisation of 8 single-mode gates
\(\hat{U}=(-1)^w\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\hat{S}\left(\tan\frac{\theta_{-,k}}{2}\right)\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\)
\(\theta_{\pm,k}=\pm\theta_{A,k}+\theta_{B,k}\)
Implemented single-mode gates


Rotation
\(\hat{U}=(-1)^w\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\hat{S}\left(\tan\frac{\theta_{-,k}}{2}\right)\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\)
\(\theta_{\pm,k}=\pm\theta_{A,k}+\theta_{B,k}\)
Implemented single-mode gates
Shear


- actually \(\hat F^j\hat P(\sigma)\) since \(\hat P(\sigma)\) cannot be done in one step
\(\hat{U}=(-1)^w\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\hat{S}\left(\tan\frac{\theta_{-,k}}{2}\right)\hat{R}\left(\frac{\theta_{+,k}}{2}\right)\)
\(\theta_{\pm,k}=\pm\theta_{A,k}+\theta_{B,k}\)
Implemented single-mode gates
Squeezing


Two-mode gate

Small circuit

MV Larsen, X Guo, CR Breum, JS Neergaard-Nielsen, UL Andersen
Nature Physics 17, 1018 (2021)
\(\lbrace\hat{R}(\theta),\hat{S}(e^r),\hat{C}_Z(g)\rbrace\)
is a universal multi-mode Gaussian gate set.

\(\lbrace\hat{F}=\hat{R}(\pi/2),\hat{P}(1),\hat{C}_Z(g)\rbrace\)
is a multi-mode Clifford gate set for GKP-encoded qubits
Scheme for fault-tolerance
MV Larsen, C Chamberland, K Noh, JS Neergaard-Nielsen, UL Andersen
PRX Quantum 2, 030325 (2021)
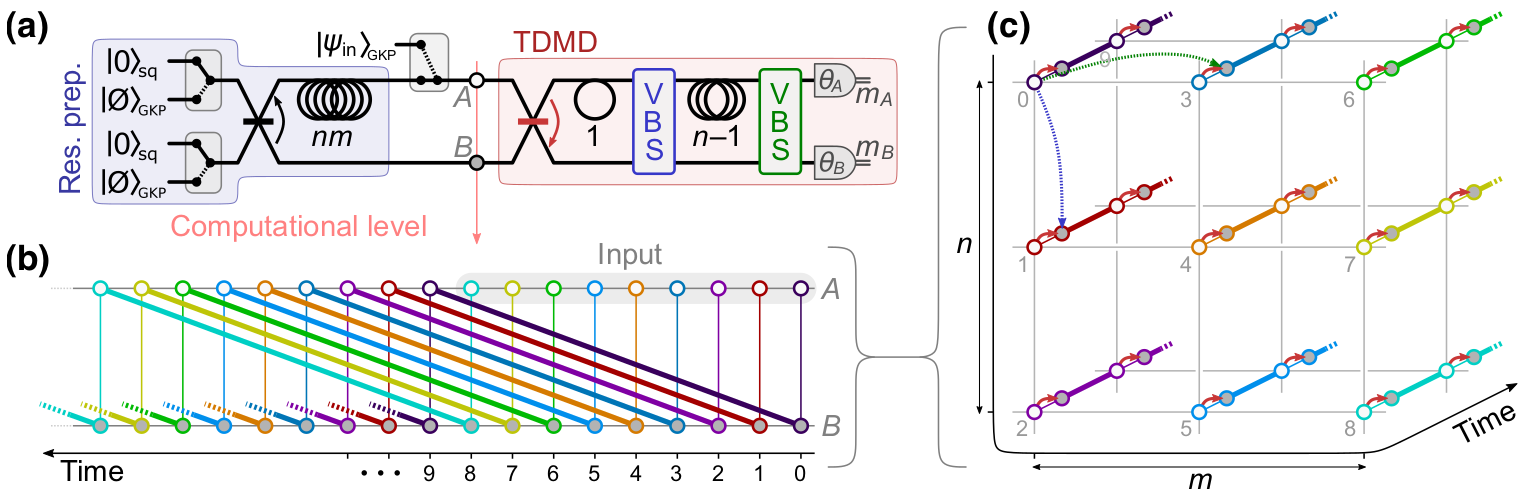
Similar platform, but modified architecture
- supply of GKP states enables bosonic error correction
- EPR wires in 2D grid allows for encoding topological qubits
- variable beam splitters in the measurement device implement 2-mode gates
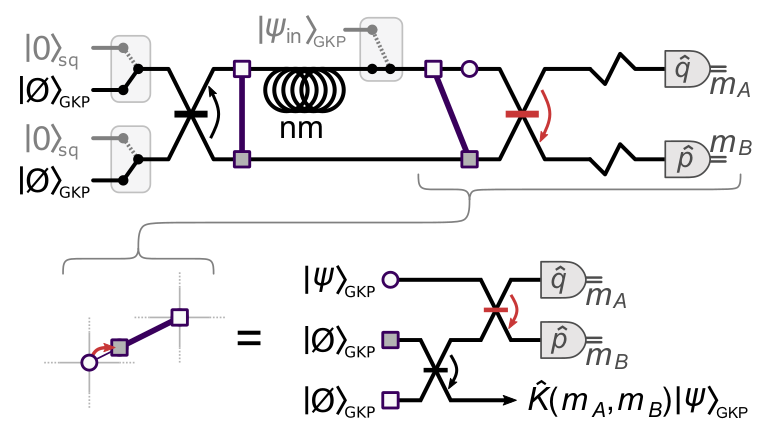
Bosonic error correction with GKP naught states - requires only Gaussian gates.
Feed-forward of measurement results only required for non-Clifford gates
Non-Clifford T gate can be made from GKP magic state inputs
(Walshe et al., PRA 102, 062411 (2021))
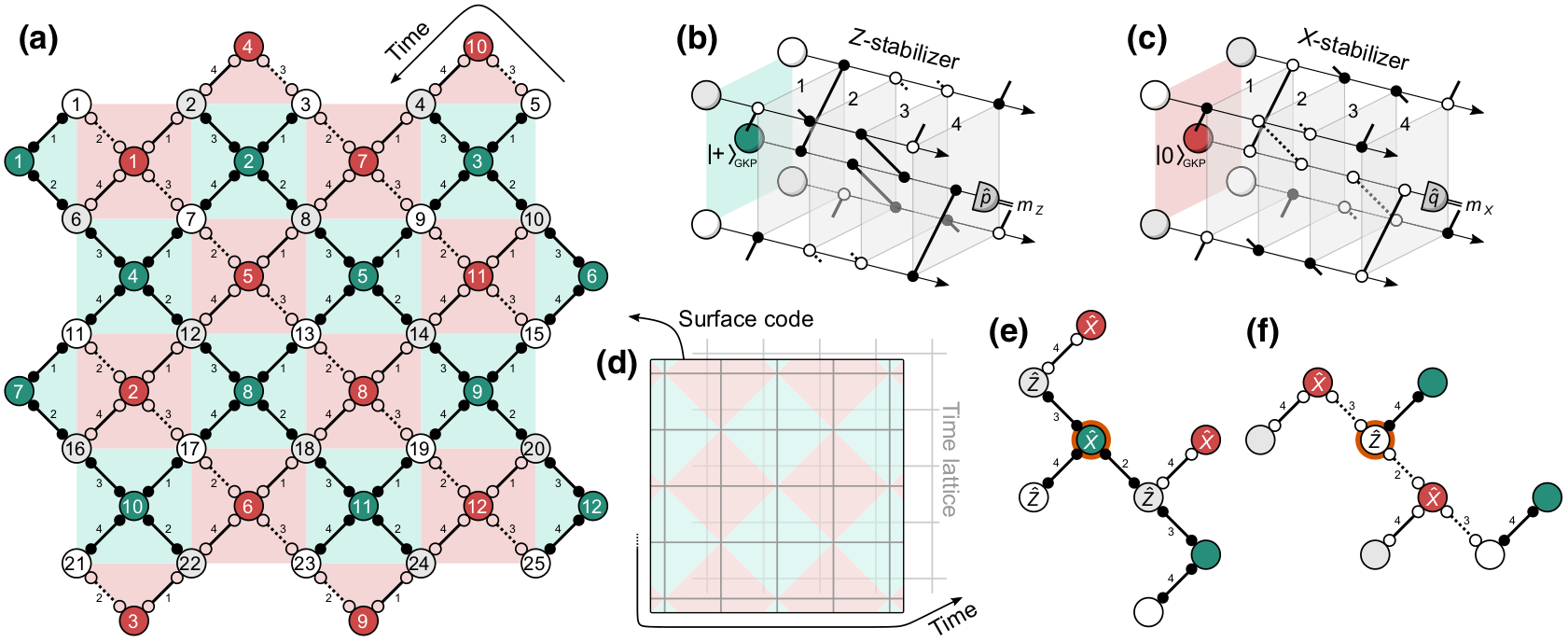
At the qubit level, error correction by surface code
GKP error correction between every stabilizer measurement gate
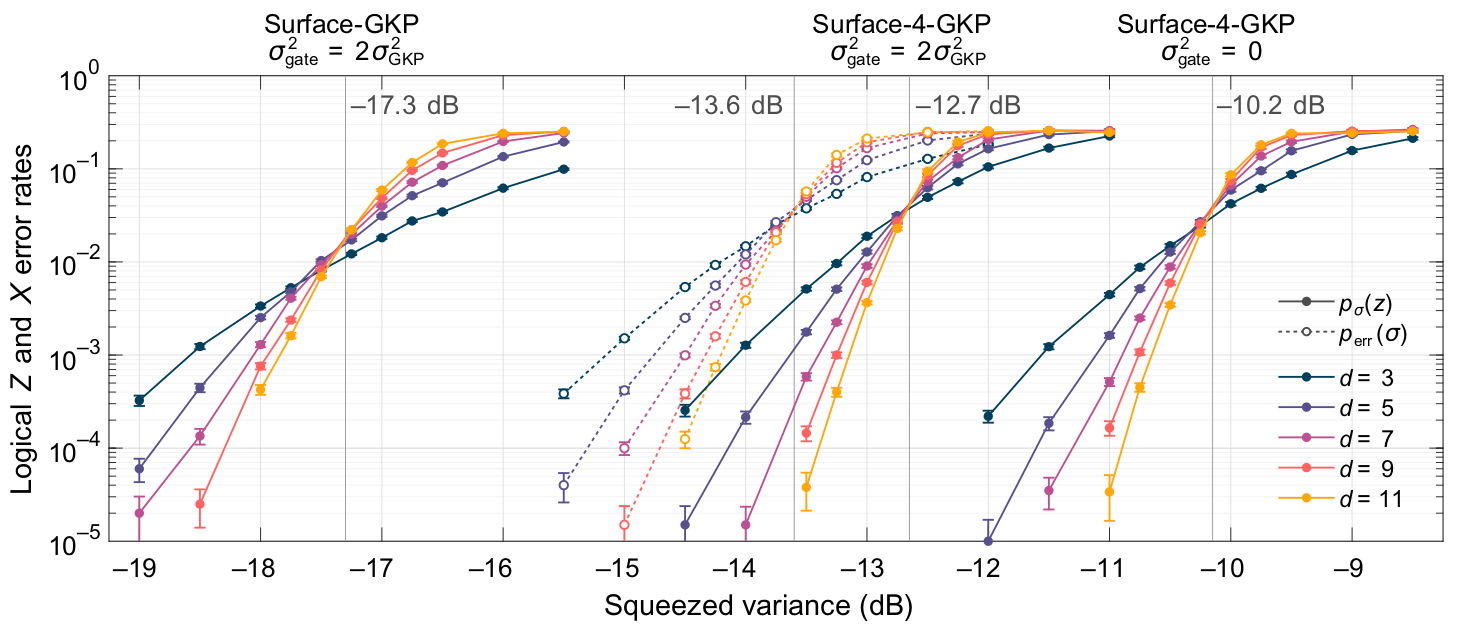
We obtain a rather good squeezing threshold of 12.7 dB

Abhinav Verma
Ulrik Andersen
Subhashish Barik
Casper Breum
Lucas Faria
Mikkel Larsen



