Quantum computing
(in the cloud)
Jonas S. Neergaard-Nielsen



QuantumDTU Summer School on Quantum Technology
15 August 2019
Slides (with some interactivity) available at
On the menu
- brief overview
- the ingredients: qubits, gates, measurements
- the dishes: circuits, algorithms
- the bad aftertaste: errors
- the other restaurants in town: NISQ, quantum players, open tools
The poster child
of quantum technology
largest hype
largest investments
largest potential value
longest time horizon
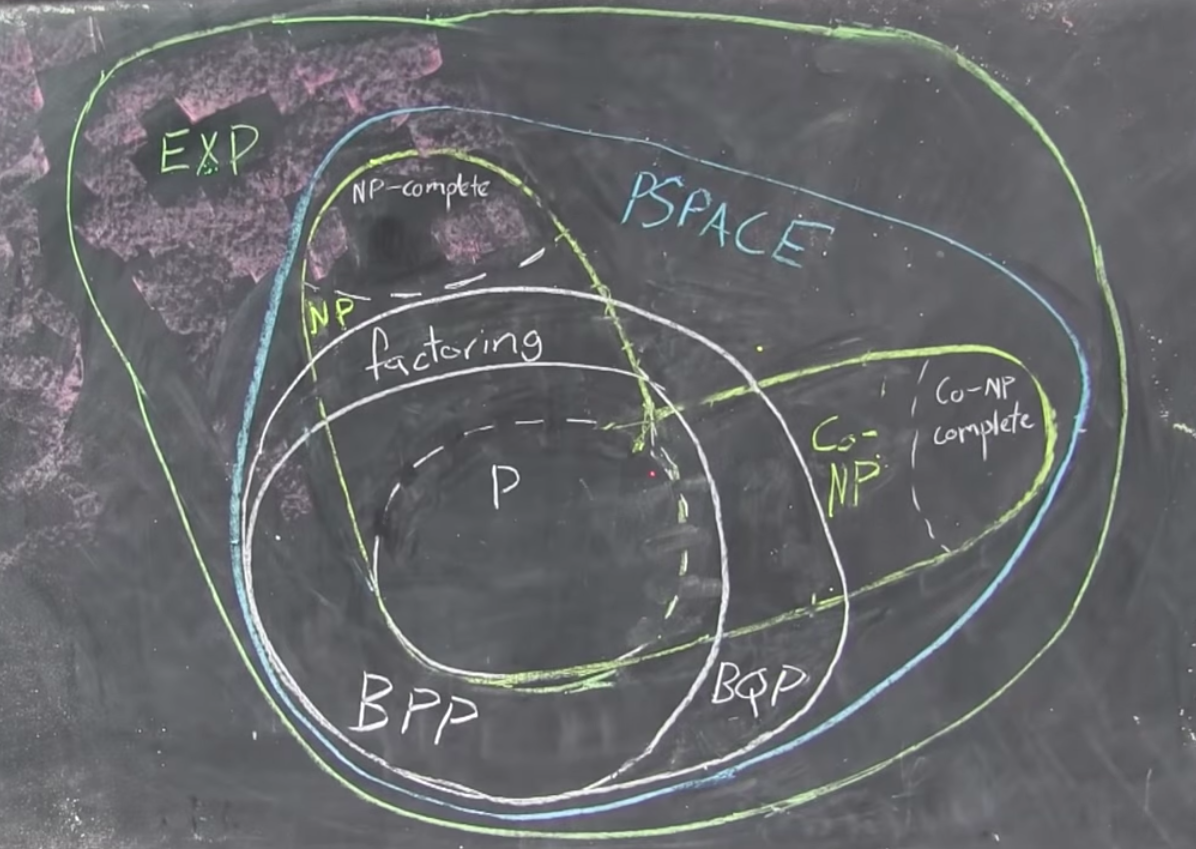
Computational complexity
Some computational problems are hard
- meaning, very VERY hard!

You do not mess with exponential scaling...
Because of superposition and entanglement, quantum systems scale exponentially in qubit size
Computational complexity
source: hackerdashery, YouTube
I love when someone can make a 10 min video that conceptually explains a CS topic better than my grossly overpaid professor that can't take the time to make decent slides.
YouTube comment
Simulating quantum

Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.
Richard Feynman
Quantum supremacy

Classical systems cannot in general simulate quantum systems efficiently.
We cannot yet prove this claim, either mathematically or experimentally, but we have reason to believe it is true; arguably, it is one of the most interesting distinctions ever made between quantum and classical.
It means that well controlled large quantum systems may “surpass understanding,” behaving in ways we find surprising and delightful.
We therefore hope to hasten the onset of the era of quantum supremacy, when we will be able to perform tasks with controlled quantum systems going beyond what can be achieved with ordinary digital computers.
John Preskill
Low-level building blocks
- initialized qubits
- 1-qubit gates
- 2- and/or 3-qubit gates
- measurements (+ possibly feed-forward)

Quantum circuits
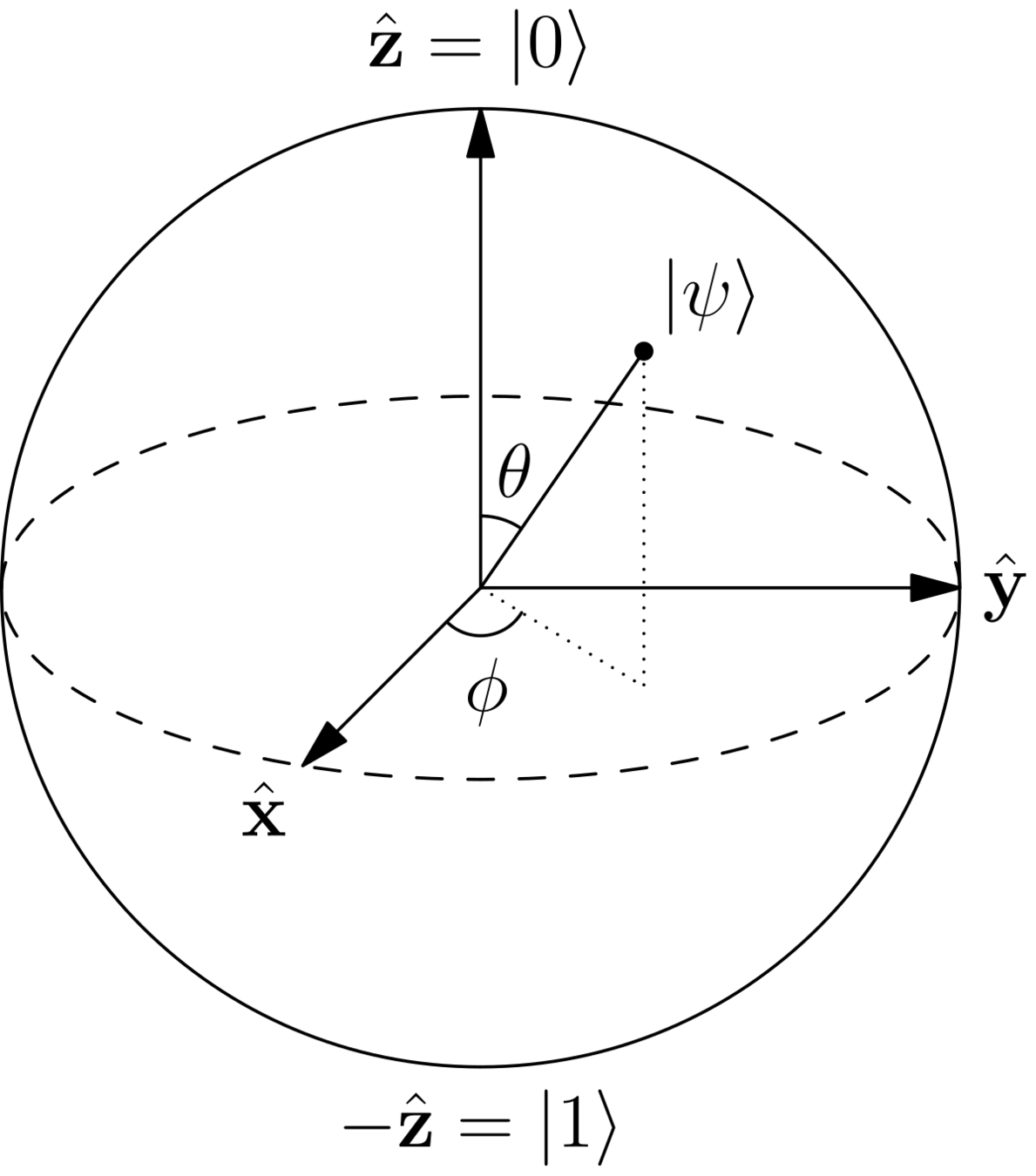
Qubits

Gates
X
Y
Z
S
T
H
X (or NOT) gate - flips the basis states
Y gate - flips around the Y-axis
Z gate - π phase shift (flip around Z)
phase gate - π/2 phase shift
π/4 gate
Hadamard gate - changes basis
$$ \frac{1}{\sqrt{2}}\!\left(\!\!\begin{array}{cc}1 & 1 \\1 & -1\end{array}\!\!\right) $$
Gates
U
SWAP gate - does what it says
CNOT - controlled-NOT (C-X)
C-U - controlled unitary
Toffoli - controlled-controlled-NOT
vectorcise!
Measurements

H
H

Z
+ feed-forward
Quantum teleportation
source: Quirk
Quantum Fourier transform
(core part of Shor's factoring algorithm)
$$ \hat{U}_{QFT} |x\rangle = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} \exp\! \left( i \frac{2\pi x k}{2^n} \right) |k\rangle $$
Algorithms
Deutsch-Jozsa
- 1992 - first algorithm to show speedup over classical
- at least over deterministic approach (P, not BPP) - illustrates some central ideas in Q.C.
- inputs in superposition
- ancilla qubits
- oracle queries
- phase kick-back
- answer by interference
- utterly useless!
Deutsch-Jozsa
task: given an unknown function \( f: \{0,1\}^n \rightarrow \{0,1\} \) which is promised to be either constant or balanced (half of function values are 0, the other half 1),
determine with certainty which it is - constant or balanced
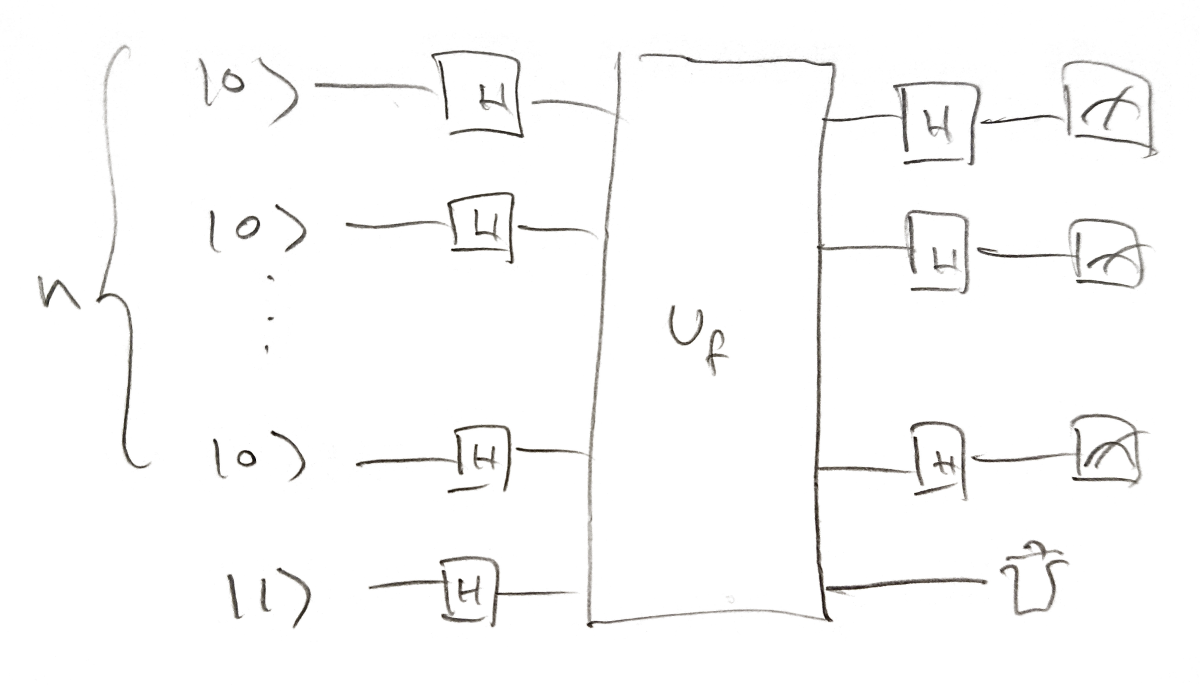
"oracle" - implements \( \hat{U}_f |x\rangle |y\rangle = |x\rangle |y \oplus f(x) \rangle \)
input \( |x\rangle \), encoding the number \( x \in [0; {2^n-1}] \)
ancilla qubit \( |y\rangle \)
Deutsch-Jozsa
whiteboard
&
quantum computer - in the cloud!

IBM Q System One

Quantum algorithm zoo
Factoring Superpolynomial
Discrete-log Superpolynomial
Pell's Equation Superpolynomial
Principal Ideal Superpolynomial
Unit Group Superpolynomial
Class Group Superpolynomial
Gauss Sums Superpolynomial
Primality Proving Polynomial
Solving Exponential Congruences Polynomial
Verifying Matrix Products Polynomial
Subset-sum Polynomial
Decoding Varies
Constraint Satisfaction Polynomial
Quantum Cryptanalysis Various
Searching Polynomial
Abelian Hidden Subgroup Superpolynomial
Non-Abelian Hidden Subgroup Superpolynomial
Deutsch-Jozsa Exponential over P, none over BPP
Formula Evaluation Polynomial
Hidden Shift Superpolynomial
Bernstein-Vazirani Polynomial Directly, Superpolynomial Recursively
Matrix Elements of Group Representations Superpolynomial
Gradients, Structured Search, and Learning Polynomials Polynomial
Polynomial interpolation Varies
Pattern matching Superpolynomial
Linear Systems Superpolynomial
Ordered Search Constant factor
Graph Properties in Adjacency Matrix Model Polynomial
Graph Properties in Adjacency List Model Polynomial
Welded Tree Superpolynomial
Collision Finding and Element Distinctness Polynomial
Graph Collision Polynomial
Matrix Commutativity Polynomial
Group Commutativity Polynomial
Hidden Nonlinear Structures Superpolynomial
Center of Radial Function Polynomial
Group Order and Membership Superpolynomial
Group Isomorphism Superpolynomial
Matrix Multiplication over Semirings Polynomial
Quantum Approximate Optimization Superpolynomial
Statistical Difference Polynomial
Finite Rings and Ideals Superpolynomial
Counterfeit Coins Polynomial
Matrix Rank Polynomial
Subset finding Polynomial
Search with Wildcards Polynomial
Network flows Polynomial
Electrical Resistance Exponential
Machine Learning Varies
Junta Testing and Group Testing Polynomial
Quantum Simulation Superpolynomial
Knot Invariants Superpolynomial
Three-manifold Invariants Superpolynomial
Partition Functions Superpolynomial
Adiabatic Algorithms Unknown
Semidefinite Programming Superpolynomial
Zeta Functions Superpolynomial
Weight Enumerators Superpolynomial
Simulated Annealing Polynomial
String Rewriting Superpolynomial
Matrix Powers Superpolynomial
source: Quantum Algorithm Zoo
Quantum error correction
Logical vs. physical qubits
Encode logical qubits in multiple physical qubits
- local errors can then be detected and corrected
these states are +1 eigenstates of the stabilizer operators \( ZZI = \hat{Z} \otimes \hat{Z} \otimes \hat{I} \) and \( IZZ = \hat{I} \otimes \hat{Z} \otimes \hat{Z} \)
If one of the 3 qubits has flipped, i.e. \( XII|\tilde\psi\rangle \), \( IXI|\tilde\psi\rangle \) or \( IIX|\tilde\psi\rangle \),
measurement of \(ZZI\) and \(IZZ\) - the error syndrome - will reveal which qubit flipped
Exercise 1: Calculate expectation values \(\langle ZZI \rangle \) and \(\langle IZZ \rangle \) for all 3 bit flips.
Exercise 2: Design a circuit that encodes the logical qubit and performs the syndrome measurement using 2 ancilla qubits
Fault-tolerant QC
Schemes with 5 or more qubits can correct arbitrary single-qubit errors
More advanced schemes with better properties exist, e.g.
- surface codes - high error thresholds around ~1%
- bosonic codes - encoding in high-dimensional harmonic oscillators
With error correction and error rates below a certain threshold, fault-tolerant quantum computing is possible, in principle
Still, ~1000 physical qubits required for one good, protected logical qubit
- many millions of physical qubits required for any reasonably useful use case
Current quantum computing landscape
Even with fault-tolerant quantum computing still a rather distant dream, we are now
entering a pivotal new era in quantum technology. [...]I needed a name to describe
this impending new era, so I made up a word: NISQ. This stands for Noisy Intermediate-
Scale Quantum.

John Preskill
NISQ
NISQ
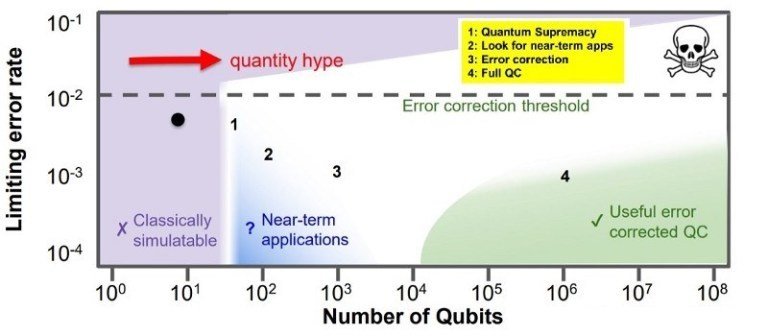
John Martinis, Google - via QWA
NISQ
- quantum simulation
- chemistry
- annealing, boson sampling
- optimization problems
- hybrid quantum-classical (e.g. VQE)
- quantum semi-definite programming
- machine learning
- and simply learning about quantum computers!
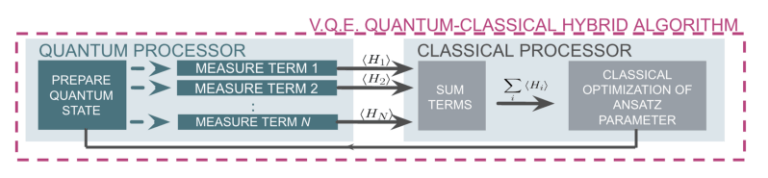
Rigetti - via QWA





Turing
Universal Quantum
Xanadu
Xofia
Zapata Computing
ZY4
Accenture
Airbus Group
Alibaba Group
Archer Exploration Limited
AT&T (INQNET Alliance)
Atos Quantum
Baidu
Booz Allen Hamilton
Google Quantum AI Lab
Honeywell
HP
IBM
Intel
JSR Corporation
Lockheed Martin
Microsoft
Mitsubishi Electric
Nokia Bell Labs
Northrup Grumman
NTT Basic Research Laboratories
Quantum Computing Inc.
Raytheon
Toshiba – Cambridge Research Laboratory
1QBit
A*Quantum
Agnostiq
Aliro Technologies
Alpine Quantum Technologies, GmbH
Ankh.1
Anyon Systems Inc.
ApexQubit
AppliedQubit
Artiste-qb.net
Atom Computing
Aurora Quantum Technologies
Automatski
BardeenQ Labs
Beit.tech
Bleximo
Boxcat
Black Brane Systems
bra-ket science
BraneCell
Cambridge Quantum Computing Ltd
Chicago Quantum
ColdQuanta
CryptoNext Security
D Slit Technologies
D-Wave Systems Inc.
Delft Circuits
EeroQ
Elyah
Entanglement Partners
Entropica Labs
Source:
evolutionQ
GTN LTD
H-Bar Consultants
Horizon Quantum Computing
HQS Quantum Simulations
Huawei
ID Quantique
InfiniQuant
IonQ
IQM Finland
ISARA
JoS QUANTUM
Ketita Labs
KETS Quantum Security
kiutra
Labber Quantum
M-Labs
Magiq
MDR
Multiverse Computing
NetraMark
NextGenQ
Nordic Quantum Computing Group
Nu Quantum
Origin Quantum Computing
Oxford Quantum Circuits
Pasqal
Phase Space Computing
PhaseCraft
Post-Quantum (PQ Solutions)
ProteinQure
PsiQuantum
Q&I
Q-Ctrl
Q-Lion
Qasky
QbitLogic
Qblox
QC Ware
QEYnet
Qilimanjaro Quantum Hub
Qindom
Qnami
Qrithm
Qrypt
Qu & Co
Quandela
Quantastica
QuantFi
QuantiCor Security
Quantika
Quantopo
Quantum Benchmark Inc.
Quantum Circuits, Inc.
Quantum Factory
Quantum Impenetrable
Quantum Machines
Quantum Motion Technologies
Quantum Phi
Quantum Thought
Quantum Xchange
QuantumCTek
QuantumX
Quantumz.io
QuBalt GmbH
Qubitekk
Qubitera, LLC
Qubit Reset LLC
QuDot
Quintessence Labs
QuiX
Qulab
QunaSys
Qunnect
QuNu Labs
QURECA
Quside
QxBranch
Rahko
Rigetti Computing
Riverlane
SeeQC.EU
SHYN
Sigma-i
Silicon Quantum Computing
softwareQ
Solid State AI
Sparrow Quantum
SpeQtral
Spin Quantum Tech
Strangeworks
Tokyo Quantum Computing
TundraSystems Global LTD
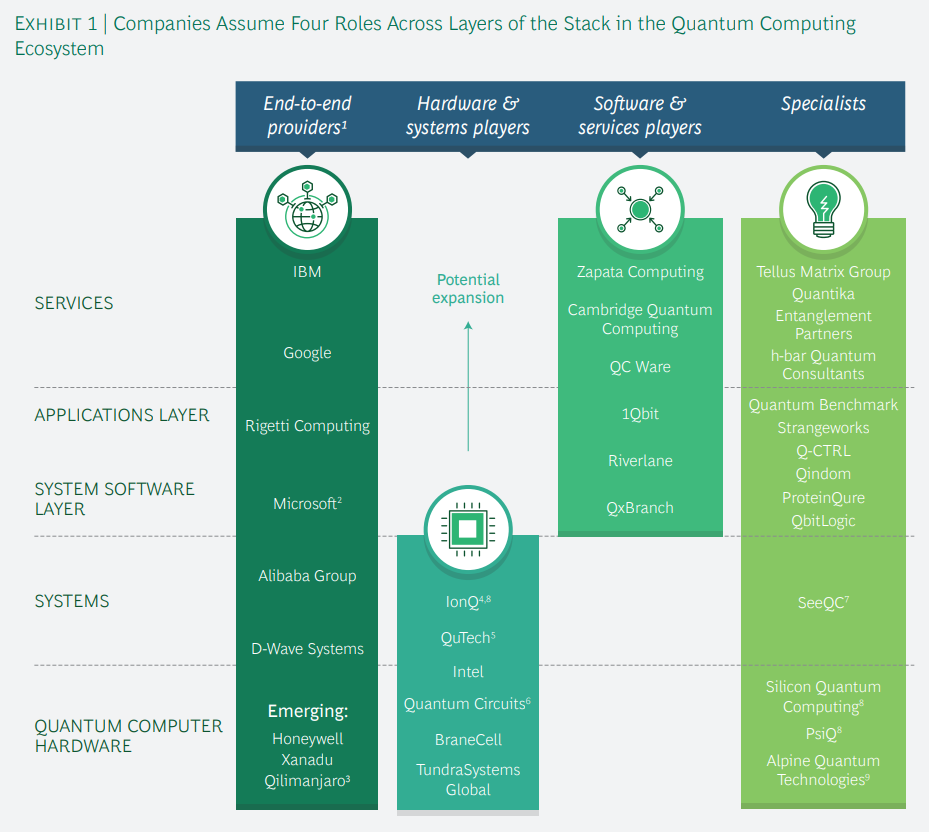
Source: Boston Consulting Group
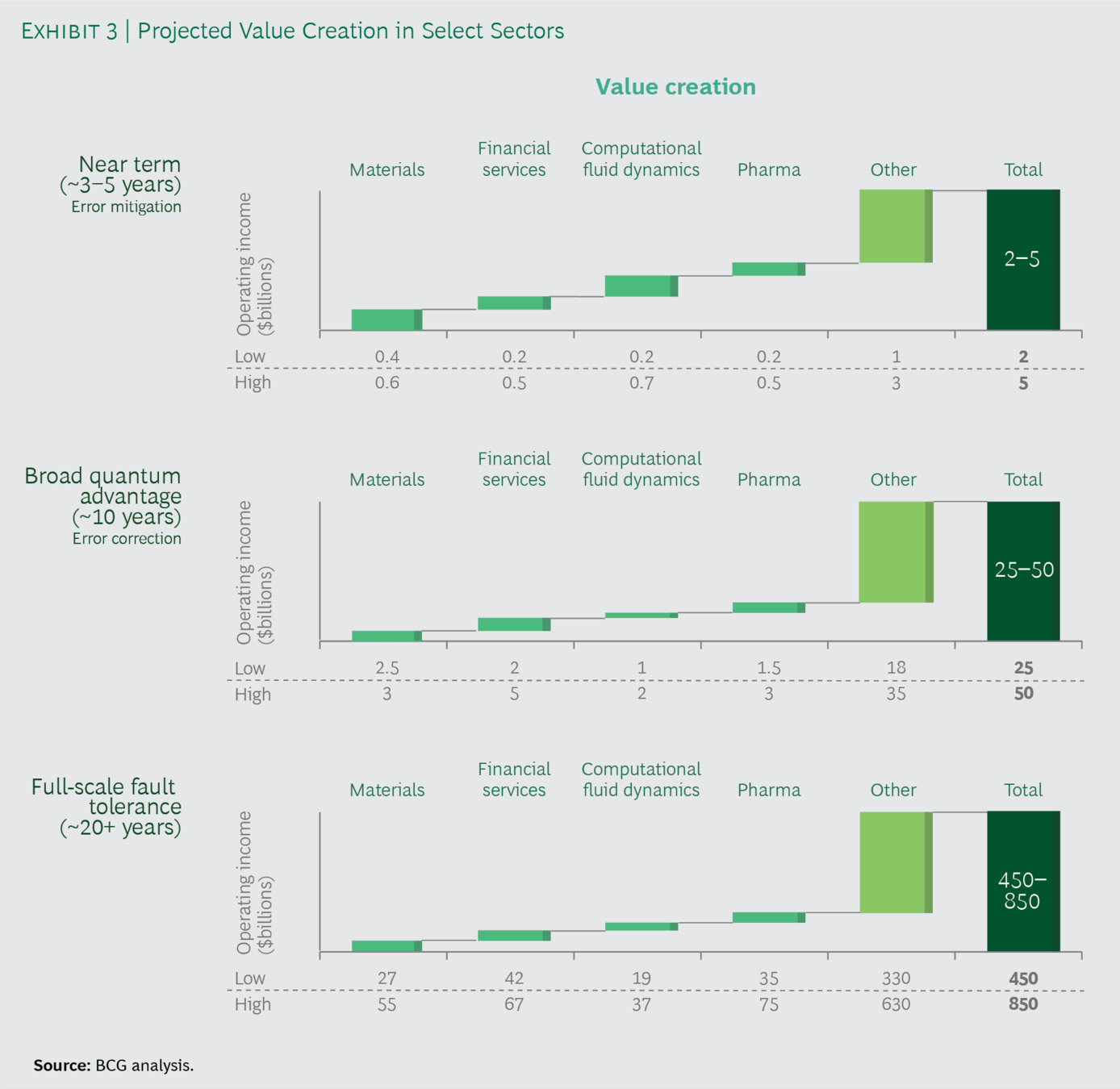
Source: Boston Consulting Group
Be aware of the hype
But - they're already very useful!

ProjectQ is an open-source software framework for quantum computing started at ETH Zurich. It allows users to implement their quantum programs in Python using a powerful and intuitive syntax. ProjectQ can then translate these programs to any type of back-end, be it a simulator run on a classical computer or an actual quantum chip.
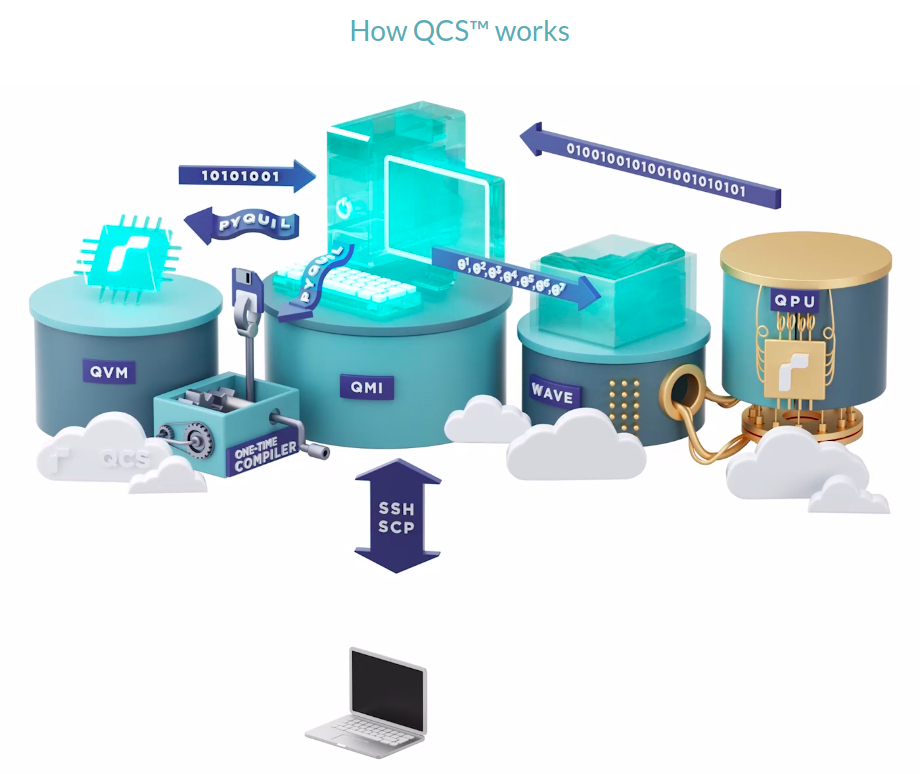



many other available tools...