Conflict-driven cutting-plane learning
The devil is in the details

Jo Devriendt
jodevriendt.com
 


Acknowledgment:

MIAO group at Lund/Copenhagen

 


slides: slides.com/jod/cdcpl-devil

How to solve?
"Generate-and-test" search tree...
...maybe we get lucky with good heuristics?

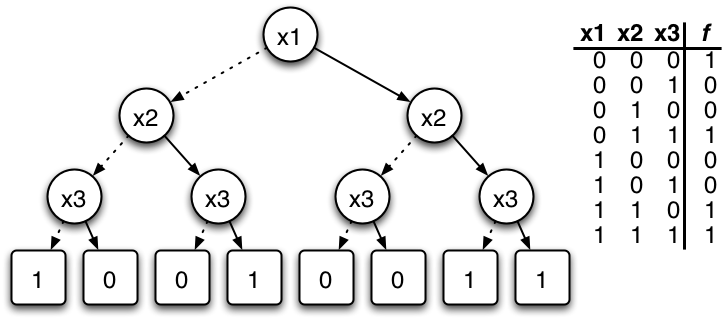
  • variables
  • values
  • find a variable-value assignment that satisfies a number of constraints

Combinatorial search

Combinatorial search

Suppose the problem is UNSATisfiable:

  • heuristics don't help
  • strong pruning (propagation) helps, but often kicks in only after deciding on many variables

How to derive that no candidate solution satisfies all constraints?

Proof construction

x + y - z \geq 1 \\ w - y + z \geq 1 \\ -x -w \geq -1 \\

To show UNSAT of above constraints,
just add all of them together.

0 \geq 1

No need to search over candidate solutions!

Dual reasoning

besides searching over variable-value assignments,
search over constraint combinations

Preliminaries

  • Boolean variables: take value \(0\) or \(1\)
  • Negated variables: $$\overline{x}=1-x \text{ or } \overline{x}+x=1$$
    • variable or its negation is a literal
  • Linear inequalities (positive coefficients): $$x+2\overline{y}+3z \geq 4$$
  • Propositional clause: $$x \vee \overline{y} \vee z$$ is equivalent to $$x+\overline{y}+z \geq 1$$
x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\

\(z\)

\(\overline{z}\)

Naive SAT solver

  • Depth-first search
  • Unit propagation:
    propagate single non-falsified literal in clause

\(x\)

\(y\)

\(\overline{y}\)

\(\overline{z}\)

\(z\)

x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\

Naive SAT solver

  • Depth-first search
  • Unit propagation:
    propagate single non-falsified literal in clause

\(x\)

\(y\)

\(z\)

\(\overline{z}\)

\(\overline{x}\)

\(y\)

\(\overline{y}\)

x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\

Naive SAT solver

  • Depth-first search
  • Unit propagation:
    propagate single non-falsified literal in clause

\(\overline{y}\)

\(\overline{z}\)

\(z\)

\(x\)

\(y\)

\(z\)

\(\overline{z}\)

x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\

Preliminaries

Decision literals

Search trail: the current assignment, as a list of literals in chronological order, paired with their decision status

Reason constraint

d d p
\overline{y}
\overline{z}
x

Conflict constraint

Propagated literal

\(\overline{x}\)

\(y\)

\(\overline{y}\)

\(\overline{y}\)

\(\overline{z}\)

\(z\)

\(x\)

\(y\)

\(z\)

\(\overline{z}\)

Conflict-driven clause learning

  • Depth-first search
  • Unit propagation:
    propagate last non-falsified variable in clause
  • Clause learning:
  1. from each conflict, get the conflict clause
  2. iterate backwards over the trail
  3. add the reason to the conflict
  4. stop when the conflict clause propagates at a previous decision point, add the current conflict as a learned clause
  5. backtrack to the propagating decision point, continue search

Conflict-driven clause learning

\(x\)

\(y\)

\(z\)

\(\overline{z}\)

\textcolor{red}{\overline{y}\geq 1}
x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\
z
p
y
d
x
d
  1. from each conflict, get the conflict clause
  2. iterate backwards over the trail
  3. add the reason to the conflict
  4. stop when the conflict clause propagates at a previous decision point, add the current conflict as a learned clause
  5. backtrack to the propagating decision point, continue search

\(\overline{y}\)

\(\overline{z}\)

\(x\)

\(\overline{x}\)

\overline{y} \geq 1
y \geq 1
y + z \geq 1
0 \geq 1

Conflict-driven clause learning

x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\
x
p
\overline{z}
p
\overline{y}
p
  1. from each conflict, get the conflict clause
  2. iterate backwards over the trail
  3. add the reason to the conflict
  4. stop when the conflict clause propagates at a previous decision point, add the current conflict as a learned clause
  5. backtrack to the propagating decision point, continue search

Crucial invariants

  • addition eliminates propagated literal from conflict
  • at every step, conflict is falsified by trail
    (contains only false literals)
\frac{z+X+W\geq 1 ~~~~~ \overline{z}+ Y +W \geq 1}{X+Y+W \geq 1}
\frac{z+\overline{x} \geq 1 ~~~~~ \overline{z}+ y \geq 1}{\overline{x}+y\geq 1}

"add" the clauses

\frac{z+\overline{x}+\textcolor{red}{w} \geq 1 ~~~~~ \overline{z}+ y+\textcolor{red}{w} \geq 1}{\overline{x}+y+\textcolor{red}{2}w\geq 1}
\frac{}{\lceil\frac{\overline{x}+y+2w}{2}\rceil\geq \lceil\frac{1}{2}\rceil}
\frac{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}{\overline{x}+y+\textcolor{red}{w}\geq 1}

Resolution rule

In case of double literals:

Divide lhs and rhs by 2, ceil:

\(\overline{y}\)

\(\overline{z}\)

\(x\)

\(\overline{x}\)

\overline{y} \geq 1
y \geq 1
y + z \geq 1
0 \geq 1

Conflict-driven clause learning

x + y + z \geq 1\\ \overline{x} + y + z \geq 1\\ y + \overline{z} \geq 1 \\ \overline{y} + z\geq 1 \\ \overline{y} + \overline{z}\geq 1 \\
x
p
\overline{z}
p
\overline{y}
p
  • every "addition" is an application of resolution rule
  • all learned clauses form a resolution proof

Automatic proof construction (dual reasoning) during search!

Conflict-driven clause learning

Crucial invariants

  • addition eliminates propagated literal from conflict
  • at every step, conflict is falsified by trail

Mid-presentation summary

  • from search conflicts, derive constraints
  • apply resolution rule to conflict clause and reason clauses
  • build resolution proofs

Can we do better?

  • Resolution is not only proof system
  • Field of proof complexity
    • given an unsatisfiable formula, what is the shortest proof possible?
  • Resolution is the weakest of all proof systems!
    • there exist simple formulas where smallest resolution proof is exponential [H85]
    • other proof systems are polynomial
    • lower bound to solve time!
  • E.g., cutting plane (CP) proof system

Cutting plane proofs

Rules:

  • Boolean axiom

     
  • Addition

     
  • Multiplication

     
  • Division

     
  • Trivial inconsistency:
\frac{}{x \geq 0} \;\;\;\; \frac{}{\overline{x} \geq 0}
\frac{ \sum_i a_i x_i \geq b \;\;\;\; c \in \mathbb{N}^+ } { \sum_i ca_i x_i \geq cb }
\frac{ \sum_i a_i x_i \geq b \;\;\;\; \sum_i c_i x_i \geq d } { \sum_i (a_i+c_i) x_i \geq b+d }
\frac{ \sum_i a_i x_i \geq b \;\;\;\; c \in \mathbb{N}^+ } { \sum_i \lceil\frac{a_i}{c}\rceil x_i \geq \lceil \frac{b}{c} \rceil }
0 \geq 1

Can simulate resolution rule

Conflict-driven cutting-plane learning

Can we construct cutting plane proof during search, similar to resolution via CDCL?

  • add reason constraints to conflict constraint
  • eliminating propagated variables
  • keeping constraint falsified by trail
  • add learned constraint to continue search

Let's see...

  • Input: 0-1 linear constraints
  • Depth-first search
    •  with decisions and propagated literals as a trail

Conflict-driven cutting-plane learning

d d d
\overline{y}
v
\overline{x}
2\overline{y}+2z+\overline{v} \geq 3\\

Slack

Given a trail, the slack of the constraint is the difference between the lhs and the rhs (assuming unknown literals as true)

\textcolor{red}{2}+2z+\textcolor{red}{0} \geq 3\\

slack =
2+2+0-3 =
1

  • slack<0 means constraint is conflicting
  • all unknown literals with coefficient greater than slack propagate to true

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\

Problem

\textcolor{red}{2}\\ \textcolor{red}{2}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\

Problem

\textcolor{red}{1}\\ \textcolor{red}{1}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d
z
p

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\

Problem

\textcolor{red}{1}\\ \textcolor{red}{-1}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d
z
p
  • add reason constraint to conflict
  • use division/multiplication to eliminate propagated literal
  • keep constraint conflicting (slack<0)
w+x+2y \geq 2\\
\textcolor{red}{0}\\

Slack is sub-additive: slack of summed constraints is at most sum of slacks

Can we get the reason constraint to slack 0 with the coefficient of the propagated variable identical to the conflict coefficient?

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\

round-to-one [NE18]

\textcolor{red}{1}\\ \textcolor{red}{-1}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d
z
p
  • adding variable axioms \(x \geq 0\) for falsified literal \(x\) does not change slack
  • adding variable axioms \(\overline{x} \geq 0\) for non-falsified literal \(x\) does not change slack
  • dividing by a common divisor \(d\) of all coefficients yields \(\lfloor\frac{slack}{d}\rfloor\)
  • slack is always lower than propagating coefficient

Divide by propagating coefficient, after ensuring all coefficients are divisible

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\

round-to-one [NE18]

\textcolor{red}{1}\\ \textcolor{red}{-1}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d
z
p

Divide by propagating coefficient, after ensuring all coefficients are divisible

1) non-falsified: add \(\overline{x}\geq 0\)

2) falsified: add \(y \geq 0\)

divisor

2y+2z \geq 1\\
y+z \geq 1\\

3) divide by 2

4) multiply with conflict coefficient

2y+2z \geq 2\\

5) add to conflict

w+3y \geq 2\\
\textcolor{red}{-1!}\\
\textcolor{red}{1}\\
\textcolor{red}{0}\\
\textcolor{red}{0}\\

Conflict-driven cutting-plane learning

x+y+2z \geq 2\\ w+y+2\overline{z} \geq 2\\
\textcolor{red}{1}\\ \textcolor{red}{-1}\\

constraints

slack

trail

x
d
w
d
\overline{y}
d
z
p

1) non-falsified: add \(\overline{x}\geq 0\)

2) falsified: add \(y \geq 0\)

divisor

2y+2z \geq 1\\
y+z \geq 1\\

3) divide by 2

4) multiply with conflict coefficient

2y+2z \geq 2\\

5) add to conflict

w+3y \geq 2\\
\frac{}{x \geq 0} \;\;\;\; \frac{}{\overline{x} \geq 0}
\frac{ \sum_i a_i x_i \geq b \;\;\;\; c \in \mathbb{N}^+ } { \sum_i ca_i x_i \geq cb }
\frac{ \sum_i a_i x_i \geq b \;\;\;\; \sum_i c_i x_i \geq d } { \sum_i (a_i+c_i) x_i \geq b+d }
\frac{ \sum_i a_i x_i \geq b \;\;\;\; c \in \mathbb{N}^+ } { \sum_i \lceil\frac{a_i}{c}\rceil x_i \geq \lceil \frac{b}{c} \rceil }

Building cutting plane proofs!

\textcolor{red}{-1!}\\
\textcolor{red}{1}\\
\textcolor{red}{0}\\
\textcolor{red}{0}\\

Conflict-driven cutting-plane learning

round-to-one [NE18]

Divide by propagating coefficient, after ensuring all coefficients are divisible, then multiply by conflict coefficient.

Rest of search routine: roughly same as CDCL

Efficient implementation: gitlab.com/JoD/exact

Applications

  • Find unsatisfiability
    • prove optimality of solution
    • find intersection of all solutions
    • prove logical consequence
  • Currently used to generate explanations for constraint programs with CPMpy (faster than Google OR-tools)
  • Used as backend solver for IDP-like system
  • Verification of bit-level multiplier circuits [LBDEN20]
  • Formal verification of clausal decomposition of constraints with VeriPB
  • Can perform well when linear relaxation of problem is bad - improved a MIPLIB instance

What now?

Round-to-one is not the final answer

  • Divisors different from propagating coefficient?
    • yes, all divisors greater than slack should work
  • How many axioms to add?
    • [EN18] adds maximal amount, but rather as little as needed?
  • Manipulate conflict instead of propagating constraint?
    • definitely possible!
  • Other sensible ways of transforming constraint?
    • yes, e.g., saturation rule and mixed-integer-rounding cut

strictly stronger than regular division!

Way more degrees of freedom than in CDCL ...

... thesis topic :)

What does Exact do?

Efficient implementation: gitlab.com/JoD/exact

  1. Multiply reason constraint with conflict coefficient
  2. If propagating coefficient suffices as divisor, use that
  3. Else, try to find multiple of propagating coefficient that yields a divisor of conflict coefficient
  4. Else, round to one
  5. Use axiom addition sparingly
  6. Except when reducing small coefficients as long as \(\lceil\frac{rhs}{divisor}\rceil\) remains unchanged.

Thanks for listening!

Questions?

[H85] The intractibility of resolution - Haken

[CCT87] On the complexity of cutting-plane proofs - Cook, Coullard, Turán

[MS96] GRASP - a new search algorithm for satisfiability - Marques-Silva, Sakallah

[BS97] Using CSP lookback techniques to solve real-world SAT instances - Bayardo, Schrag

[MMZZM01] Chaff: Engineering an efficient SAT solver - Moskewicz, Madigan, Zhao, Zhang, Malik

[CK05] A fast pseudo-Boolean constraint solver - Chai, Kuehlmann

[SS06] Pueblo: A hybrid pseudo-Boolean SAT solver - Sheini, Sakallah

[LP10] The Sat4j library, release 2.2 - Le Berre, Parrain

[EN18] Divide and conquer: Towards faster pseudo-boolean solving - Elffers, Nordström

[D20] Watched Propagation for 0-1 Integer Linear Constraints - Devriendt

[DGN20] Learn to Relax: Integrating 0-1 Integer Linear Programming with Pseudo-Boolean Conflict-Driven Search - Devriendt, Gleixner, Nordström

[SDNS20] Theoretical and Experimental Results for Planning with Learned Binarized NeuralNetwork Transition Models - Say, Devriendt, Nordström, Stuckey

[LBDEN20] Verifying Properties of Bit-vector Multiplication Using Cutting Planes Reasoning - Liew, Beame, Devriendt, Elffers, Nordström

RoundingSat

[LBDEN20]

  • Verification of various bit-level multiplier circuits
  • All instances are unsatisfiable