11b. Quicksort
2021-03-14
slides.com/jod/pt_11b
Docent: Jo Devriendt
Assistent: Ann Philips
Coördinator: Joost Vennekens
voornaam.achternaam@kuleuven.be

Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Quicksort
Centraal idee:
- kies een element, de pivot
- zet alles kleiner er links van
- zet alles groter (of gelijk) er rechts van
- pivot staat nu goed
- sorteer de linkse en rechtse elementen recursief
Verdeel en heers-algoritme
Splits probleem op in deelproblemen, oplossing van globale probleem steunt op oplossing deelproblemen
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
5 3 1 7 2 6 4 5
3 1 2 4 5 5 7 6
5 3 1 7 2 6 4 5
3 1 2 455 7 6
3 1 2 455 6 7
3 1 245567
1 2 345567
12345567
12345567
Legende:
- nieuwe pivot
- linker- en rechterkant
oude pivot
1 2 3 4 5 5 6 7
Noot: we nemen altijd het laatste element uit de te sorteren elementen als pivot
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Quicksort gevisualiseerd
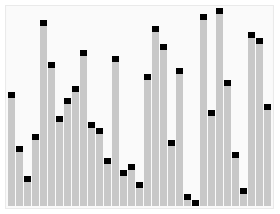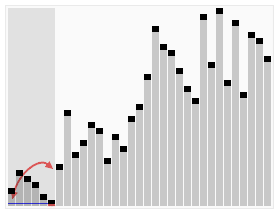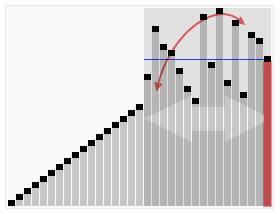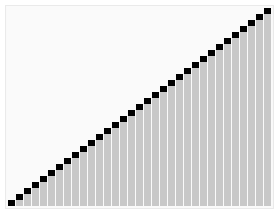
https://commons.wikimedia.org/wiki/File:Sorting_quicksort_anim.gif
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Code
int partition(int a[], int lo, int hi);
void quick(int a[], int lo, int hi);- lo en hi geven beginindex en eindindex van de huidige subarray - a[lo..hi+1]
- partition kiest een pivot, zet alle kleinere elementen links, de pivot ernaast, en geeft de index van de pivot terug
- quick verzorgt het recursieve deel
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Code
int partition(int a[], int lo, int hi) {
int pivot = a[hi];
int pivotIdx = lo;
for (int j = lo; j < hi; ++j) {
if (a[j] < pivot) {
swap(&a[pivotIdx], &a[j]);
++pivotIdx;
}
}
swap(&a[pivotIdx], &a[hi]);
return pivotIdx;
}Zet kleinere elementen links
pivot is laatste element
Zet pivot vlak na de kleinere elementen
pivotIdx zal uiteindelijk index van pivot bevatten
void quick(int a[], int lo, int hi) {
if (hi <= lo) {
return;
}
int pivotIdx = partition(a, lo, hi);
quick(a, lo, pivotIdx - 1);
quick(a, pivotIdx + 1, hi);
}Triviaal geval
Kies pivot, verdeel in links en rechts stuk
Sorteer links en rechts stuk
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Code
#define N 8
int main() {
int a[N] = {5,3,1,7,2,6,4,5};
quick(a, 0, N - 1);
for (int i = 0; i < N; ++i) {
printf("%d ", a[i]);
}
printf("\n");
}$ ./a.out
1 2 3 4 5 5 6 7Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Analyse
5 3 1 7 2 6 4 5
3 1 2 4 5 5 7 6
5 3 1 7 2 6 4 5
3 1 2 455 7 6
3 1 2 455 6 7
3 1 245567
1 2 345567
12345567
12345567
1 2 3 4 5 5 6 7
- n = #elementen
- Iedere recursieve stap creëert twee deelproblemen
- Indien de deelproblemen altijd +- half zo groot zijn als het huidig probleem, gaat de recursie +- stappen diep
- Op elk recursieniveau doen we dan +- n stappen werk om, gesommeerd over alle subproblemen, de elementen te overlopen en naar links te verplaatsen
- Total aantal operaties is
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Zijn de deelproblemen altijd +- half zo groot?
- Als de elementen al geordend zijn, is de pivot altijd het grootste (meest rechtse) element, en is het deelprobleem gewoon alle andere elementen
- Bvb. [1,2,3,4,5,5,6,7] wordt [1,2,3,4,5,5,6],7
- Als veel elementen hetzelfde zijn, bekom je uiteindelijk een subprobleem met enkel die elementen, en is het deelprobleem telkens maar één element kleiner
- Bvb. [5,2,5,2,5,2,5,3] wordt [2,2,2],3,[5,5,5,5] en die wordt 2,[2,2],3,5,[5,5,5] enzovoort
- In zo'n gevallen heeft quicksort O(n^2) operaties nodig
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Samenvatting
- Quicksort is een verdeel en heers-algoritme dat recursief sorteert
- Het heeft meestal stappen nodig
- Maar als je pech hebt is het O(n^2)