17a. Turingmachines
2021-04-23
slides.com/jod/pt_17a
Docent: Jo Devriendt
Assistent: Ann Philips
Coördinator: Joost Vennekens
voornaam.achternaam@kuleuven.be

Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Wat is een computerprogramma?
Niet volledig akkoord: er bestaan computerprogramma's die geen uitvoerbare instructies bevatten (zie volgende lesvideo).
Wikipedia:
A computer program is a collection of instructions that can be executed by a computer to perform a specific task.
Eigen definitie:
Een computerprogramma is een beschrijving van een functie die een computer kan (proberen te) berekenen
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Wat is een functie?
Met andere woorden: een functie is een input-outputrelatie, waarbij voor elke input exact één output bestaat.
Wikipedia:
In mathematics, a function is a binary relation between two sets that associates to each element of the first set exactly one element of the second set.
Real-life voorbeeld: de functie die elk persoon afbeeldt op haar leeftijd
Abstract voorbeeld: de functie met als input alle mogelijke C-programma's en inputs voor C-programma's, en als output of het gegeven C-programma termineert op de gegeven input
Klassiek wiskundig voorbeeld:
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Wat is een computerprogramma?
Eigen definitie:
Een computerprogramma is een beschrijving van een functie die een computer kan (proberen te) berekenen
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Theoretische basis: Turingmachine (TM)
-
Wiskundig concept
- Alan Turing, 1936
- Formaliseert een berekeningsproces voor een functie f
- Model voor hoe computers werken
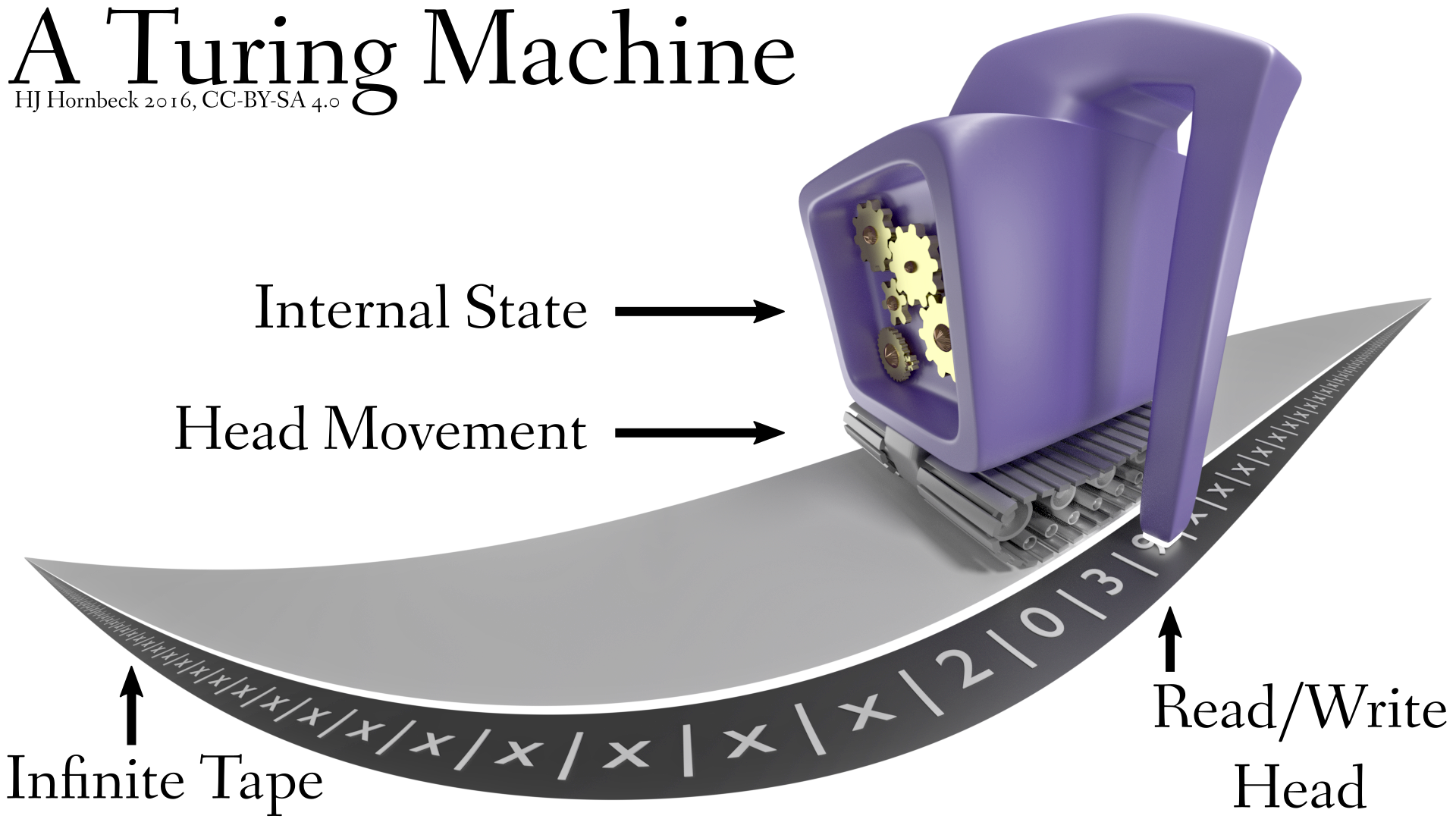
Bestaat uit
- Oneindige band waarop tekens staan geschreven
- initieel de (gecodeerde) input voor f
- uiteindelijk de (gecodeerde) output f
- Leeskop die op een teken op de band staat, die inleest, overschrijft, en een teken naar links of rechts beweegt
- Interne toestand die verandert naargelang het ingelezen teken
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Wiskundige definitie:
tupel van 7 elementen
- Verzameling toestanden
- initiële toestand
- accepterende toestanden
- Transitiefunctie
In: huidige toestand en ingelezen teken
Uit: nieuwe toestand, nieuw teken om op de band te schrijven, of de leeskop naar links of rechts moet
Turingmachine (TM)
Als een TM een processor is, dan zijn de tekens de bits, de band het geheugen, en de transitiefunctie de configuratie van logische poorten
- Verzameling tekens
- speciaal blanco teken
- inputtekens
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Turingmachine (TM)
- Laat toe om functies te berekenen:
- codeer input van functie op de band
- kies de juiste transitiefunctie
- laat de TM lopen
- op het einde staat output op de band
- In filmpje: berekening van binair increment
- Cruciaal: een functie wordt enkel berekend door een TM als voor alle inputs het juiste resultaat in eindige tijd wordt berekend
Interessante functie: "simuleer"
- In: (encodering van een) TM met input ervoor
- Out: het resultaat van het draaien van die TM op z'n input
Bestaat er een TM die "simuleer" kan berekenen?
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Universele Turingmachine (UTM)
Bestaat er een TM die "simuleer" kan berekenen?
Ja!
- Meer dan één
- Krijgt de naam Universele Turingmachine (UTM)
- Heeft slechts twee tekens en 15 toestanden nodig
- alles is binair geëncodeerd
Als een UTM een processor is, dan is de geëncodeerde TM die gesimuleerd wordt het programma
TMs kun je gebruiken om de berekeningen mee te modelleren, onafhankelijk of de berekening uitgevoerd wordt door software of hardware
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Onberekenbare functie
Kunnen alle functies door een TM uitgerekend worden?
-
Halting problem / stopprobleem
- In: geëncodeerde TM + input
- Uit: "1" als de TM ooit stopt op de input, "0" indien niet
- Merk op: simuleren van TM lukt niet, want als TM nooit stopt, ga je nooit "0" kunnen wegschrijven
- Analoog: of een willekeurig C-programma stopt voor een willekeurige input is onberekenbaar
Neen!

Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Sterkere berekeningsprocessen?
Bestaat er een berekeningsproces die een TM-onberekenbare functie kan berekenen?
Euh...
Church-Turinghypothese:
Elke functie die berekend kan worden,
kan berekend worden door een TM.
- Stopprobleem is echt wel onberekenbaar
- Sneller / efficiënter dan een TM kan wel
Argument: alle andere krachtige berekeningsprocessen tot nu toe (bvb. lambda calculus of quantum computing) kunnen niets meer dan TMs
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Turingcompleetheid
Een "systeem" is Turingcompleet indien het alle functies kan berekenen die een TM kan berekenen
- Toon aan dat je systeem elke mogelijke TM kan simuleren
- TM is een 7-tupel van tekens, toestanden en transitiefunctie
- niks meer, niks minder
- met "voldoende grote" band ipv oneindig
- TM is een 7-tupel van tekens, toestanden en transitiefunctie
- C is Turingcompleet
- Minecraft is Turingcompleet
Hoe Turingcompleetheid bewijzen?
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Turingcompleetheid
Uit de Church-Turinghypothese volgt:
elk systeem dat Turingcompleet is kan elke berekenbare functie berekenen
- Algemene programmeertalen zijn meestal Turingcompleet
-
Reguliere expressies zijn niet Turingcompleet
- "regex" pattern matching berekent of string een patroon bevat
- bvb. berekenen of een string eindigt op een 'a' kan met de regex ".*a"
- berekenen of in een string elke '(' correct afgesloten wordt met met ')' kan niet met een (standaard) regex (maar natuurlijk wel met een C-programma of TM)
Programmeertechnieken [B-KUL-YI0855]
De Nayer, IIW, E-ICT, 2Ba + schakel, 2020-2021
Samenvatting
- Een programma berekent functies
- Turingmachines vormen de wiskundige basis voor computers en programma's
- Niet alle functies kunnen berekend worden door TMs
- Bvb. het stopprobleem / halting problem
- Onder de Church-Turinghypothese zijn er geen sterkere berekeningstechnieken dan TMs
- Een systeem is Turingcompleet indien het alles kan berekenen wat een TM kan berekenen
- C is Turingcompleet
