To what extent does the volume of gas in a bottle change with changes in temperature ?
Background
Pressure
Volume
number of moles
universal gas constant
Temperature
- The universal gas law states that:
Charles law:
Since V and T vary directly, we can equate them by making use of a constant k.
Real-life applications of gas laws
PHYSICS
BIOLOGY
CHEMISTRY
Firing a bullet:
Gay Lussac’s law can be applied in firing a bullet. Here, the ignition of gunpowder generates a superheated gas which in turn increases the pressure so that the bullet travels longer with high speed.
Pressure:
Boyle's Law can be used to explain how deep sea creatures survive at low depths. Fish have no air bubbles in their blood stream so there is no space for them to be compressed. Humans have a lot of empty space as well as small air bubbles in their blood stream, so low pressure would crush them.
Hot air ballon:
Charles' Law can be applied with a hot air ballon. When the temperature increases the gas molecules move faster causing them to collide. If it's flexible, like a ballon, the pressure will stay the same. This causes the gas to increase in volume.
Hypothesis
Theory predicts that the relationship between temperature and volume is directly proportional, when pressure is held constant, and thus yield a linear graph. We are expecting to find that the theory holds for our experiment as well.
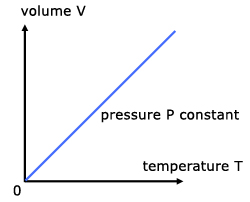
Experiment
- A straw was fixed inside the bottle cap with instant glue to ensure that the pressure inside the bottle remains constant, this was repeated for all 4 bottles
- The bottles were closed and cooled down until they reached the desired temperature ( this was measured using a thermometer )
- The bottles were then held into a beaker of water for 10 seconds each and then taken out
- The water now inside the bottles was poured into a new beaker and measured, this was repeated for all 4 bottles
- Lately, the volume of the water was calculated and subtracted from the total volume of gas previously in the bottle, this was repeated for all 4 bottles
Variables
dependent variable:
fixed variables:
- Room temperature
- Pressure
- Volume of bottle
- Volume
- Temperature
independent variable:
- Type of bottle
- Width of straw
Experiment set-up

straw
bottle
glass of water
beaker
super glue
duster spray
thermometer
Results

uncertainty in measurement of volume: ± 10cc
line of best fit

Results
From the line of best fit we can now calculate the constant k that, according to Charles law, will hold for our experiment
Conclusion
As we had expected we found the relationship between the volume of the gas inside the bottle and the temperature to be linear. That is, as temperature increased so did the volume of the gas inside the bottle. The extent to which this relationship holds is equal to the constant 22,9.