Equiangular Tight Frames

John Jasper

South Dakota State University

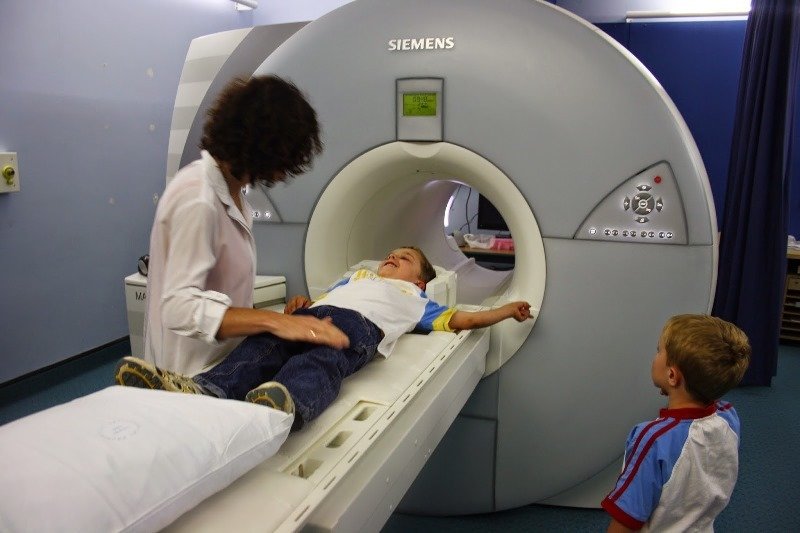
MRI: Resolution v. Scan Time

Pixels

Time

High resolution \(\Longleftrightarrow\) Long scan time

Real world signals are sparse.

\(\Downarrow\)

The conventional tradeoff is a lie!

We can solve "underdetermined"

\[Ax=b\] by \(L^{1}\) minimization provided:

\(x\) is sparse, and
Columns of \(A\) are "spread out"

Pixels

Time

Compressed Sensing

We need an image with many pixels:

\(=\)

Image

Transformed Image

A measurement is a single dot product
Using old linear algebra we need as many dot products as pixels
Under an invertible transformation the image is sparse (lots of zeros)

Compressed Sensing

We need an image with many pixels:

\(=\)

Transformed Image

Column vectors need to be "spread out" in space

For sparse signals we need a lot fewer measurements
But the columns of our sensing matrix must be "spread out" in space

Roadmap for this talk

Compressed Sensing

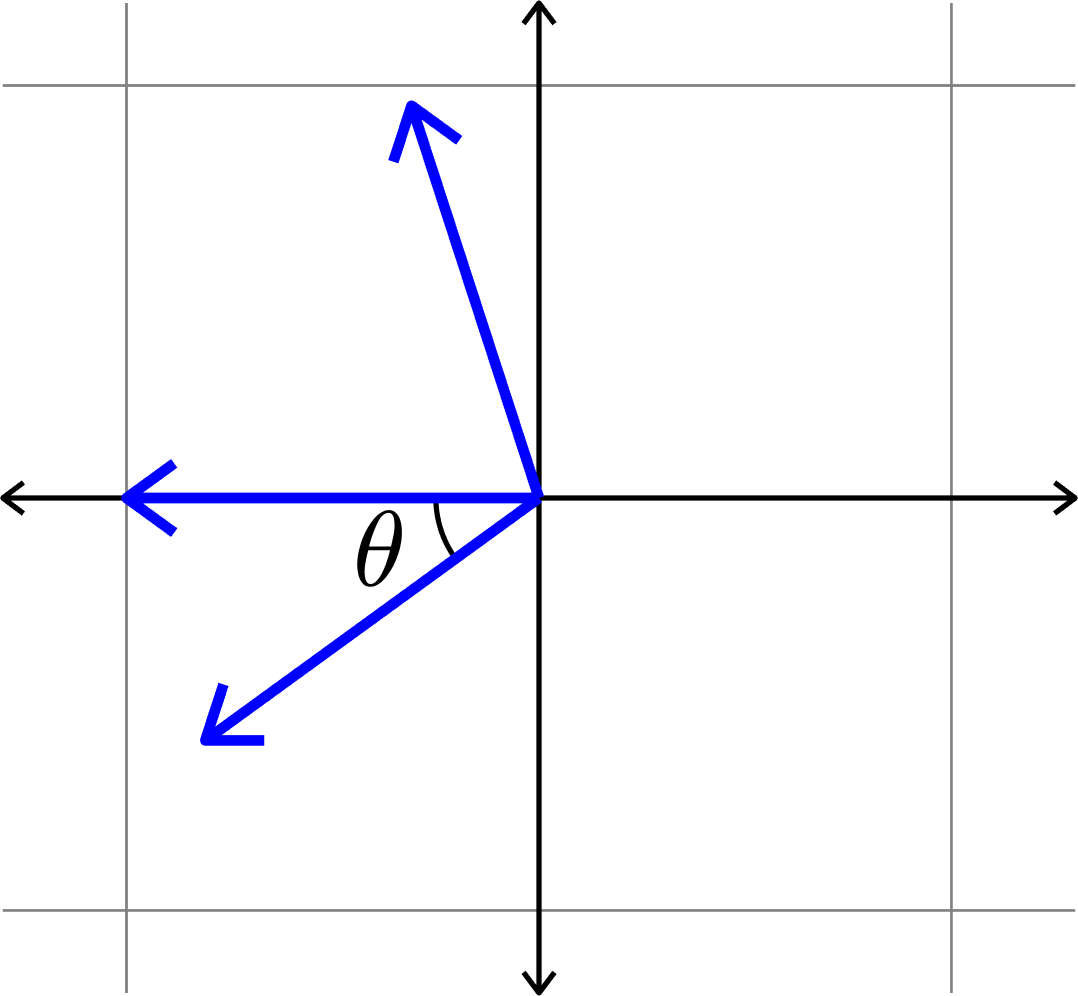
Vectors that are "Spread out"

Equiangular tight frames

ETFs from groups

\(\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

The design theory underneath

Real Flat ETFs

Some binary codes

Group divisible designs

ETFs and graphs

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

Measuring how "spread out" vectors are

\[\mu(\Phi) = \cos(\theta)\]

\(\mu(\Phi) = \cos(\theta)\)??

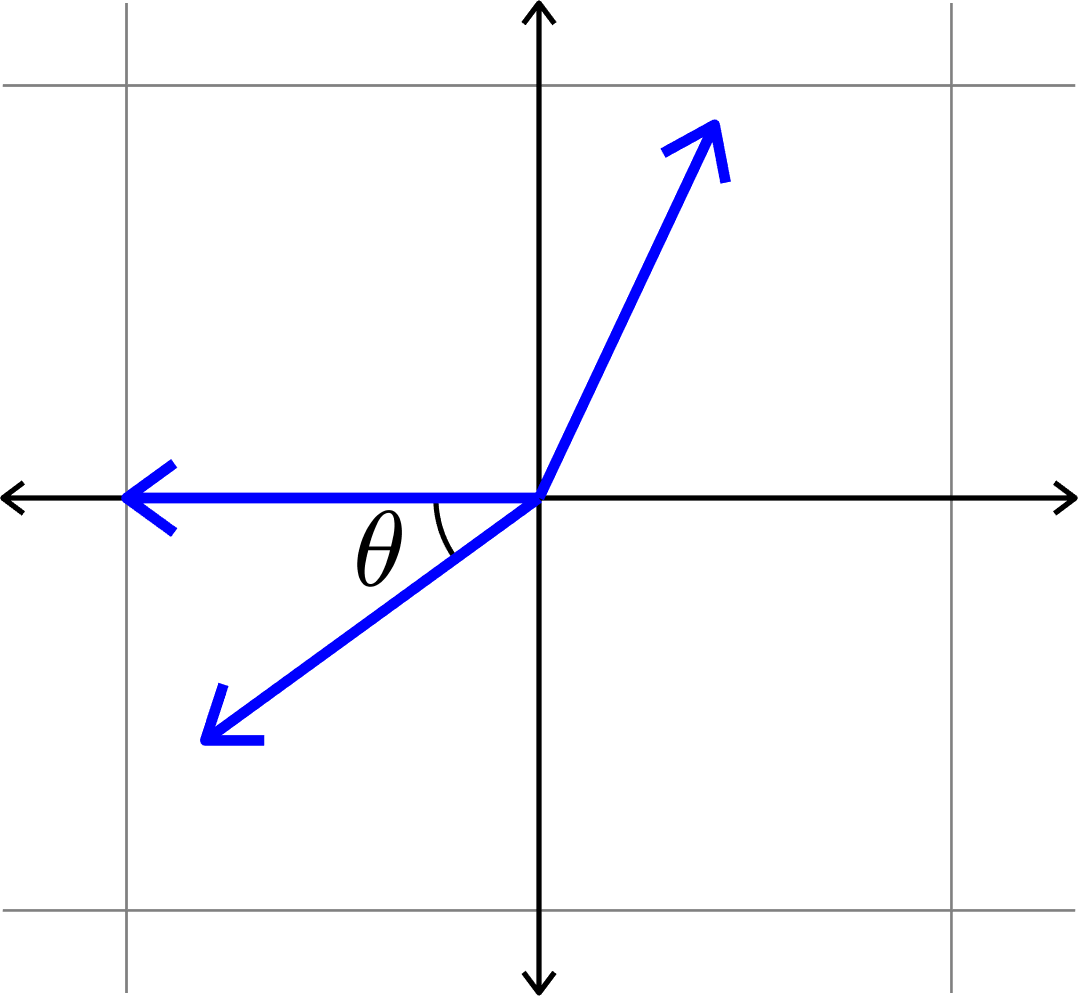
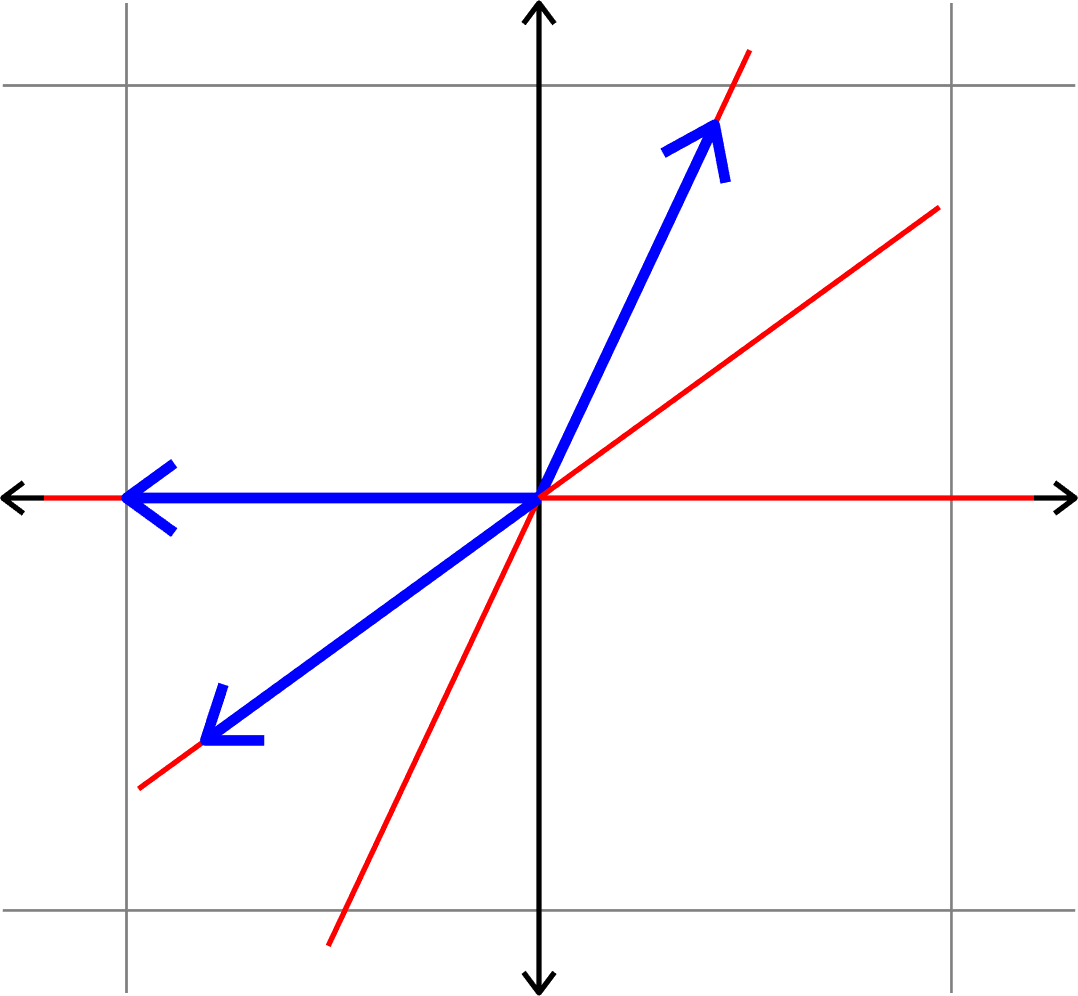
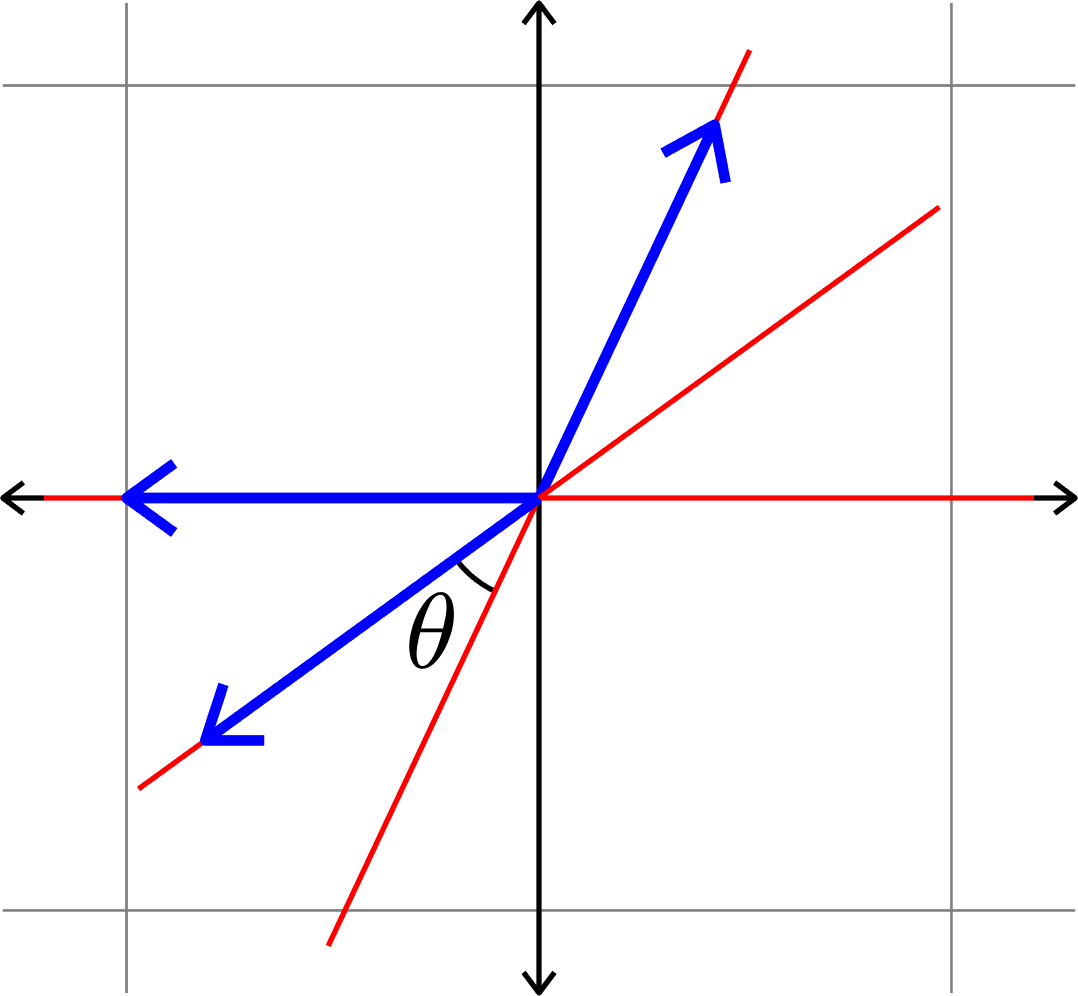
\(\mu(\Phi) = \cos(\theta)\)

Measuring how "spread out" vectors are

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

Example.

Measuring how "spread out" vectors are

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

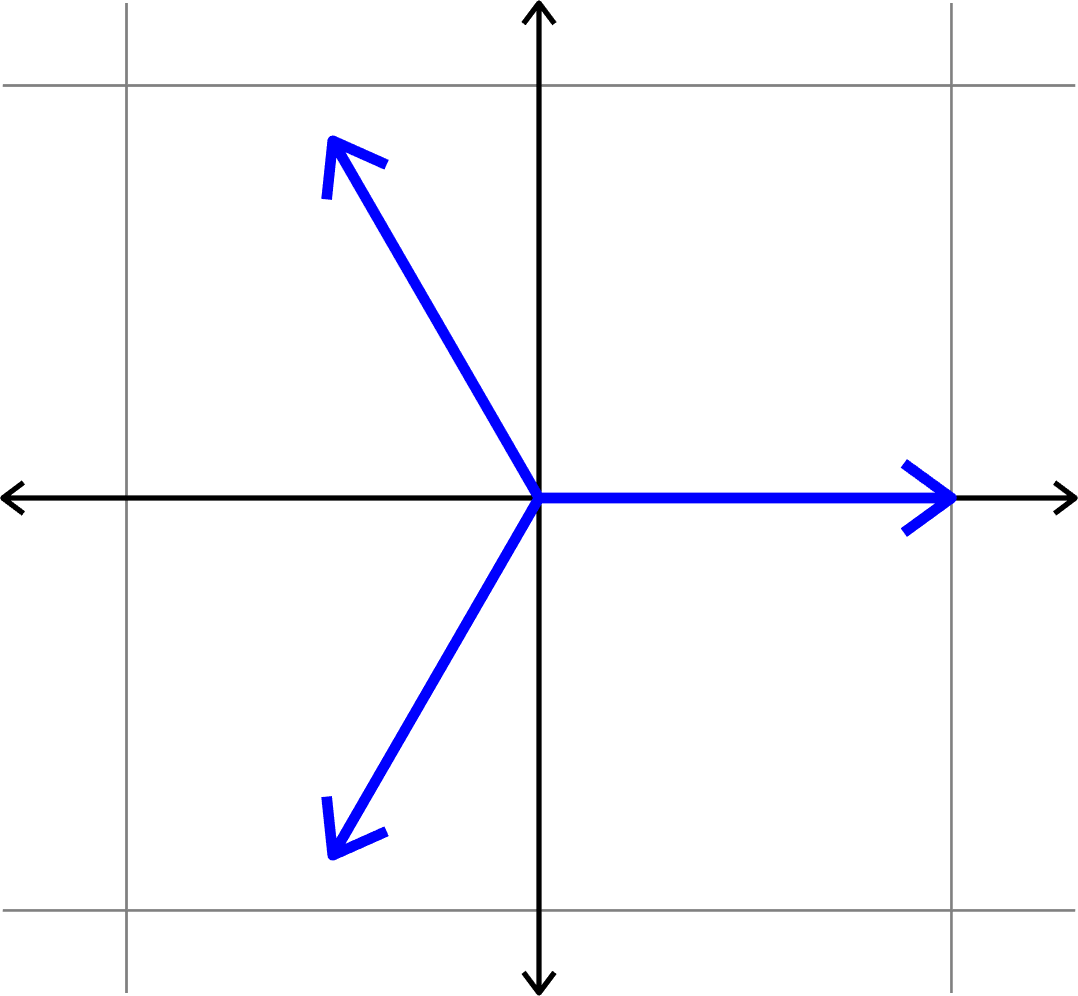
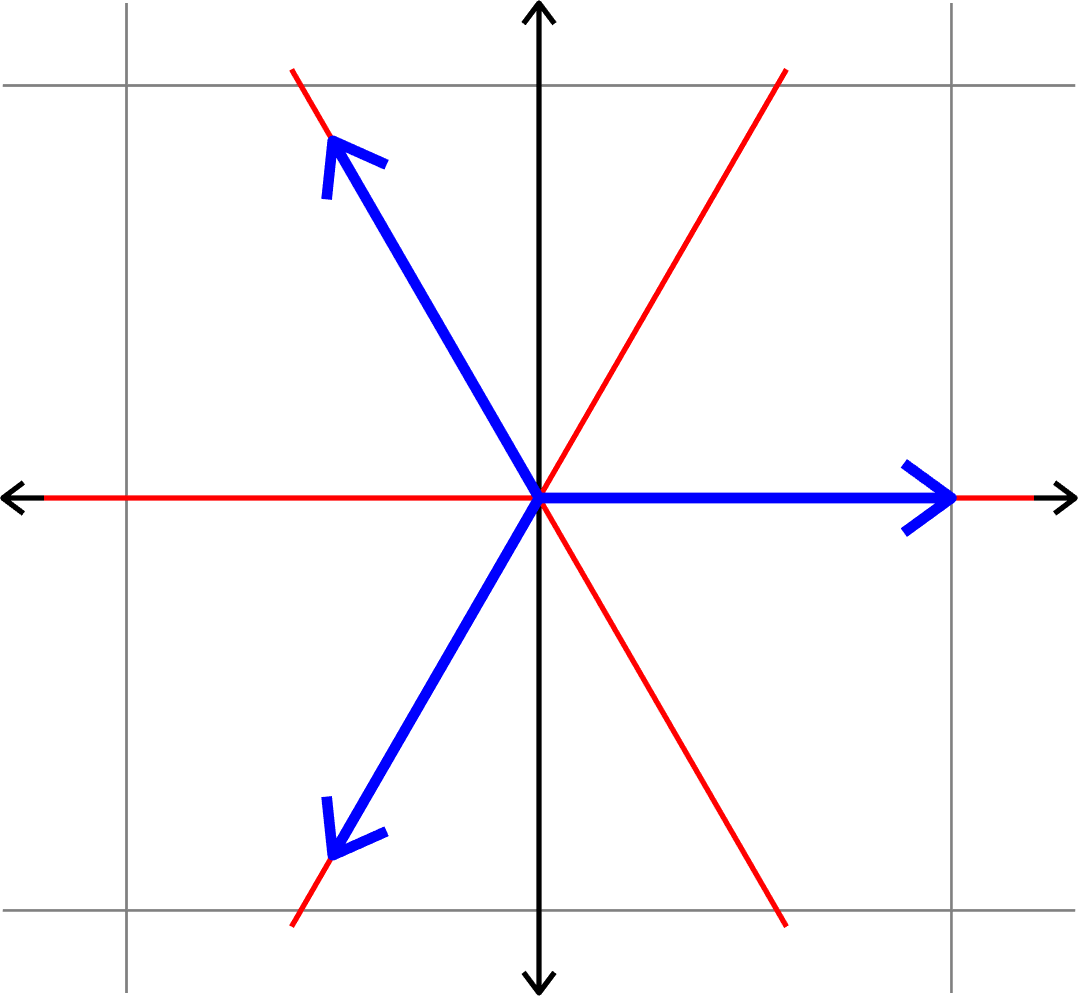
Vectors that are as spread out as possible

Theorem (the Welch bound). Given a collection of unit vectors

\(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{C}^d\), the coherence satisfies

\[\mu(\Phi)\geq \sqrt{\frac{N-d}{d(N-1)}}.\]

Equality holds if and only if the following two conditions hold:

Tight: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]
Equiangular: There is a constant \(\alpha\) such that \[|\langle\varphi_{i},\varphi_{j}\rangle| = \alpha\quad\text{for all }i\neq j.\]

Welch bound equality \(\Longleftrightarrow\) equiangular tight frame (ETF)

Tightness and short, fat matrices

Useful matrix representation: \(\quad\Phi = \begin{bmatrix} | & | & & |\\ \varphi_{1} & \varphi_{2} & \cdots & \varphi_{N}\\ | & | & & |\end{bmatrix}\)

Tightness: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]

( )

\(\Leftrightarrow\quad\Phi\Phi^{\ast} = AI\)

\(\Leftrightarrow\quad\) the rows of \(\Phi\) are orthogonal and equal norm

\(\langle v,\Phi\Phi^{\ast}v\rangle = \)

Examples of equiangular tight frames

Example 2. Consider the (multiple of a) unitary matrix

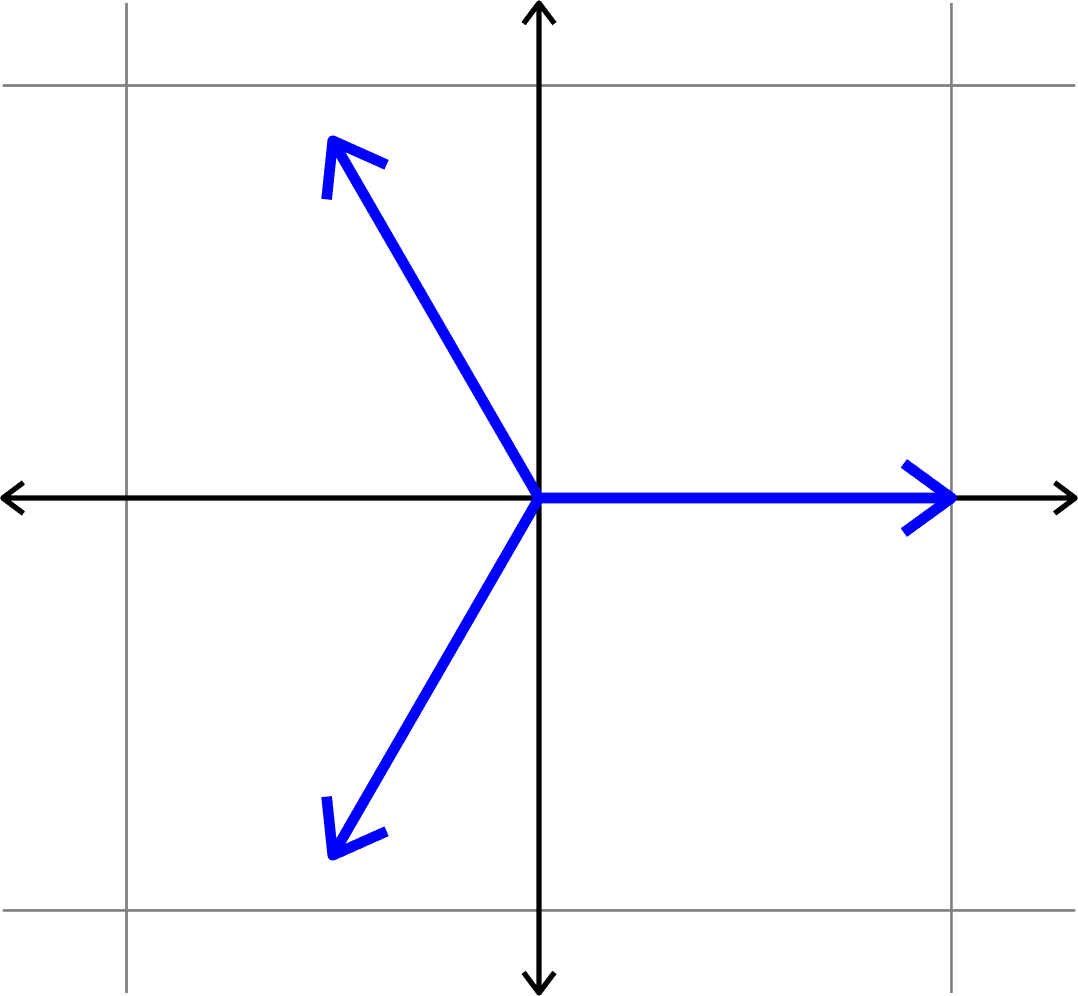
Example 1. Consider the (multiple of a) unitary matrix

\[\left[\begin{array}{rrrr}1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]

\[\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]

\[\left[\begin{array}{rrrr} 1 & 1 & 1\\ \sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]

\[\left[\begin{array}{rrrr}\sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]

Examples of equiangular tight frames

Example 3.

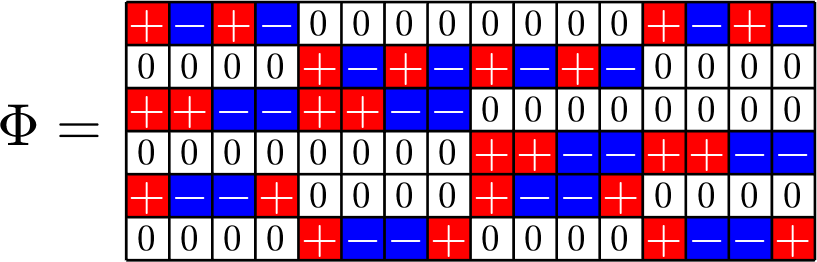
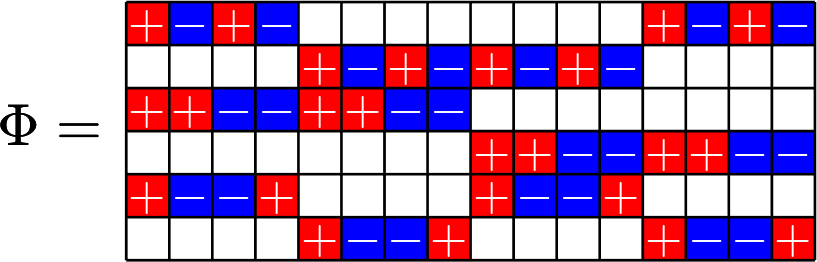
Theme of the talk:

\(\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\)

Some ETFs

arise from

groups...

a lot more ETFs

arise from

combinatorial designs!

M

Roadmap for this talk

Compressed Sensing

Vectors that are "Spread out"

Equiangular tight frames

ETFs from groups

\(\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

The design theory underneath

Real Flat ETFs

Some binary codes

Group divisible designs

ETFs and graphs

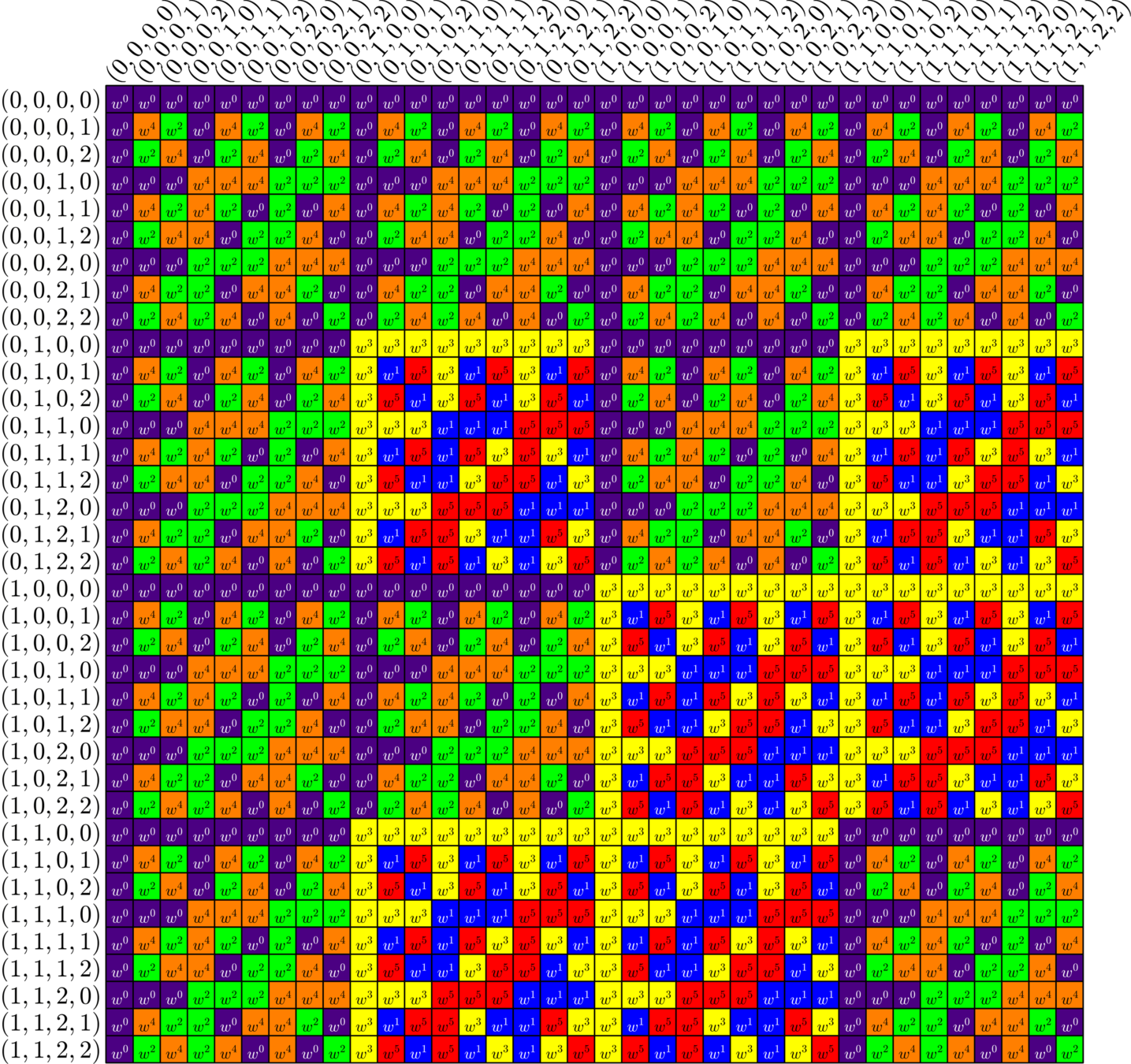
\[\Z_{7}\left\{\begin{array}{c} 0\\ 1\\ 2\\ 3\\ 4\\ 5\\ 6 \end{array}\right. \left[\begin{array}{ccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^3 & \omega^6 & \omega^2 & \omega^5 & \omega & \omega^4\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3\\ 1 & \omega^5 & \omega^3 & \omega & \omega^6 & \omega^4 & \omega^2\\ 1 & \omega^6 & \omega^5 & \omega^4 & \omega^3 & \omega^2 & \omega \end{array}\right]\]

\[\begin{array}{c} 1\\ 2\\ 4 \end{array}\left[\begin{array}{ccccccc} 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3 \end{array}\right]\]

Rows from a DFT

(\(\omega = e^{2\pi i/7}\))

\[\Phi = \left[\begin{array}{ccccccc} 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3 \end{array}\right]\]

Rows from a DFT

\(\Phi\) is tight, since it is rows out of a unitary.

\(\Phi\) is equiangular, since \(D=\{1,2,4\}\subset\Z_{7}\) is a difference set.

That is, if we look at the difference table

\[\begin{array}{r|rrr} - & 1 & 2 & 4\\ \hline 1 & 0 & 6 & 4\\ 2 & 1 & 0 & 5\\ 4 & 3 & 2 & 0 \end{array}\]

every nonidentity group element shows up the same number of times

Difference sets \(\Rightarrow\) equiangular?

\(\Phi^{\ast}\Phi = \operatorname{circ}(\hat{\mathbf{1}}_{D})\)

\(|\Phi^{\ast}\Phi|^{2} = \operatorname{circ}\big(|\hat{\mathbf{1}}_{D}|^{2}\big)\)

\(|\hat{\mathbf{1}}_{D}|^{2} = \hat{\mathbf{1}}_{D}\odot\overline{\hat{\mathbf{1}}_{D}} = \mathcal{F}\big(\mathbf{1}_{D}\ast \mathbf{1}_{-D}\big) \)

Want \(\Phi=\) ETF, i.e., \(|\hat{\mathbf{1}}_{D}|^{2} = a\delta_{0}+b\mathbf{1}_{G} = \textit{spike + flat}\)

\(\mathcal{F}(\textit{spike + flat}) = \textit{spike + flat}\)

\(\mathbf{1}_{D}\ast \mathbf{1}_{-D}=\textit{spike + flat}\quad\Longleftrightarrow\quad D\) is a difference set

Suppose: \(\Phi=(\text{rows of DFT indexed by }D)\)

Meme of the talk:

\(\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\)

Some ETFs

arise from

McFarland Difference Sets...

a lot more ETFs

arise from

Steiner systems!

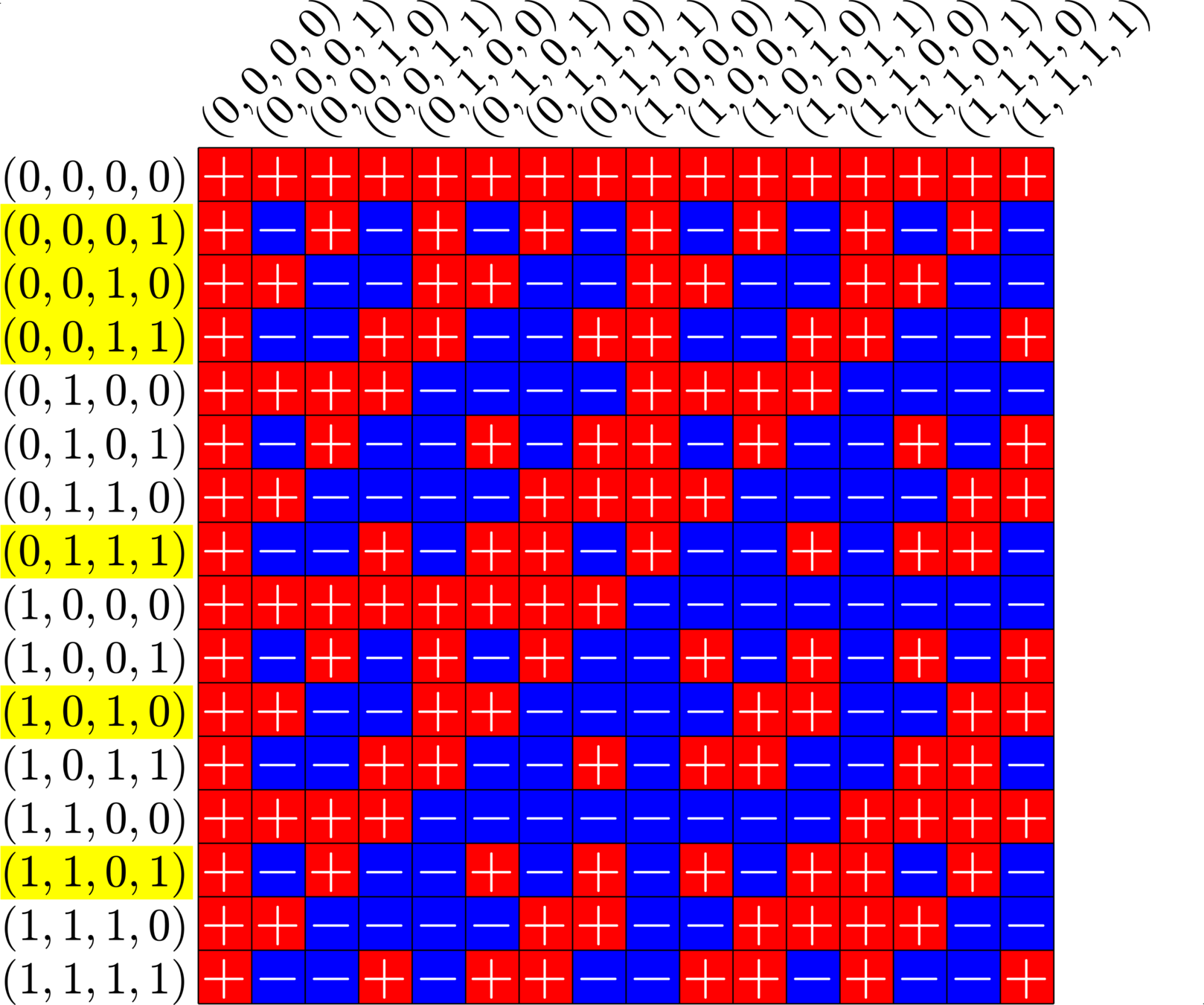
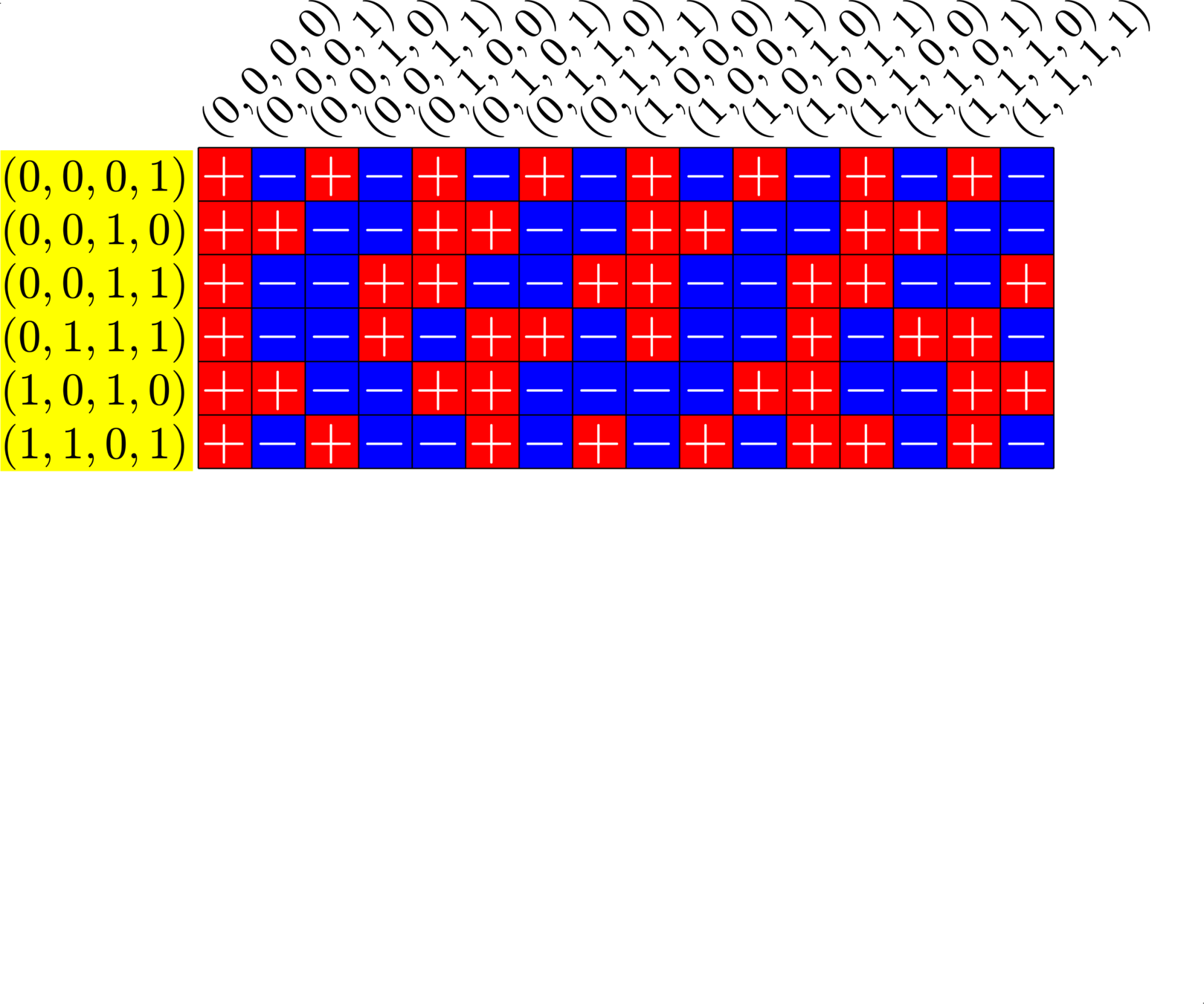
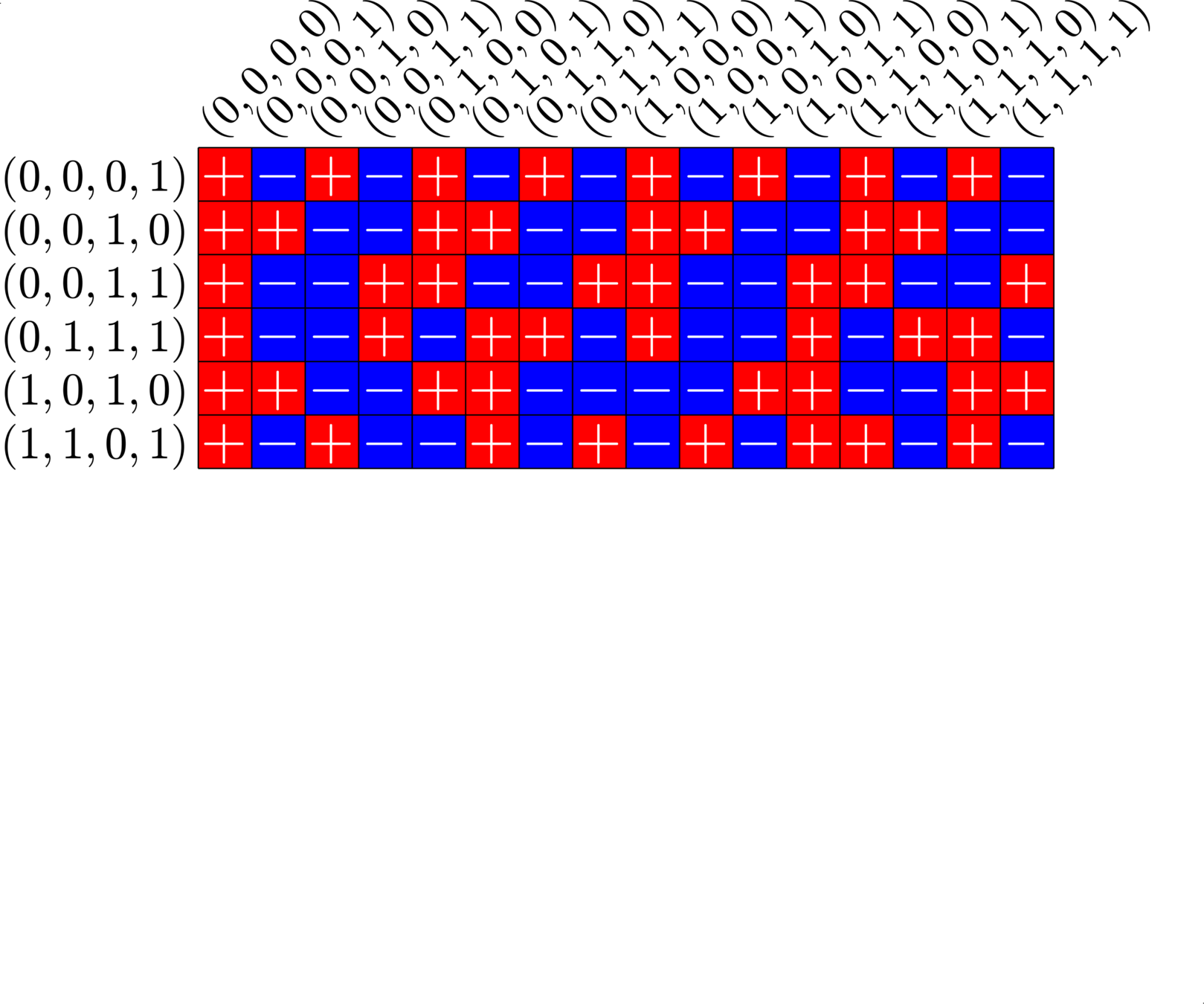
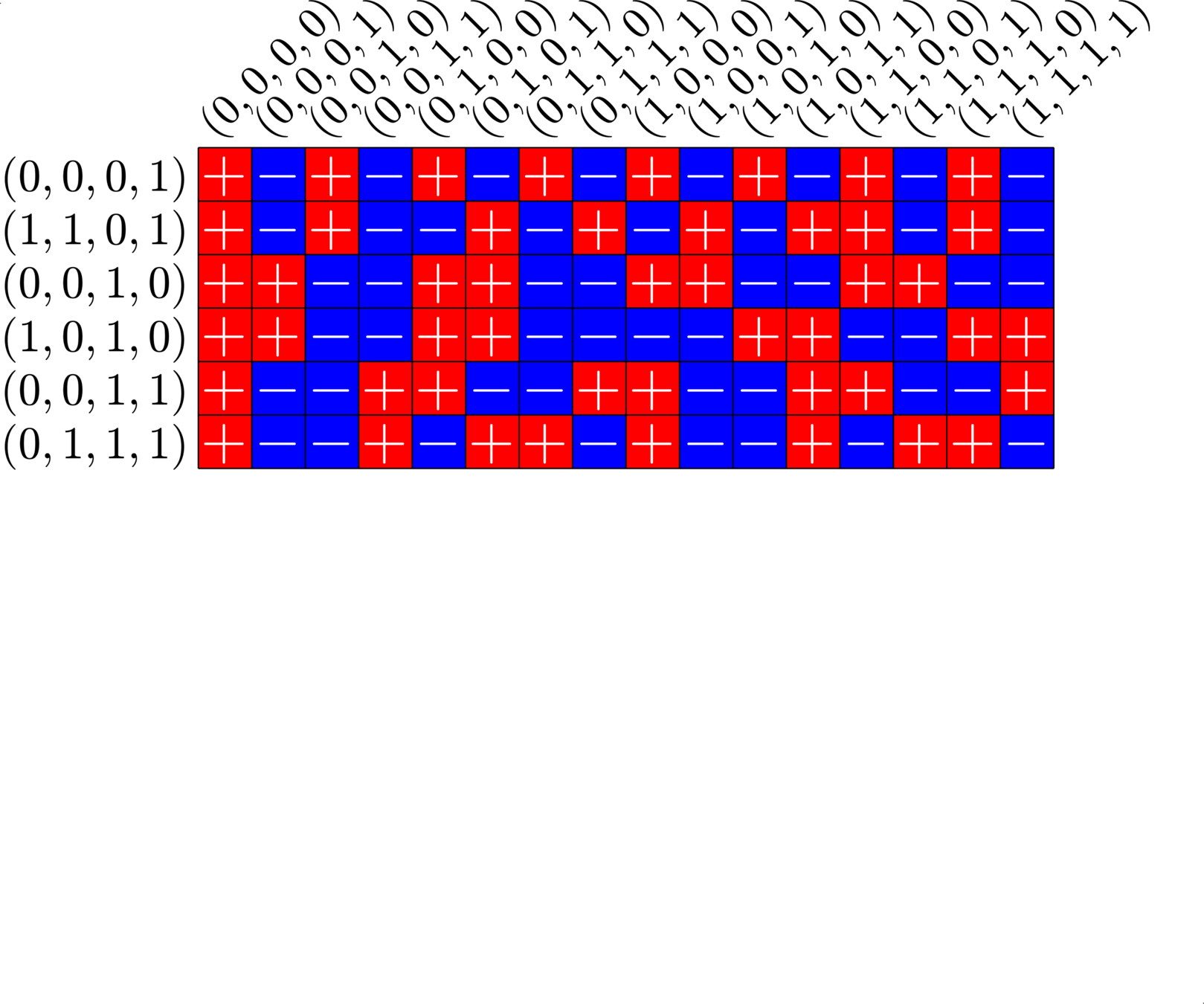
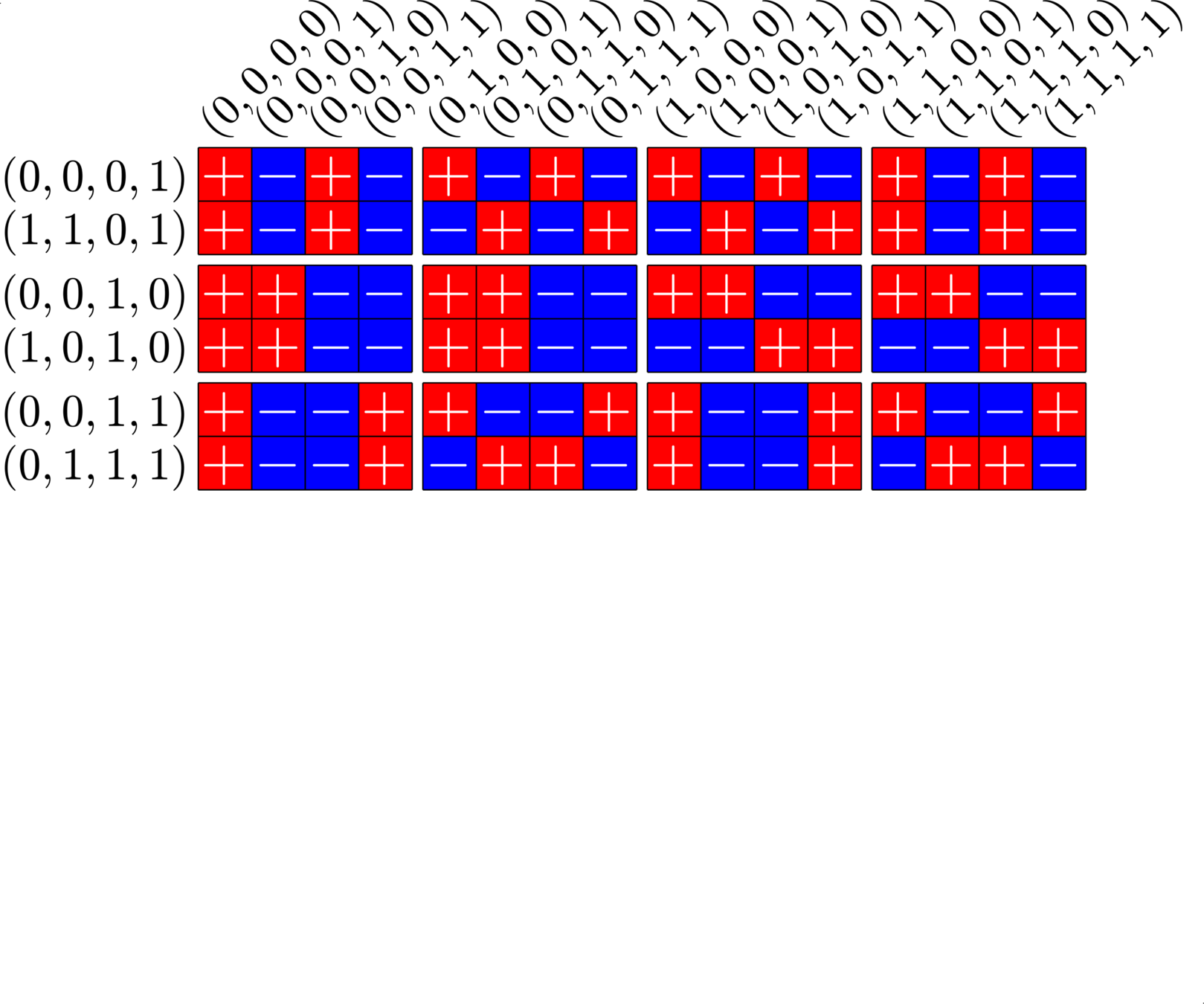
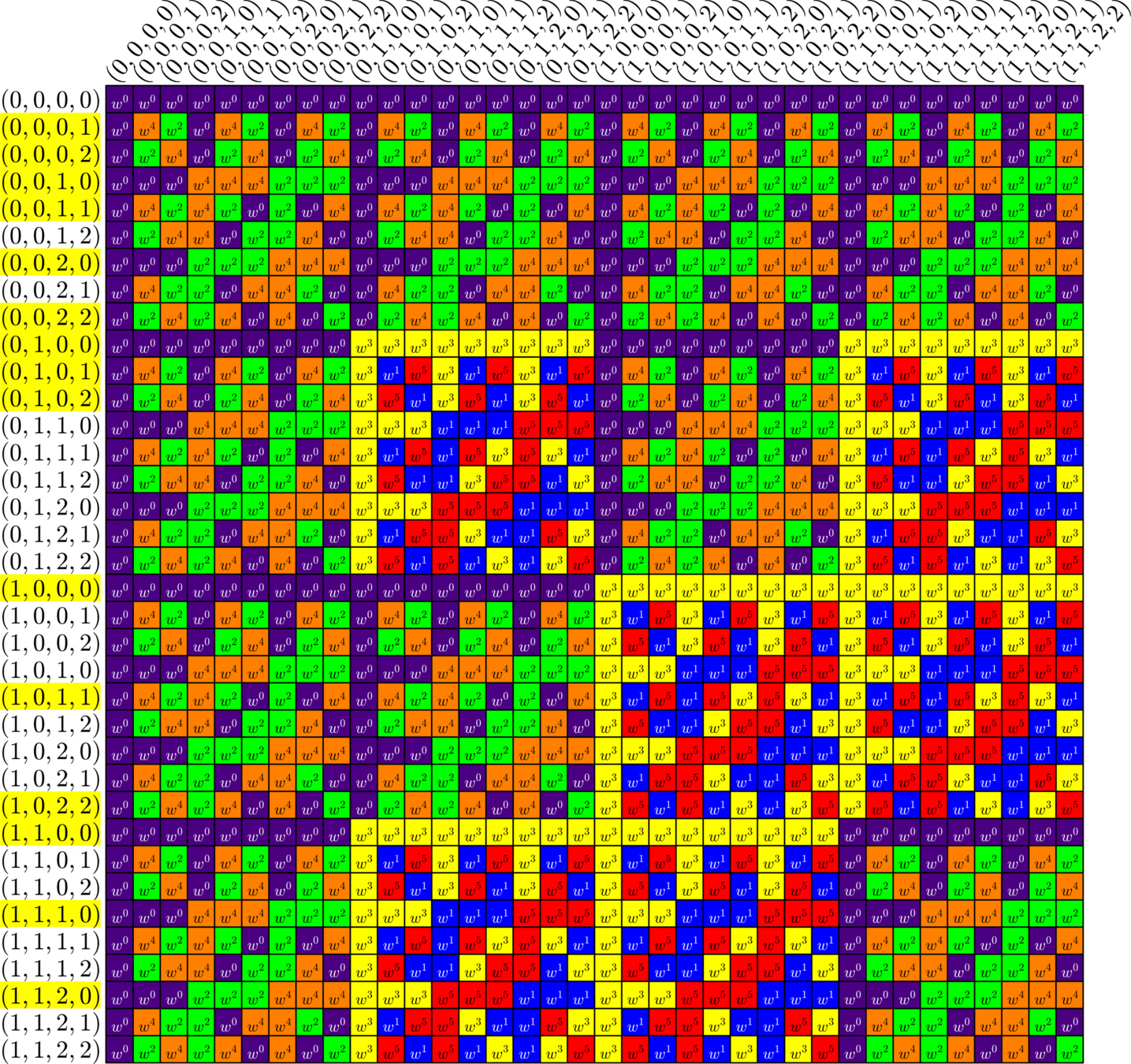
\[\begin{array}{c|cccccc} & (0,0,0,1) & (1,1,0,1) & (0,0,1,0) & (1,0,1,0) & (0,0,1,1) & (0,1,1,1)\\ \hline (0,0,0,1) & (0,0,0,0) & (1,1,0,0) & (0,0,1,1) & (1,0,1,1) & (0,0,1,0) & (0,1,1,0)\\ (1,1,0,1) & (1,1,0,0) & (0,0,0,0) & (1,1,1,1) & (0,1,1,1) & (1,1,1,0) & (1,0,1,0)\\ (0,0,1,0) & (0,0,1,1) & (1,1,1,1) & (0,0,0,0) & (1,0,0,0) & (0,0,0,1) & (0,1,0,1)\\ (1,0,1,0) & (1,0,1,1) & (0,1,1,1) & (1,0,0,0) & (0,0,0,0) & (1,0,0,1) &(1,1,0,1)\\ (0,0,1,1) & (0,0,1,0) & (1,1,1,0) & (0,0,0,1) & (1,0,0,1) & (0,0,0,0) & (0,1,0,0)\\ (0,1,1,1,) & (0,1,1,0) & (1,0,1,0) & (0,1,0,1) & (1,1,0,1) & (0,1,0,0) & (0,0,0,0) \end{array}\]

\[D=\{(0,0,0,1),(0,0,1,0),(0,0,1,1),(0,1,1,1),(1,0,1,0),(1,1,0,1)\}\]

is a (McFarland) difference set in \(G=\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

A McFarland difference set

The subgroup \[H=\Z_{2}\times \Z_{2}\times 0\times 0\leqslant G\] is disjoint from \(D\).

A McFarland difference set

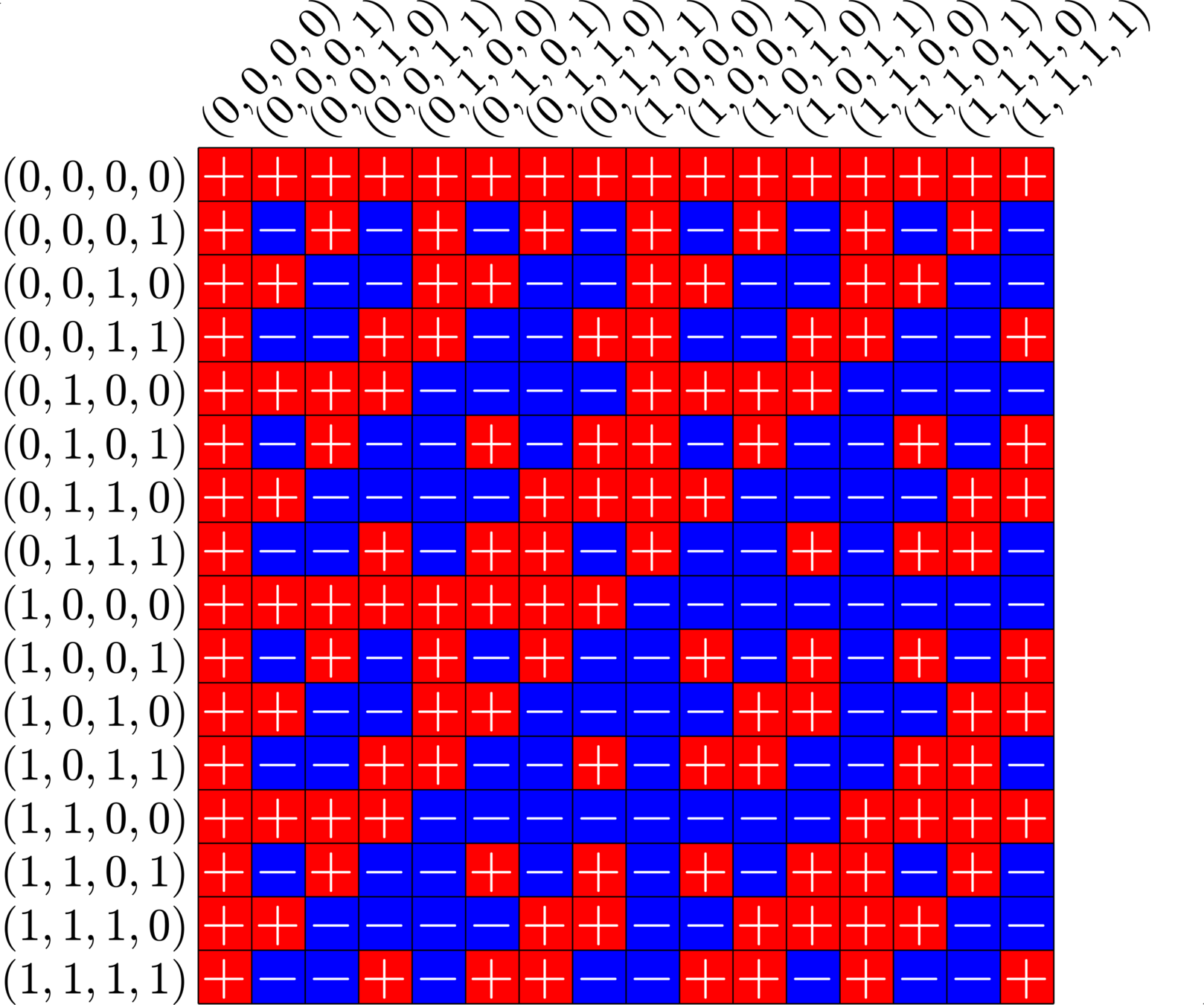
Steiner Systems

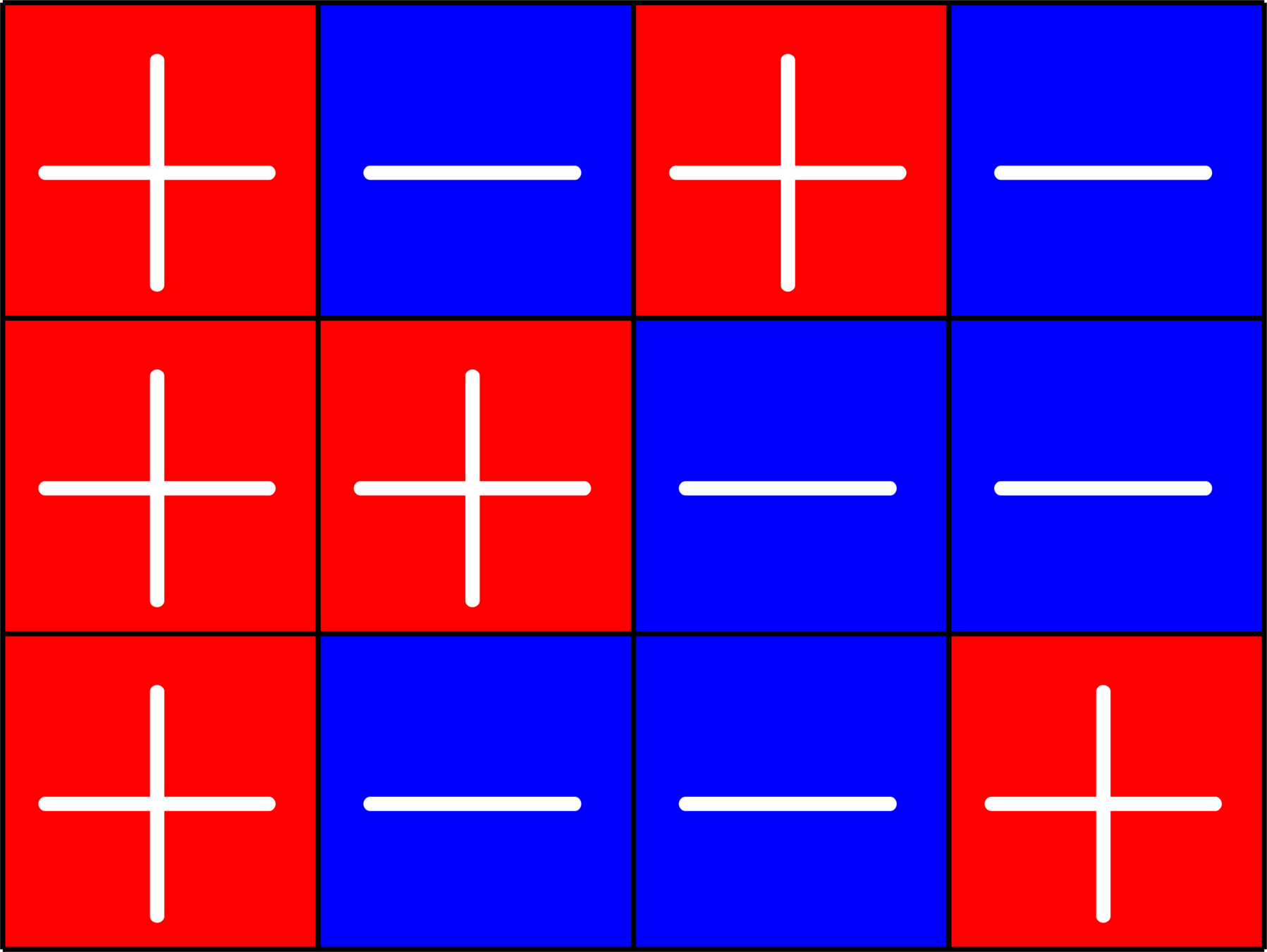
Definition. A \((2,k,v)\)-Steiner system is a \(\{0,1\}\)-matrix \(X\) such that:

Each row of \(X\) has exactly \(k\) ones.
Each column of \(X\) has exactly \(r=\frac{v-1}{k-1}\) ones.
The dot product of any pair of distinct columns is one.

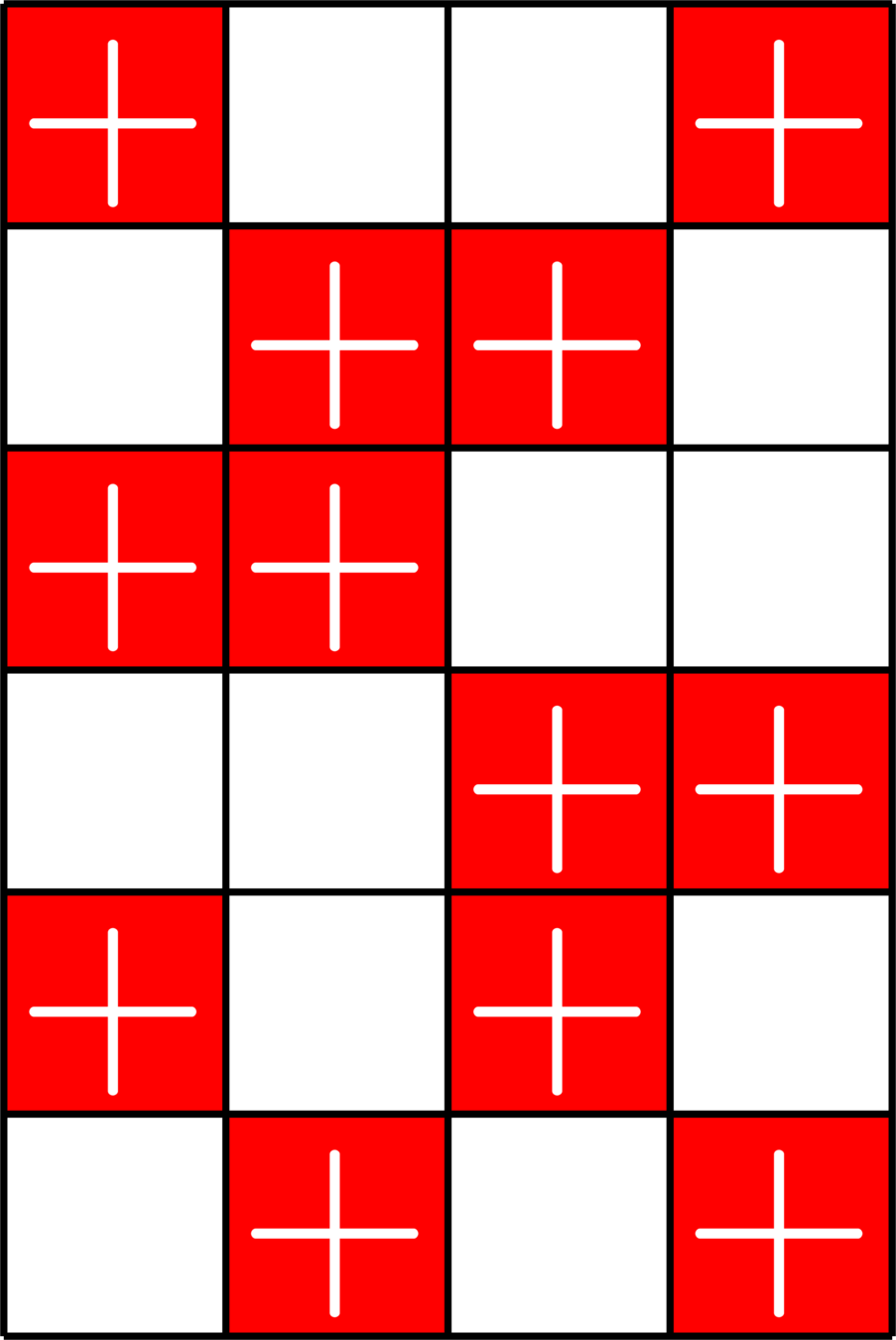
Example. The matrix

\(X = \)

is a \((2,2,4)\)-Steiner system.

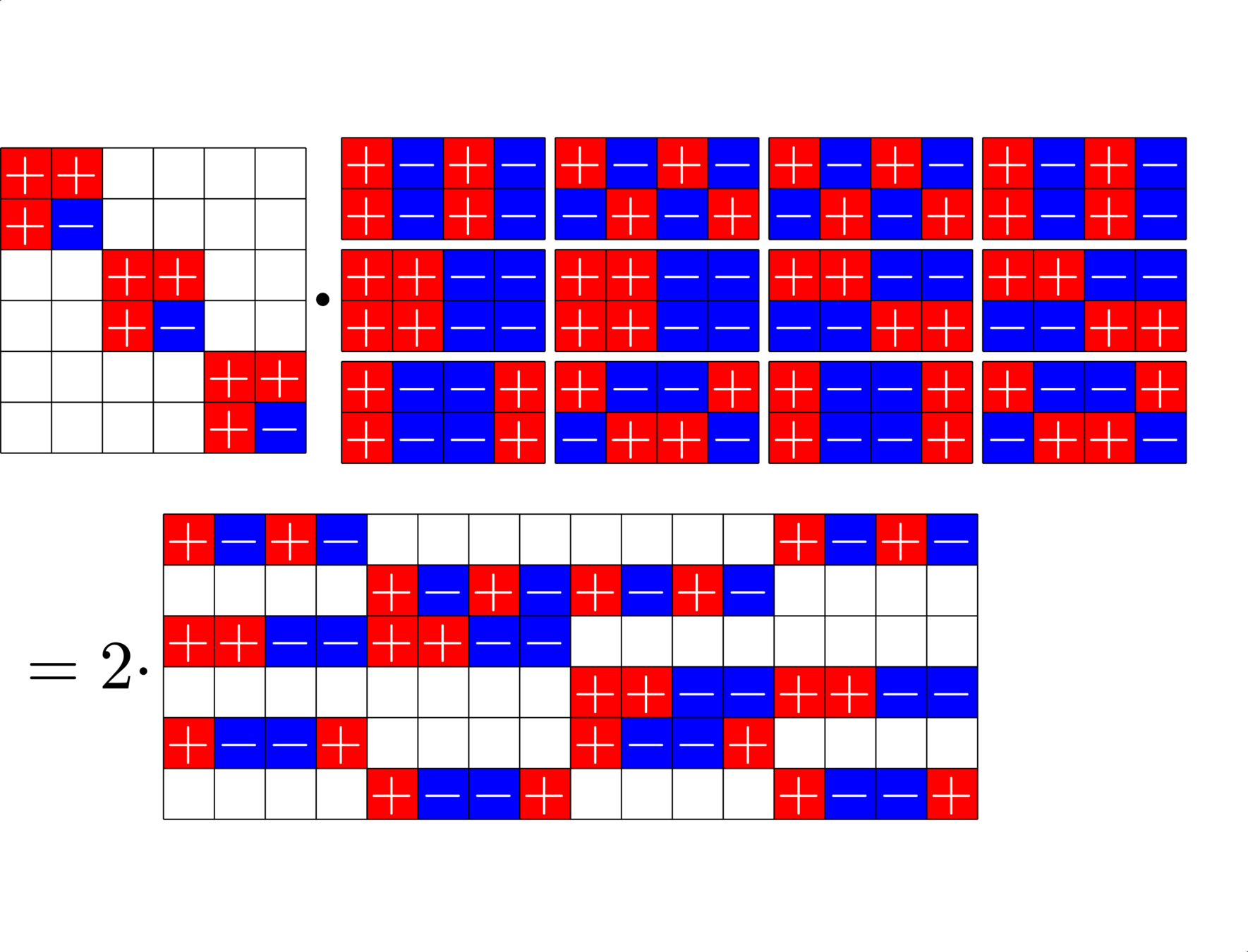
The Star Product

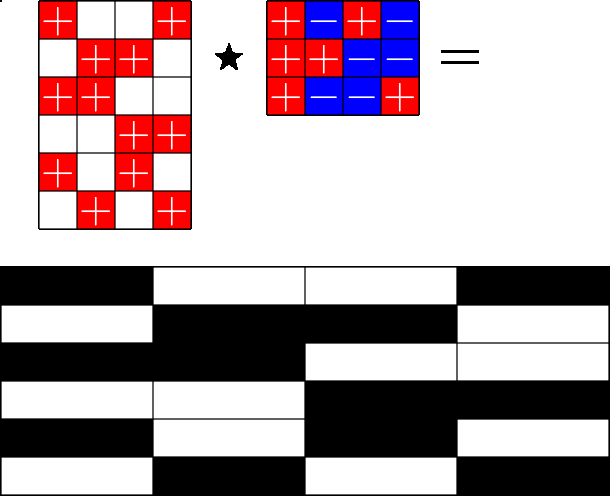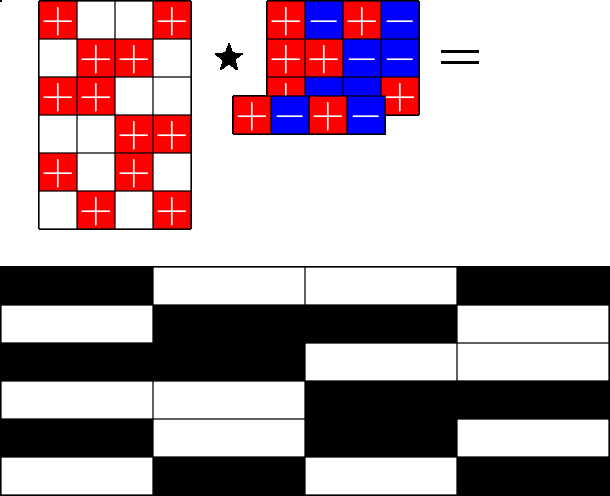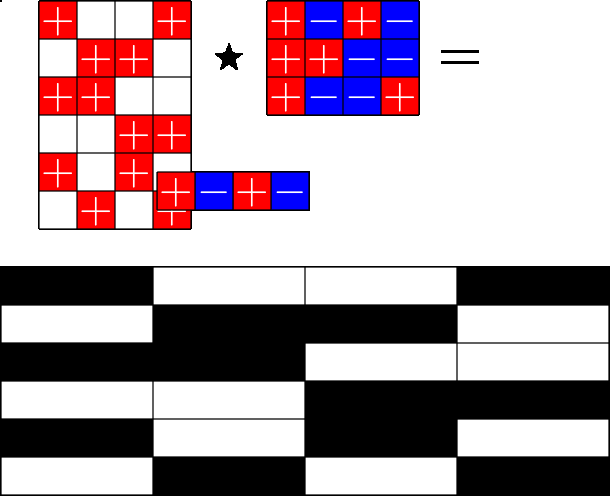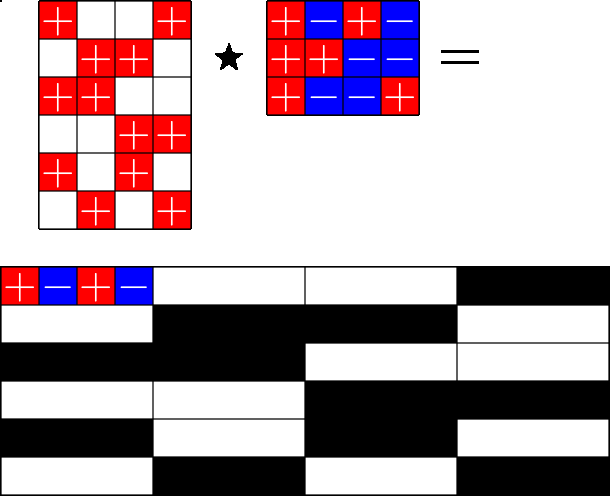
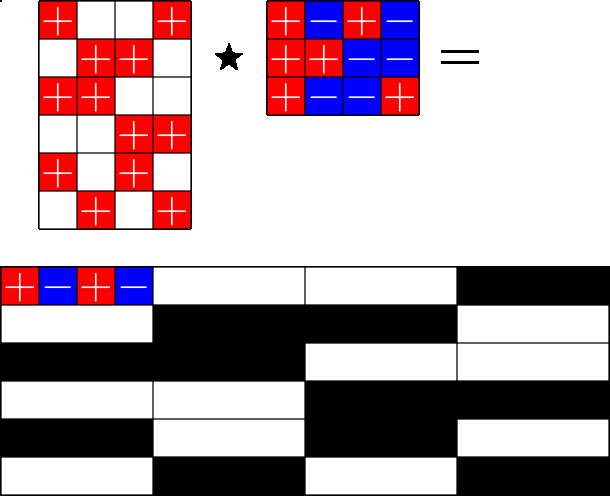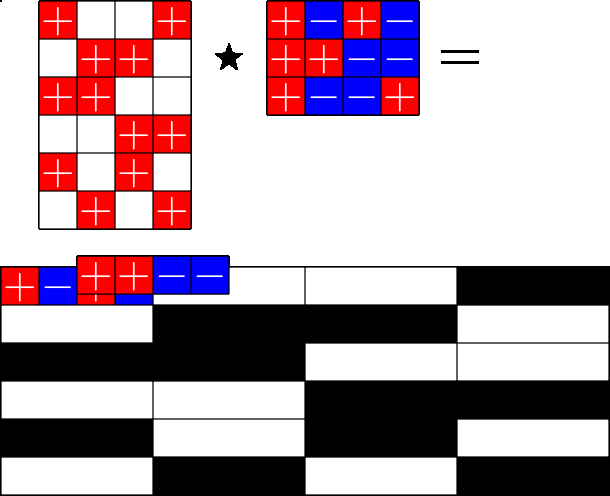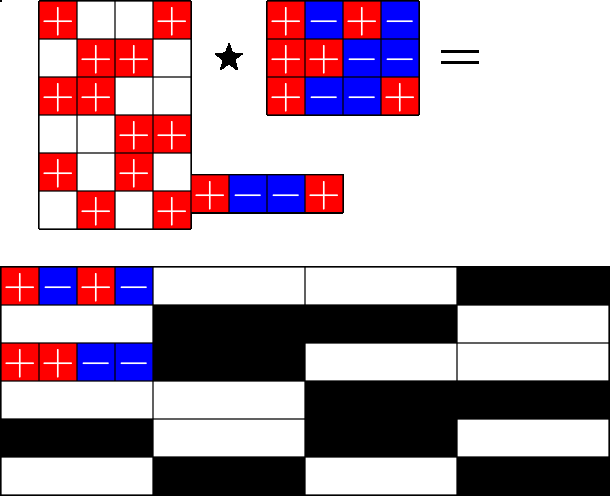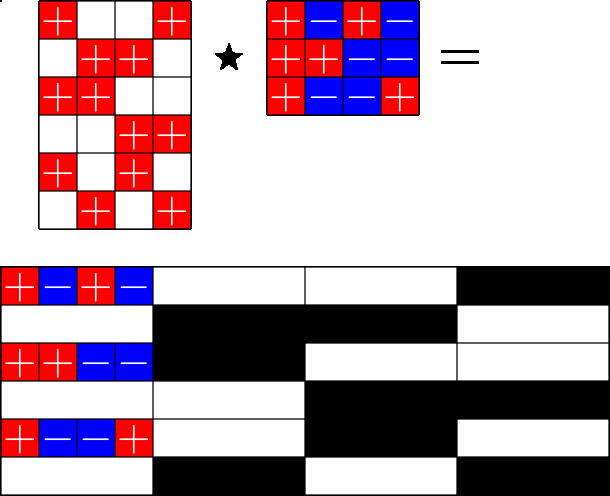
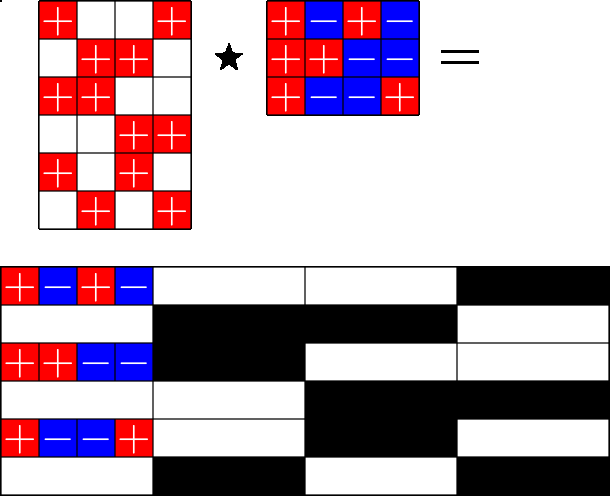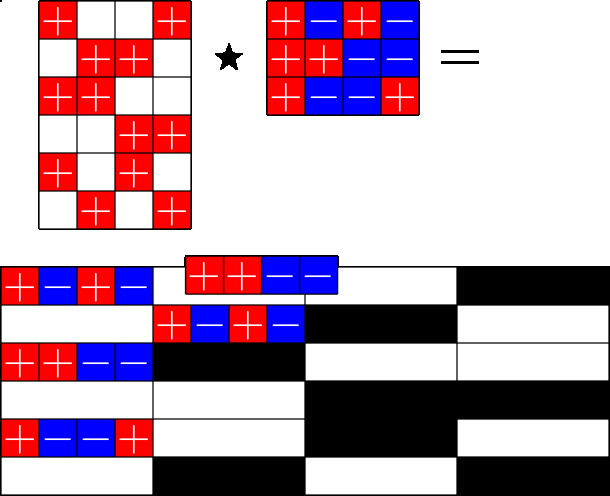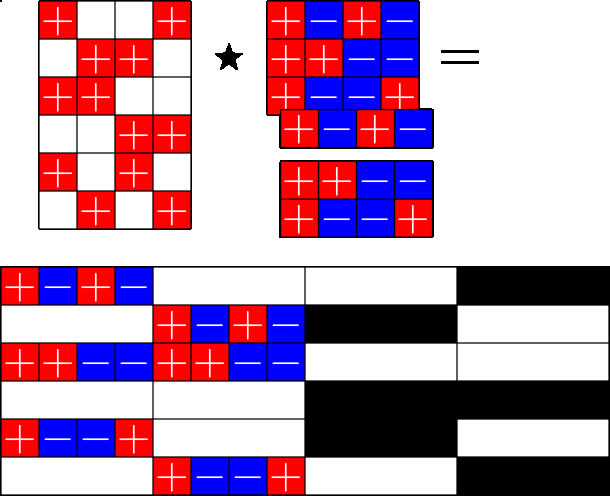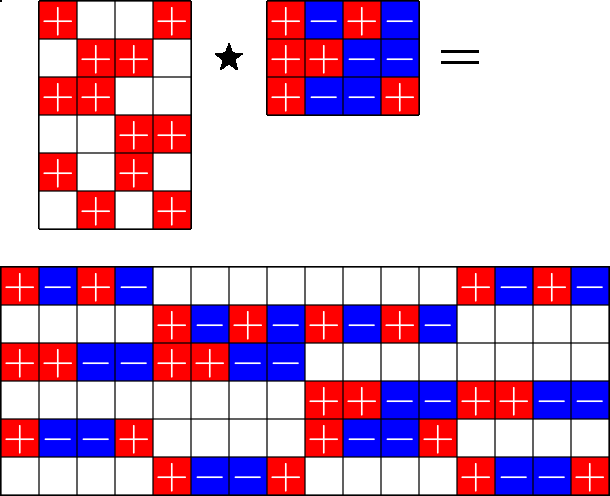
A way to construct lots of ETFs

\(=\)

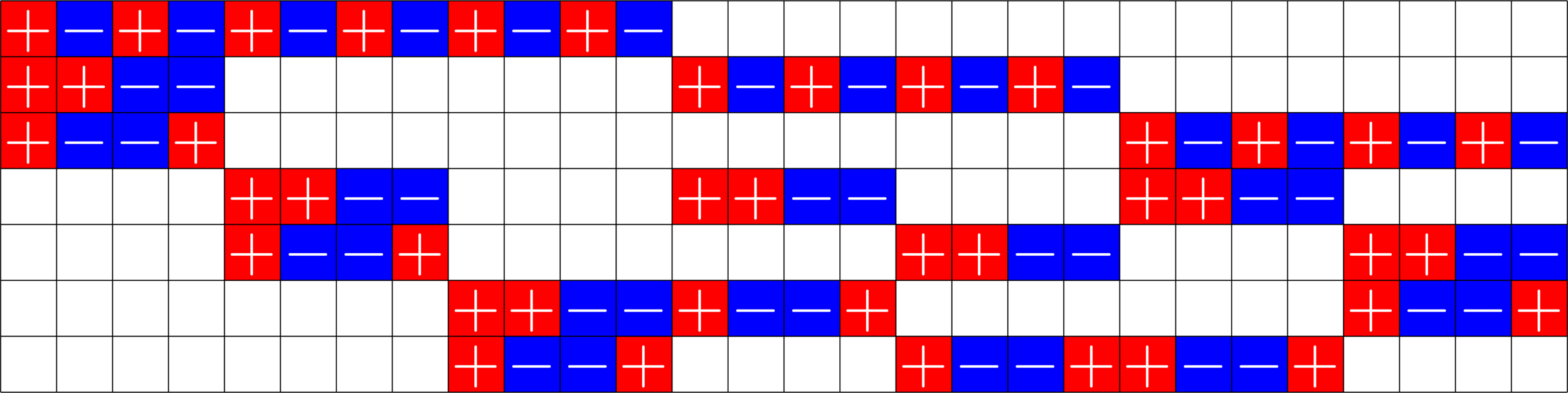
Take a Steiner system with \(r\) ones per column

and an \(r\times (r+1)\) ETF with unimodular entries

The Star product is a "Steiner" ETF

Roadmap for this talk

Compressed Sensing

Vectors that are "Spread out"

Equiangular tight frames

ETFs from groups

\(\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

The design theory underneath

Real Flat ETFs

Some binary codes

Group divisible designs

ETFs and graphs

Real Flat ETFs

ETFs with all \(\pm 1\) entries: Real Flat ETFs

Why real flat ETFs?

Waveform design: maximize \(\|x\|_{2}\) subject to \(\|x\|_{\infty}\leq B\) (minimal peak-to-average power ratio)
Quasi-symmetric designs
Grey-Rankin equality binary codes

Real Flat ETFs

\(=\)

Real Flat ETFs

Example. A \(276\times 576\) real ETF

Real Flat ETFs

Theorem (J '13)

\(N\times N\) Hadamard matrix \(\Longrightarrow\) \(N(2N-1)\times 4N^2\) real flat ETF

Previously known real flat ETFs:

\(N = 2^k\) harmonic ETFs on \(\mathbb{Z}_{2}^{2k+2}\)
\(N = 6\) [Bracken, McGuire, & Ward, 2006]

Theorem (Mixon, J, Fickus '13)

Real Flat

ETFs

Grey-Rankin

equality

binary codes

1-1 correspondence

We can also construct a real flat \(317886556\times 1907416992\) ETF.

Roadmap for this talk

Compressed Sensing

Vectors that are "Spread out"

Equiangular tight frames

ETFs from groups

\(\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

The design theory underneath

Real Flat ETFs

Some binary codes

Group divisible designs

ETFs and graphs

Meme of the talk:

\(\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{3}\times\mathbb{Z}_{3}\)

Some ETFs

arise from

Spence Difference Sets...

a lot more ETFs

arise from

Group Divisible

Designs!

Ex:

\(G\)

\( \mathbb{Z}_{2}\)

\(\times\)

\(\mathbb{Z}_{2}\)

\(\times\)

\(\mathbb{Z}_{3}\)

\(\times\)

\(\mathbb{Z}_{3}\)

\(=\)

\(\bigotimes\)

\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]

\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\[\cong\]

Unitary transformation

\(I_{3}\otimes\)(\(2\times 3\) ETF)

\(3\times 4\) ETF with unimodular entries

???

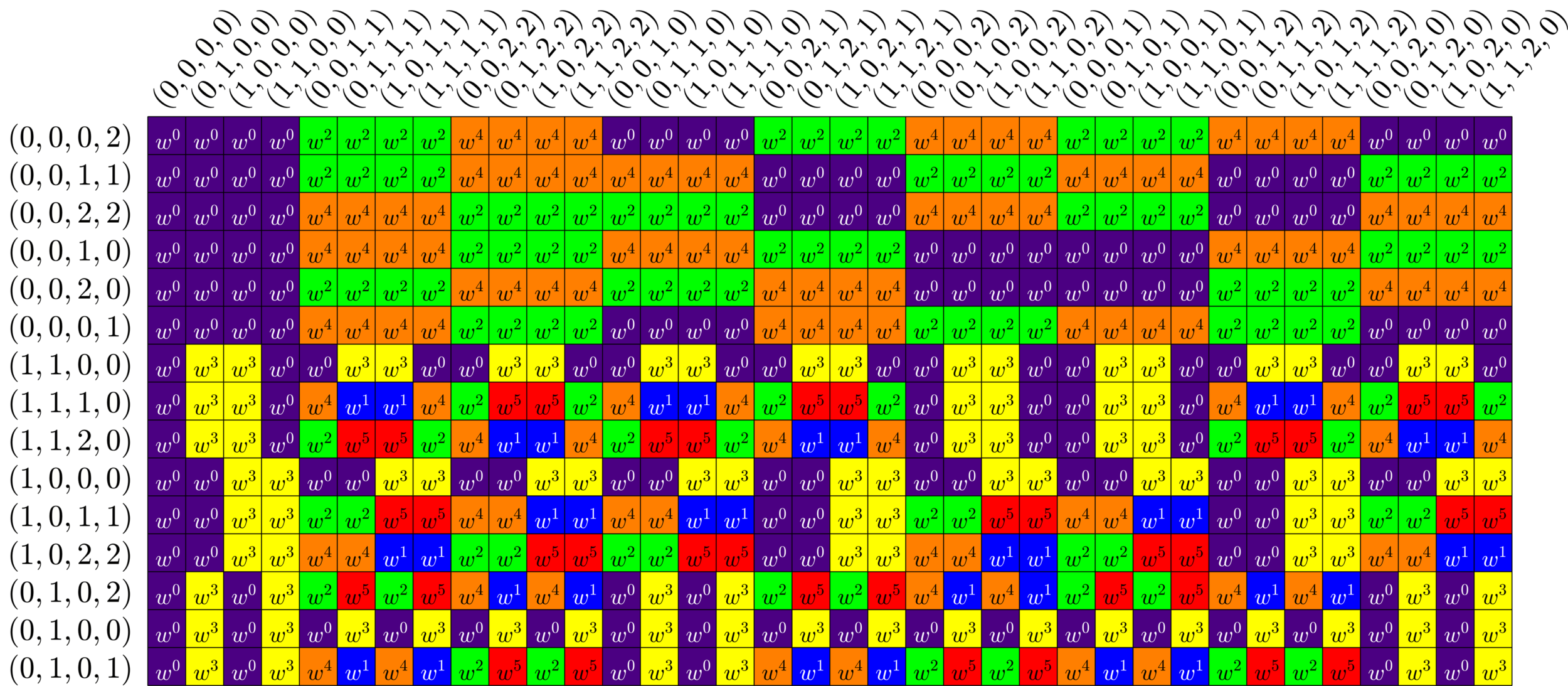
Group Divisible Designs

Definition. A \(K\)-GDD of type \(M^{U}\) is a \(\{0,1\}\)-matrix \(X\) such that:

\(X\) has \(UM\) columns.
Each row of \(X\) has \(K\) ones.
\(X^{\top}X = R\cdot I_{UM}+J_{UM}-(I_{U}\otimes J_{M})\) for some \(R\in\N\)

Example. The following is a \(3\)-GDD of type \(3^3\):

\(X = \)

\(X^{\top}X = \)

ETFs from GDDs

Theorem (Fickus, J '19). Given a

\(d\times n\) ETF

\(k\)-GDD of type \(M^{U}\)

and

provided certain integrality conditions hold, there exists a \(D\times N\) ETF with \(D>d\), \(N>n\) and \(\frac{D}{N}\approx \frac{d}{n}.\)

Real ETFs and Graphs

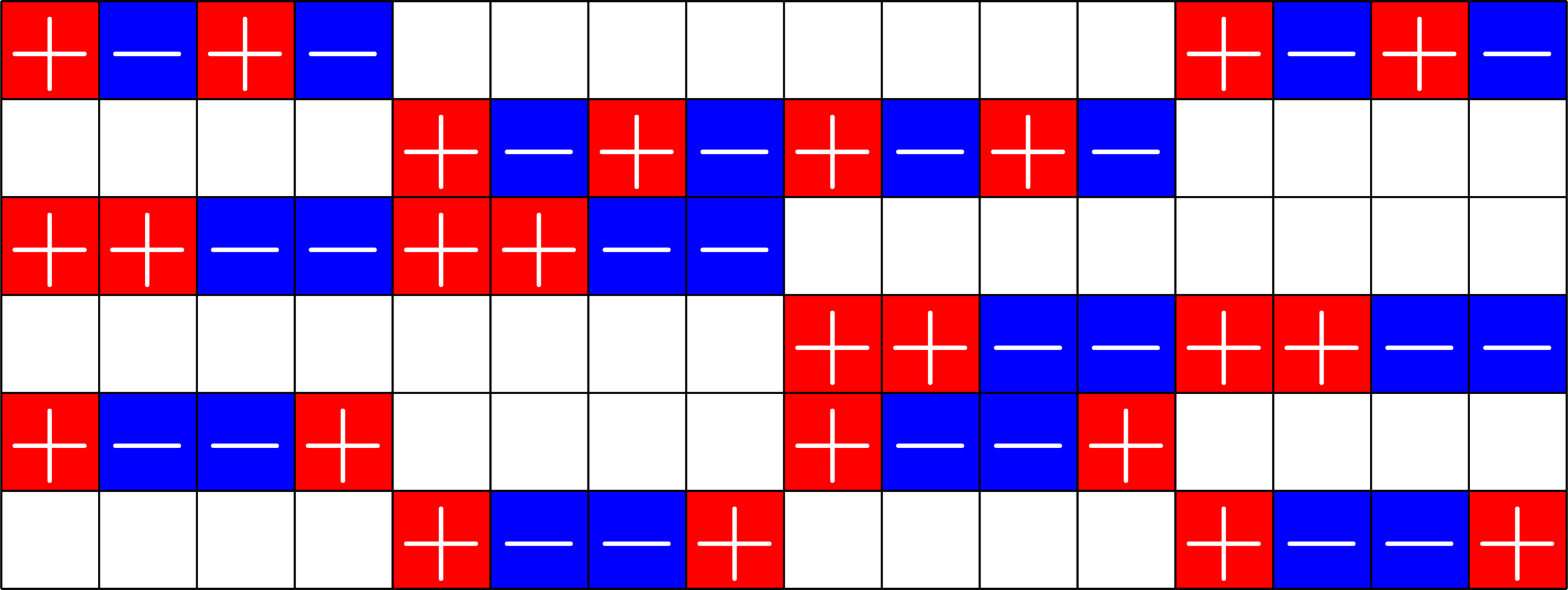
\(\Phi=\)

Given a real ETF \(\Phi\)
Normalize so that all dot products with the first vector are positive.

Real ETFs and Graphs

\(\Phi^{\top}\Phi=\)

Given a real ETF \(\Phi\)
Normalize so that all dot products with the first vector are positive.
Look at the gram matrix \(\Phi^{\top}\Phi\)

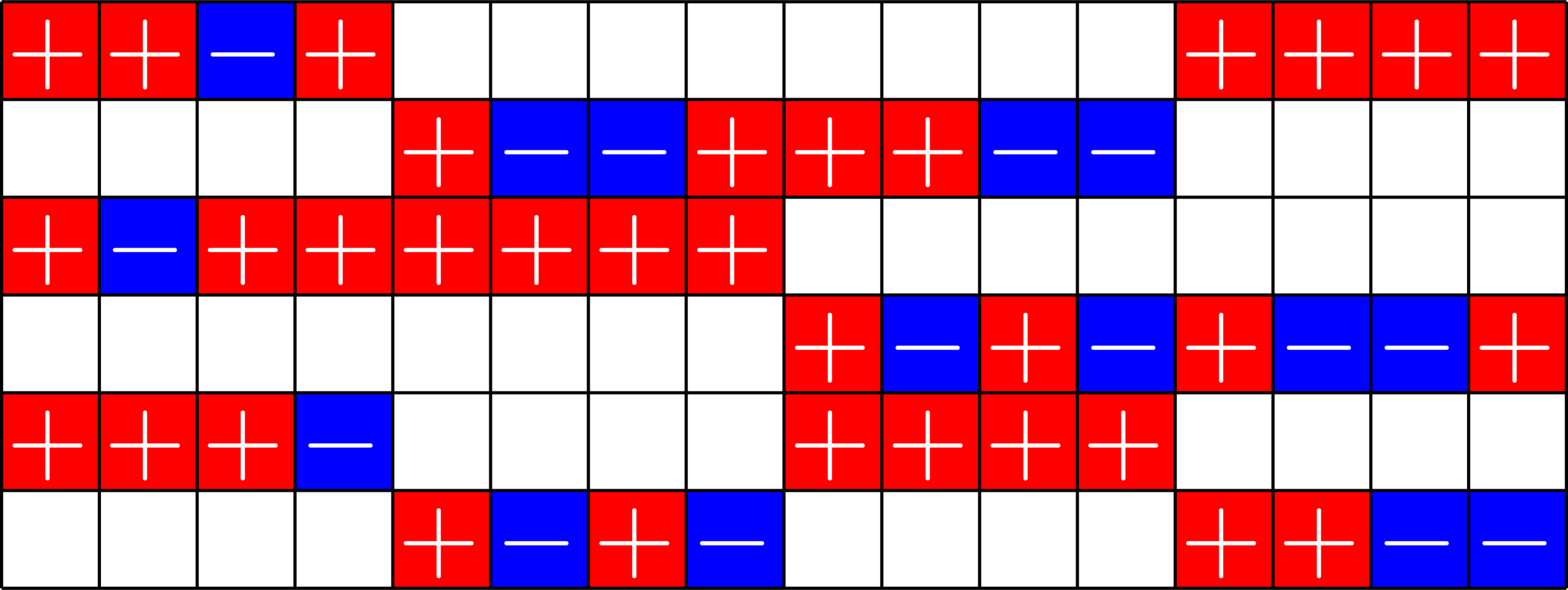
Real ETFs and Graphs

Given a real ETF \(\Phi\)
Normalize so that all dot products with the first vector are positive.
Look at the gram matrix \(\Phi^{\top}\Phi\)
Remove the first row and column and zero out the diagonal

Real ETFs and Graphs

Given a real ETF \(\Phi\)
Normalize so that all dot products with the first vector are positive.
Look at the gram matrix \(\Phi^{\top}\Phi\)
Remove the first row and column and zero out the diagonal
This is the Seidel adjacency matrix of a strongly regular graph

Real ETFs and Graphs

A. E. Brouwer maintains a table of known strongly regular graphs.

Our approach:

Real

ETFs

Combinatorial

designs

Strongly

regular graph

Construct

object

Certify

novelty

New Graphs!

Theorem (J, '21). If there exists an

\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),

then there exists a strongly regular graph with parameters:

\[v=h(2h+1),\quad k=h^2-1,\quad \lambda=\frac{1}{2}(h^2-4),\quad \mu = \frac{1}{2}h(h-1)\]

There exists a \(20\times 20\) Hadamard matrix, and hence an SRG(820,399,198,190), which is new!

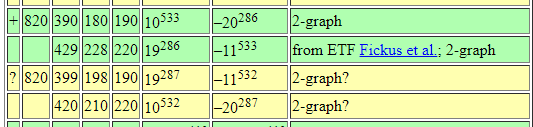
From Brouwer's table online:

Overall: Five new infinite families!

Roadmap for this talk

Compressed Sensing

Vectors that are "Spread out"

Equiangular tight frames

ETFs from groups

\(\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)

The design theory underneath

Real Flat ETFs

Some binary codes

Group divisible designs

ETFs and graphs

Single-pixel Camera

\(75\times 100\) image \(=7500\) pixels
We took \(4096\) measurements

Results

\(75\times 100\) image \(=7500\) pixels
We took \(4096\) measurements

Results

\(L^{1}\) Minimization Solution

\(L^{2}\) Minimization Solution

Thanks for your attention!

Questions?

Future work:

Subspaces that are "spread out"
Frames that saturate the Levenshtein bound
SRGs from finite geometries
Diagonals of self-adjoint operators