Finding optimal projective packings using a Newton-Kantorovich theorem
John Jasper
joint work w/ Joey Iverson, Dustin Mixon, and Staci Davis
AMS Fall Central Sectional
Special Session on Harmonic Analysis, Frame Theory, and Tilings

https://slides.com/johnjasper/amsstlouis/

The views expressed in this talk are those of the speaker and do not reflect the official policy
or position of the United States Air Force, Department of Defense, or the U.S. Government.
Support
Disclaimer
Results
Newton-Kantorovich:
"Close is good enough"
Outline
Optimal packings as zeros of polynomials
Packings
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\varphi_{i}^{\ast}\varphi_{j}^{}|.\]
Measuring how "spread out" vectors are
\[\mu(\Phi) = \cos(\theta)\]
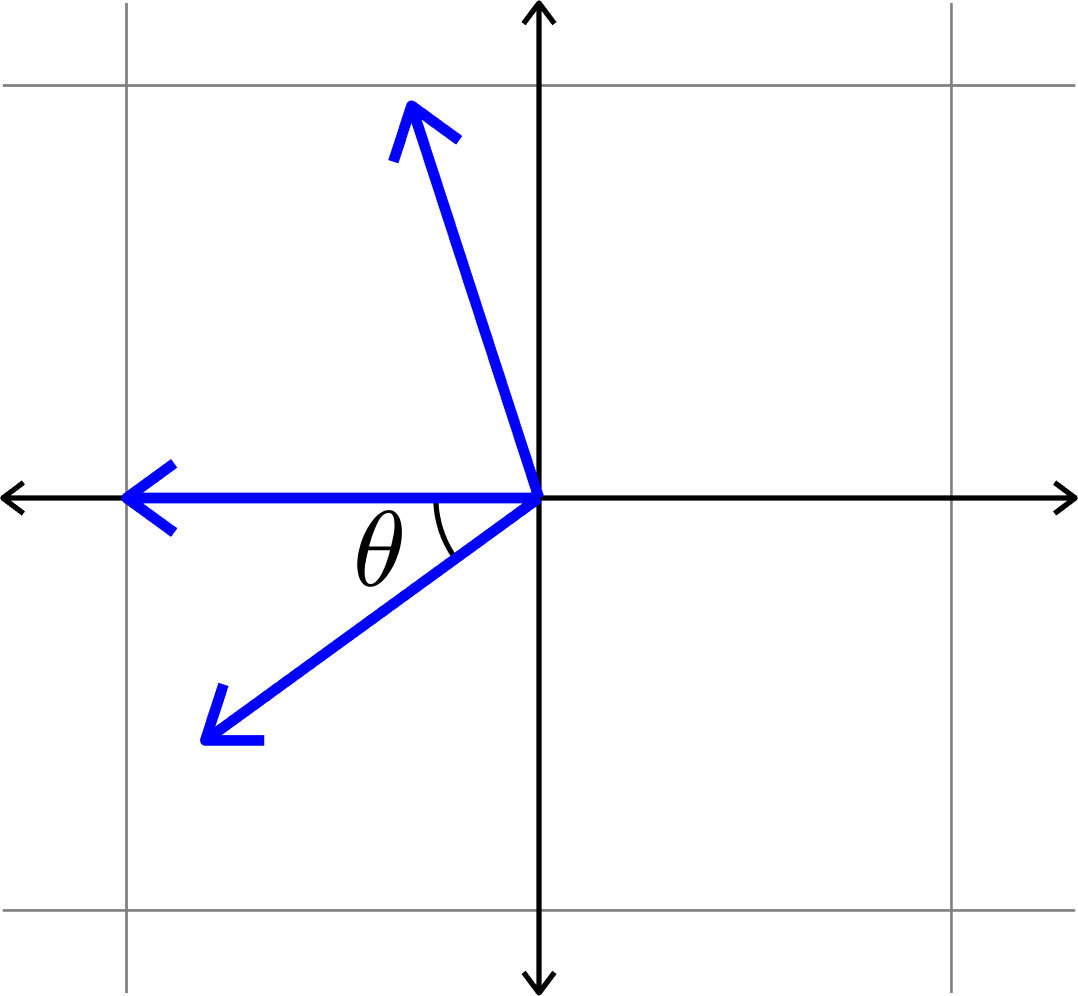
\(\mu(\Phi) = \cos(\theta)\)??
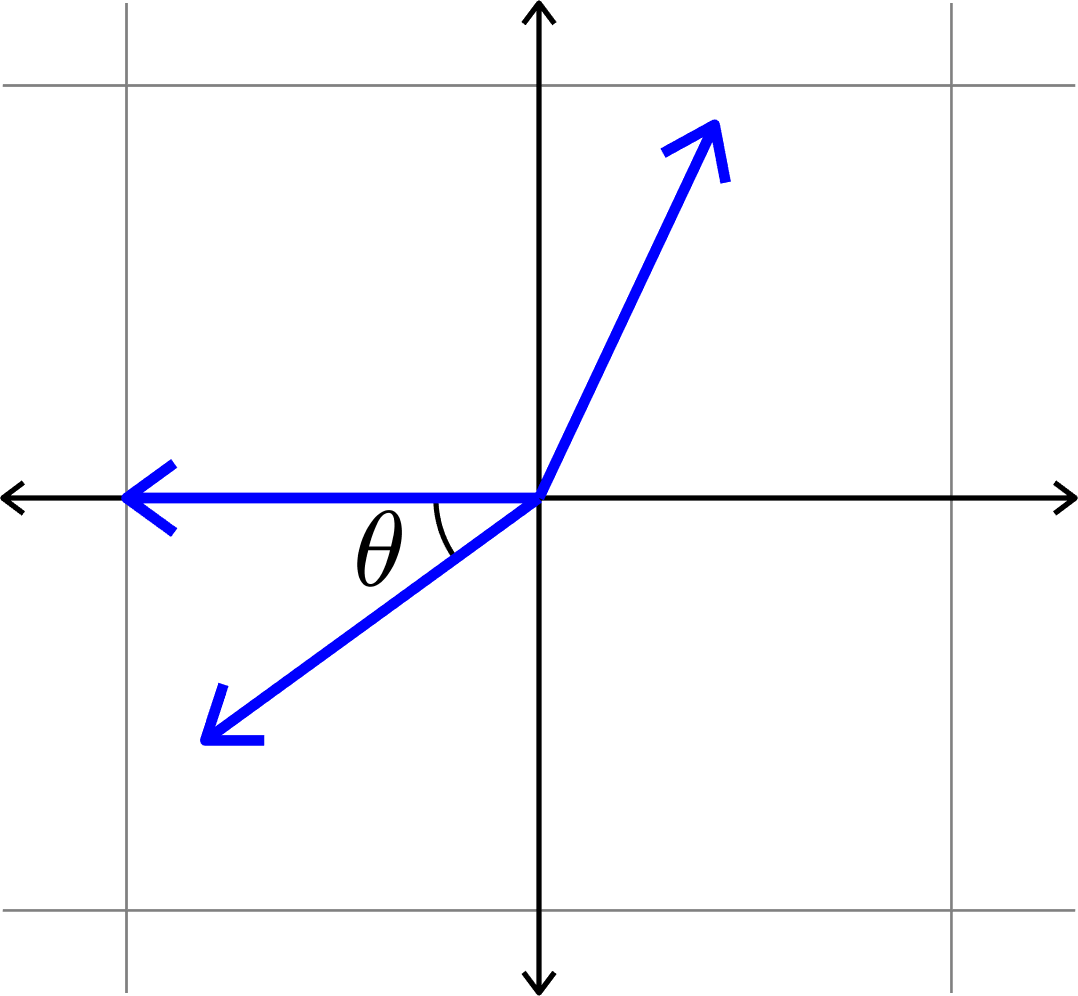
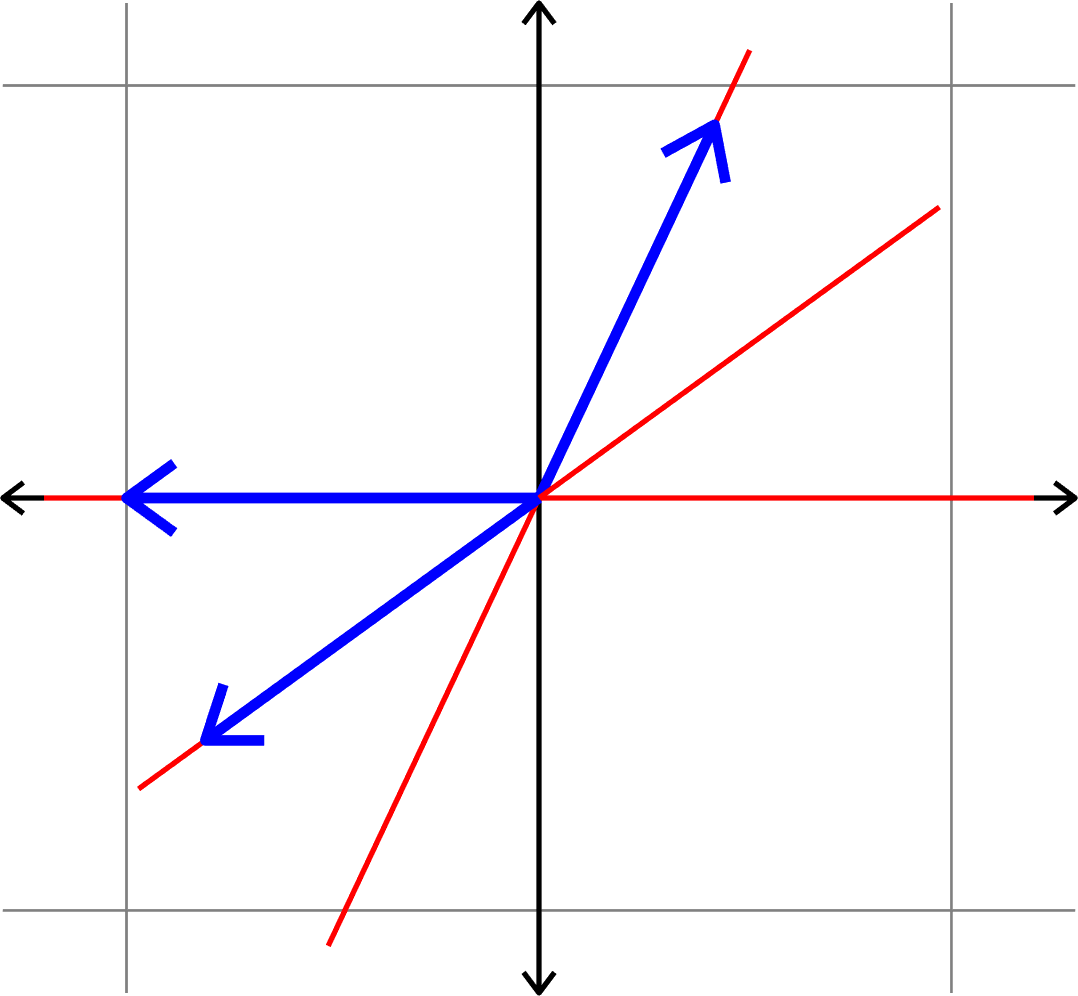
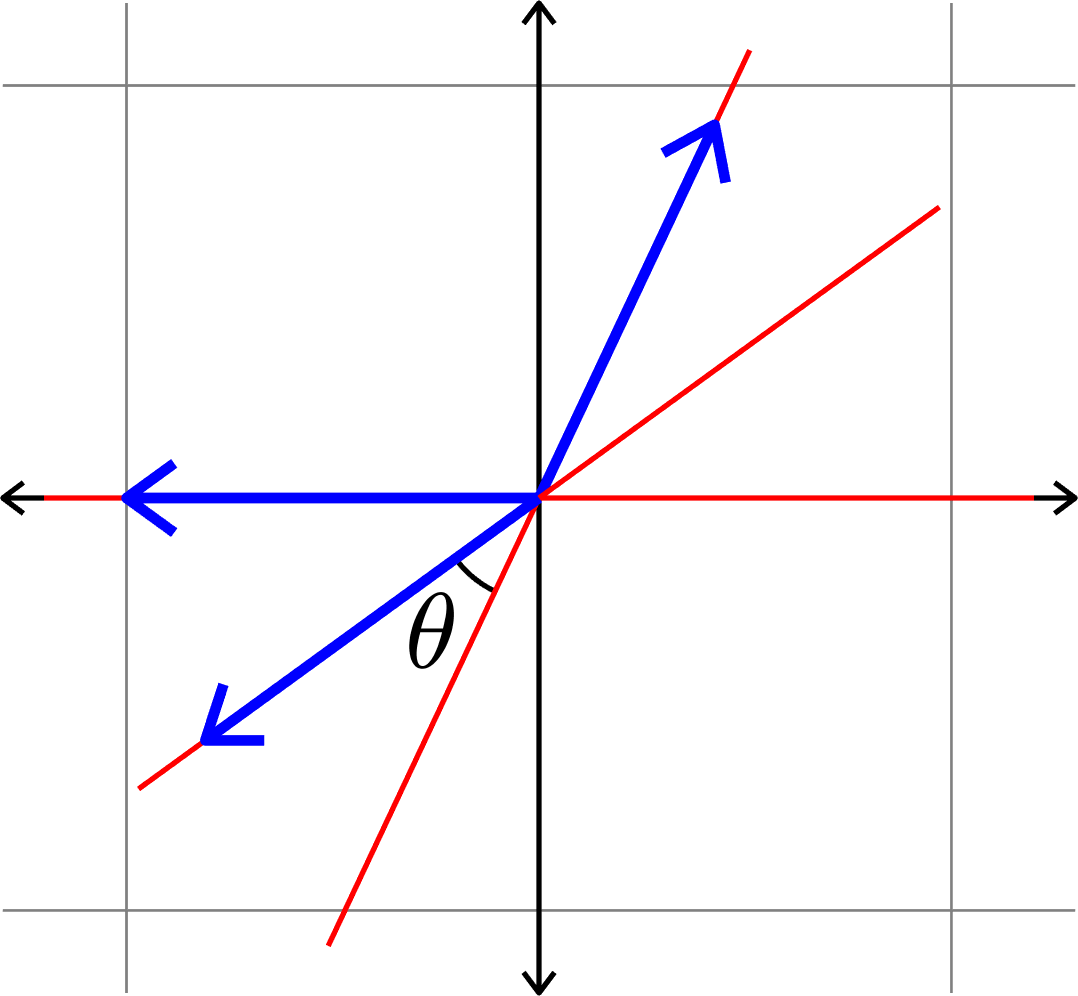
\(\mu(\Phi) = \cos(\theta)\)
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\varphi_{i}^{\ast}\varphi_{j}^{}|.\]
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\varphi_{i}^{\ast}\varphi_{j}^{}|.\]
Minimizing coherence
between vectors
\(\Updownarrow\)
Maximizing min. angle
between lines

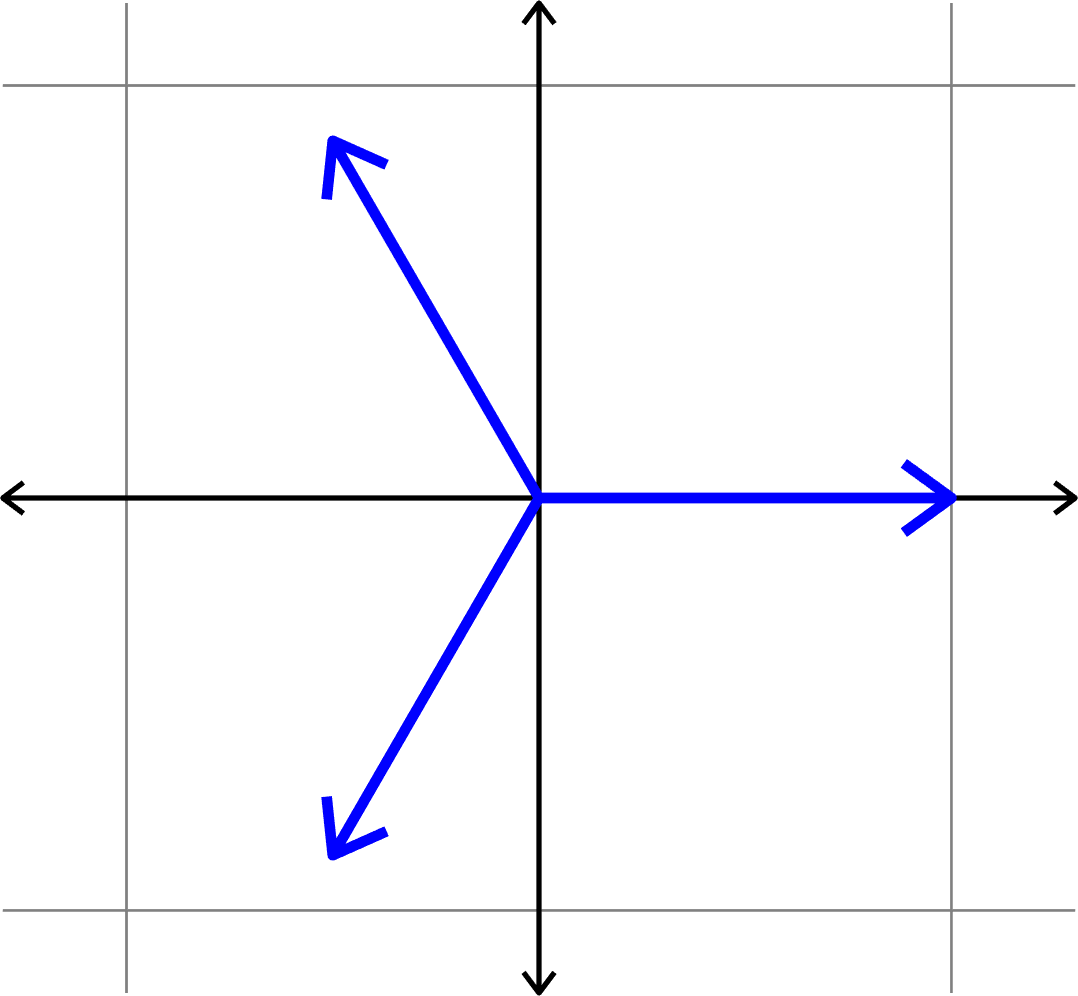
Example.
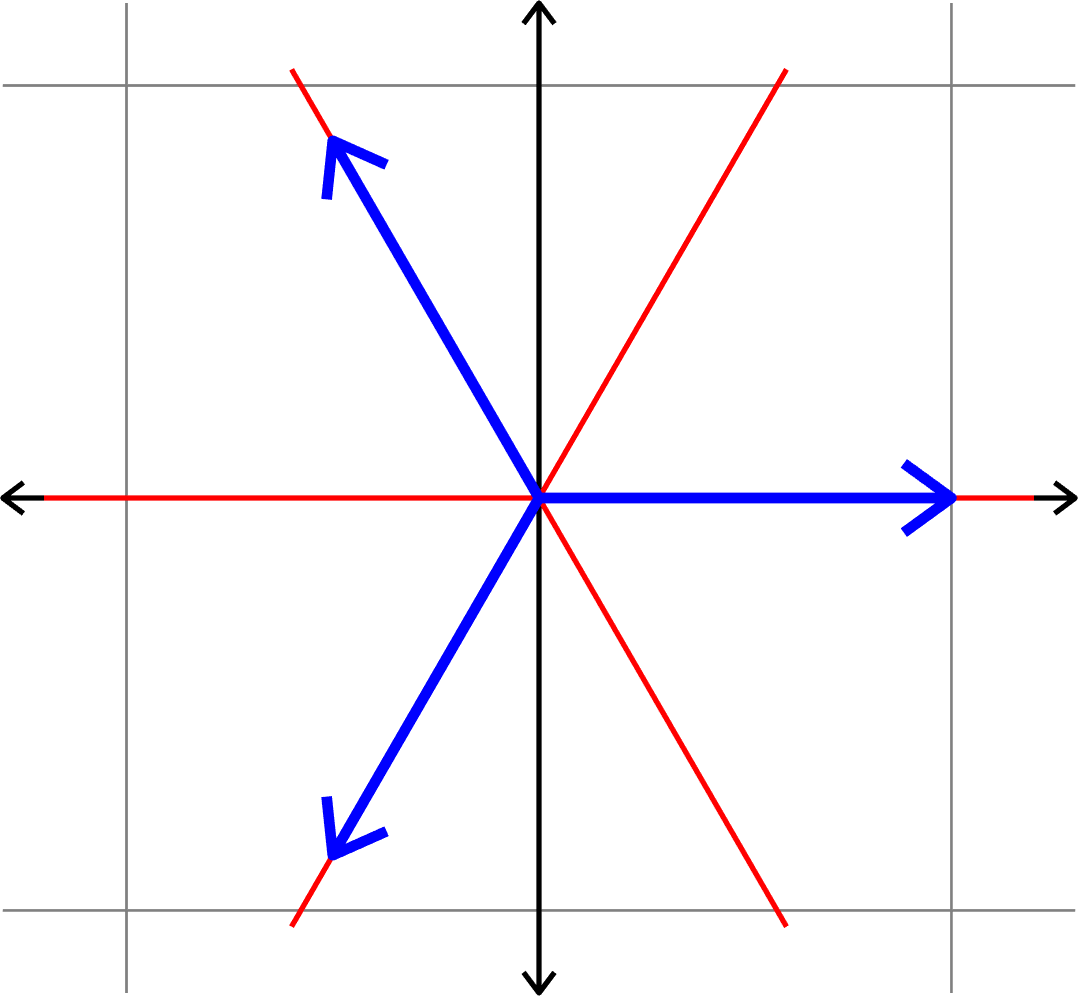
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}| \varphi_{i}^{\ast}\varphi_{j}|.\]
Given \((D,N)\), find \(\Phi = (\varphi_{i})_{i=1}^{N}\subset\mathbb{F}^{D}\) such that \(\mu(\Phi)\) is minimal.
Goal:
Vectors that are as spread out as possible
Theorem (the Welch bound). For unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{F}^D\)
\[\mu(\Phi)^{2} = \max_{i\neq j}|\varphi_{i}^{\ast}\varphi_{j}^{}|^{2}\geq \frac{N-D}{D(N-1)}.\]
Equality holds if and only if both:
- Tight: \(\displaystyle{\sum_{i=1}^{N}\varphi_{i}\varphi_{i}^{\ast} = \frac{N}{D}\mathbf{I}}.\)
- Equiangular: \(\displaystyle{|\varphi_{i}^{\ast}\varphi_{j}^{}|^{2} = \frac{N-D}{D(N-1)}\quad\text{for all }i\neq j.}\)
Welch bound equality \(\Longleftrightarrow\) equiangular tight frame (ETF)
The Short, Fat Matrix
Let \[\Phi = \big[\varphi_{1}\ \ \varphi_{2}\ \ \cdots\ \ \varphi_{N}\big]\in \mathbb{F}^{D\times N},\]
be a rank \(D\) matrix where each column \(\varphi_{n}\) has norm one.
Then \(\Phi\) is an ETF iff
(\(\mathbb{F} = \mathbb{C}\) or \(\mathbb{R}\))
\(\displaystyle{\sum_{i=1}^{N}\varphi_{i}\varphi_{i}^{\ast} = \frac{N}{D}\mathbf{I}}.\)
\(\displaystyle{|\varphi_{i}^{\ast}\varphi_{j}^{}|^{2} = \frac{N-D}{D(N-1)}}\) for \(i\neq j\)
Examples of equiangular tight frames
Example 2. Consider the (multiple of a) unitary matrix
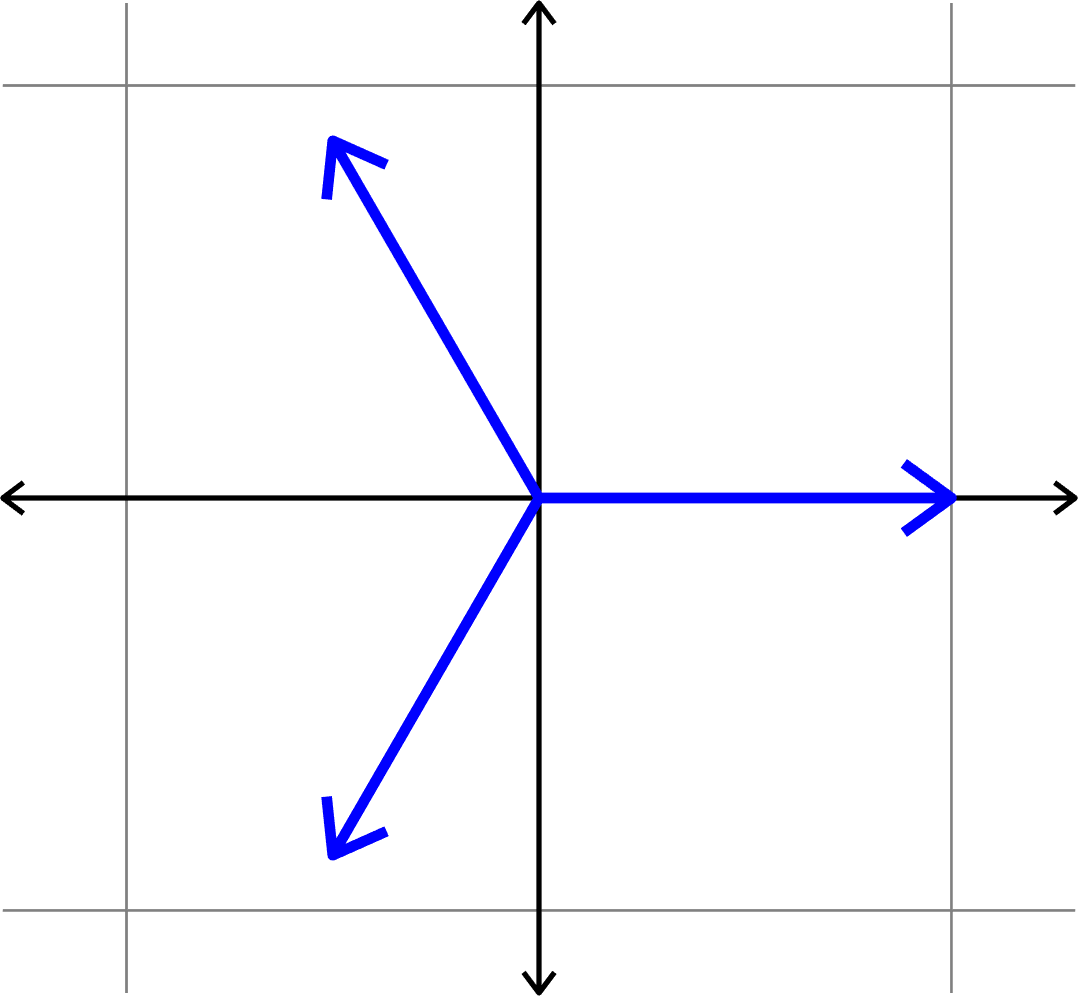
Example 1. Consider the (multiple of a) unitary matrix
\[\left[\begin{array}{rrrr}1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1\\ \sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
\[\left[\begin{array}{rrrr}\sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]

\[\frac{1}{\sqrt{2}}\]
\[\frac{1}{\sqrt{2}}\]
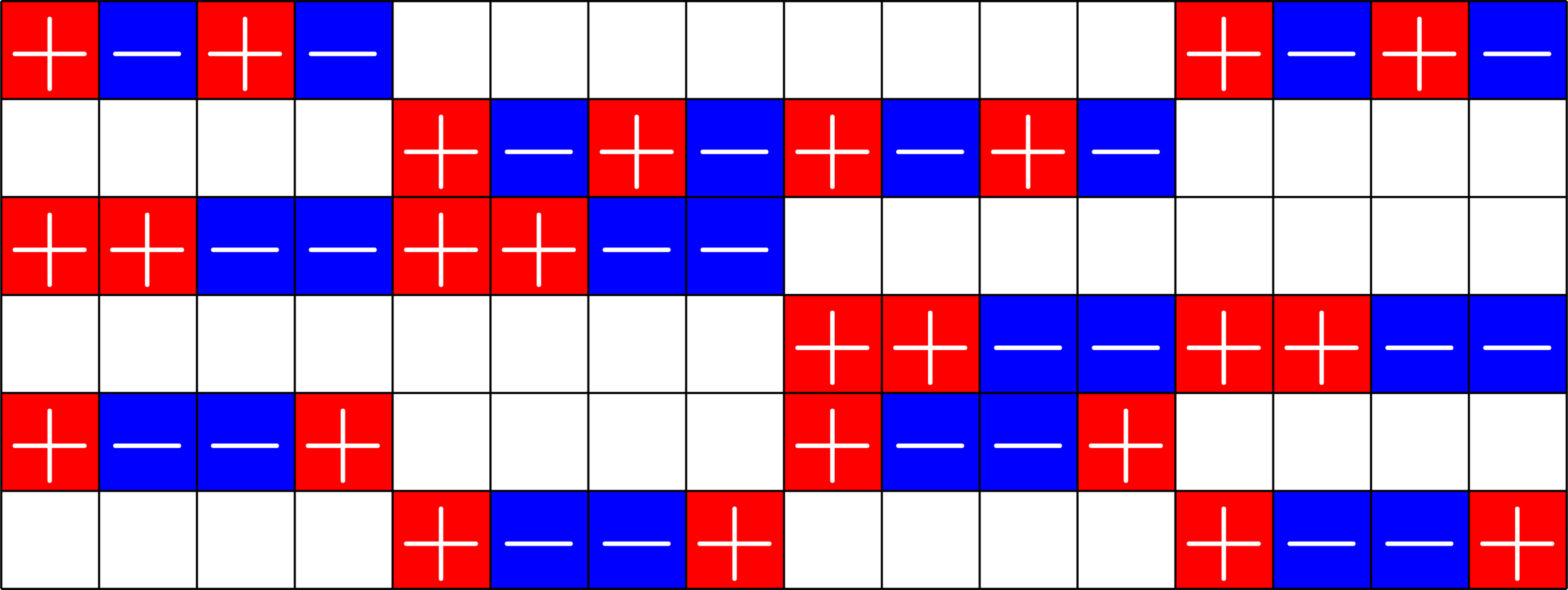
Example 3. \(\operatorname{ETF}(6,16)\)
- Rows are orthogonal
- Rows are equal norm
- all dot products of columns are \(\pm \frac{1}{3} = \pm\sqrt{\frac{16-6}{6(16-1)}}\)
\[\frac{1}{\sqrt{3}}\]
\[\Phi = \left[\begin{array}{cccccc} \varphi_{1,1} & \varphi_{1,2} & \varphi_{1,3} & \cdots & \cdots & \varphi_{1,N}\\ \varphi_{2,1} & \varphi_{2,2} & \varphi_{2,3} & \cdots & \cdots & \varphi_{2,N}\\ \varphi_{3,1} & \varphi_{3,2} & \varphi_{3,3} & \cdots & \cdots & \varphi_{3,N}\\ \vdots & \vdots & \vdots & \ddots & & \vdots\\ \varphi_{D,1} & \varphi_{D,2} & \varphi_{D,3} & \cdots & \cdots & \varphi_{D,N}\end{array}\right] \in\mathbb{R}^{D\times N}\]

Real, but we can do complex too
\(\displaystyle{\sum_{i=1}^{N}\varphi_{i}\varphi_{i}^{\top} = \frac{N}{D}\mathbf{I}}.\)
\(\displaystyle{(\varphi_{i}^{\ast}\varphi_{j}^{})^{2} = \frac{N-D}{D(N-1)}}\) for \(i\neq j\)
is an ETF iff
\[\Leftrightarrow\qquad\qquad\sum_{i=1}^{N}\varphi_{d,i}\varphi_{d',i} = \frac{N}{D}\delta_{d,d'}\ \text{for }d\neq d'\]
\[\Leftrightarrow\quad\sum_{d=1}^{D}\varphi_{d,i}\varphi_{d,j} = \frac{N-D}{D(N-1)}\ \text{for }i\neq j\]
It's a bunch of polynomials
\[\Phi = \left[\begin{array}{cccccc} \varphi_{1,1} & \varphi_{1,2} & \varphi_{1,3} & \cdots & \cdots & \varphi_{1,N}\\ \varphi_{2,1} & \varphi_{2,2} & \varphi_{2,3} & \cdots & \cdots & \varphi_{2,N}\\ \varphi_{3,1} & \varphi_{3,2} & \varphi_{3,3} & \cdots & \cdots & \varphi_{3,N}\\ \vdots & \vdots & \vdots & \ddots & & \vdots\\ \varphi_{D,1} & \varphi_{D,2} & \varphi_{D,3} & \cdots & \cdots & \varphi_{D,N}\end{array}\right] \in\mathbb{R}^{D\times N}\]
is an ETF iff
\[\sum_{i=1}^{N}\varphi_{d,i}\varphi_{d',i} = \frac{N}{D}\delta_{d,d'}\ \text{for }d\neq d'\]
\[\sum_{d=1}^{D}\varphi_{d,i}\varphi_{d,j} = \delta_{i,j}\ \text{for }i\neq j\]
It's a bunch of polynomials
Define polynomial map
\(f:\R^{A}\to\R^{B}\) where
\(f(\Phi)=0\ \Leftrightarrow\ \Phi\) is an ETF
Spread out subspaces
- \((\mathcal{U}_{n})_{n=1}^{N}\) be \(R\)-dim subspaces of \(\mathbb{F}^{D}\)
- \(\Phi_{n}\in\mathbb{F}^{D\times R}\) be an ONB for \(\mathcal{U}_{n}\)
- \(\Pi_{n}\) be proj. onto \(\mathcal{U}_{n}\)
Chordal distance:
\[d_{c}(\mathcal{U}_{i},\mathcal{U}_{j}) = 2^{-1/2}\|\Pi_{i} - \Pi_{j}\|_{\text{Fro}} = \sqrt{R - \|\Phi_{i}^{\ast}\Phi_{j}\|_{\text{Fro}}^{2}}.\]
Measure of "spread outness"
\[\min_{i\neq j}(d_{c}(\mathcal{U}_{i},\mathcal{U}_{j}))^2 = R - \max_{i\neq j}\|\Phi_{i}^{\ast}\Phi_{j}\|_{\text{Fro}}^{2}.\]
\(\Leftrightarrow\) \(\displaystyle{\min_{i\neq j} d_{c}(\mathcal{U}_{i},\mathcal{U}_{j})}\) large \(\Leftrightarrow\) \(\displaystyle{\max_{i\neq j}\|\Phi_{i}^{\ast}\Phi_{j}\|^{2}_{\text{Fro}}}\) small
Subspaces spread out
Subspaces as spread out as possible
Theorem (the Welch bound). Suppose
Equality holds if and only if both:
- Tight: \(\displaystyle{\sum_{n=1}^{N}\Phi_{n}\Phi_{n}^{\ast} = \frac{NR}{D}\mathbf{I}}\)
- Equichordal : \(\displaystyle{\|\Phi_{i}^{\ast}\Phi_{j}\|_{\text{Fro}}^{2} =\frac{R(NR-D)}{D(N-1)}\quad\text{for all }i\neq j.}\)
Simplex bound equality \(\Longleftrightarrow\) equichordal tight fusion frame (ECTFF)
- \((\mathcal{U}_{n})_{n=1}^{N}\) be \(R\)-dim subspaces of \(\mathbb{F}^{D}\)
- \(\Phi_{n} \) be an ONB for \(\mathcal{U}_{n}\)
Then, \[\max_{i\neq j}\|\Phi_{i}^{\ast}\Phi_{j}\|^{2}_{\text{Fro}}\geq \frac{R(NR-D)}{D(N-1)}\]

The Short, Fat Matrix
Let \[\Phi = \big[\ \Phi_{1}\ \vert\ \Phi_{2}\ \vert\ \cdots\ \vert\ \Phi_{N}\big]\in \big(\mathbb{F}^{D\times R}\big)^{1\times N},\]
Where \(\Phi_{n}\) is an orthonormal basis for \(\mathcal{U}_{n}\)
Then \(\Phi\) is an ECTFF iff
\(\displaystyle{\sum_{n=1}^{N}\Phi_{n}\Phi_{n}^{\ast} = \frac{NR}{D}\mathbf{I}}\)
\(\displaystyle{\|\Phi_{i}^{\ast}\Phi_{j}\|_{\text{Fro}}^{2} =\frac{R(NR-D)}{D(N-1)}\quad\text{for }i\neq j.}\)


Example. ECTFF w/ 10 subspaces of \(\R^{5}\), each of dimension \(5\).
\(\Phi\)
Examples of and ECTFF
It's a bunch of polynomials
is an ECTFF iff
\[\sum_{n=1}^{N}\sum_{r=1}^{R}\varphi_{d,r,n}\varphi_{d',r,n} = \frac{NR}{D}\delta_{d,d'}\quad \text{for all }d,d'\]
\[\sum_{r=1}^{R}\sum_{r'=1}^{R}\left(\sum_{d=1}^{D}\varphi_{d,r,n}\varphi_{d,r',n'}\right)^{2} = \frac{R(NR-D)}{D(N-1)}\quad \text{for } n\neq n'\]
\[\Phi = \big[\ \Phi_{1}\ \vert\ \Phi_{2}\ \vert\ \cdots\ \vert\ \Phi_{N}\big],\]
\[\left[\begin{array}{ccc|ccc|c|ccc} \varphi_{1,1,1} & \cdots & \varphi_{1,R,1} & \varphi_{1,1,2} & \cdots & \varphi_{1,R,2} & \cdots & \varphi_{1,1,N} & \cdots & \varphi_{1,R,N}\\[1ex] \varphi_{2,1,1} & \cdots & \varphi_{2,R,1} & \varphi_{2,1,2} & \cdots & \varphi_{2,R,2} & \cdots & \varphi_{2,1,N} & \cdots & \varphi_{2,R,N}\\ \vdots & & \vdots & \vdots & & \vdots & & \vdots & & \vdots\\ \varphi_{D,1,1} & \cdots & \varphi_{D,R,1} & \varphi_{D,1,2} & \cdots & \varphi_{D,R,2} & \cdots & \varphi_{D,1,N} & \cdots & \varphi_{D,R,N} \end{array}\right] \]
\[=\]
\(\displaystyle{\sum_{n=1}^{N}\Phi_{n}\Phi_{n}^{\ast} = \frac{NR}{D}\mathbf{I}}\)
\(\Phi_{n}^{\ast}\Phi^{}_{n} = \mathbf{I}_{R}\) for each \(n\)
\(\displaystyle{\|\Phi_{n}^{\ast}\Phi_{n'}\|_{\text{Fro}}^{2} =\frac{R(NR-D)}{D(N-1)}\quad\text{for }n\neq n'.}\)
\[\sum_{d=1}^{D}\varphi_{d,n,r}\varphi_{d,n,r'} = \delta_{r,r'}\text{for all }n,r,r'\]
It's a bunch of polynomials
is an ETF iff
\[\sum_{n=1}^{N}\sum_{r=1}^{R}\varphi_{d,r,n}\varphi_{d',r,n} = \frac{NR}{D}\delta_{d,d'}\quad \text{for all }d,d'\]
\[\sum_{r=1}^{R}\sum_{r'=1}^{R}\left(\sum_{d=1}^{D}\varphi_{d,r,n}\varphi_{d,r',n'}\right)^{2} = \frac{R(NR-D)}{D(N-1)}\quad \text{for } n\neq n'\]
\[\Phi = \big[\ \Phi_{1}\ \vert\ \Phi_{2}\ \vert\ \cdots\ \vert\ \Phi_{N}\big],\]
\[\left[\begin{array}{ccc|ccc|c|ccc} \varphi_{1,1,1} & \cdots & \varphi_{1,R,1} & \varphi_{1,1,2} & \cdots & \varphi_{1,R,2} & \cdots & \varphi_{1,1,N} & \cdots & \varphi_{1,R,N}\\[1ex] \varphi_{2,1,1} & \cdots & \varphi_{2,R,1} & \varphi_{2,1,2} & \cdots & \varphi_{2,R,2} & \cdots & \varphi_{2,1,N} & \cdots & \varphi_{2,R,N}\\ \vdots & & \vdots & \vdots & & \vdots & & \vdots & & \vdots\\ \varphi_{D,1,1} & \cdots & \varphi_{D,R,1} & \varphi_{D,1,2} & \cdots & \varphi_{D,R,2} & \cdots & \varphi_{D,1,N} & \cdots & \varphi_{D,R,N} \end{array}\right] \]
\[=\]
\[\sum_{d=1}^{D}\varphi_{d,n,r}\varphi_{d,n,r'} = \delta_{r,r'}\text{for all }n,r,r'\]
Define polynomial map
\(f:\R^{A}\to\R^{B}\) where
\(f(\Phi)=0\ \Leftrightarrow\ \Phi\) is an ECTFF
What's close enough?
Theorem (Newton-Kantorovich) [Cohn, Kumar, Minton '16].
- \(V\) and \(W\) fin. dim. normed spaces
- Fix \(x_{0}\in V\) and \(\varepsilon>0\)
- \(f:B(x_{0},\varepsilon)\to W\) is \(C^{1}\)
If \(\exists\) linear \(T:W\to V\) such that
\[\|\mathbf{I}_{W} - Df(x)T\|<1-\frac{\|T\|\|f(x_{0})\|}{\varepsilon}\quad\text{for all }x\in B(x_{0},\varepsilon),\]
then \(\exists\, x^{\ast}\in B(x_{0},\varepsilon)\) such that \(f(x^{\ast})=0\).
Plan:
- Find \(\tilde{x}_{0}\) s.t. \(f(\tilde{x}_{0})\approx 0\).
- \(\tilde{T} = \) pseudo inverse of Jacobian \(Df(\tilde{x}_{0})\)
- Round both to rationals \(x_{0}\) and \(T\).
- Find \(\varepsilon\) s.t. (\(\ast\)) holds. (Check this in computer with exact arithmetic.)
Problems!
How to compute \(\|T\|\)??
How to check (\(\ast\)) for \(\infty\) many \(x\)'s??
(\(\ast\))
Computing \(\|T\|\) exactly
Proposition. If \(T:\mathbb{R}^{C}\to\mathbb{R}^{D}\) is linear, both spaces have \(\ell^{\infty}\) norm, then the operator norm
\[\|T\|_{\infty\to\infty} = \max\{\|T_{i}\|_{1} : T_{i}\text{ is a col. of }T\}.\]
Entries of \(T\) in \(\mathbb{Q}\) \(\ \ \implies\ \ \) Can compute\(\|T\|_{\infty\to\infty}\) exactly
Controlling the Jacobian
Theorem [Cohn, Kumar, Minton '16]. Suppose \(\varepsilon>0\), \(C\geq D\), \(x_{0}\in\R^{C}\)
- \(f:\R^{C}\to\R^{D}\) polynomial map of total degree \(d\)
- \(\eta = \max\{1,\|x_{0}\|_{\infty}+\varepsilon\}\)
Then, \(\forall\, x\in B(x_{0},\varepsilon)\)
\[\|Df(x) - Df(x_{0})\|_{\infty\to\infty}\leq |f|d(d-1)\varepsilon\eta^{d-2}.\]
Corollary. Suppose \(f\) is as above. If there exists \(\varepsilon>0\), \(x_{0}\in \R^{C}\), and linear \(T:\R^{D}\to \R^{C}\) such that
\[\|Df(x_0) T - \mathbf{I}\|_{\infty\to\infty}+ \varepsilon|f|d(d-1)\eta^{d-2}\|T\| _{\infty\to\infty}< 1-\frac{\|T\|_{\infty\to\infty} \|f(x_0)\|}{\varepsilon},\]
then \(\exists\,x^{\ast}\) such that \(f(x^{\ast})=0\).
Close enough!
\[\begin{array}{|c|c|c|} \hline D & R & N\\ \hline 4 & 2 & 4,5-6 \\ 5 & 2 & 5-10 \\ 6 & 2 & 5-14 \\ 6 & 3 & 5-16 \\ 7 & 2 & 6-17 \\ 7 & 3 & 5-22 \\ 8 & 2 & 6-21 \\ 8 & 3 & 5-28 \\ 8 & 4 & 5-30 \\ 9 & 2 & 7-24 \\ 9 & 3 & 5-34 \\ 9 & 4 & 5-38 \\ 10 & 2 & 8-27 \\ 10 & 3 & 5-40 \\ 10 & 4 & 5-46 \\ 10 & 5 & 5-48 \\ \hline \end{array}\]
Theorem. For each entry in the table
\(\exists\) ECTFF with \(N\) subpaces, each with dimension \(R\) in \(\R^{D}\).
Results on Subspaces
For each \((D,R)\), these are the expected \(N\)'s.
\(\# \)constraints\(\,<\#\)variables
Redundancy Two ETFs

\(d\)'s in boxes due to Fallon, Iverson, J, and Mixon
\(2\)-Circulant
The \(11\times 22\) ETF found by Fallon and Iverson:
Real part
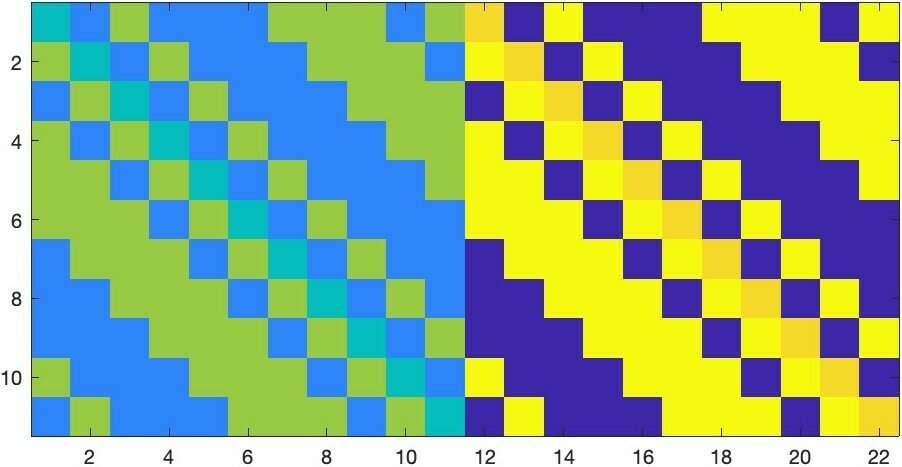
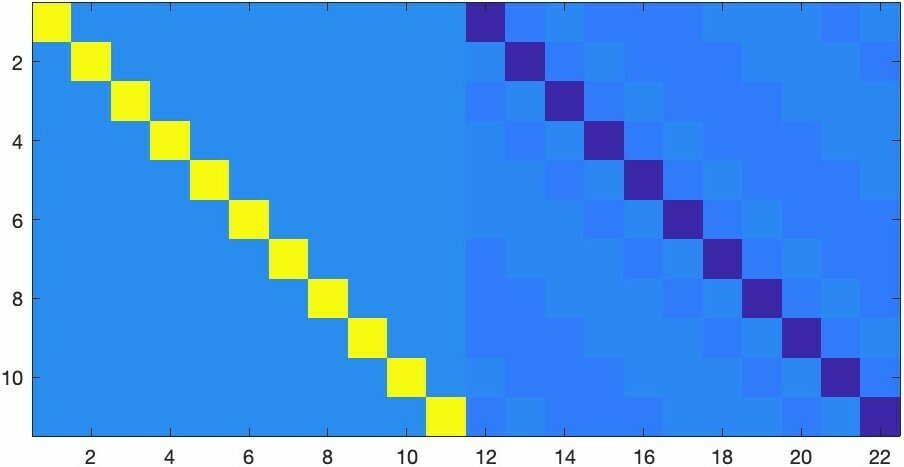
Imaginary part
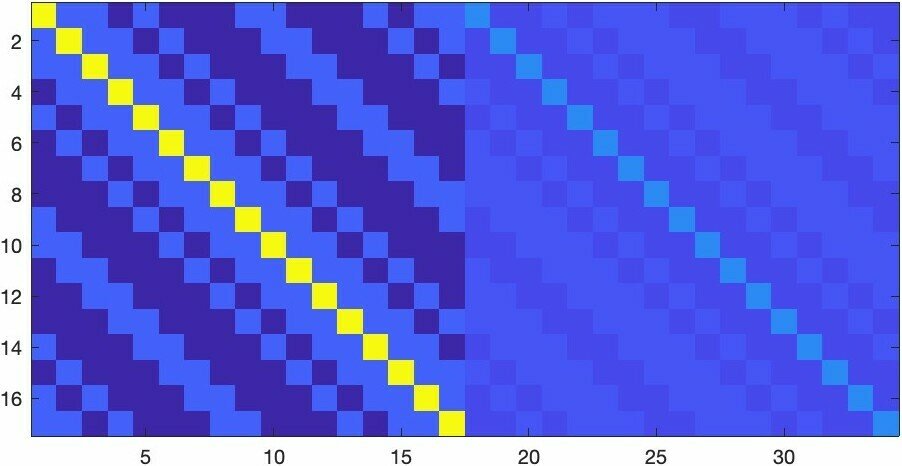
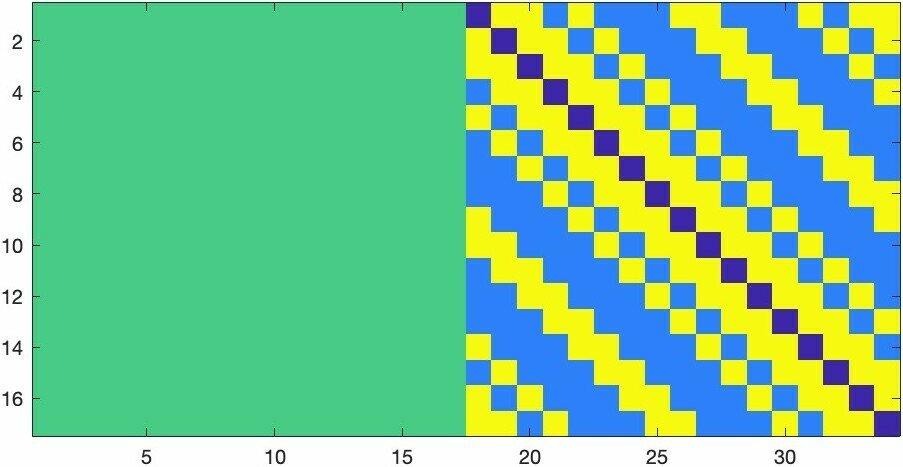
Real part
Imaginary part
The \(17\times 34\) ETF found by Iverson, J, Mixon:

Known exact 2-circulants
Conjecture (strong(ish) \(d\times 2d\) conjecture) [Iverson, J, Mixon]. For each \(d\), there exists a 2-circulant \(d\times 2d\) ETF.

Full conjecture gives dim. of manifold
Theorem [Iverson, J, Mixon]. The strong \(d\times 2d\) conjecture holds for \(d\leq 162\).
\[C_{\mathbf{x}} = \left[\begin{array}{ccccc} x_{0} & x_{d-1} & x_{d-2} & \cdots & x_{1}\\ x_{1} & x_{0} & x_{d-1} & \cdots & x_{2}\\ x_{2} & x_{1} & x_{0} & \cdots & x_{3}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{d-1} & x_{d-2} & x_{d-3} & \cdots & x_{0} \end{array}\right]\]
For \(\mathbf{x}\in \mathbb{C}^{d}\),
We want \(\mathbf{x},\mathbf{y}\in\mathbb{C}^{d}\) such that \(\Phi = [C_{\mathbf{x}}\ \ C_{\mathbf{y}}]\) is an ETF.
Make a polynomial map \(f\) such that \(f(\mathbf{x},\mathbf{y})=0\ \Leftrightarrow [C_{\mathbf{x}}\ \ C_{\mathbf{y}}]\) is an ETF.
Apply Newton-Kantorovich to \(f\).
Thanks!
