Consider the initial value problem:
\[y'(t) = ty(t),\qquad y(0) = 1.\]
Suppose \(\gamma\) is a solution on \([0,1/2]\), then we could use the fundamental theorem of calculus to see that
\[\gamma(t) = 1 + \int_{0}^{t}s\gamma(s)\,ds\]
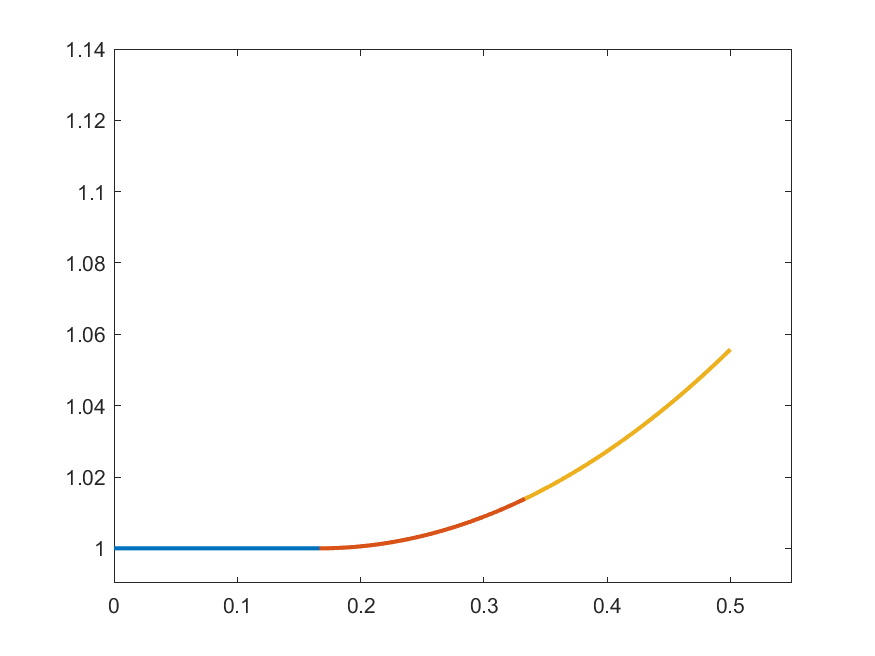
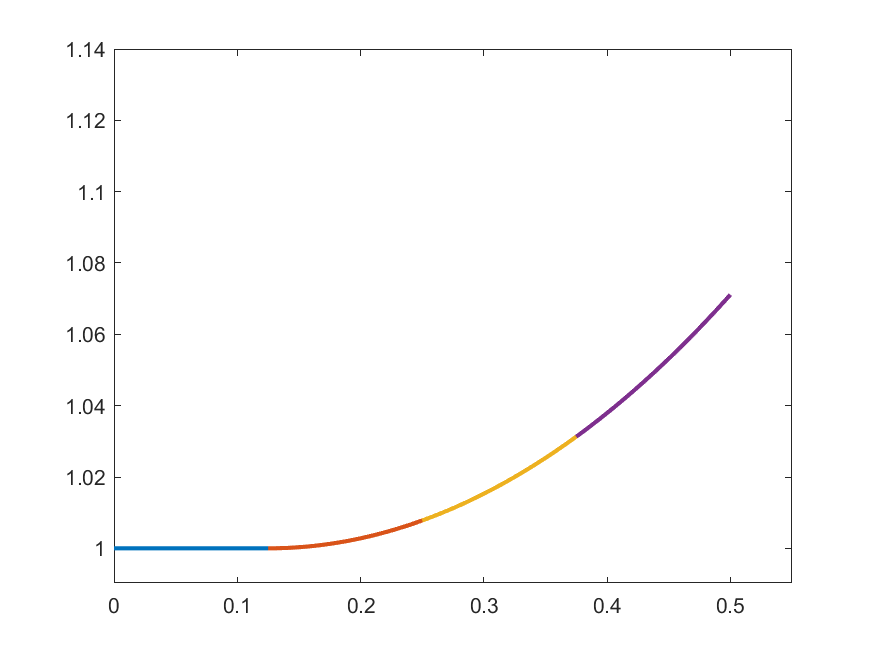
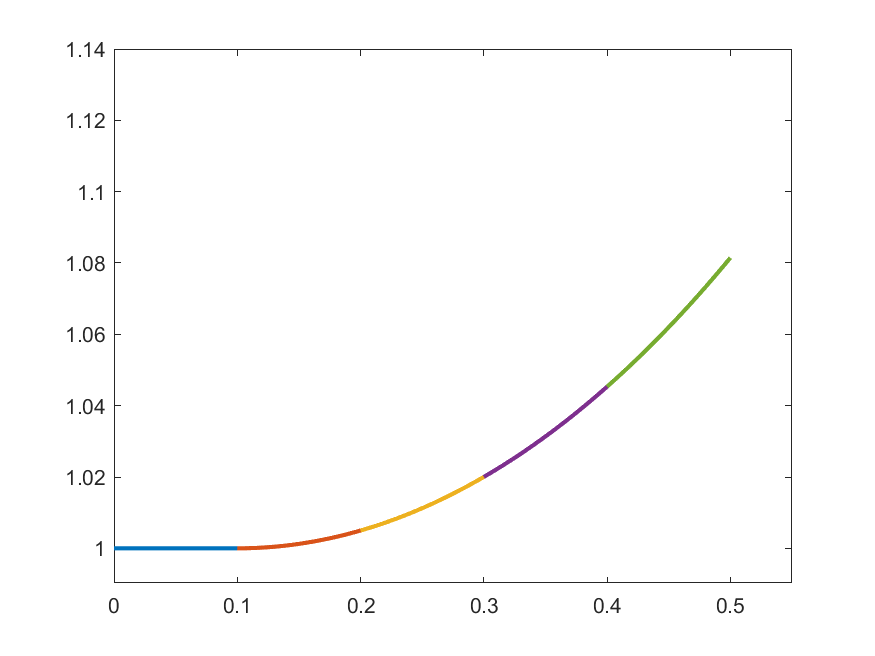
The idea in Peano is to find an approximate form of \((\ast)\) which we can solve: For each \(k\in\N\) set
\[\gamma_{k}(t) = 1 \quad\text{for }t\in\left[0,\frac{1}{2k}\right]\]
\((\ast)\)
and
\[\gamma_{k}(t) = 1+\int_{0}^{t-\frac{1}{2k}}s\gamma_{k}(s)\,ds\quad\text{for }t\in\left(\frac{1}{2k},\frac{1}{2}\right]\]
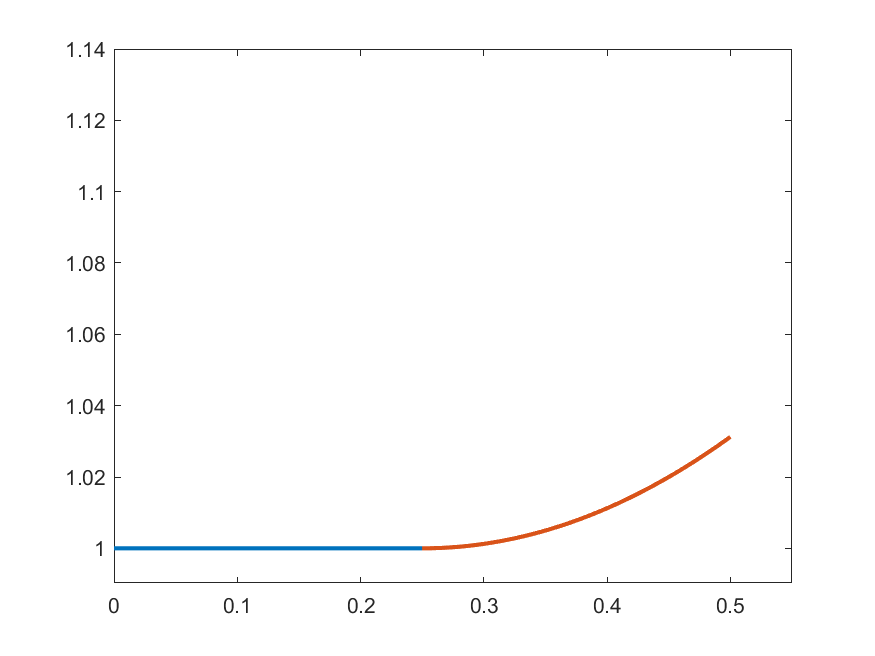
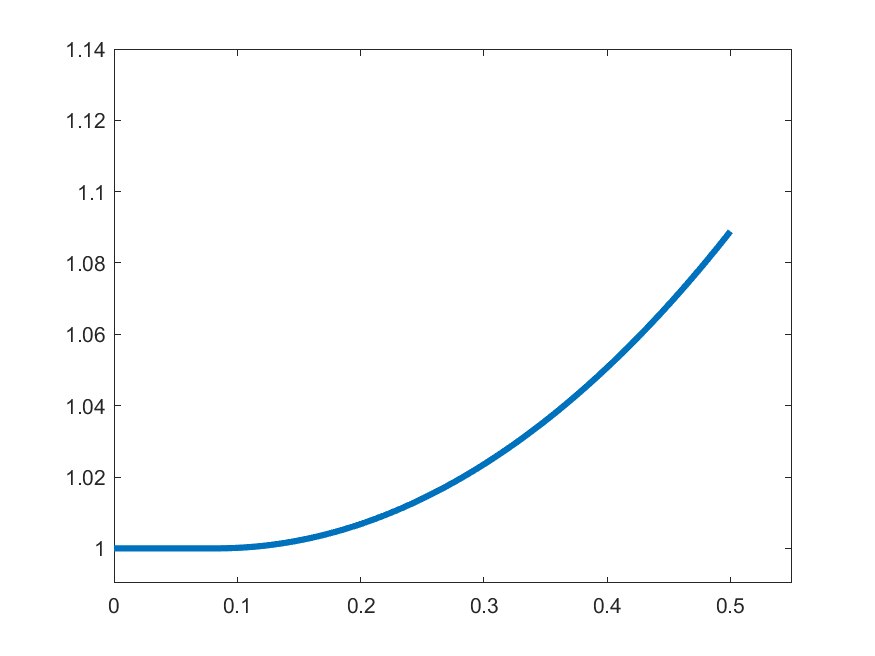
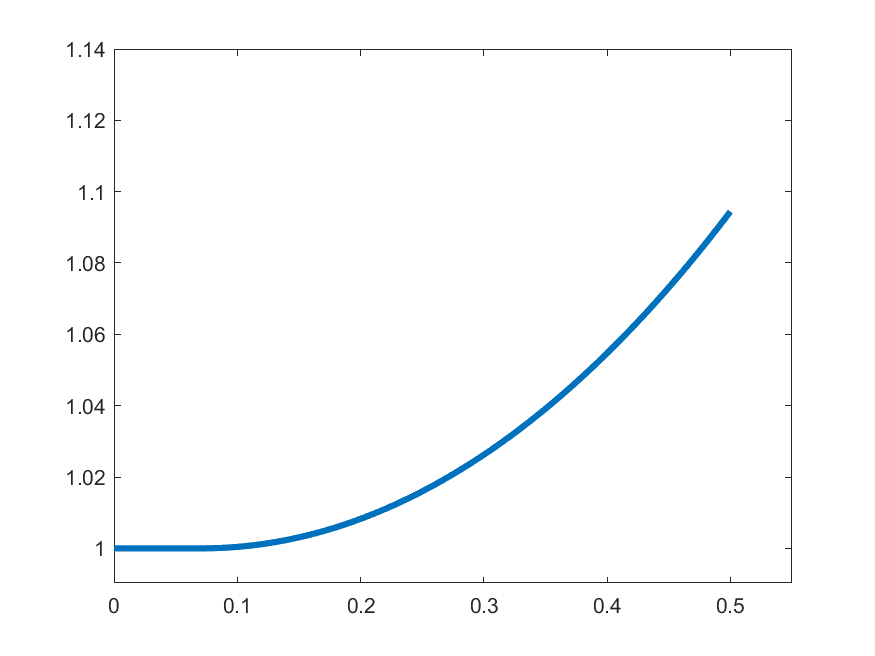
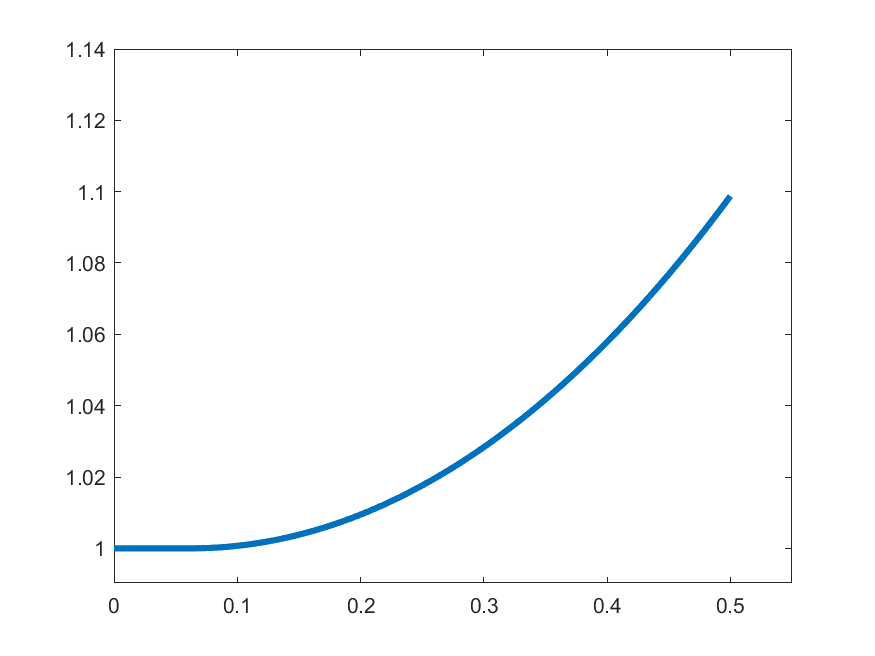

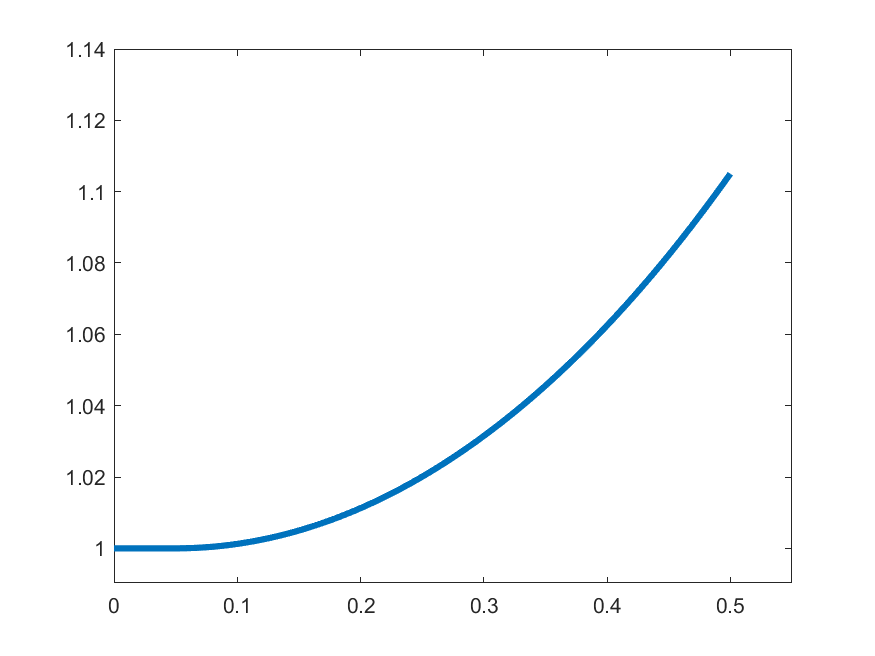
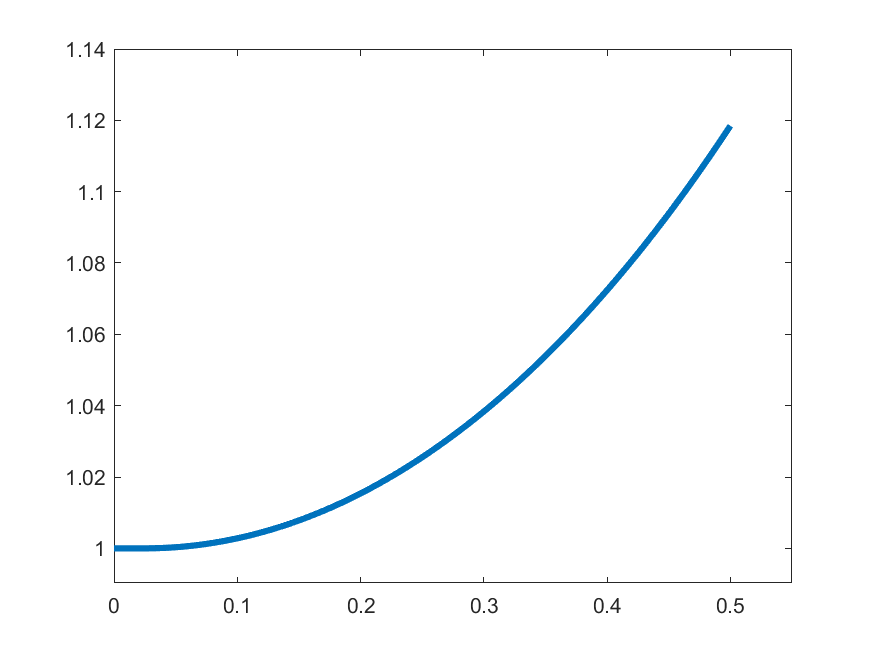
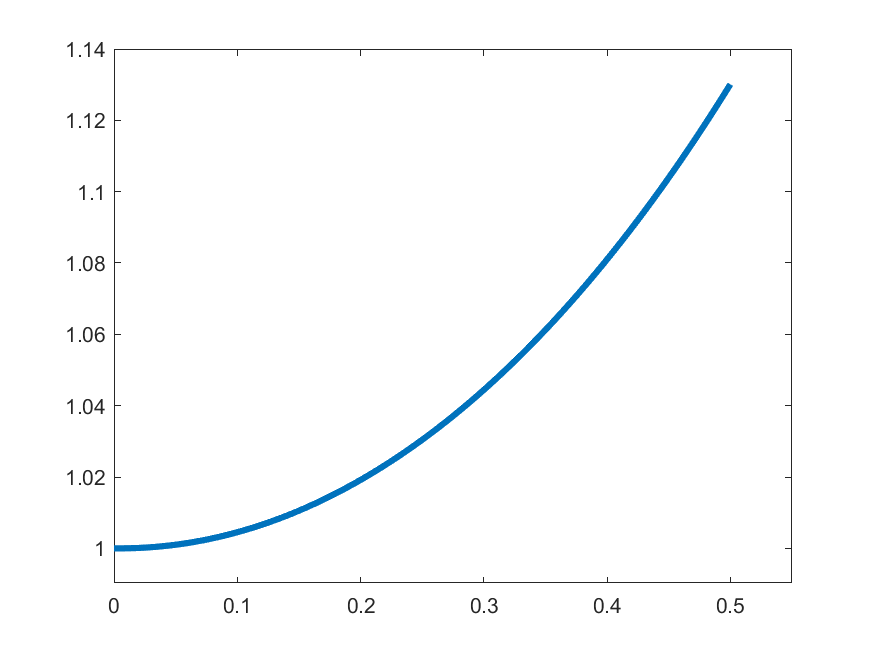
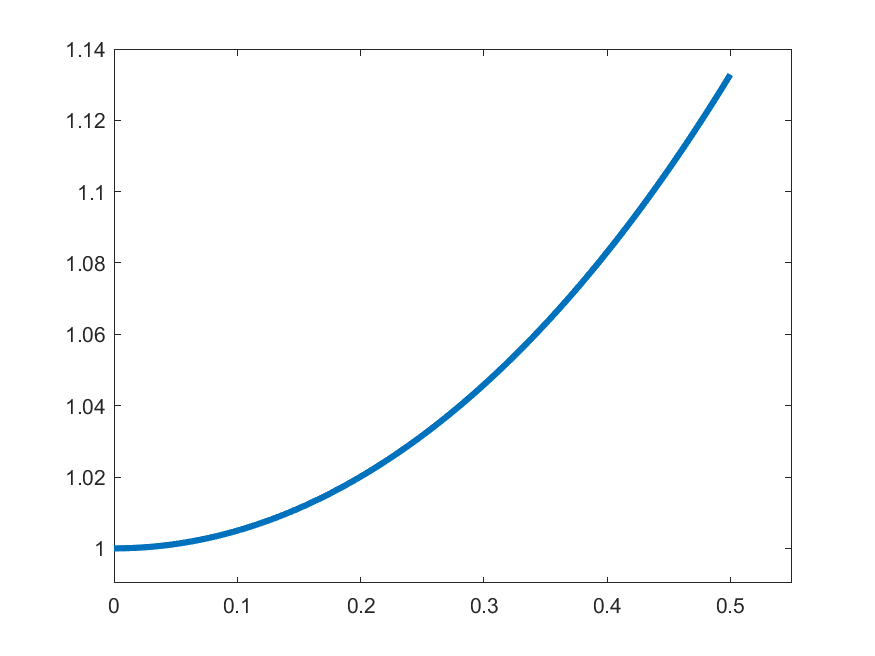
\(k=2\)
\(k=3\)
\(k=4\)
\(k=5\)
\(k=6\)
\(k=7\)
\(k=8\)
\(k=9\)
\(k=10\)
\(k=20\)
\(k=100\)
\(k=1000\)
\[\gamma_{k}(t) =\begin{cases}1 & t\in\left[0,\frac{1}{2k}\right]\\ \displaystyle{1+\int_{0}^{t-\frac{1}{2k}}s\gamma_{k}(s)\,ds} & t\in\left(\frac{1}{2k},\frac{1}{2}\right]\end{cases}\]
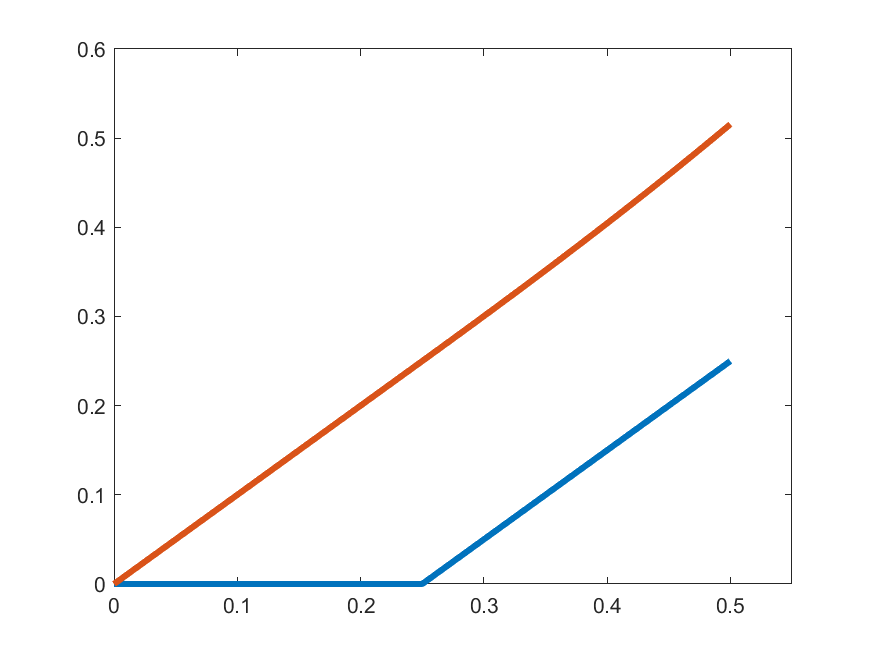
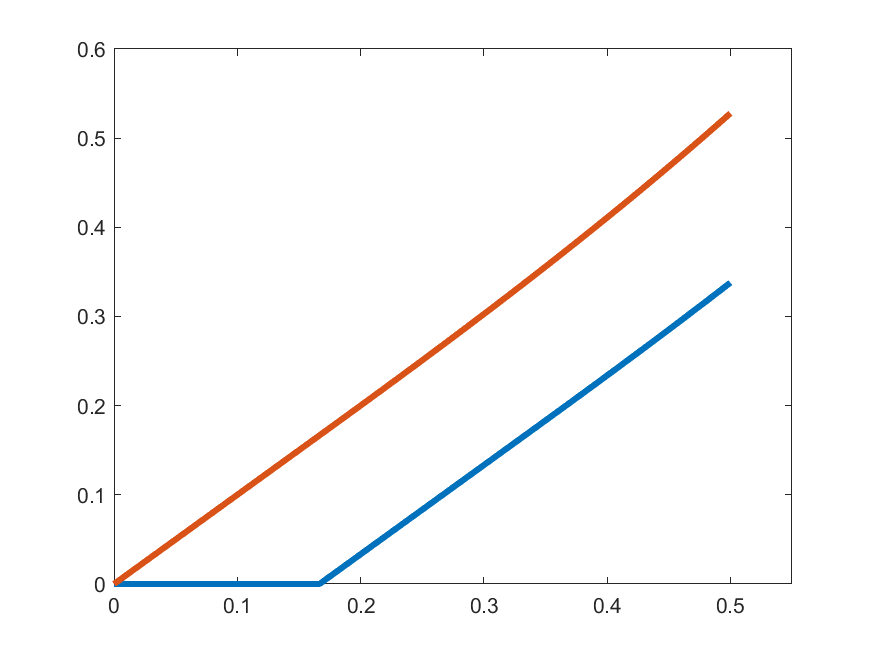
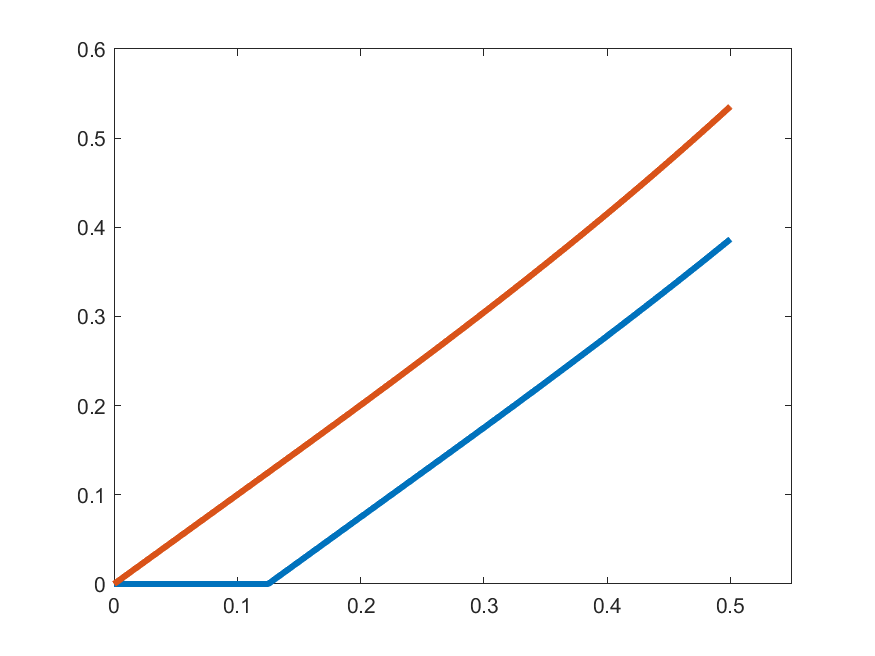
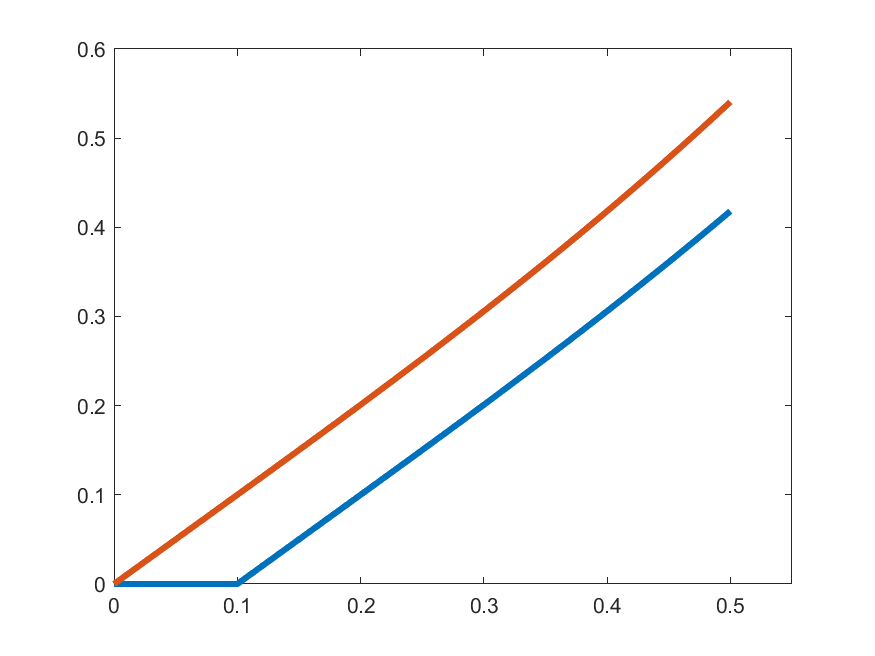
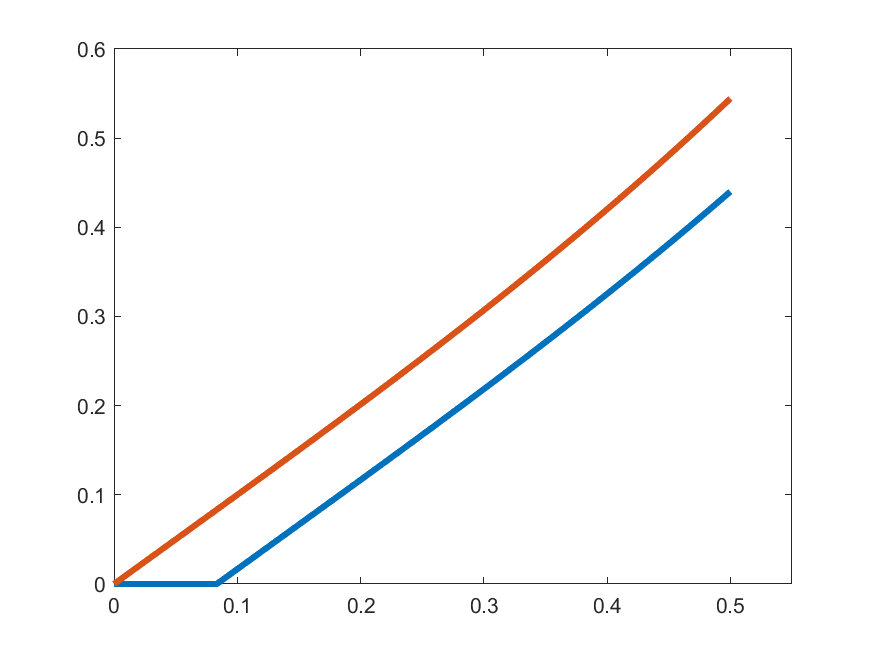
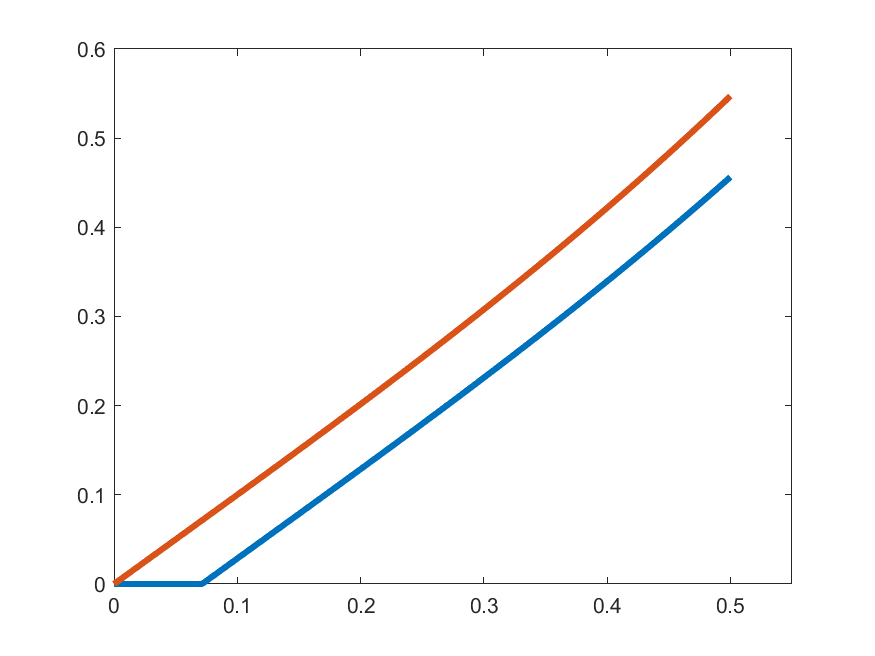
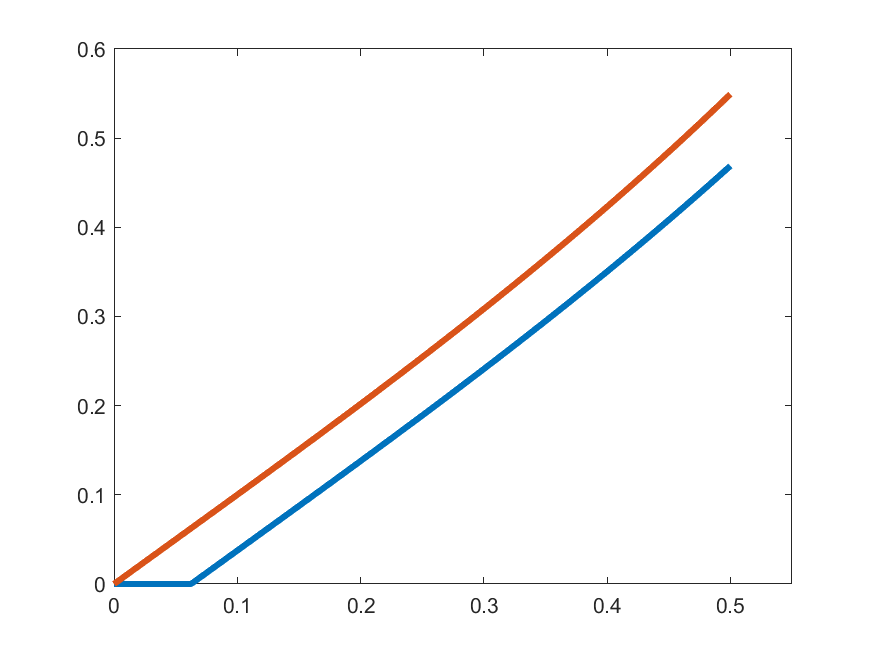
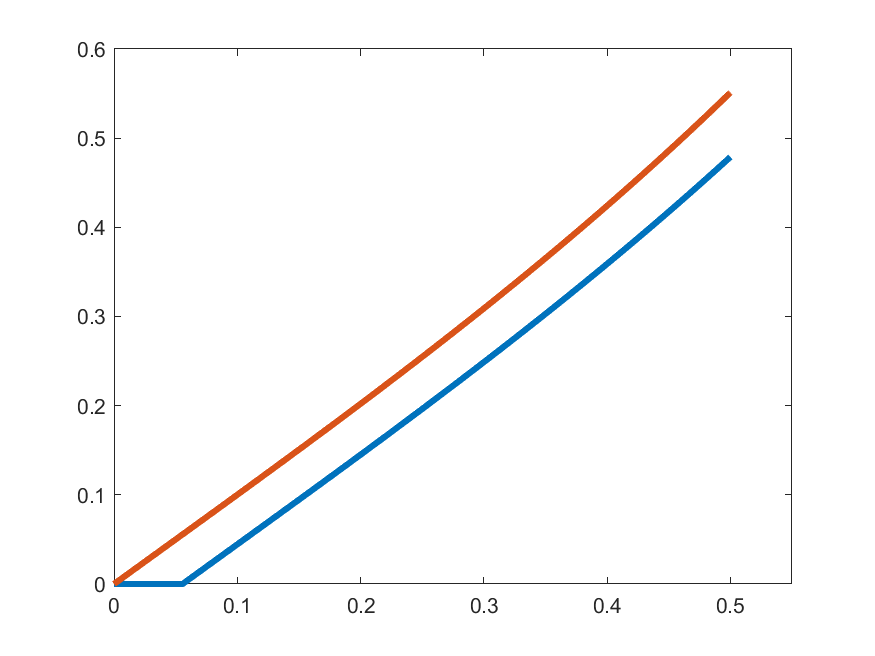
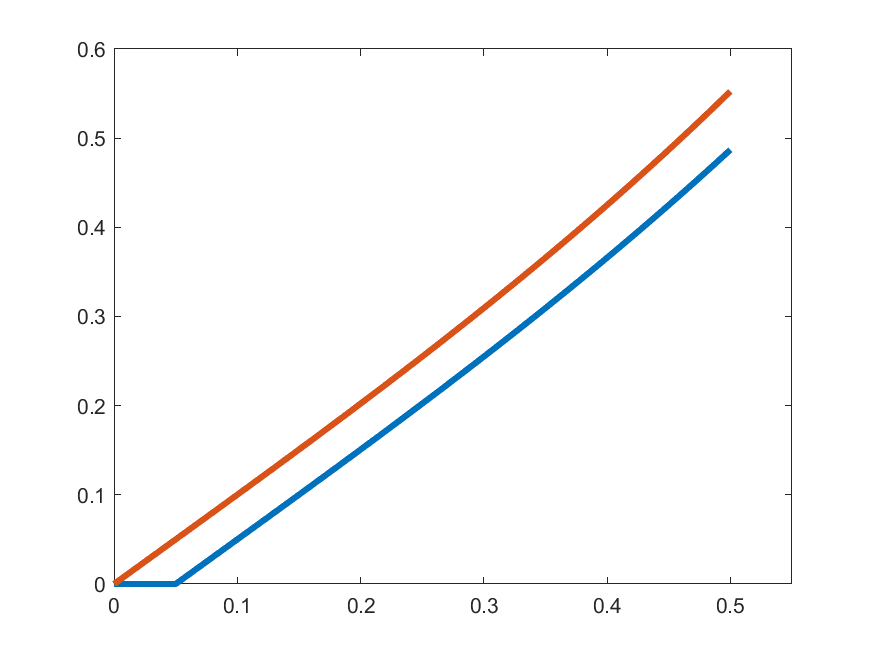
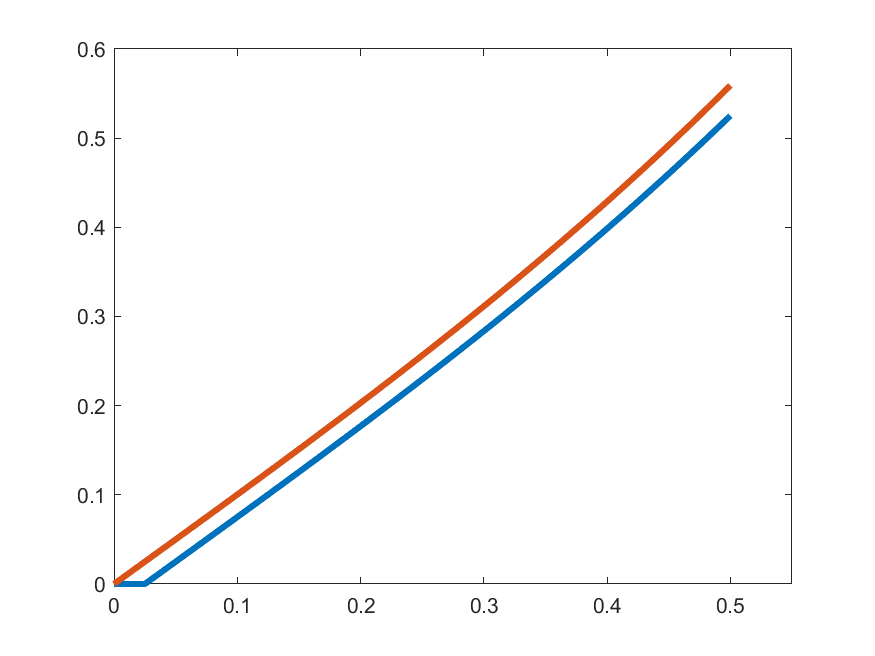
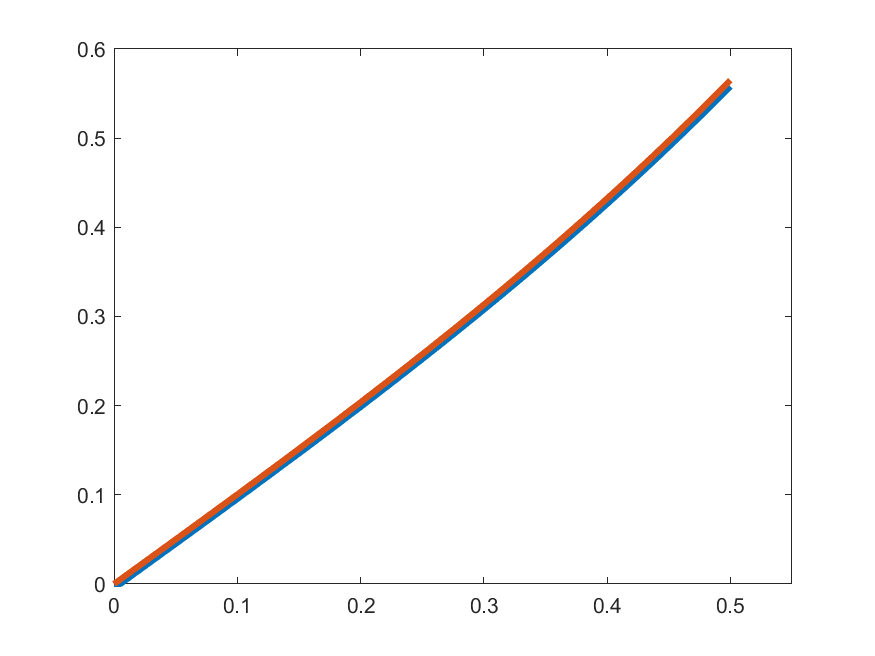
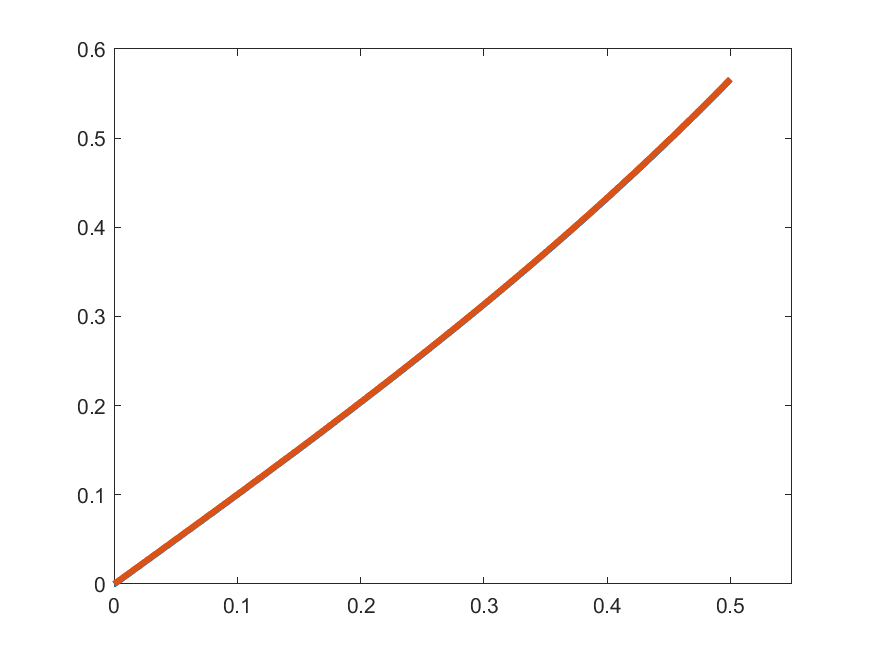
\(\gamma_{k}'(t)\)
\(t\gamma_{k}(t)\)
\(k=2\)
\(k=3\)
\(k=4\)
\(k=5\)
Recall, we're trying to solve:
\[y'(t) = ty(t)\]
\(k=6\)
\(k=7\)
\(k=8\)
\(k=9\)
\(k=10\)
\(k=20\)
\(k=100\)
\(k=1000\)
So, let's see how close are \(\gamma_{k}'(t)\) and \(t\gamma_{k}(t)\):