New strongly regular graphs from real line packings

John Jasper

Air Force Institute of Technology

International Conference on Approximation Theory and Beyond

The views expressed in this talk are those of the speaker and do not reflect the official policy
or position of the United States Air Force, Department of Defense, or the U.S. Government.

https://slides.com/johnjasper/icatb23/

special optimizers have nice repn's

nice repn's \(\Rightarrow\) rare graphs

Outline

find vectors maximally "spread out"

Background

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

Measuring how "spread out" vectors are

\[\mu(\Phi) = \cos(\theta)\]

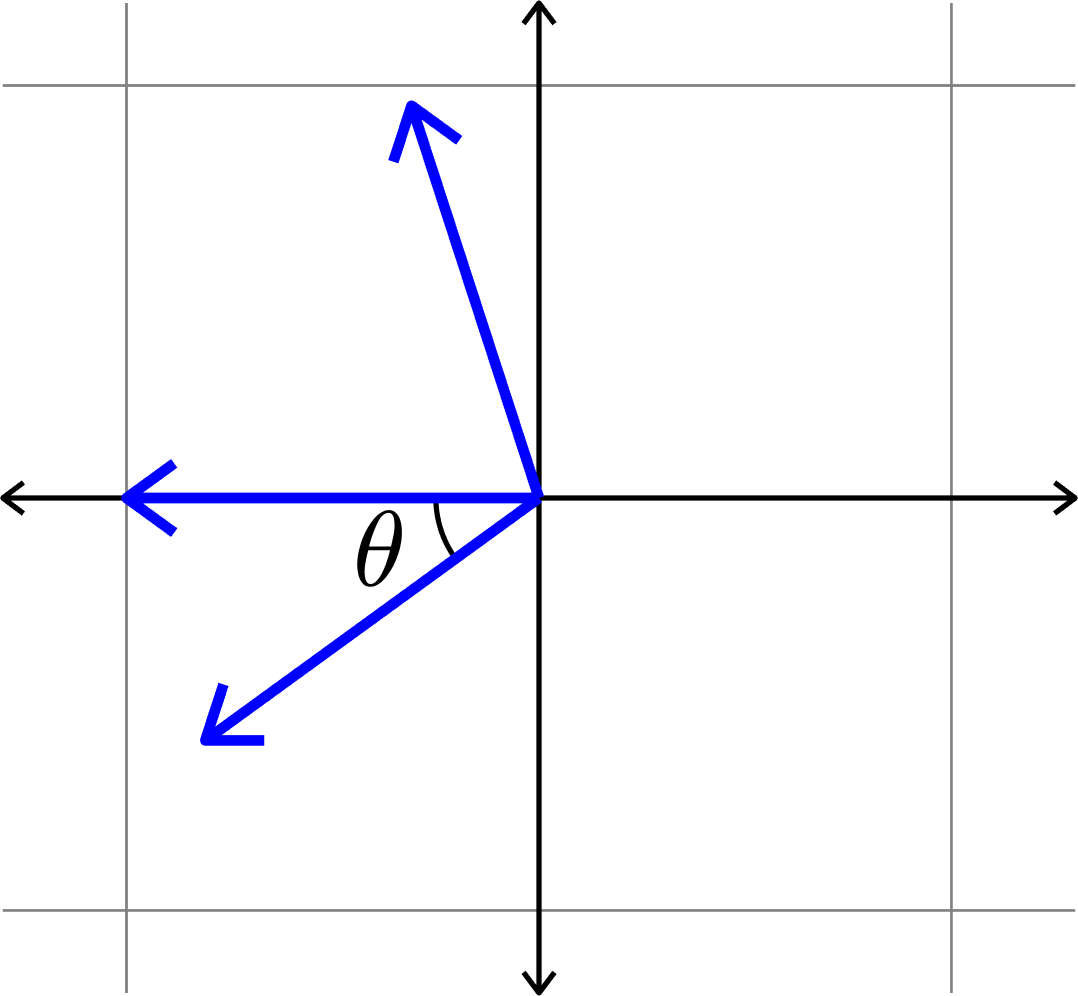
\(\mu(\Phi) = \cos(\theta)\)??

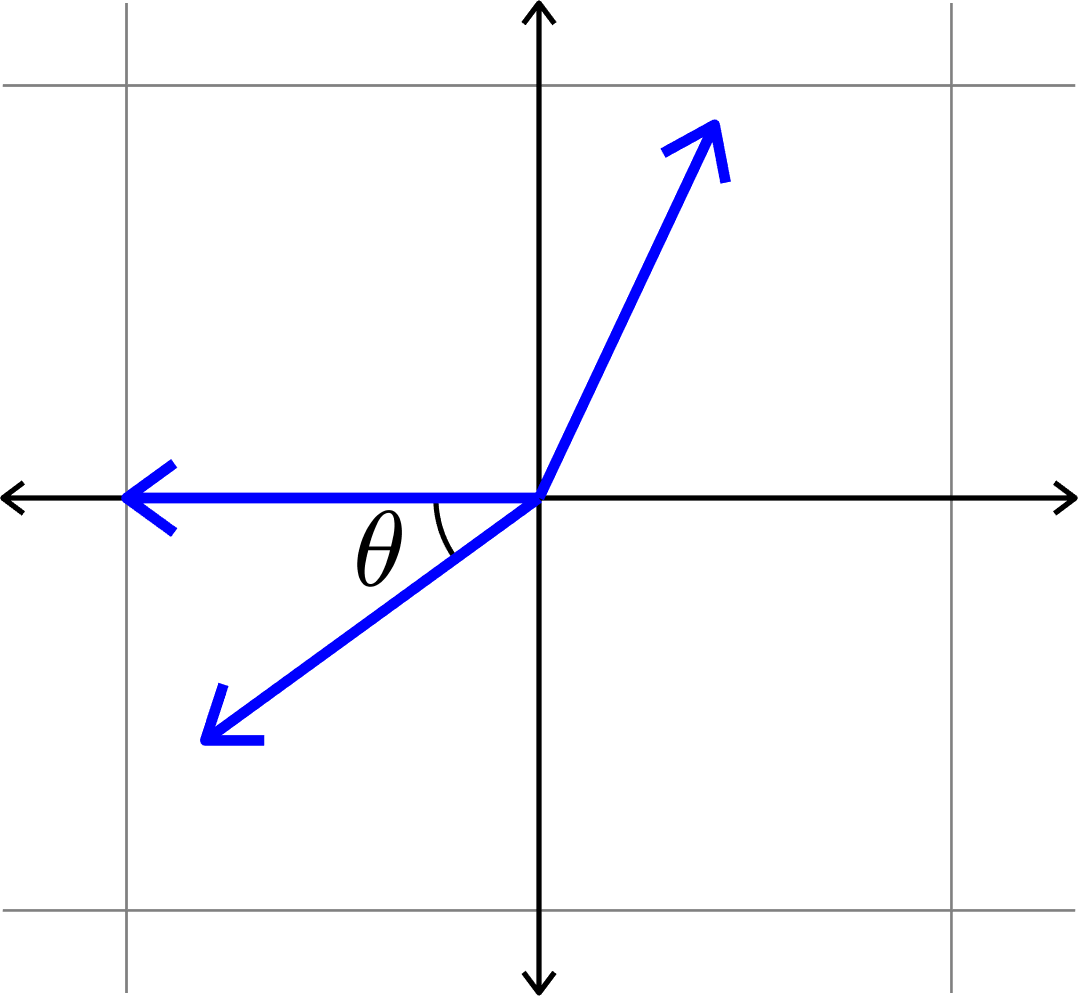
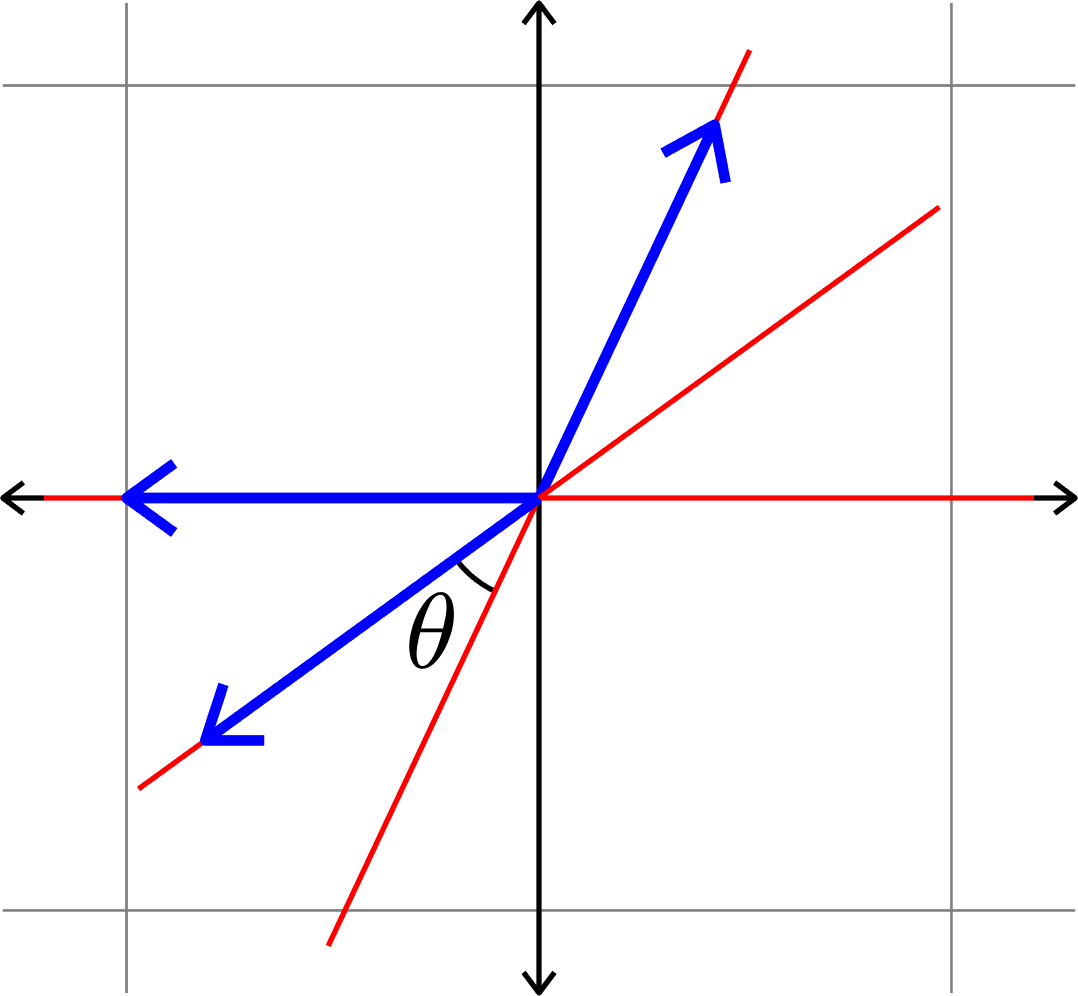
\(\mu(\Phi) = \cos(\theta)\)

Measuring how "spread out" vectors are

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

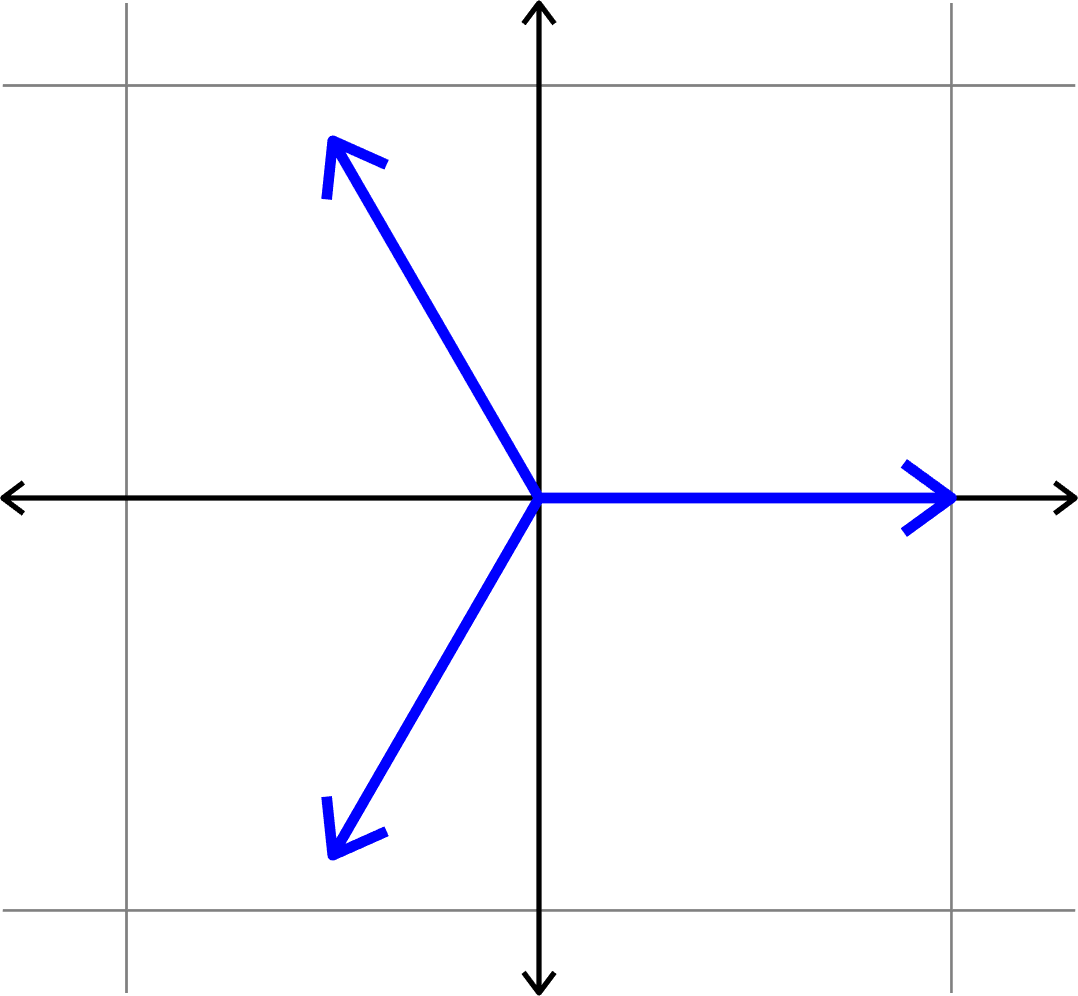
Example.

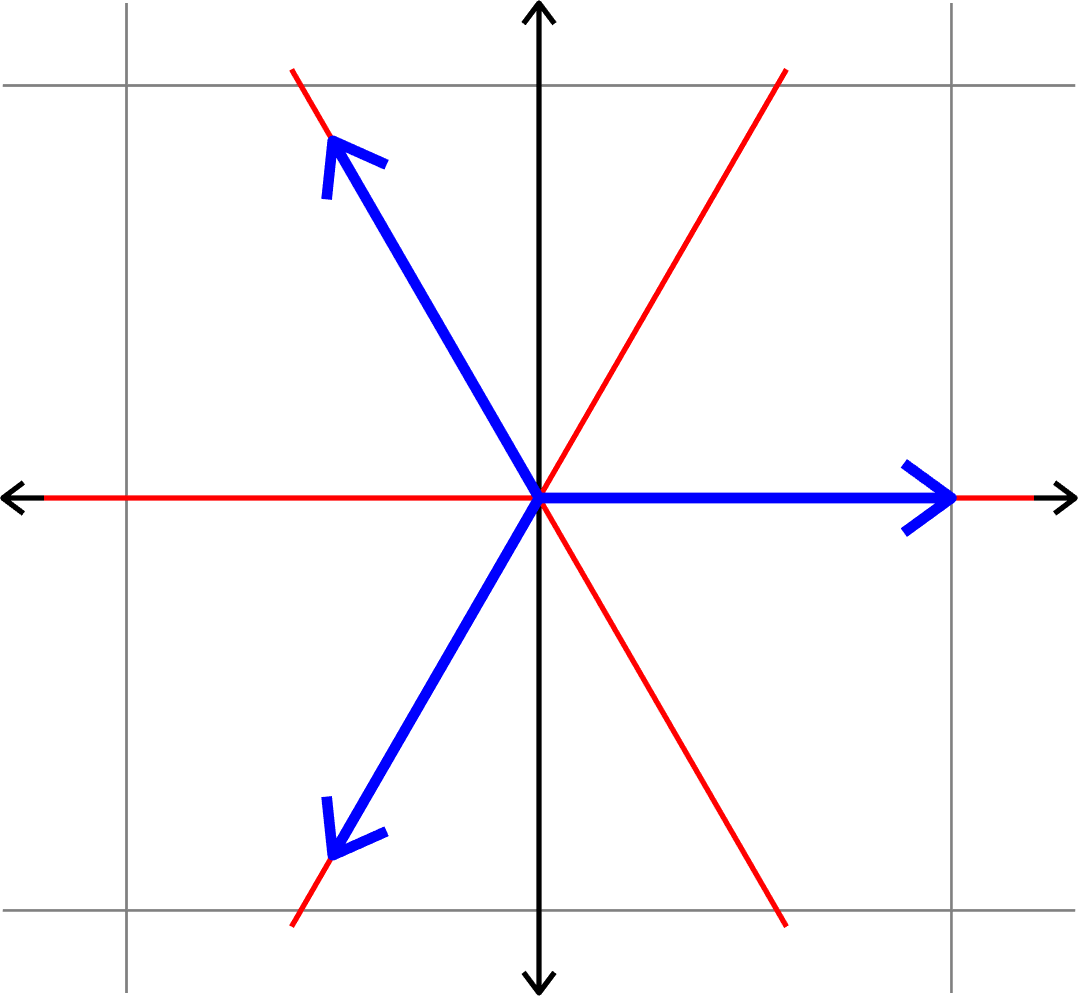
Measuring how "spread out" vectors are

Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence

\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]

Given \((d,N)\) find \(\Phi = (\varphi_{i})_{i=1}^{N}\subset\mathbb{R}^{d}\) such that \(\mu(\Phi)\) is minimal.

Vectors that are as spread out as possible

Theorem (the Welch bound). For unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{R}^d\)

\[\mu(\Phi)\geq \sqrt{\frac{N-d}{d(N-1)}}.\]

Equality holds if and only if both:

Tight: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]
Equiangular: There is a constant \(\alpha\) such that \[|\langle\varphi_{i},\varphi_{j}\rangle| = \alpha\quad\text{for all }i\neq j.\]

Welch bound equality \(\Longleftrightarrow\) equiangular tight frame (ETF)

ETF Gram matrix

Definition. Let \[\Phi = \big[\varphi_{1}\ \ \varphi_{2}\ \ \cdots\ \ \varphi_{N}\big]\in \mathbb{R}^{d\times N},\]

be a rank \(d\) matrix where each column \(\varphi_{n}\) is unit norm

\[\|\varphi_{n} \|^{2}=1.\]

1) (Tightness) \(\exists\,A>0\) such that \((\Phi^{\top}\Phi)^{2} = A\Phi^{\top}\Phi\).

2) (Equiangular) \(\exists\,B>0\) such that \(|\frac{1}{B}\varphi_{m}^{\top}\varphi_{n}^{}|=1\) for \(m\neq n\).

If both 1) and 2) hold, then \(\{\varphi_{n}\}_{n=1}^{N}\) is an ETF(\(d,N)\).

\[\Phi^{\top}\Phi = \left[\begin{array}{cccc} 1 & \varphi_{1}^{\top}\varphi_{2} & \cdots & \varphi_{1}^{\top}\varphi_{N}\\[1ex] \varphi_{2}^{\top}\varphi_{1} & 1 & \cdots & \varphi_{2}^{\top}\varphi_{N}\\[1ex] \vdots & \vdots & \ddots & \vdots\\[1ex] \varphi_{N}^{\top}\varphi_{1} & \varphi_{N}^{\top}\varphi_{2} & \cdots & 1\end{array}\right]\]

\(1\)'s down the diagonal

1) \(\Phi^{\top}\Phi \propto\) projection

2) \(|\varphi_{m}^{\top}\varphi_{n}^{}|\) constant

\(=\)

Steiner system

\(r\) ones per column

\(r\times (r+1)\) ETF with unimodular entries

"Steiner" ETF

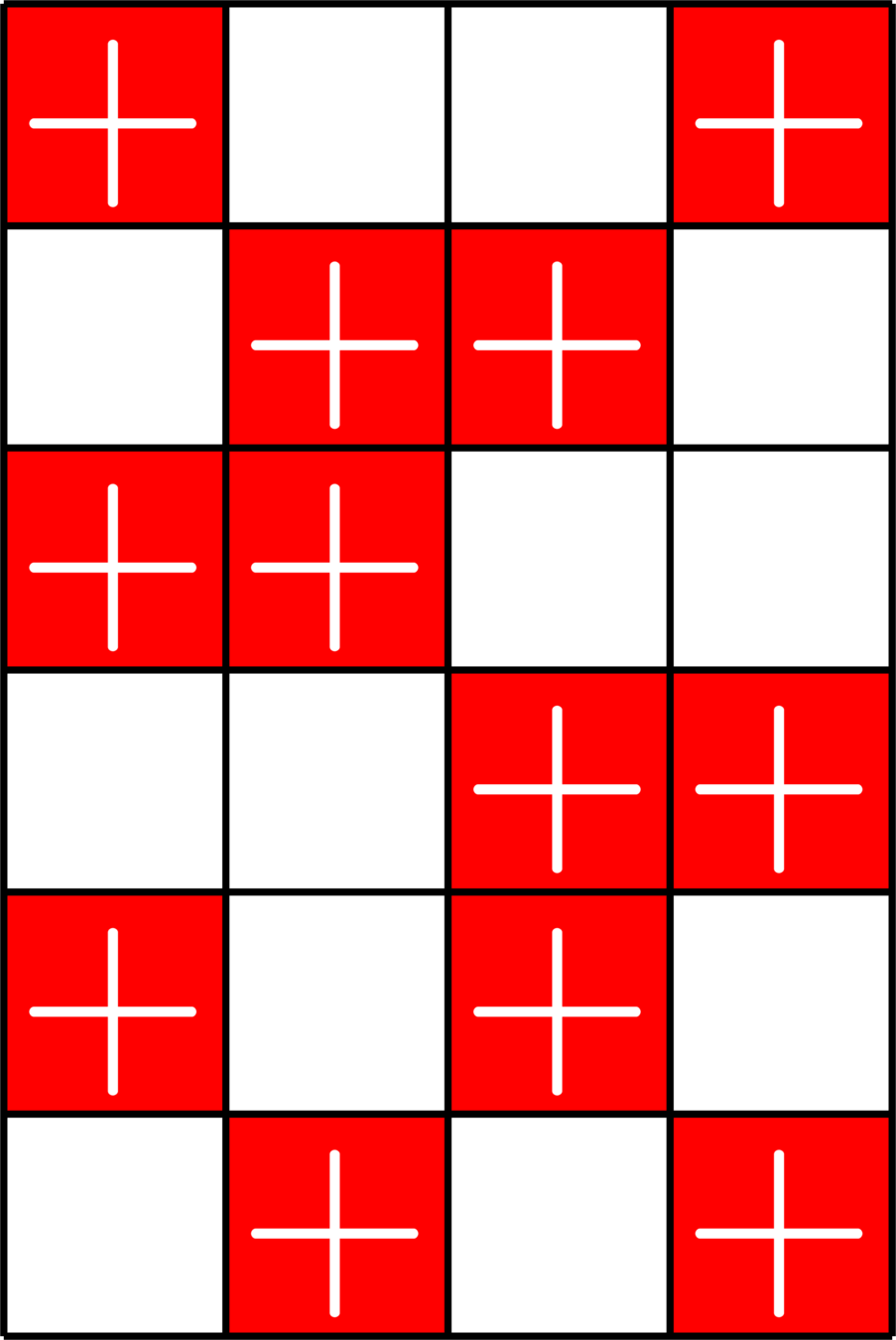
16 vectors in \(\mathbb{R}^{6}\)

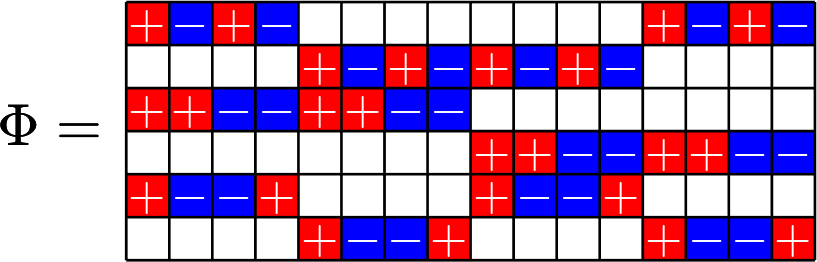
It's easy to go this way

\(\Phi^{\top}\Phi=\)

\(\Phi=\)

Gramians are forgetful

Given \(\Phi^{\top}\Phi\),

\(\Phi\) is only determined up to a unitary

\(\Phi^{\top}\Phi=\)

\(\Phi=\)

Gram matrix of ETF:

Adjacency matrix of graph:

ETFs \(\Rightarrow\) Graphs

Every vertex has 9 neighbors
Adjacent vertices have 4 common neighbors
Non-adjacent vertices have 6 common neighbors

Replace diagonal 1's with 0's

Replace -1's with 1's

Zero out the diagonal

Mult. by \(-1\)

Not regular!

Strongly Regular Graphs

Definition. An \(n\)-vertex graph is called strongly regular if

every vertex has \(k\) neighbors
adjacent vertices have \(\lambda\) common neighbors
nonadjacent vertices have \(\mu\) common neighbors

Such a graph is called an SRG\((n,k,\lambda,\mu)\).

Equivalently, the adjacency matrix \(G\) satisfies

\[G^{2} = k I + \lambda G + \mu(J-I-G)\quad\text{(where \(J\) is the all-ones matrix.)}\]

\(\Phi\) ETF \(\Rightarrow\) "quadratic relation":

\[(\Phi^{\top}\Phi)^{2} = A\,\Phi^{\top}\Phi.\]

But how many \(-1\)'s in each row ???

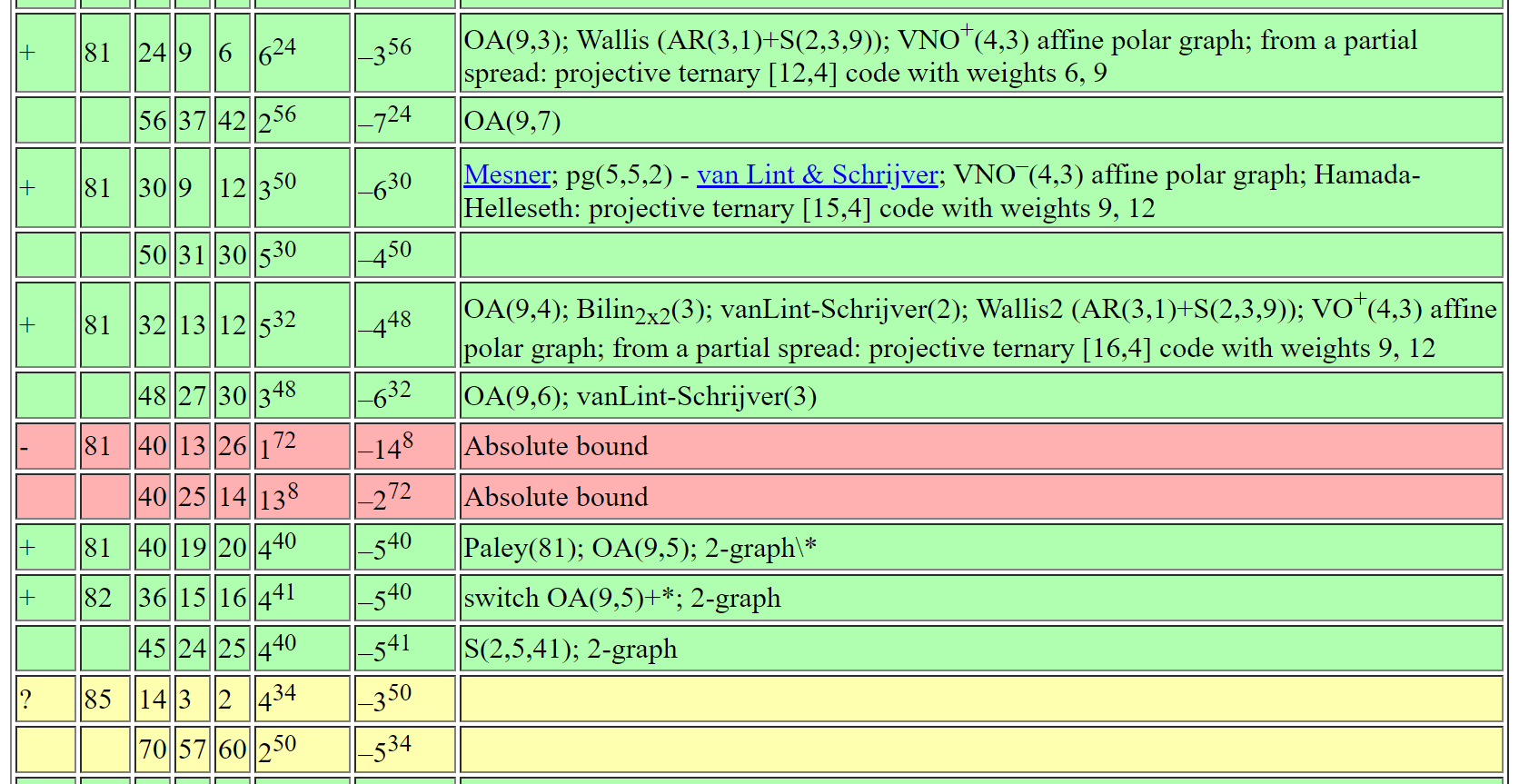
Andries Brouwer's Table of SRGs

= \(\nexists\)

= ???

= \(\exists\)

Goal: \(\mapsto\)

ETF \(\Rightarrow\) SRG

\(\Rightarrow\) the associated graph is regular and thus strongly regular

\(\mathbf{1}\) is an eigenvector of \(\Phi^{\top}\Phi\).

\(\mathbf{1} := (1,1,\ldots,1)\in\ker\Phi\)
\(\mathbf{1}\) \(\in\) row space of \(\Phi\), or

}

\(\Leftrightarrow\)

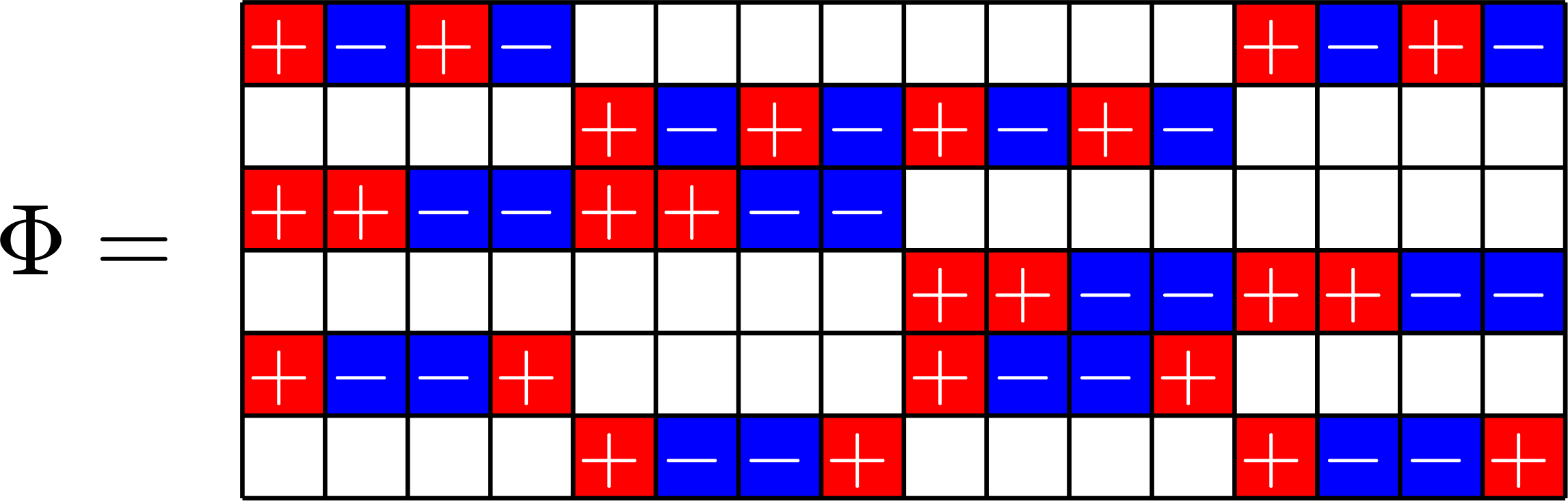
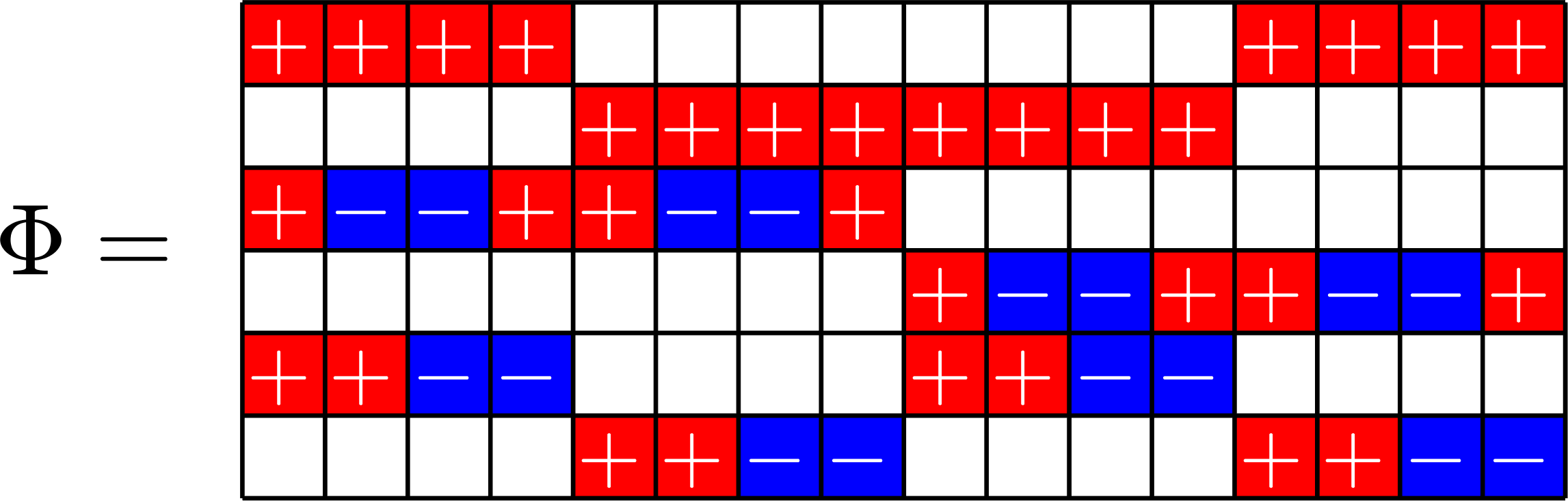
\(\mathbf{1}\) in row space

SRG\((16,5,0,2)\)

\(\mathbf{1}\in\ker\Phi\)

SRG\((16,9,4,6)\)

Example.

Nice ETF representation \(\Rightarrow\) new SRGs!

Suppose \(\Phi\) is an ETF:

Prototype

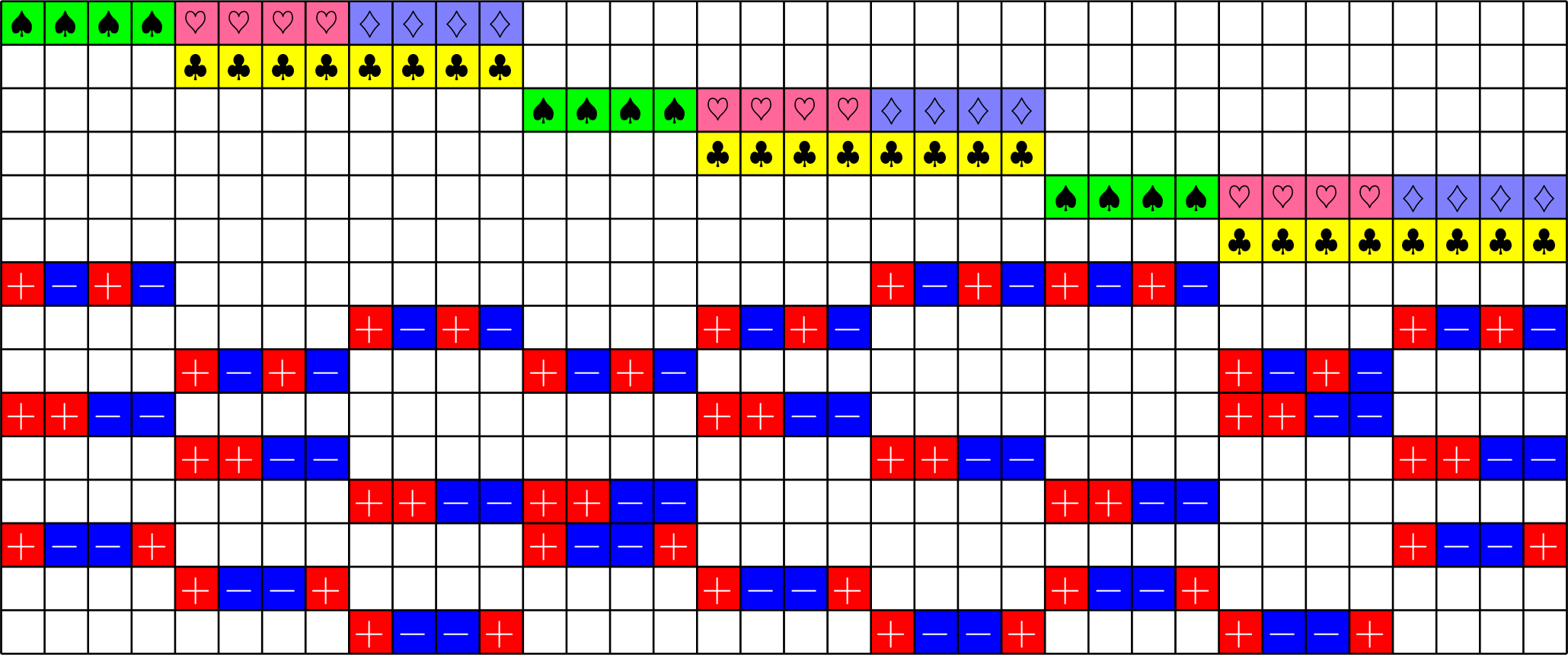
Tremain ETFs

\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]

\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\(\bigotimes\)

\(\sqrt{2}\)

\(\sqrt{\dfrac{1}{2}}\)

\(\sqrt{\dfrac{3}{2}}\)

Hadamard matrix

Steiner Triple System

Tremain ETFs

\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

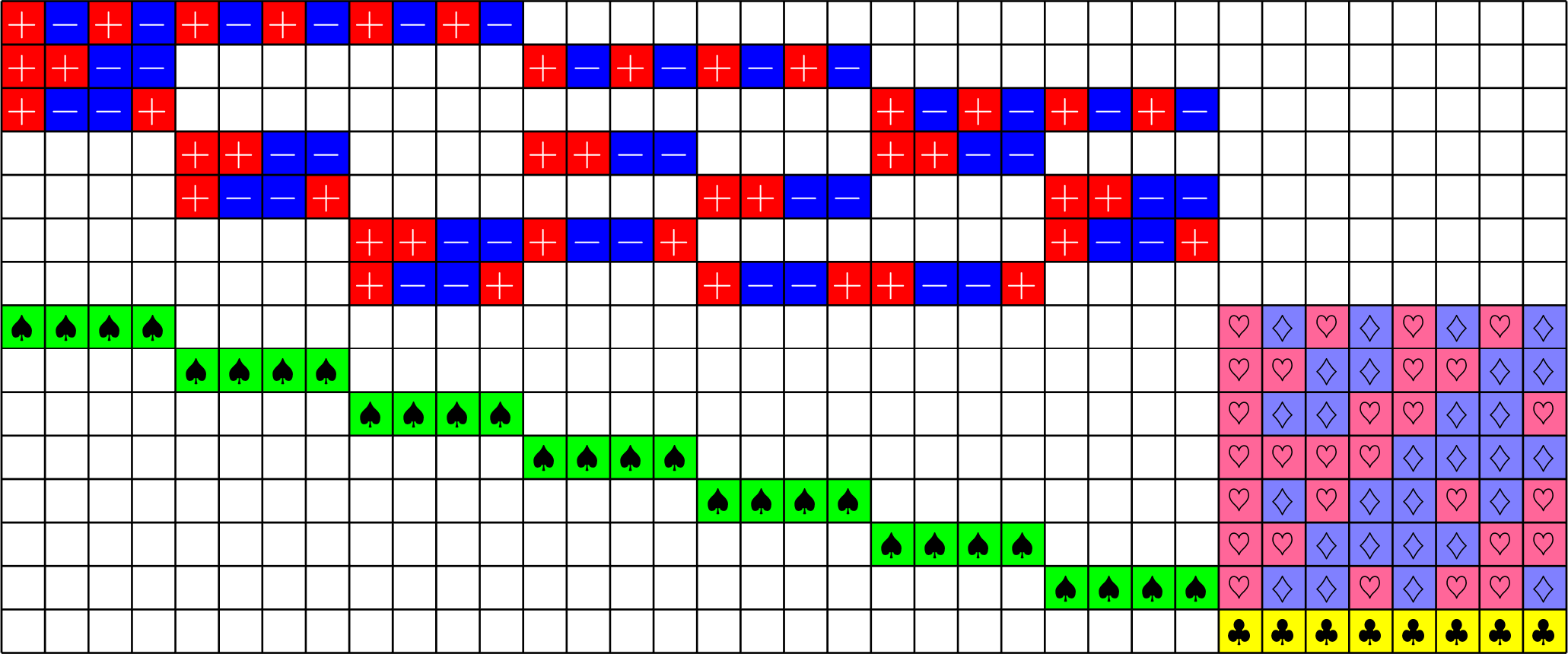
Tremain ETFs:

Theorem (Fickus, J, Mixon, Peterson '18). If there exists an

\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),

then there exists a \((2,3,2h-1)\)-Steiner system

and by the Tremain construction there exists a real \(d\times N\) ETF where \[d=\frac{1}{3}(h+1)(2h+1),\qquad N=h(2h+1).\]

\(51\times 136\) Tremain ETF

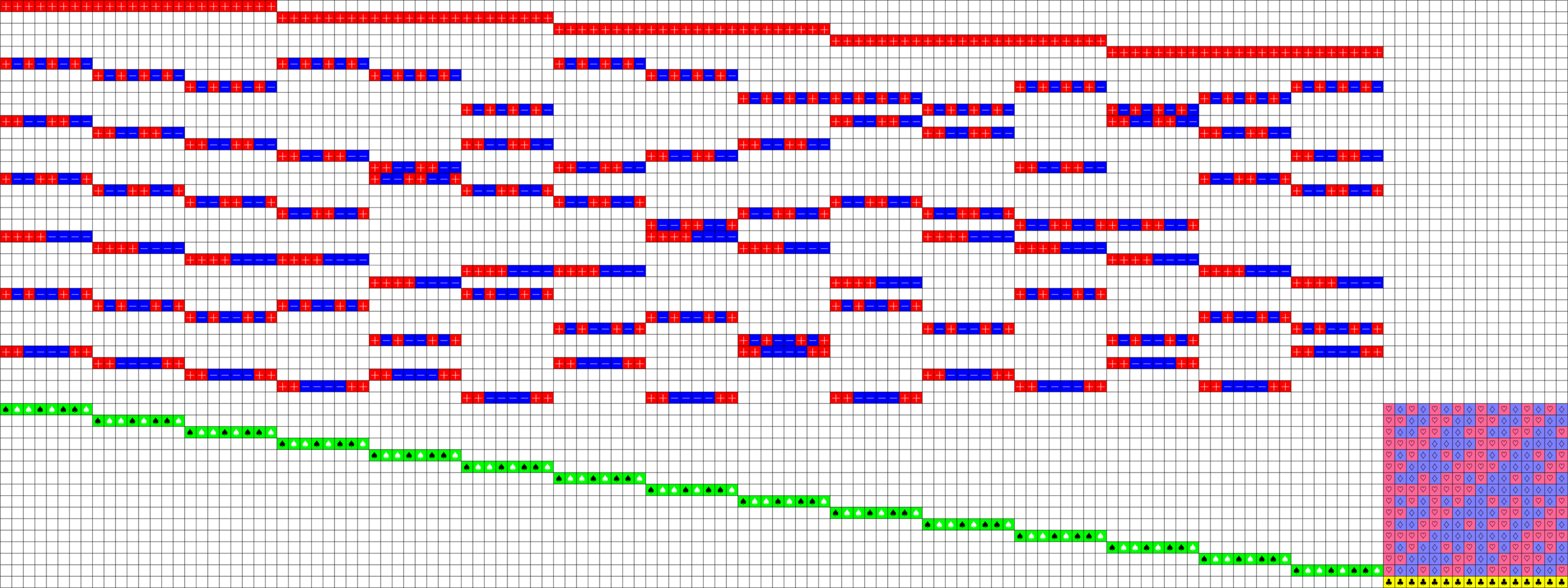
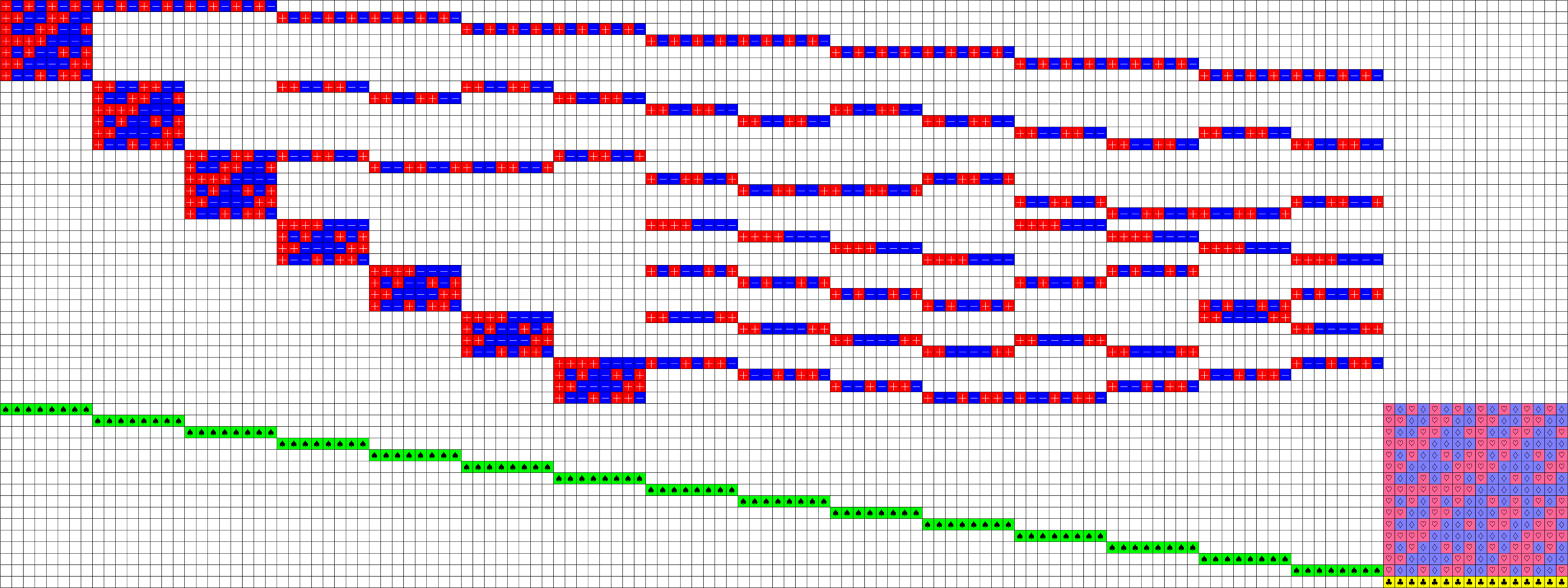
\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

\(\ =-\sqrt{2}\)

\(\ =-\sqrt{\dfrac{3}{2}}\)

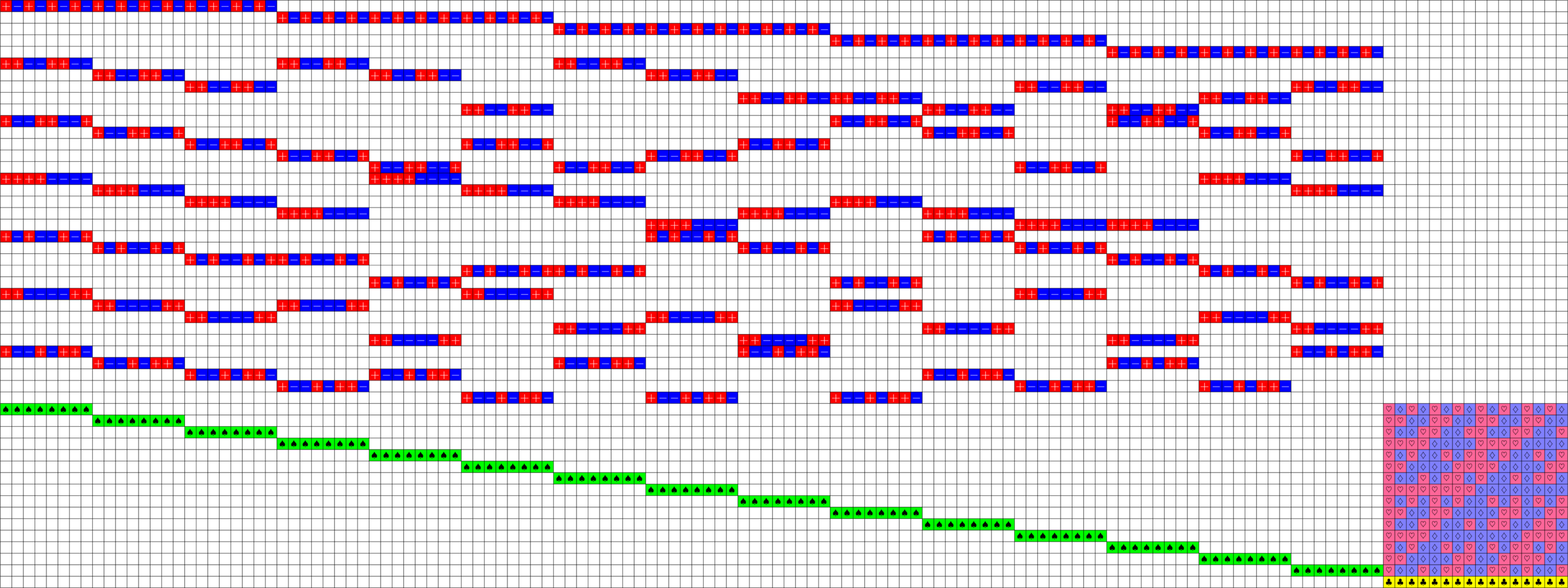
Axial Tremain ETFs:

Theorem (Fickus, J, Mixon, Peterson '18). If there exists an

\(h\times h\) Hadamard matrix with \(h\equiv 2\) \(\text{mod}\ 3\),

then there exists a strongly regular graph with parameters:

\[v=h(2h+1),\ k=\frac{(h+2)(2h-1)}{2},\ \lambda=\frac{(h-1)(h+4)}{2},\ \mu = \frac{h(h+2)}{2}\]

This gave us a new ETF!

From Brouwer's table online:

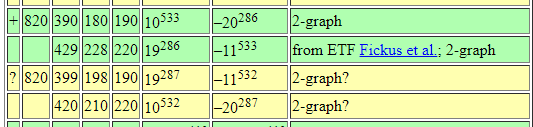
Let's replicate this success!

New Results

How can I make these vectors sum to zero?

\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

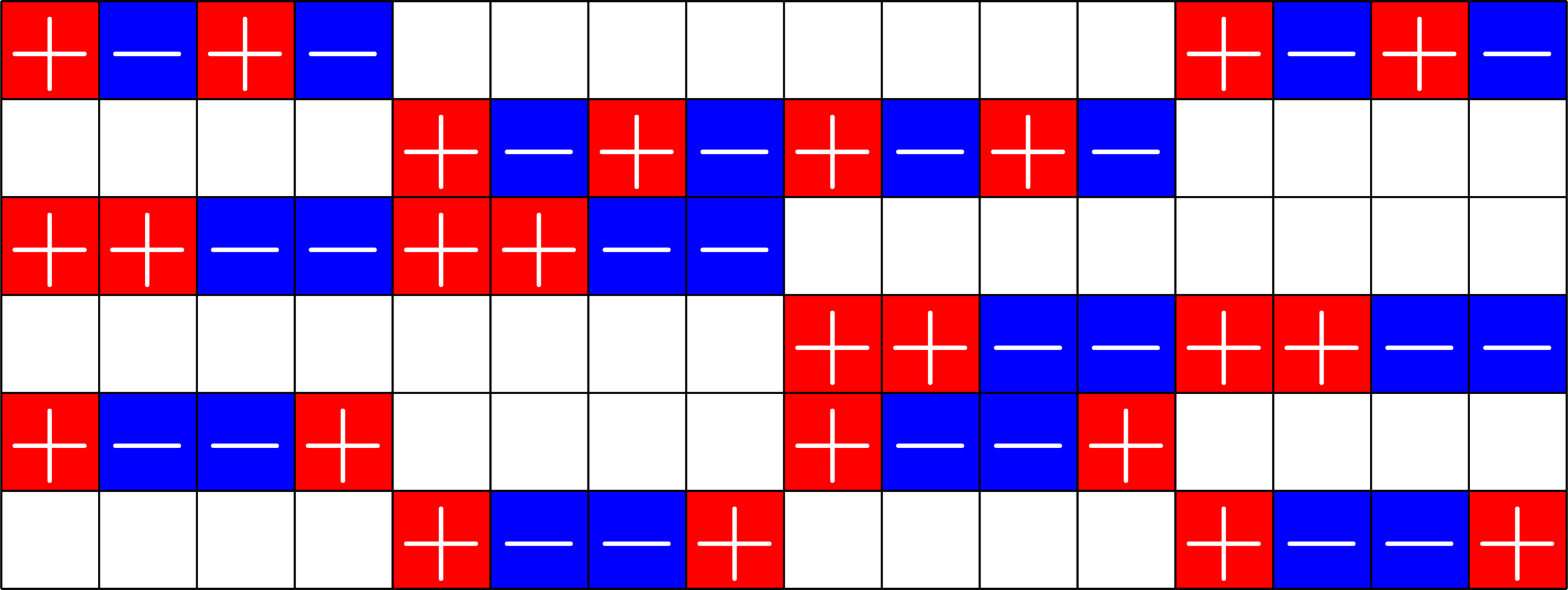
Graph from a \(15\times 36\) ETF with \(\boldsymbol{1}\) the kernel

Back to Brouwer's Table

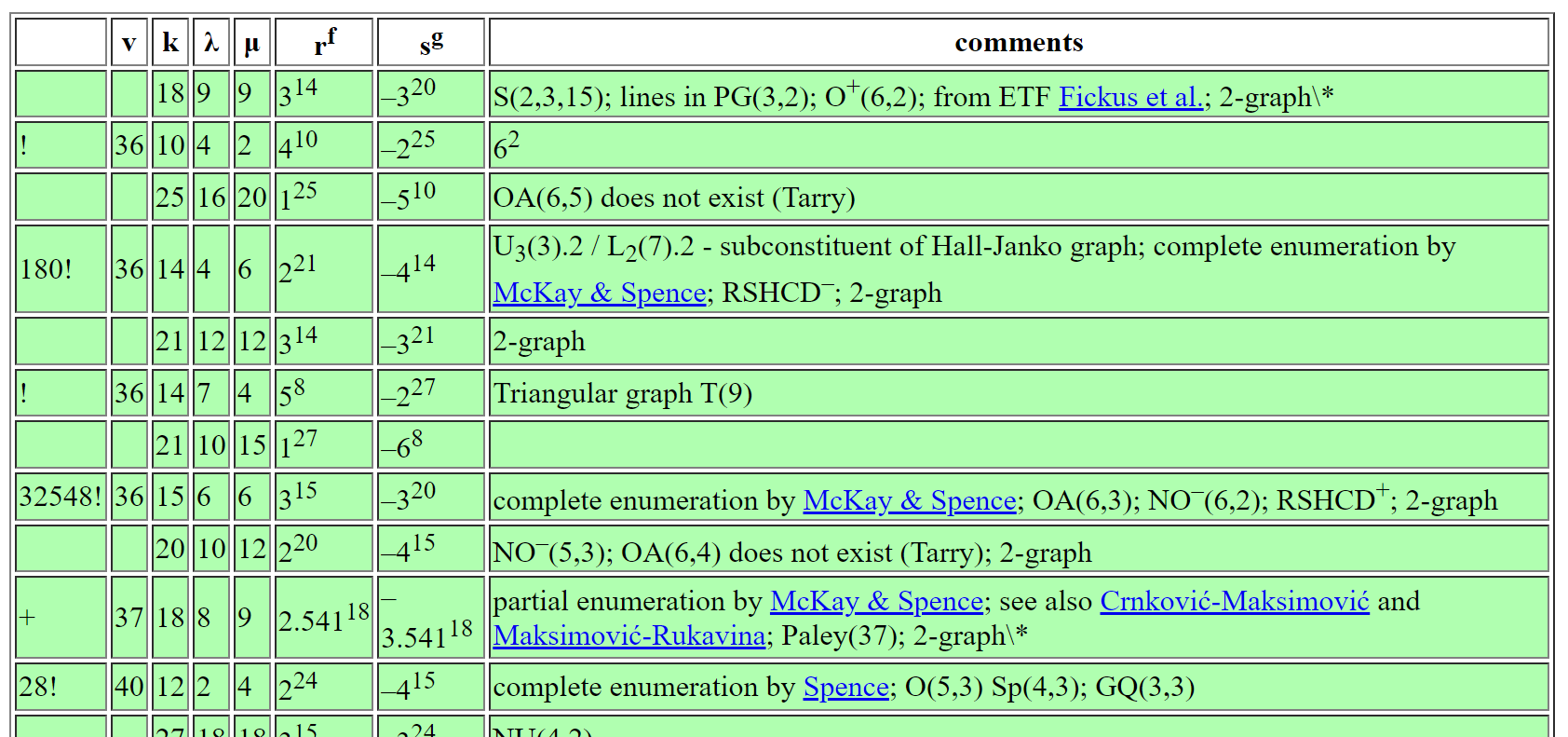
\(\operatorname{NO}^{-}\)(6,2)

Nice short fat repn ?

\(NO_{6}^{-}(2)\)

\(\Phi^{\top}\Phi=\)

\(\Phi=\)

Remember: Gramians are forgetful

\(NO_{6}^{-}(2)\)

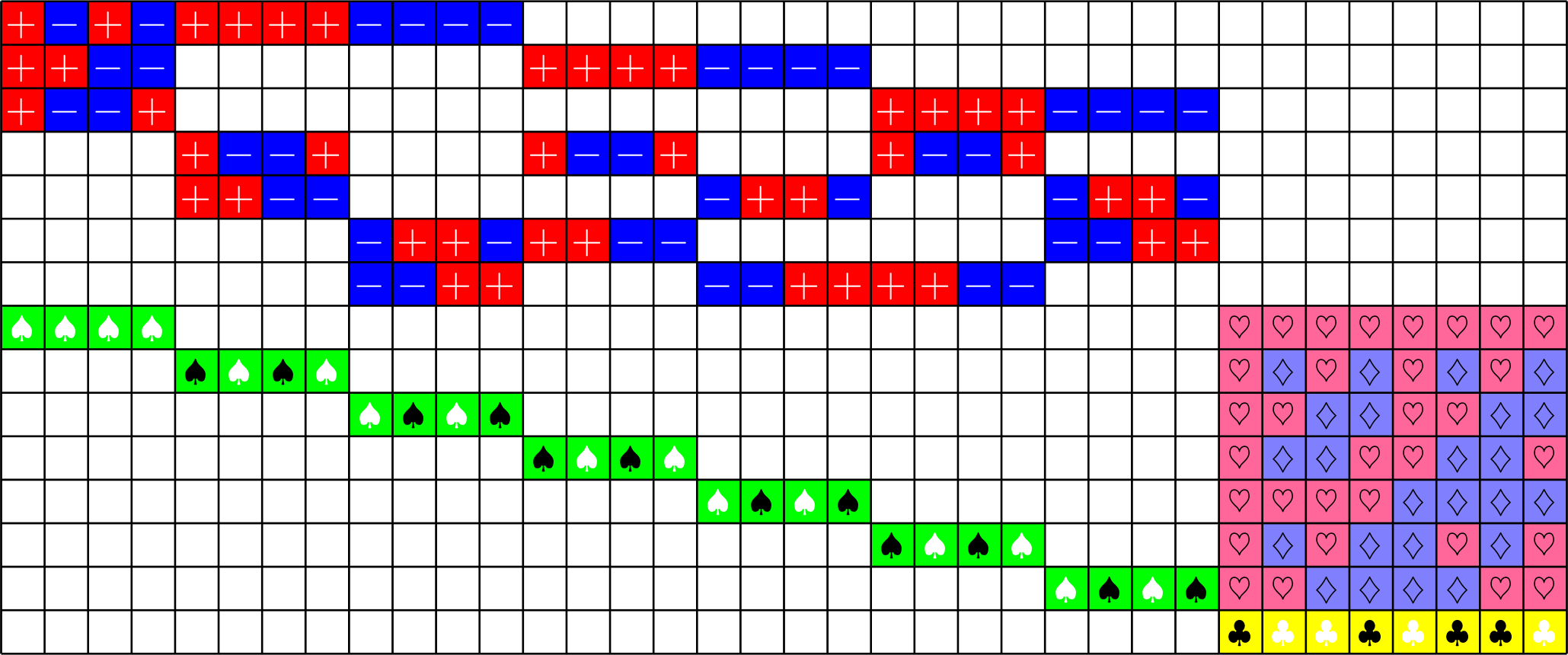
\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

\(\ =-\sqrt{2}\)

\(\ =-\sqrt{\dfrac{3}{2}}\)

\(NO_{6}^{-}(2)\)

\(\mathbf{1} = (1,1,\ldots,1)\) is in the kernel
works for all real Tremain ETFs!

Centered Tremain ETFs:

Theorem (J). If there exists an

\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),

then there exists a strongly regular graph with parameters

\[v=h(2h+1),\quad k=h^2-1,\quad \lambda=\frac{1}{2}(h^2-4),\quad \mu = \frac{1}{2}h(h-1)\]

\(\exists\, 20\times 20\) Hadamard matrix \(\Rightarrow\) SRG(820,399,198,190)

From Brouwer's table online:

\(\exists\, 20\times 20\) Hadamard matrix \(\Rightarrow\) SRG(820,399,198,190)

\(\bigotimes\)

\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]

\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\(I_{3}\otimes\)(\(2\times 3\) ETF)

Hadamard Matrix

Group Divisible Design (GDD)

Group Divisible Design

\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

\(\ =-\sqrt{2}\)

\(\ =-\sqrt{\dfrac{3}{2}}\)

Group Divisible Design

\(\ =+1\)

\(\ =-1\)

\(\ =\sqrt{2}\)

\(\ =-\sqrt{\dfrac{1}{2}}\)

\(\ =+\sqrt{\dfrac{1}{2}}\)

\(\ =\sqrt{\dfrac{3}{2}}\)

\(\ =-\sqrt{2}\)

\(\ =-\sqrt{\dfrac{3}{2}}\)

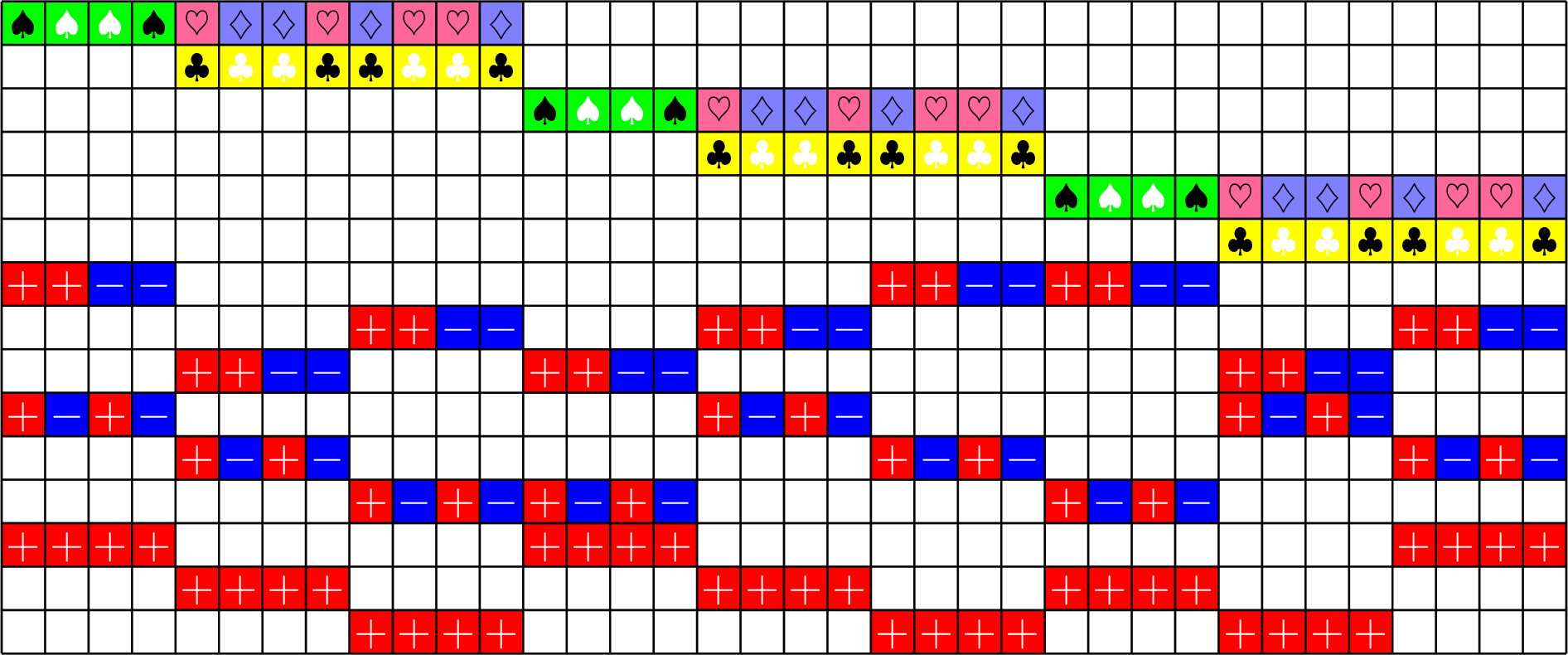
Axial GDD ETFs:

Theorem (J). If there exists an

\(h\times h\) Hadamard matrix with \(h\equiv 1\) \(\text{mod}\ 3\),

then there exists a strongly regular graph with parameters

\(\exists\,16\times 16\) Hadamard matrix \(\Rightarrow\exists\) SRG(528,279,150,144)

From Brouwer's table online:

\[v=h(2h+1),\ \ k=\frac{(h+2)(2h-1)}{2},\ \lambda=\frac{(h-1)(h+4)}{2},\ \mu = \frac{h(h+2)}{2}\]

\(\exists\,16\times 16\) Hadamard matrix \(\Rightarrow\exists\) SRG(528,279,150,144)

Tremain-sized ETFs

145

187

287

345

477

551

715

136

210

406

528

820

990

1378

1596

2080

\(d\)

\(N\)

Exists

Centered

Axial

Yes

Finding an axial \(77\times 210\)

Let \(\Phi\) be the known centered \(77\times210\).
We want to find \(x = \operatorname{argmin}_{\|x\|_{2} = 1}\|\Phi^{\top}x\|_{\infty}\)
Instead we find \(x = \operatorname{argmin}_{\|x\|_{2} = 1}\|\Phi^{\top}x\|_{4}\)
Gradient descent on many seeds
\(\Phi^{\top}x\) is \(\pm1\) vector \(\Rightarrow\) Profit!

There exists an SRG(210,95,40,45)

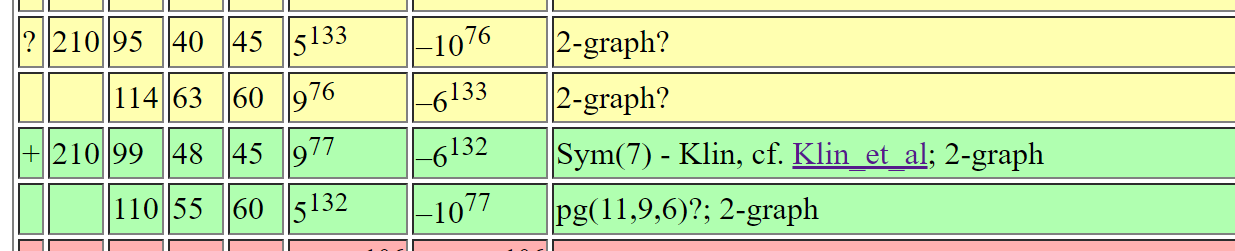
From Brouwer's table online:

There exists an SRG(210,95,40,45)

Thanks!

This work was partially supported by NSF #1830066
Webpage: https://tinyurl.com/jasperAFIT
Slides: https://slides.com/johnjasper