Day 1:
Vectors, Matrices, and the Column Space
What are we studying and why?
The main object of study in this course are simply lists of numbers, which we will write as columns of numbers, and we will refer to as vectors:
For example: \(\left[\begin{matrix}2\\0\\-3\end{matrix}\right]\), \(\left[\begin{matrix}2\\0.5\end{matrix}\right]\), \(\left[\begin{matrix} -0.71\\0.2\\3\\ 0.117\\ 3.001\end{matrix}\right]\)
Vectors come up in many applications, but let's look at one.
An image is just a list of numbers (say between 0 and 255):
\[\begin{bmatrix} 127\\ 153\\ 179\\ 202\\ 221\\ 237\\ 248\\ 253\\ 253\\ 248\\ 237\\ 221\\ 202\\ 179\\ 153\\ 127\\ 101\\ 75\\ 52\\ 33\\ 17\\ 6\\ 1\\ 1\\ 6\\ 17\\ 33\\ 52\\ 75\\ 101\\ 127\\ \end{bmatrix}\]
\[\begin{bmatrix} 707\\ 400\\ 0\\ -276\\ 0\\ -62\\ 0\\ -29\\ 0\\ -17\\ 0\\ -11\\ 0\\ -8\\ 0\\ -5\\ 0\\ -4\\ 0\\ -1\\ 0\\ -2\\ 0\\ -1\\ 0\\ -1\\ 0\\ -1\\ 0\\ 0\\ 0\\ \end{bmatrix}\]
Transform your vector in an invertible way.
Throw away the small entries in your vector
Apply the inverse transform
\[\begin{bmatrix} 707\\ 400\\ 0\\ -276\\ 0\\ -62\\ 0\\ -29\\ 0\\ -17\\ 0\\ -11\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix}\]
\[\begin{bmatrix} 131\\ 149\\ 177\\ 204\\ 223\\ 237\\ 246\\ 252\\ 254\\ 249\\ 237\\ 220\\ 201\\ 179\\ 155\\ 127\\ 99\\ 75\\ 53\\ 34\\ 17\\ 5\\ 0\\ 2\\ 8\\ 17\\ 31\\ 50\\ 77\\ 105\\ 123 \end{bmatrix}\]
Original Image
Data to store
Compressed image

Original image:

Keeping the largest 20% of the entries in the transformed image
Keeping the largest 10% of the entries in the transformed image

Keeping the largest 5% of the entries in the transformed image

Keeping the largest 1% of the entries in the transformed image

Some important sets of vectors:
\(\mathbb{R}^{2} = \left\{\left[\begin{matrix}a\\ b\end{matrix}\right] : a\in\mathbb{R} \text{ and } b\in\mathbb{R}\right\}\)
\(\mathbb{R}^{3} = \left\{\left[\begin{matrix}a\\ b\\c\end{matrix}\right] : a\in\mathbb{R} \text{ and } b\in\mathbb{R} \text{ and } c\in\mathbb{R}\right\}\)
\(\mathbb{R}^{n} = \left\{\left[\begin{matrix}a_{1}\\ a_{2}\\\vdots\\a_{n}\end{matrix}\right] : a_{1}\in\mathbb{R},\ a_{2}\in\mathbb{R},\ \ldots \text{ and } a_{n}\in\mathbb{R}\right\}\)
(Note that the textbook uses \(\mathbf{R}\) for the set of real numbers instead of \(\mathbb{R}\).)
We represent a vector as an arrow with a tail and a head.
A vector has two properties:
- Direction
- Length
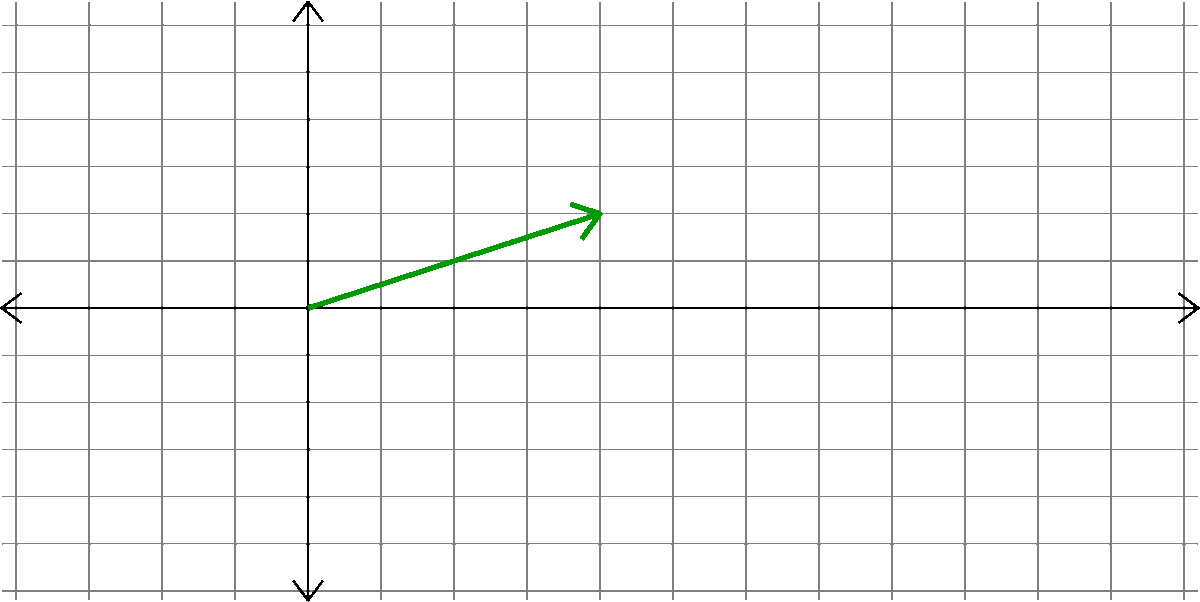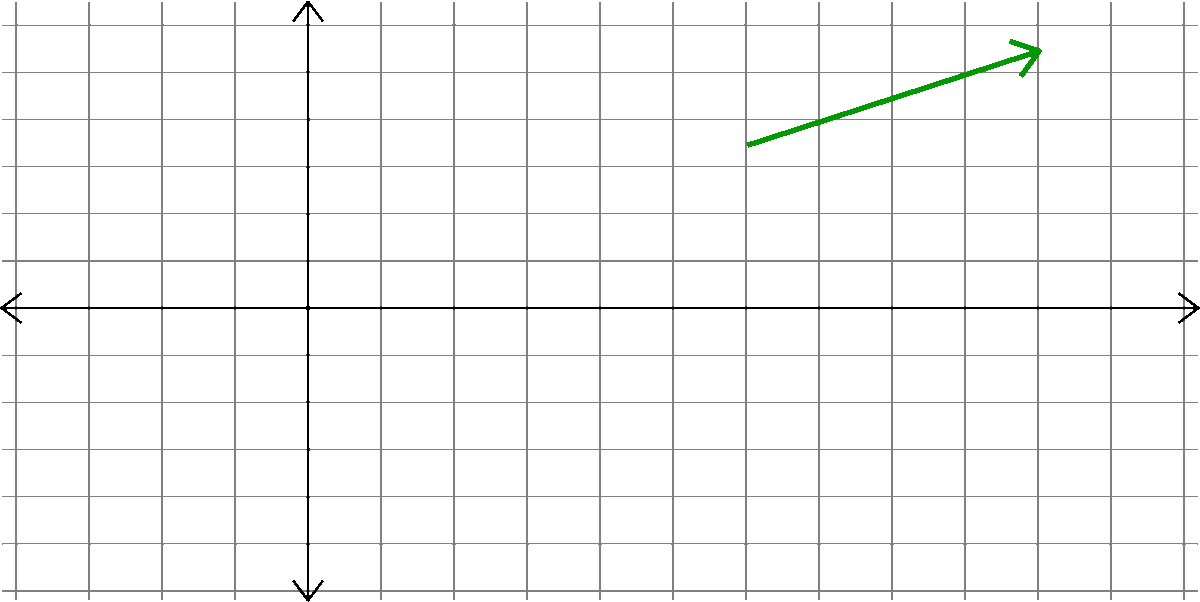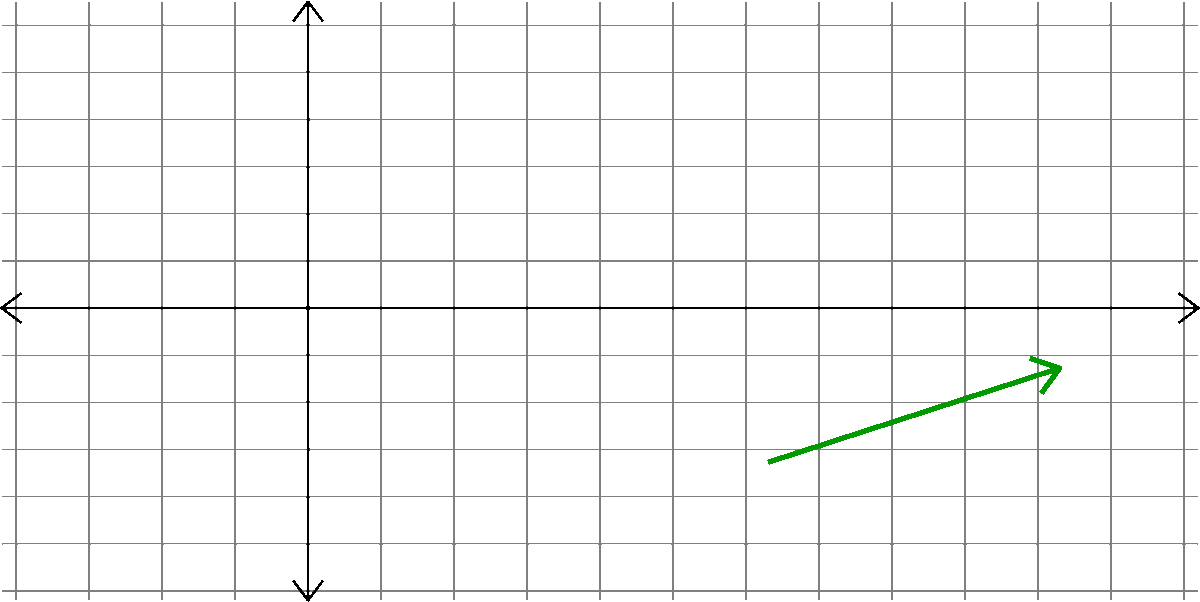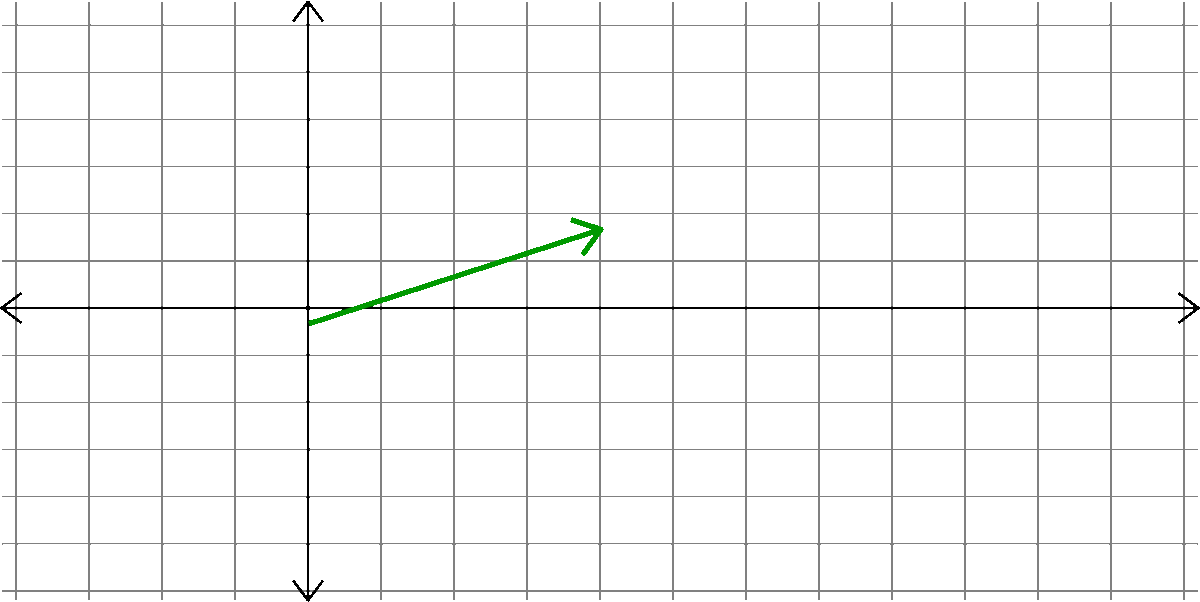
So, all of these are the same vector:
We represent a vector as an arrow with a tail and a head.
A vector has two properties:
- Direction
- Length
We label the vector by the head when the tail is at the origin.
\(\left[\begin{matrix}4\\ 2\end{matrix}\right]\)
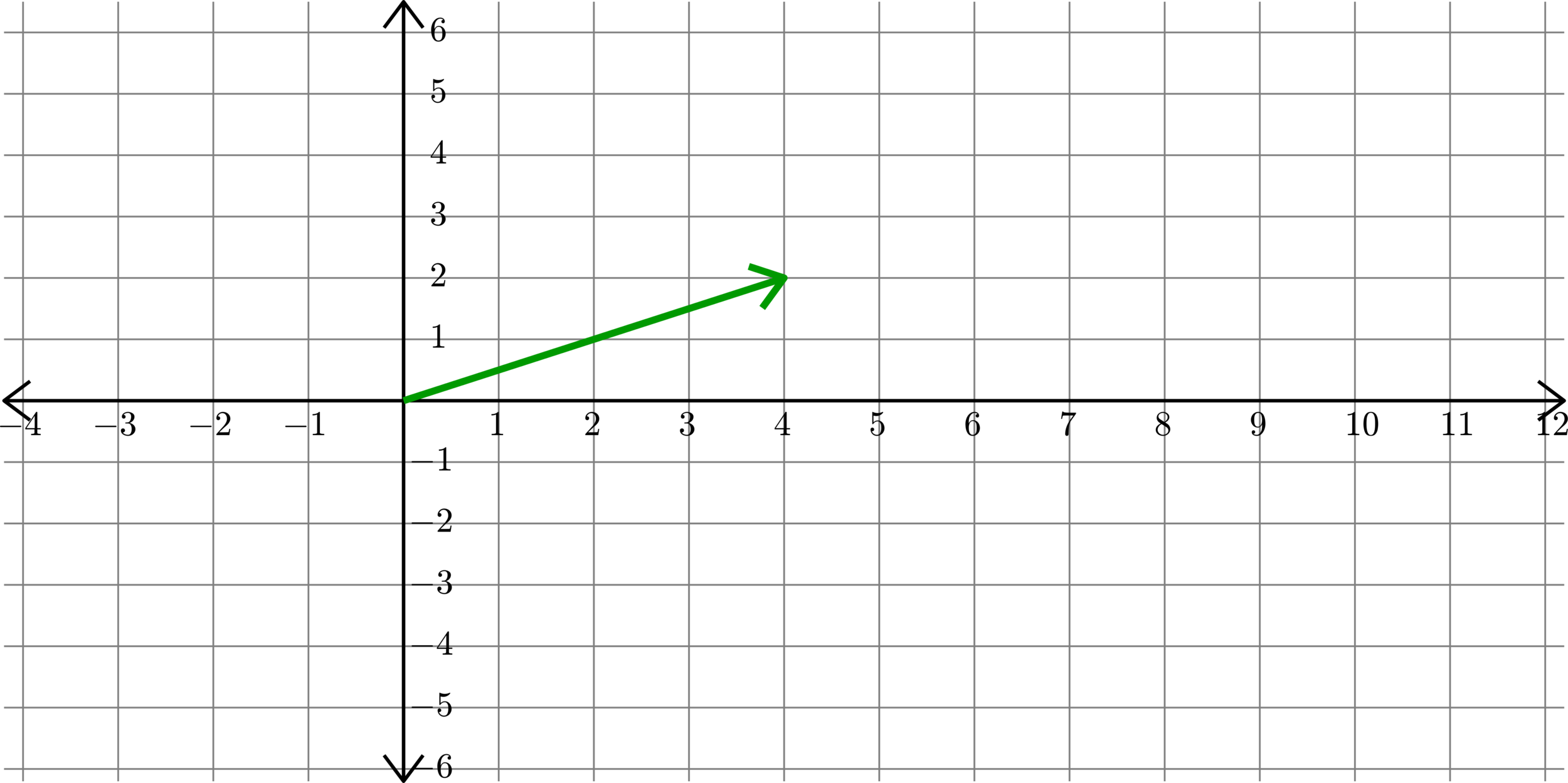
\(\left[\begin{matrix} a_{1}\\ a_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right]\)
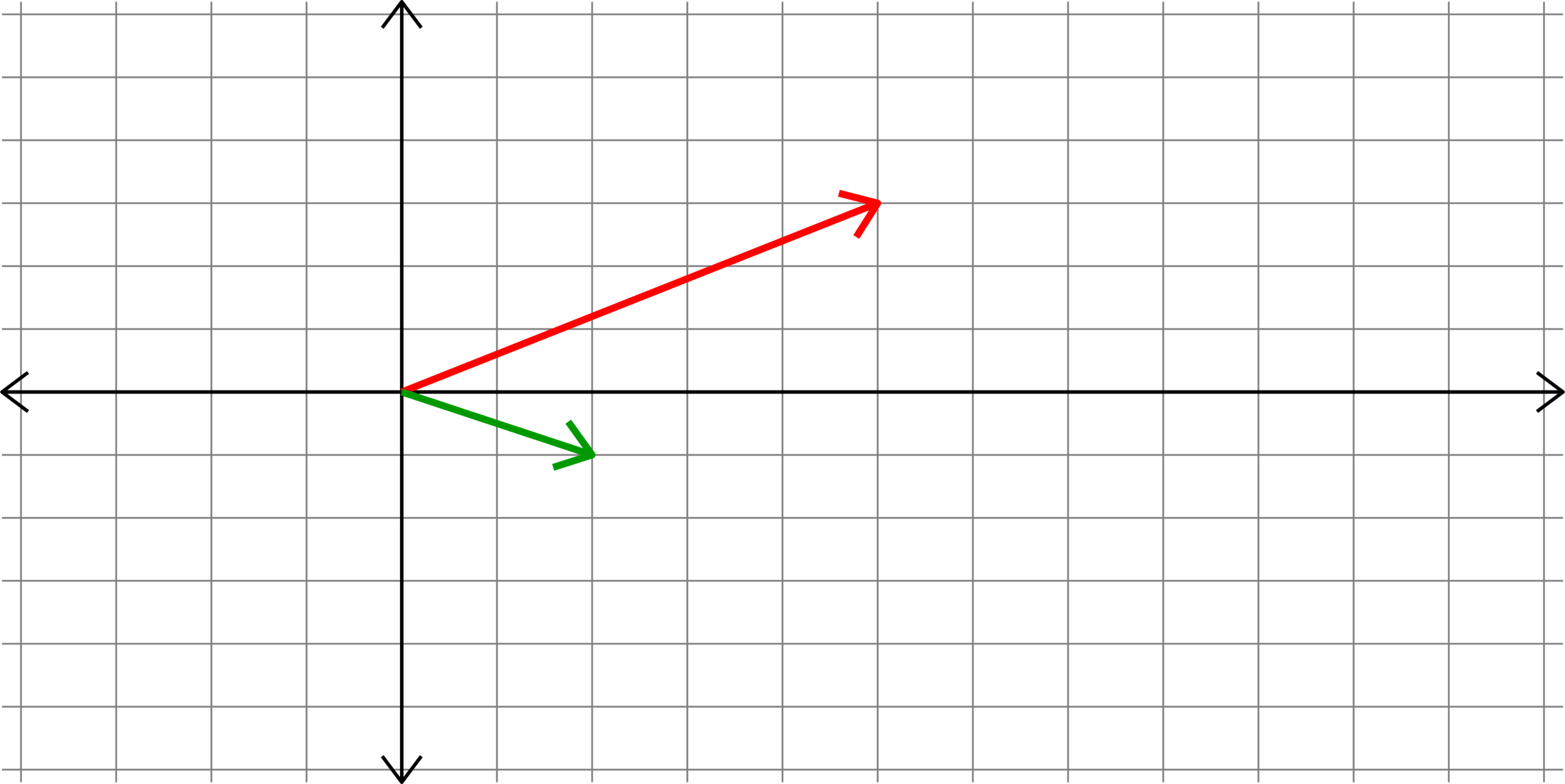
How do we add two vectors?
\(\left[\begin{matrix} a_{1}\\ a_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right]\)
How do we add two vectors?
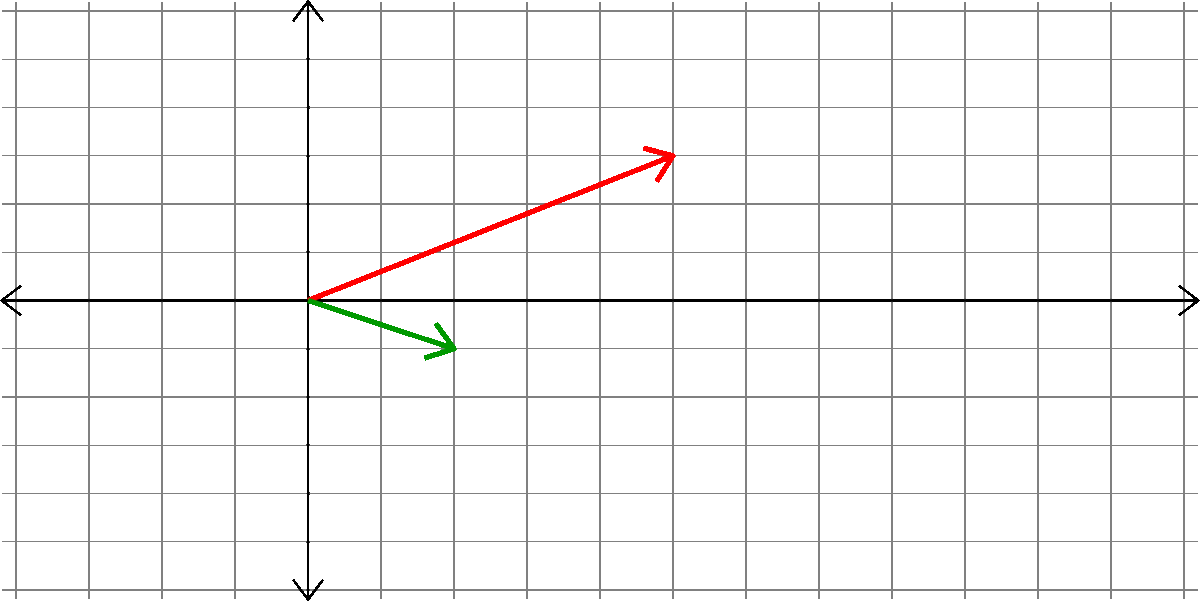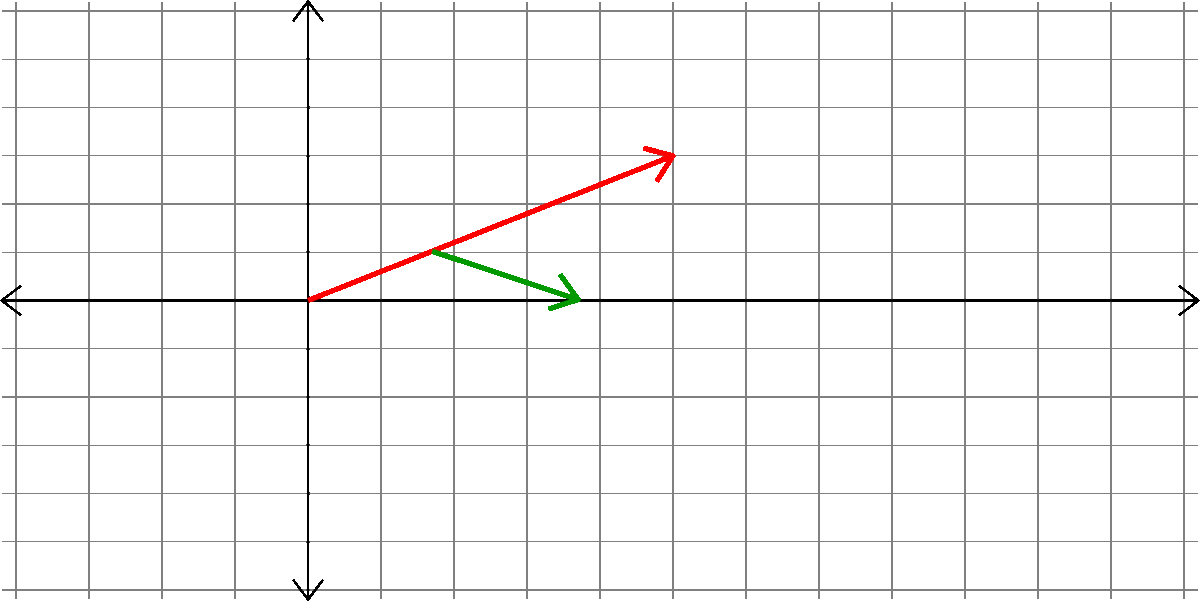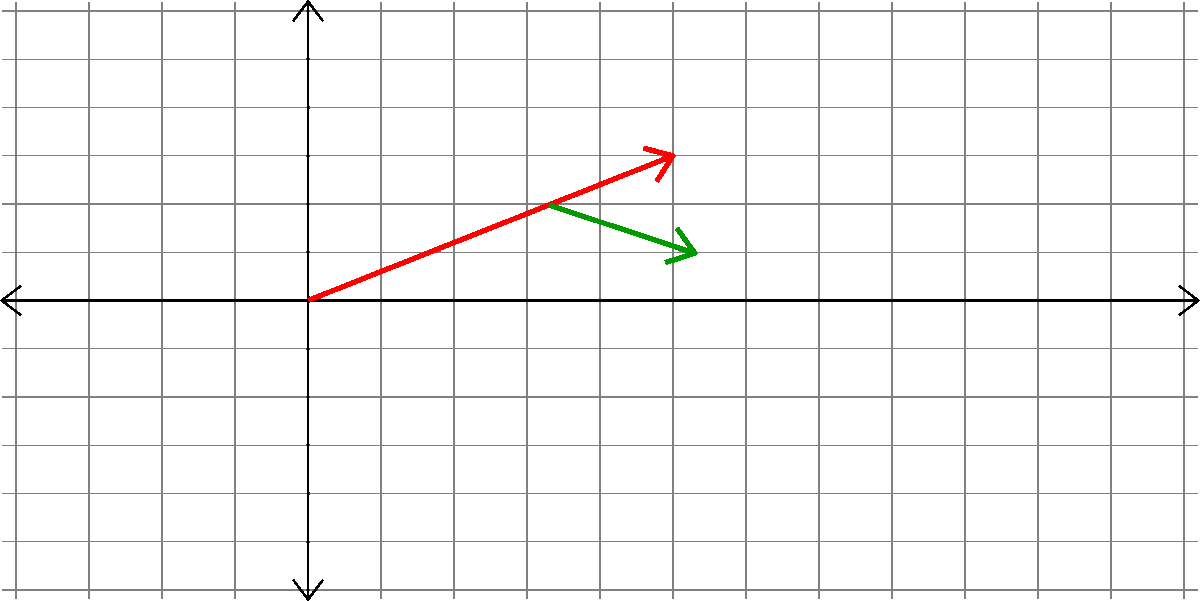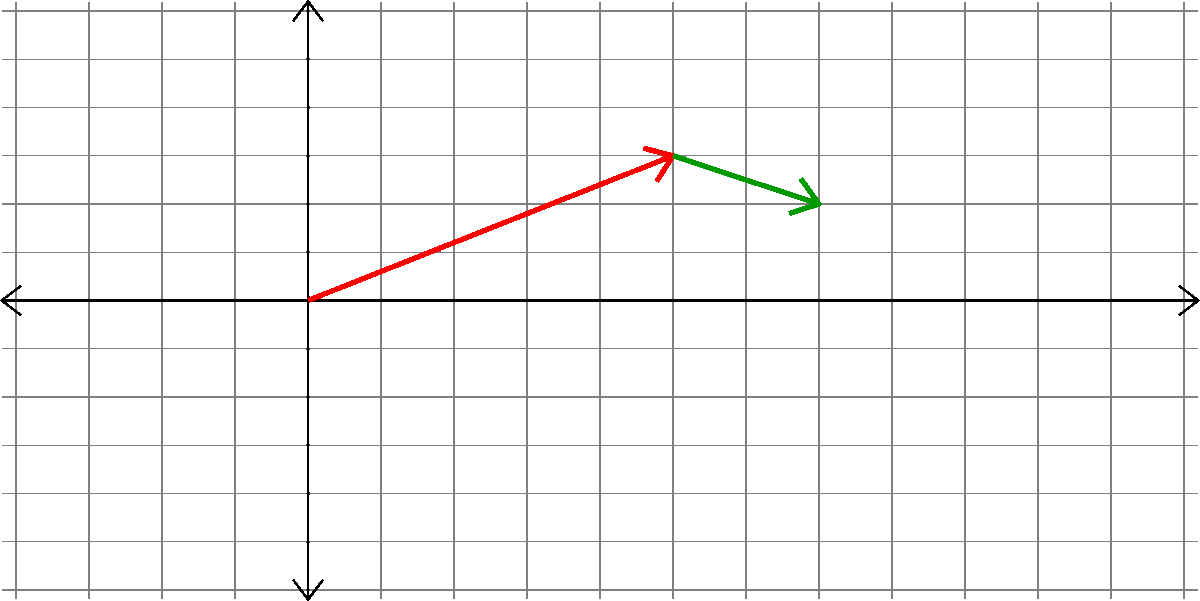
\(\left[\begin{matrix} a_{1}\\ a_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right]\)
+ =
??
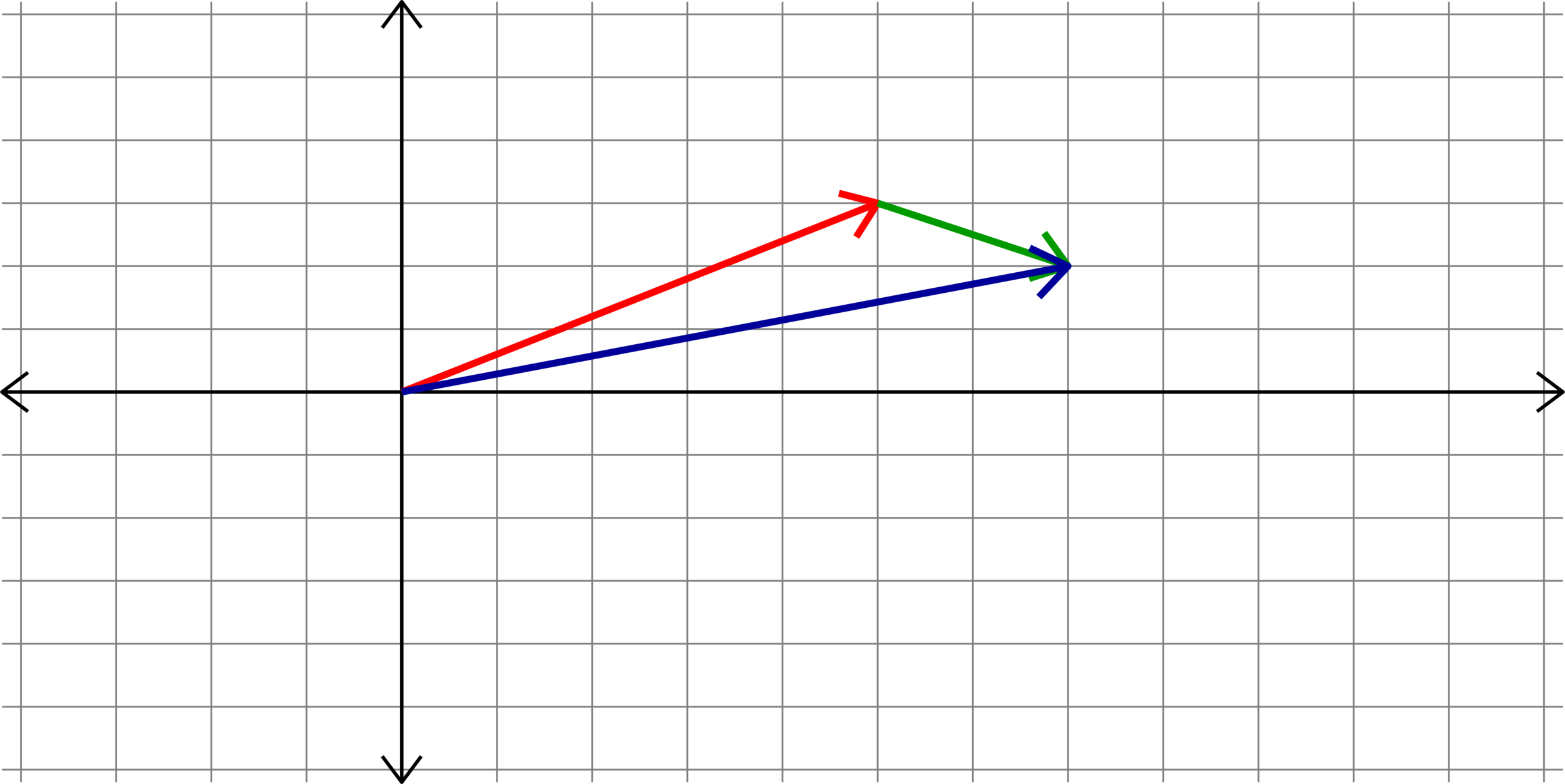
\(\left[\begin{matrix} a_{1}\\ a_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} a_{1}+b_{1}\\ a_{2}+b_{2}\end{matrix}\right]\)
How do we add two vectors?
\(\left[\begin{matrix} a_{1}\\ a_{2}\end{matrix}\right]\)
\(\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right]\)
+ =
\(\left[\begin{matrix} a_{1}+b_{1}\\ a_{2}+b_{2}\end{matrix}\right]\)
Algebra with Vectors and Matrices
Adding vectors:
\(\left[\begin{matrix}2\\ 1\end{matrix}\right] + \left[\begin{matrix}0.5\\ 1\end{matrix}\right] = \left[\begin{matrix}2+0.5\\ 1+1\end{matrix}\right] = \left[\begin{matrix}2.5\\ 2\end{matrix}\right] \)
\(\left[\begin{matrix}2\\ -3\\1\end{matrix}\right] + \left[\begin{matrix}-1.1\\0.5\\ 1\end{matrix}\right] = \left[\begin{matrix}2-1.1\\-3+0.5\\1+1\end{matrix}\right] = \left[\begin{matrix}0.9\\-2.5\\ 2\end{matrix}\right] \)
\(\left[\begin{matrix}a_{1}\\ a_{2}\\ \vdots \\ a_{n}\end{matrix}\right] + \left[\begin{matrix}b_{1}\\ b_{2}\\ \vdots \\ b_{n}\end{matrix}\right] = \left[\begin{matrix}a_{1}+b_{1}\\ a_{2}+b_{2}\\ \vdots \\ a_{n}+b_{n}\end{matrix}\right]\)
In general:

Danger
\(\left[\begin{matrix}2\\ -3\\1\end{matrix}\right] + \left[\begin{matrix}-1.1\\0.5\end{matrix}\right]\)

Vectors in different dimensions cannot be added!
Algebra with Vectors and Matrices
Multiplying vectors by scalars:
\(3\left[\begin{matrix}2\\ -1\end{matrix}\right] = \left[\begin{matrix}3\cdot 2\\ 3\cdot(-1)\end{matrix}\right] = \left[\begin{matrix}6\\ -3\end{matrix}\right] \)
\(-0.2\left[\begin{matrix}-1.2\\0\\3\end{matrix}\right] = \left[\begin{matrix} (-0.2)(-1.2)\\ -0.2\cdot 0\\ -0.2\cdot 3\end{matrix}\right] = \left[\begin{matrix}0.24\\ 0\\ -0.6\end{matrix}\right]\)
\(c\left[\begin{matrix}a_{1}\\ a_{2}\\ \vdots \\ a_{n}\end{matrix}\right] = \left[\begin{matrix}ca_{1}\\ ca_{2}\\ \vdots \\ ca_{n}\end{matrix}\right]\)
In general:
Algebra with Vectors and Matrices
Multiplying matrices and vectors:
\(\left[\begin{matrix} a_{11} & a_{12}\\ a_{21} & a_{22}\end{matrix}\right]\left[\begin{matrix} b_{1}\\ b_{2}\end{matrix}\right] = b_{1}\left[\begin{matrix} a_{11}\\ a_{21}\end{matrix}\right] + b_{2}\left[\begin{matrix}a_{12}\\ a_{22}\end{matrix}\right]\)
\(\left[\begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{matrix}\right]\left[\begin{matrix} b_{1}\\ b_{2}\\b_{3}\end{matrix}\right] = b_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ a_{31}\end{matrix}\right] + b_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ a_{32}\end{matrix}\right] + b_{3}\left[\begin{matrix}a_{13}\\ a_{23}\\ a_{33}\end{matrix}\right]\)
\(\left[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & & a_{2n}\\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{matrix}\right]\left[\begin{matrix} b_{1}\\ b_{2}\\ \vdots\\b_{n}\end{matrix}\right] = b_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{m1}\end{matrix}\right] + b_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{m2}\end{matrix}\right] + \cdots + b_{n}\left[\begin{matrix}a_{1n}\\ a_{2n}\\ \vdots\\ a_{mn}\end{matrix}\right]\)
\(=\left[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1N}\\ a_{21} & a_{22} & & a_{2N}\\ \vdots & & \ddots & \vdots \\ a_{M1} & a_{M2} & \cdots & a_{MN}\end{matrix}\right]\left(\left[\begin{matrix} x_{1}\\ x_{2}\\ \vdots\\x_{N}\end{matrix}\right] + \left[\begin{matrix} y_{1}\\ y_{2}\\ \vdots\\y_{N}\end{matrix}\right]\right)\)
Matrix multiplication is "linear"
\(= \left[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1N}\\ a_{21} & a_{22} & & a_{2N}\\ \vdots & & \ddots & \vdots \\ a_{M1} & a_{M2} & \cdots & a_{MN}\end{matrix}\right]\left[\begin{matrix} x_{1}+y_{1}\\ x_{2}+y_{2}\\ \vdots\\x_{N}+y_{N}\end{matrix}\right]\)
\(= (x_{1}+y_{1})\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{M1}\end{matrix}\right] + (x_{2}+y_{2})\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{M2}\end{matrix}\right] + \cdots + (x_{N}+y_{N})\left[\begin{matrix}a_{1N}\\ a_{2N}\\ \vdots\\ a_{MN}\end{matrix}\right]\)
\(A(x+y)\)
Matrix multiplication is "linear"
\(= (x_{1}+y_{1})\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{M1}\end{matrix}\right] + (x_{2}+y_{2})\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{M2}\end{matrix}\right] + \cdots + (x_{N}+y_{N})\left[\begin{matrix}a_{1N}\\ a_{2N}\\ \vdots\\ a_{MN}\end{matrix}\right]\)
\(= x_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{M1}\end{matrix}\right] + x_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{M2}\end{matrix}\right] + \cdots + x_{N}\left[\begin{matrix}a_{1N}\\ a_{2N}\\ \vdots\\ a_{MN}\end{matrix}\right] \)
\(+ y_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{M1}\end{matrix}\right] + y_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{M2}\end{matrix}\right] + \cdots + y_{N}\left[\begin{matrix}a_{1N}\\ a_{2N}\\ \vdots\\ a_{MN}\end{matrix}\right]\)
\(=Ax+Ay\)
Matrix multiplication is "linear"
Hence, if \(A\) is an \(M\times N\) matrix and \(x,y\in\mathbb{R}^{N}\), then
\[A(x+y)=Ax+Ay.\]
We can also show that if \(A\) is an \(M\times N\) matrix, \(x\in\mathbb{R}^{N}\), and \(c\in\mathbb{R}\), then \[A(cx)=cAx.\]
(Linear) Combinations
\(\left[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & & a_{2n}\\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{matrix}\right]\left[\begin{matrix} b_{1}\\ b_{2}\\ \vdots\\b_{n}\end{matrix}\right] = b_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{m1}\end{matrix}\right] + b_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{m2}\end{matrix}\right] + \cdots + b_{n}\left[\begin{matrix}a_{1n}\\ a_{2n}\\ \vdots\\ a_{mn}\end{matrix}\right]\)
Definition 1. A linear combination of the vectors \(v_{1},v_{2},\ldots,v_{n}\) is a sum of the form
\[a_{1}v_{1}+a_{2}v_{2}+\cdots+a_{n}v_{n}\]
where \(a_{1},a_{2},\ldots,a_{n}\) are scalars.
So, if \(A\) is an \(m\times n\) matrix, and \(\boldsymbol{b}\) is a vector in \(\R^{n}\), then \(A\boldsymbol{b}\) is a (linear) combination of the columns of \(A\).
Moreover, the set \(\{A\boldsymbol{b} : \boldsymbol{b}\in\R^{n}\}\) is the set of all linear combinations of the columns of \(A\).
Column Space
Definition 2. Given a matrix \(A\), the column space of \(A\), written as \(C(A)\), is the set of all combinations of the columns of \(A\). That is, if
\[A=\left[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & & a_{2n}\\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{matrix}\right],\]
then
\[C(A) = \left\{b_{1}\left[\begin{matrix} a_{11}\\ a_{21}\\ \vdots \\ a_{m1}\end{matrix}\right] + b_{2}\left[\begin{matrix}a_{12}\\ a_{22}\\ \vdots\\ a_{m2}\end{matrix}\right] + \cdots + b_{n}\left[\begin{matrix}a_{1n}\\ a_{2n}\\ \vdots\\ a_{mn}\end{matrix}\right] : b_{1},b_{2},\ldots,b_{n}\in\R\right\}\]
More compactly, if \(A\) has \(n\) columns, then
\[C(A) = \{A\boldsymbol{b} : \boldsymbol{b}\in\R^{n}\}.\]
Subspaces
Definition 3. A subspace of \(\R^N\) is a nonempty set \(V\subset\R^N\) with the following two properties:
- If \(v,w\in V\), then \(v+w\in V\).
- If \(v\in V\) and \(a\in\R\), then \(av\in V\).
Let \(A\) be an \(M\times N\) matrix. If \(v,w\in C(A)\), then \(v=Ab\) for some \(b\in\R^N\) and \(w=Ac\) for some \(c\in\R^{N}\). Hence
\[v+w = Ab+Ac = A(b+c)\in C(A).\]
So, Property 1 of Definition 3 is satisfied. Similarly, if \(a\in\R\), then
\[aAb = A(ab),\]
and since \(ab\in\R^{N}\) we see that \(aAb\in C(A).\) Thus, Property 2 of Definition 3 is satisfied. Hence \(C(A)\) is a subspace of \(\R^M\).
Let \(A\) be an \(M\times N\) matrix.
Let \(A\) be an \(M\times N\) matrix. If \(v,w\in C(A)\), then \(v=Ab\) for some \(b\in\R^N\) and \(w=Ac\) for some \(c\in\R^{N}\).
Let \(A\) be an \(M\times N\) matrix. If \(v,w\in C(A)\), then \(v=Ab\) for some \(b\in\R^N\) and \(w=Ac\) for some \(c\in\R^{N}\). Hence
\[v+w = Ab+Ac = A(b+c)\in C(A).\]
So, Property 1 of Definition 3 is satisfied.
Bases
Definition 4. Let \(V\) be a subspace. A basis for \(V\) is a collection of vectors \(\{v_{1},v_{2},\ldots,v_{r}\}\subset V\) with the following properties:
- If \(v\in V\), then there are scalars \(a_{1},\ldots,a_{r}\) such that \[a_{1}v_{1} + a_{2}v_{2} + \cdots + a_{r}v_{r} = v\]
- If \[b_{1}v_{1}+b_{2}v_{2}+\cdots+b_{r}v_{r} = 0\] for some scalars \(b_{1},\ldots,b_{r}\), then \(b_{1}=b_{2}=\cdots=b_{r}=0\).
If a sequence of vectors in \(V\) satisfy Property 1, then we say that \(\{v_{1},v_{2},\ldots,v_{r}\}\) spans \(V\).
If a sequence of vectors satisfy Property 2, then we say that \(\{v_{1},v_{2},\ldots,v_{r}\}\) is linearly independent.
Linear Dependence
Definition 5. Let \(v_{1},v_{2},\ldots,v_{r}\) be vectors in \(\R^M\). If there are scalars \(a_{1},a_{2},\ldots,a_{r}\) at least one of which is not zero such that \[a_{1}v_{1}+a_{2}v_{2}+\cdots+a_{r}v_{r} = 0,\] then we say that the set of vectors \(\{v_{1},v_{2},\ldots,v_{r}\}\) is (linearly) dependent.
Examples. 1) \(\left[\begin{matrix}1\\ 0\end{matrix}\right]\) and \(\left[\begin{matrix}2\\ 0\end{matrix}\right]\) are dependent since \(2\left[\begin{matrix}1\\ 0\end{matrix}\right]+(-1)\left[\begin{matrix}2\\ 0\end{matrix}\right]=0\)
2) \(\left[\begin{matrix}1\\ 0\\ -1\end{matrix}\right],\left[\begin{matrix}1\\ 1\\ 2\end{matrix}\right],\left[\begin{matrix}2.5\\ 1\\ 0.5\end{matrix}\right]\) are dependent since \[3\!\left[\begin{matrix}1\\ 0\\ -1\end{matrix}\right]\!\!+2\!\left[\begin{matrix}1\\ 1\\ 2\end{matrix}\right]\!-2\!\left[\begin{matrix}2.5\\ 1\\ 0.5\end{matrix}\right]\! =\! \left[\begin{matrix} 0\\ 0\\ 0\end{matrix}\right] \]
3) The set containing just the zero vector is dependent, since the zeros vector is a linear combination of itself. (What does a linear combination of a single vector look like?)
A basis for \(C(A)\)
Let \(v_{1},v_{2},\ldots,v_{N}\) be the columns of the matrix \(A\).
Run the following pseudocode to obtain a basis for \(C(A)\) stored in the variable "Basis"
j=0; % Set counter to zero
Basis=[]; % Initialize an empty list
while j<N
j=j+1;
if [Basis v_j] is independent
Basis=[Basis v_j];
% If the new list is independent,
% then include v_j in the list.
end
endExample. Use the above algorithm to find a basis for \(C(A)\) where \(A = \left[\begin{matrix} 0 & 1 & 2 & 3\\ 0 & 4 & 5 & 6\\ 0 & 7 & 8 & 9\end{matrix}\right]\)
Is \(\left[\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}\right]\) independent?
Basis =
NO!
Is \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\) independent?
YES!
\(()\)
\(\left(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\right)\)
Are \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right],\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right]\) independent?
YES!
\(\left(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right], \left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right]\right)\)
Are \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right],\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right],\left[\begin{matrix} 3 \\ 6 \\ 9\end{matrix}\right]\) independent?
Is \(\left[\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}\right]\) independent?
\(()\)
\(()\)
\(()\)
\(()\)
Is \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\) independent?
Is \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\) independent?
YES!
Are \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right],\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right]\) independent?
YES!
Are \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right],\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right]\) independent?
\(\left(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\right)\)
\(\left(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]\right)\)
Are \(\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right],\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right],\left[\begin{matrix} 3 \\ 6 \\ 9\end{matrix}\right]\) independent?
NO!
\(-1\left[\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}\right]+2\left[\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}\right]-\left[\begin{matrix} 3 \\ 6 \\ 9\end{matrix}\right]=0\)
This is our basis for \(C(A)\)!
Definitions you must know!
- \(\mathbb{R}^{N}\) is the set of all \(N\times 1\) column vectors.
- Multiplying matrices ("internal" dimensions must agree)
- Linear combinations
- The column space of a matrix \(A\), denoted \(C(A)\)
- Subspace of \(\mathbb{R}^{N}\)
- Basis of a subspace
- Span of a set of vectors
- Linear independence/dependence of a set of vectors