Day 28:
Applications of SVD
Example continued. Let \(\displaystyle{B = \begin{bmatrix} 2 & -1\\ 2 & 1\end{bmatrix}.}\)
\(B(\text{blue vector}) = \text{red vector}\)
\(\text{blue vector}\)
\(\text{red vector}\)
The blue vectors go through all vectors of length \(1\).

Proposition. If \(S\) is a positive semidefinite \(n\times n\) matrix, then the maximum value of \(\frac{\|Sx\|}{\|x\|}\) for all \(x\in\R^{n}\setminus\{0\}\) is the largest eigenvalue \(\lambda_{1}\) of \(S\). This maximum is attained when \(x\) is an eigenvector of \(S\) associated with \(\lambda_{1}\).
Proof. By the Spectral theorem there is an orthonormal basis of eigenvectors \(\{v_{1},\ldots,v_{n}\}\) of \(S\) with associated eigenvalues \(\lambda_{1}\geq \lambda_{2}\geq\cdots \geq \lambda_{n}\geq 0.\) Let \(Q\) be the matrix with columns \(v_{1},\ldots,v_{n}\), then \(Q\) is an orthogonal matrix, and hence if \(x\in\R^{n}\), then \[\|x\|^{2} = x^{\top}x = x^{\top}QQ^{\top}x = x^{\top}\left(\sum_{i=1}^{n}v_{i}v_{i}^{\top}\right)x = \sum_{i=1}^{n}x^{\top}v_{i}v_{i}^{\top}x = \sum_{i=1}^{n}(v_{i}^{\top}x)^2.\] Let \(\Lambda\) be the diagonal matrix with \(\lambda_{1},\dots,\lambda_{n}\) on the diagonal, so that \(S=Q\Lambda Q^{\top}\), then \[\|Sx\|^{2} = x^{\top}S^{\top}Sx = x^{\top}Q\Lambda^{2}Q^{\top}x = x^{\top}\left(\sum_{i=1}^{n}\lambda_{i}^{2}v_{i}v_{i}^{\top}\right)x = \sum_{i=1}^{n}\lambda_{i}^{2}(v_{i}^{\top}x)^2 \]
\[\leq \sum_{i=1}^{n}\lambda_{1}^{2}(v_{i}^{\top}x)^2 = \lambda_{1}^{2}\sum_{i=1}^{n}(v_{i}^{\top}x)^2 = \lambda_{1}^{2}\|x\|^{2}\]
Hence, for any \(x\in\R^{n}\) we have \(\|Sx\|^{2}\leq \lambda_{1}^{2}\|x\|^{2}.\) If \(x\neq 0\) then we can divide both sides by \(\|x\|^{2}\) and take the square root of both sides and we have \[\frac{\|Sx\|}{\|x\|}\leq \lambda_{1}.\]
Finally, note that
\[\frac{\|Sv_{1}\|}{\|v_{1}\|} = \|\lambda_{1}v_{1}\| = \lambda_{1}.\]
\(\Box\)
Corollary. If \(A\) is an \(m\times n\) matrix, then the maximum value of \(\frac{\|Ax\|}{\|x\|}\) for all \(x\in\R^{n}\) is the largest singular value \(\sigma_{1}\). The maximum value is attained at the right singular vector \(v_{1}\).
Proof. Set \(S=A^{\top}A\). Since \(S\) is positive semidefinite, there is a positive semidefinite matrix \(\sqrt{S}\) such that \((\sqrt{S})^2=S\). The largest eigevalue of \(\sqrt{S}\) is \(\sigma_{1}\).
\[\|Ax\|^{2} = x^{\top}Sx = x^{\top}\sqrt{S}^{\top}\sqrt{S}x = \|\sqrt{S}x\|^{2}.\]
Hence, for \(x\neq 0\) we have
\[\frac{\|Ax\|}{\|x\|} = \frac{\|\sqrt{S}x\|}{\|x\|}\]
The maximum over all \(x\in\R^{n}\setminus\{0\}\) is \(\sigma_{1}\) and this maximum is attained at the eigenvector of \(\sqrt{S}\) with eigenvalue \(\sigma_{1}\), that is, the right singular vector \(s_{1}\). \(\Box\)
Hence, if \(A\) is any matrix, and the singular values of \(A\) are \(\sigma_{1}\geq \sigma_{2}\geq \ldots\geq \sigma_{p},\) then we have
\[\max_{x\in\R^{n}\setminus\{0\}}\frac{\|Ax\|}{\|x\|} = \sigma_{1}\]
Note that
\[\frac{\|Ax\|}{\|x\|} = \tfrac{1}{\|x\|}\|Ax\| = \left\|\tfrac{1}{\|x\|}Ax\right\| = \left\|A\left(\tfrac{x}{\|x\|}\right)\right\|.\]
Hence, we might as well only look at vectors \(x\) with norm \(1\):
\[\max_{\substack{x\in\R^{n}\\ \|x\|=1}}\|Ax\| = \sigma_{1}\]
\(x\) scaled to have norm \(1\)
Similarly,
\[\max_{\substack{x\in\R^{n}\setminus\{0\}\\ v_{1}^{\top}x=0}}\frac{\|Ax\|}{\|x\|} = \sigma_{2}\]
And the max is achieved at the right singular vector \(v_{2}\). And so on...
Example continued. Let \(\displaystyle{B = \begin{bmatrix} 2 & -1\\ 2 & 1\end{bmatrix}.}\)
\(B(\text{blue vector}) = \text{red vector}\)
\(\text{blue vector}\)
\(\text{red vector}\)
The blue vectors go through all vectors of length \(1\).


Example continued. Let \(\displaystyle{B = \begin{bmatrix} 3 & -1\\ -1 & 2\end{bmatrix}.}\)
\(B(\text{blue vector}) = \text{red vector}\)
\(\text{blue vector}\)
\(\text{red vector}\)
The blue vectors go through all vectors of length \(1\).

Example continued. Let \(\displaystyle{B = \begin{bmatrix} 3 & -1\\ -1 & 2\end{bmatrix}.}\)
\(B(\text{blue vector}) = \text{red vector}\)
\(\text{blue vector}\)
\(\text{red vector}\)
The blue vectors go through all vectors of length \(1\).

Examples. Orthgonal matrices: If \(Q\) is an orthogonal matrix, then a singular value decomposition of \(Q\) would be
\[Q = QII.\]
This means that the singular values of \(Q\) are all \(1\). The right singular vectors of \(Q\) are the standard basis vectors, and the left singular vectors of \(Q\) are the columns of \(Q\).
Positive semidefinite matrices: If \(S\) is positive semidefinite, then there is an orthogonal matrix \(Q\) and a diagonal matrix \(\Lambda\) with entries \(\lambda_{1}\geq \lambda_{2}\geq\ldots\geq 0\) such that
\[S = Q\Lambda Q^{\top}.\]
This means that the singular values of \(S\) are all \(\lambda_{1},\lambda_{2},\ldots\). The left singular vectors and the right singular vectors of \(S\) are the columns of \(Q\), that is, they are the orthonormal basis of eigenvectors with corresponding eigenvalues \(\lambda_{1},\lambda_{2},\ldots\).
Examples. Symmetric Matrices: If \(A\in\mathbb{R}^{n\times n}\) is a symmetric matrix, then there is an orthogonal matrix \(Q\) and a diagonal matrix \(\Lambda\) such that
\[A=Q\Lambda Q^{\top}.\]
This is not necessarily a singular value decomposition of \(A\), since the entries in \(\Lambda\) are not necessarily nonnegative!
However, if we compute
\[A^{\top}A = A^2= Q\Lambda^{2}Q^{\top},\]
then we see that the columns of \(Q\), which are the eigenvectors of \(A,\) are the right singular vectors of \(A\). The singular values of \(A\) are the square roots of the entries on the diagonal of \(\Lambda^{2}\). That is, the singular values of \(A\) are the absolute values of the eigenvalues of \(A\).
Finally, given a right singular vector \(v\) with singular value \(|\lambda|,\) we see that the corresponding left singular vector is \[u = \frac{Av}{|\lambda|} = \frac{\lambda v}{|\lambda|} = \operatorname{sign}(\lambda)v.\]
Matrix Norms
For a vector \(x\in\R^{n}\) there is one natural way to define the norm or length: \(\|x\| = \sqrt{x^{\top}x}.\)
For an \(n\times m\) matrix \(A\) there are a few ways we commonly define the norm of \(A\):
Definition. Given an \(m\times n\) matrix \(A\) with singular values \(\sigma_{1}\geq \sigma_{2}\geq\ldots\geq \sigma_{r}\) we define the following three norms:
The spectral norm: \(\displaystyle{\|A\|_{2} = \max_{x\in\R^{n}\setminus\{0\}}\frac{\|Ax\|}{\|x\|} = \sigma_{1}}\)
The Frobenius norm: \(\displaystyle{\|A\|_{F} = \sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}+\cdots+\sigma_{r}^{2}}}\)
The nuclear norm: \(\displaystyle{\|A\|_{N} = \sigma_{1}+\sigma_{2}+\cdots+\sigma_{r}}\)
For each norm we can define a different distance between matrices. We say that the distance between \(A\) and \(B\) is \(\|A-B\|\)
Matrix Norms
Examples. Orthgonal matrices: If \(Q\) is an \(n\times n\) orthogonal matrix, then \[\|Q\|_{2} = 1,\quad\|Q\|_{F} = \sqrt{n},\quad\text{and}\quad \|Q\|_{N} = n\]
Positive semidefinite matrices: If \(S\) is positive semidefinite, with eigenvalues \(\lambda_{1}\geq \lambda_{2}\geq\ldots\geq 0\), then
\[\|S\|_{2} = \lambda_{1}\] \[\|S\|_{F} = \sqrt{\sum_{i}\lambda_{i}^{2}}\]\[\|S\|_{N} = \sum_{i}\lambda_{i}\]
Let \(A\) be an \(m\times n\) matrix with singular value decomposition
\[A = \sigma_{1}u_{1}v_{1}^{\top} + \sigma_{2}u_{2}v_{2}^{\top} + \cdots + \sigma_{r}u_{r}v_{r}^{\top}\]
where \(r=\text{rank}(A).\)
For each \(k\leq r\) we define the matrix
\[A_{k} = \sigma_{1}u_{1}v_{1}^{\top} + \sigma_{2}u_{2}v_{2}^{\top} + \cdots + \sigma_{k}u_{k}v_{k}^{\top}\]
That is, if \(B\) is any \(m\times n\) matrix with rank \(k\), then
\[\|A-A_{k}\|\leq \|A-B\|\]
We will show that \(A_{k}\) is the closest rank \(k\) matrix to \(A\) among all rank \(k\) matrices.
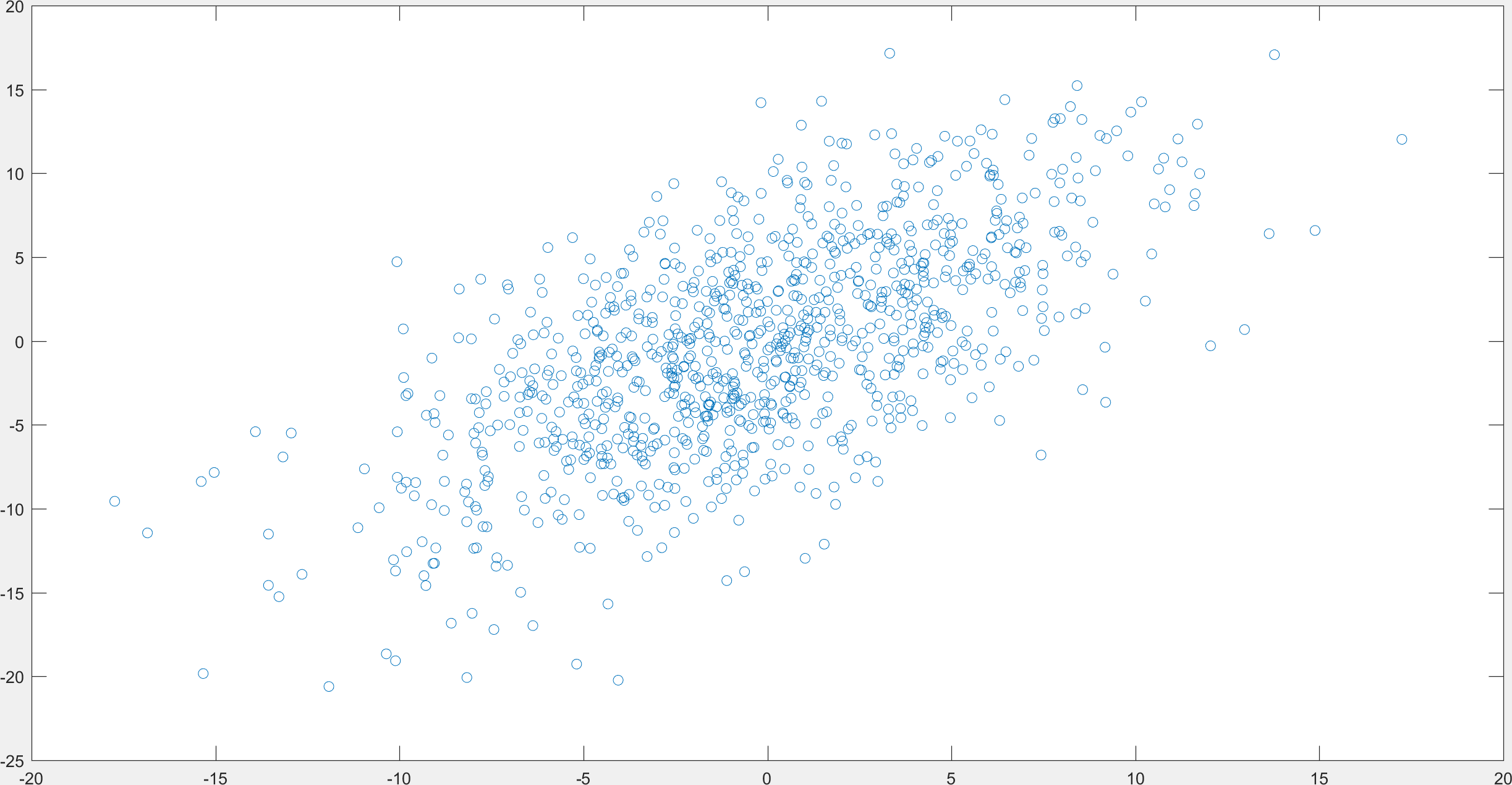
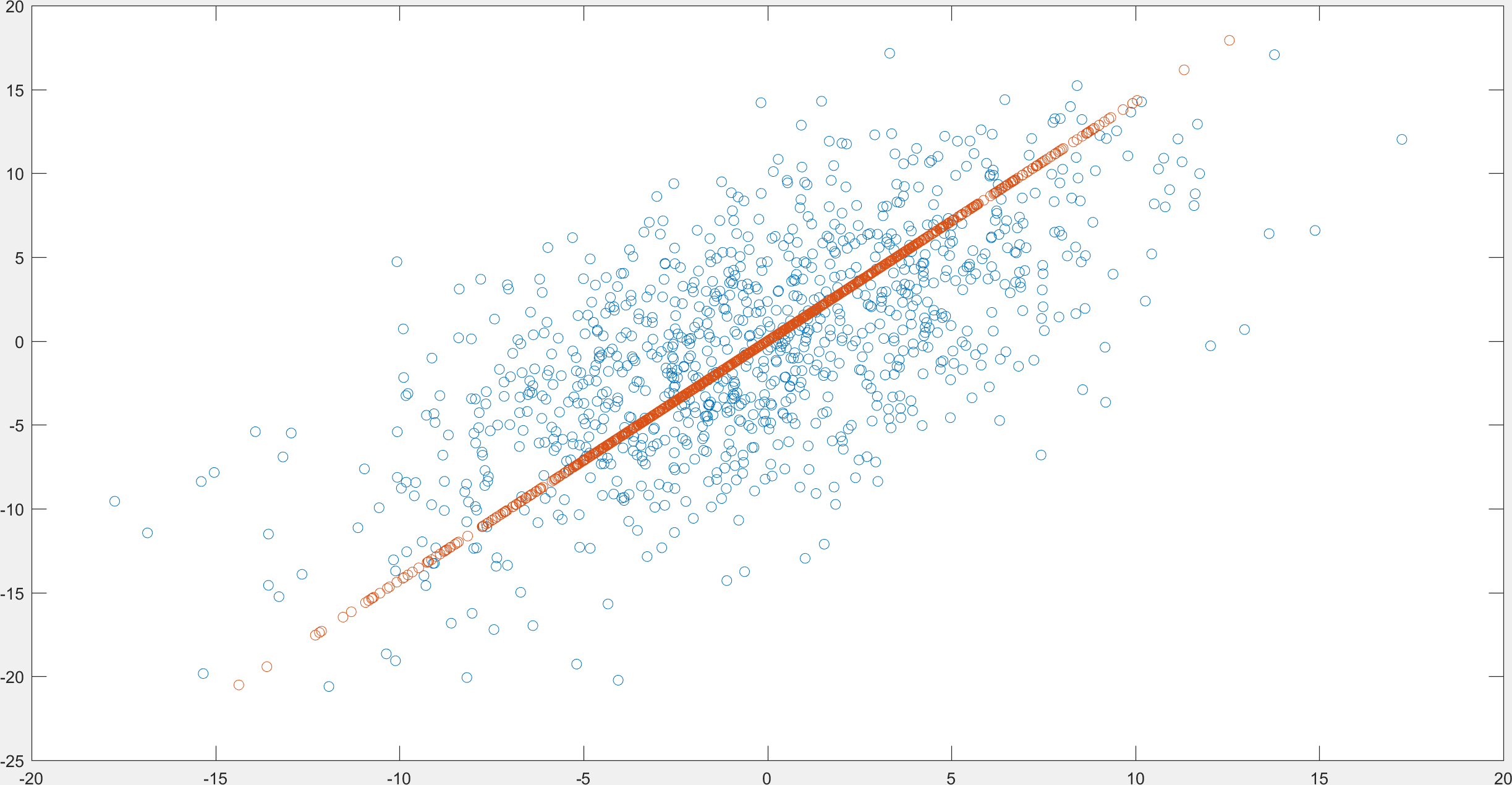
\(A = \begin{bmatrix} x_{1} & x_{2} & \cdots & x_{N}\\ y_{1} & y_{2} & \cdots & y_{N}\end{bmatrix}\)
\(A_{1} = \begin{bmatrix} c_{1}a & c_{2}a & \cdots & c_{N}a\\ c_{1}b & c_{2}b & \cdots & c_{N}b\end{bmatrix}\)
is the closest rank 1 matrix to \(A\).
Example