Lecture 2:
Manipulating inequalities
Proposition 2. If \(a>b\) and \(c\in\R\), then \(a+c>b+c\).
Proposition 3. If \(a>b\) and \(c>0\), then \(ac>bc\).
How do we use Propositions 2 and 3?
Let's say we know that \(x\) is a number such that \(x>4\).
From Proposition \(2\) we see that \(x-1>3\).
From Proposition \(3\) we see that \(2x-2>6\).
If \(x\) is a real number such that \(-1<x<3\), then what can we say about the number \(3x-5\)?
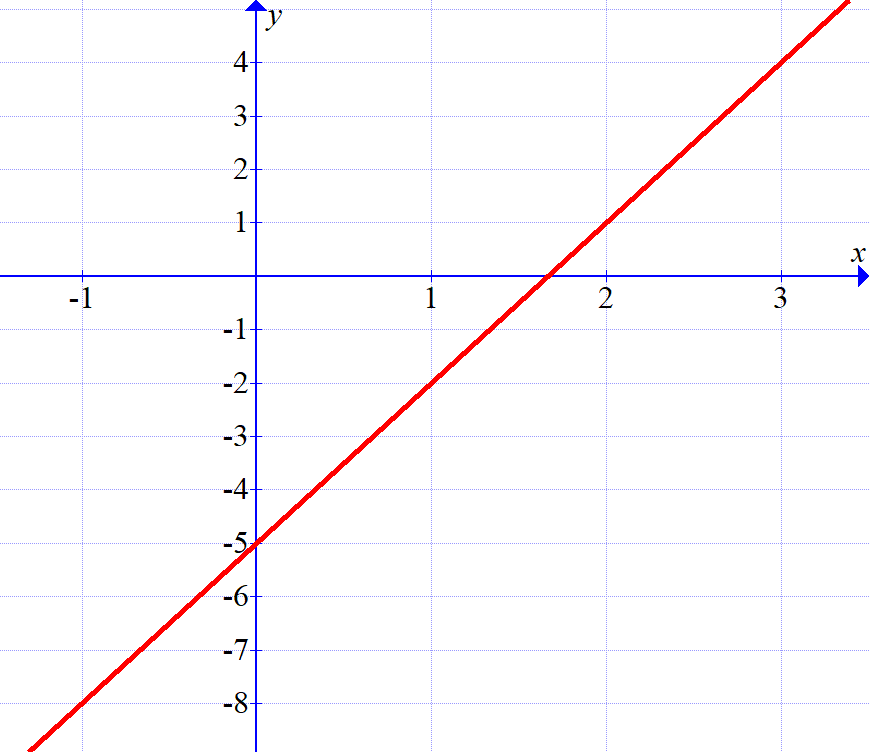
\(y=3x-5\)
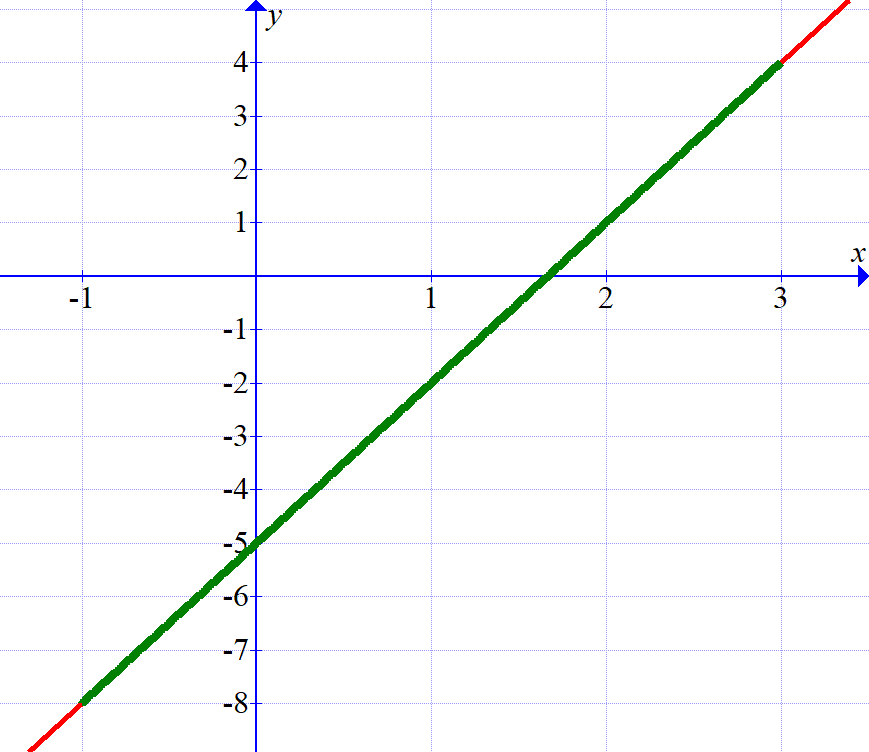
From the picture, it appears that \(-8<3x-5<4\), but how do we prove it?
Proposition. If \(-1<x<3\), then \(-8<3x-5<4\).
Proof. Assume \(-1<x<3\). From the assumption that \(x>-1\) we see that \(3x>-3\), and hence \(3x-5>-8\). From the assumption that \(x<3\) we see that \(3x<9\), and hence \(3x-5<4\). Putting these together we obtain
\[-8<3x-5<4.\ \Box\]
These last two propositions do most of what we need when working with inequalities:
Here is an example: Assume \(1<x<2\). How small can \(-2x^2+2x-4\) be?
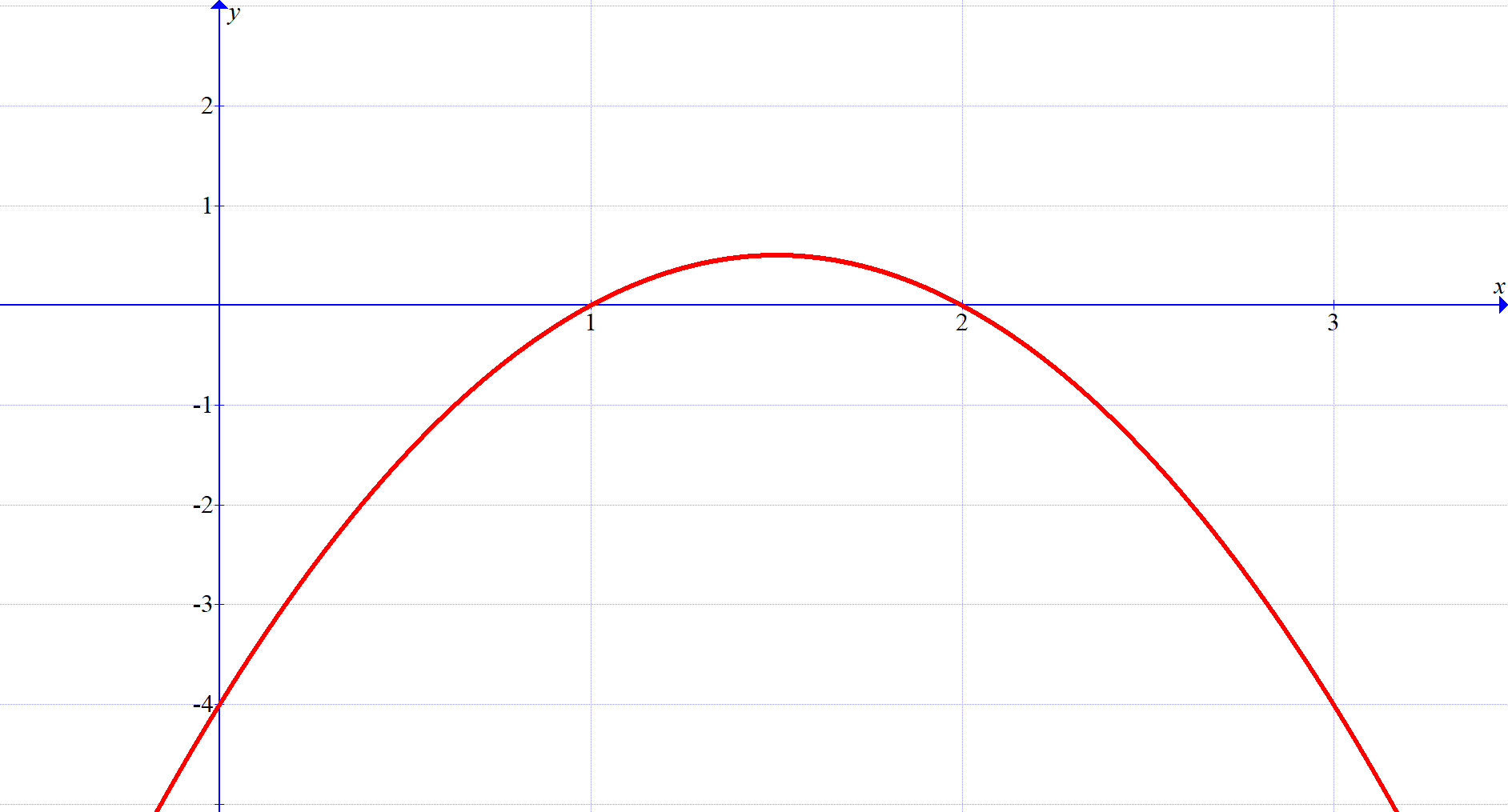
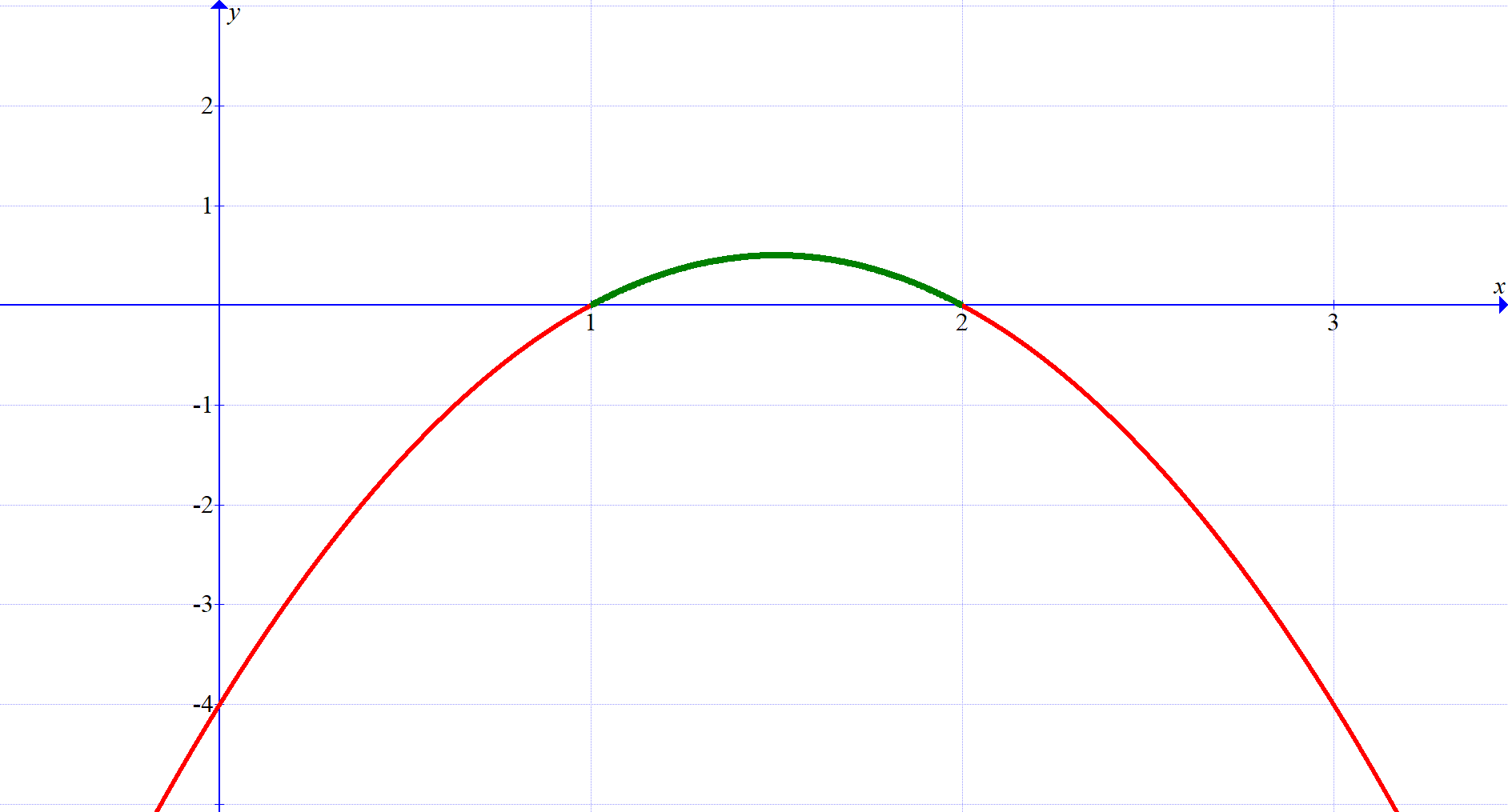
\(y=-2x^2+2x-4\)
Here is an example: Assume \(1<x<2\). How small can \(-2x^2+2x-4\) be?
\[x>1\quad\Rightarrow\quad 2x>2\quad\text{multiplying both sides by } 2\]
\[\quad\Rightarrow\quad 2x-2>0\quad\text{adding \(-2\) to both sides}\]
\[x<2\quad\Rightarrow\quad 0<2-x\quad\text{adding \(-x\) to both sides}\]
Putting these two inequalities together we have
\[2x-2>0\quad\text{and}\quad2-x>0\quad\Rightarrow\quad (2x-2)(2-x)>0\]
since positive numbers are closed under multiplication.
Multiplying this out we see that
\[-2x^2+2x-4>0.\]
A common pitfall
Assume \(x>5\). What can we say about \(\dfrac{1}{x-2}\)?
\[x>5\quad\Rightarrow\quad x-2>3\quad\text{adding \(-2\) to both sides}\]
\[\quad\Rightarrow\quad \frac{1}{x-2}>\frac{1}{3}\quad\text{taking the reciprocal of both sides}\]
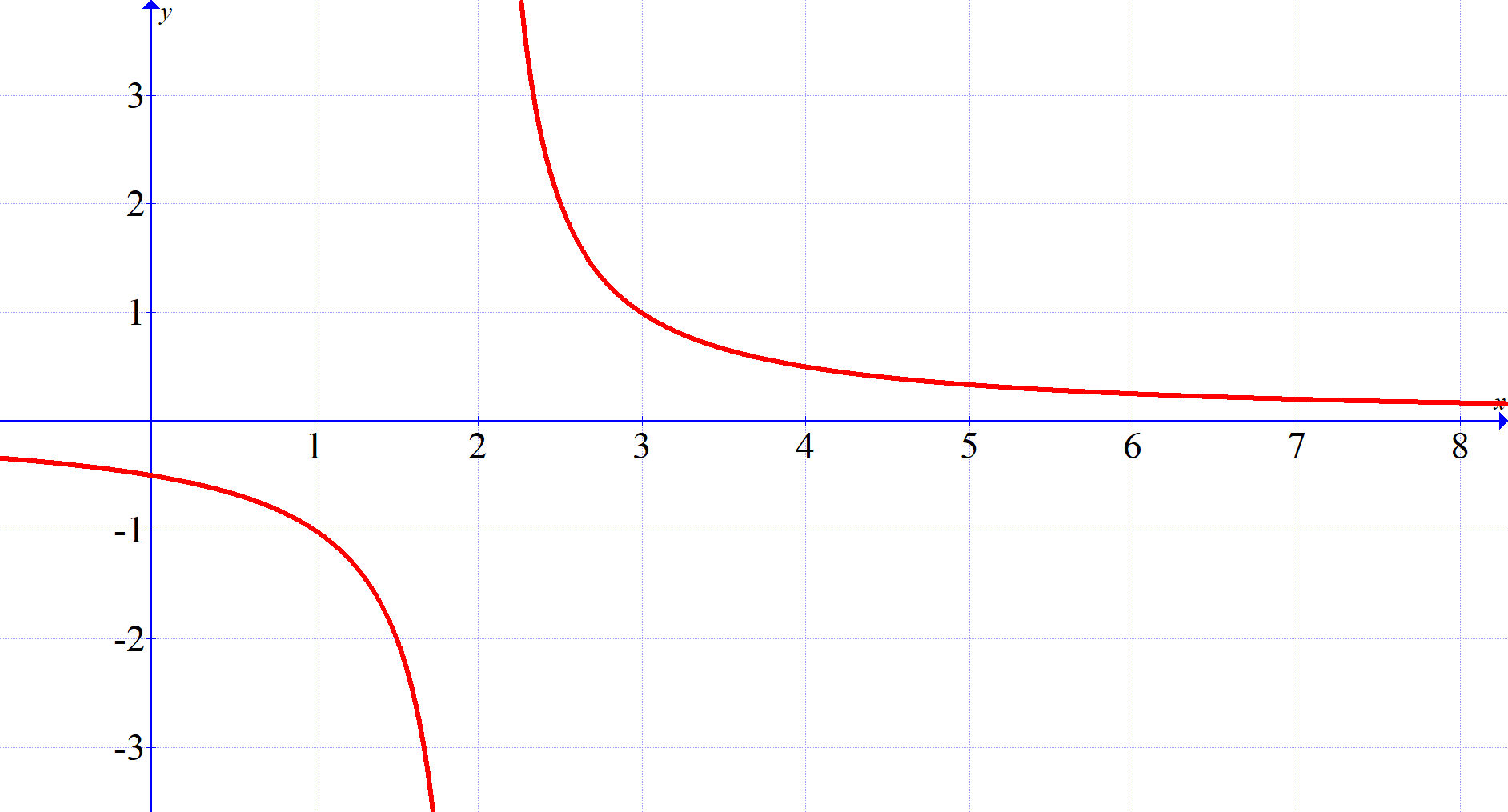
\(y=\dfrac{1}{x-2}\)
A common pitfall (avoided)
Assume \(x>5\). What can we say about \(\dfrac{1}{x-2}\)?
\[x>5\quad\Rightarrow\quad x-2>3\quad\text{adding \(-2\) to both sides}\]
\[x-2>3\quad\Rightarrow\quad 1>\frac{3}{x-2}\quad\text{multiplying both sides by } \frac{1}{x-2}\]
From this we see that \(x-2\) is positive, and hence so is \(\frac{1}{x-2}\) (why?).
Finally, we multiply both sides by \(\frac{1}{3}\) and we see that
\[\frac{1}{3}>\frac{1}{x-2}\]
A common pitfall (avoided)
\[\frac{1}{3}>\frac{1}{x-2}\]
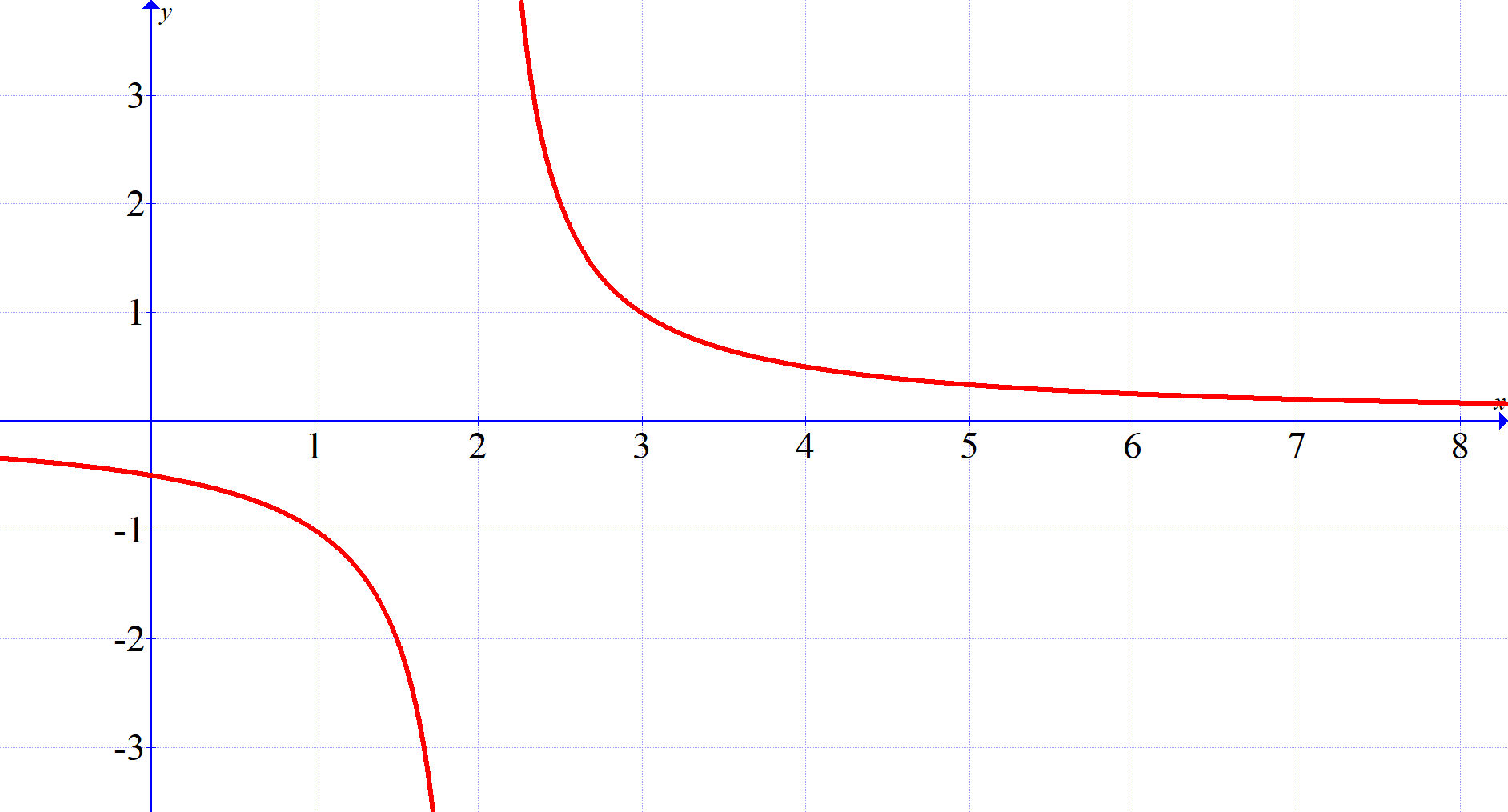
\(y=\dfrac{1}{x-2}\)
Prove the following:
If \(x<3\), then \(\dfrac{2}{4-x}<2\).
Proof. Assume \(x<3\). Adding \(-x\) we obtain \(0<3-x\). Adding \(1\) we see that \(4-x>1\). Note that \(4-x\) is positive, and hence \(\frac{1}{4-x}\) is also positive. Multiplying both sides of \(4-x>1\) by \(\frac{1}{4-x}\) we see that
\[1>\frac{1}{4-x}.\]
Finally, multiplying by \(2\) yields
\[2>\frac{2}{4-x}\]
as desired. \(\Box\)