Lecture 7:
The triangle inequality
The Triangle Inequality
Theorem 2.2.3 (The Triangle Inequality) If \(a\) and \(b\) are real numbers, then \(|a+b|\leq |a|+|b|\).
Proof. From Theorem 2.2.2(d) we see that \(-|a|\leq a\leq |a|\). Adding \(b\), we obtain
\[-|a|+b\leq a+b\leq |a|+b.\]
Since \(b\leq |b|\), we see that \(|a|+b\leq |a|+|b|,\) and hence
\[a+b\leq |a|+|b|.\]
Now, since \(-|b|\leq b\) we see that \(-|a|-|b|\leq -|a|+b\), and hence
\[-|a|-|b|\leq a+b.\]
Putting these two inequalities together we have
\[-(|a|+|b|)\leq a+b\leq |a|+|b|.\]
By Theorem 2.2.2(c) we conclude that
\[|a+b|\leq |a|+|b|.\ \Box\]
Application of the triangle inequality:
Proposition 1. If \(|x-1|<\frac{1}{2}\) and \(|y-1|<\frac{1}{2}\), then \(|x-y|<1\).
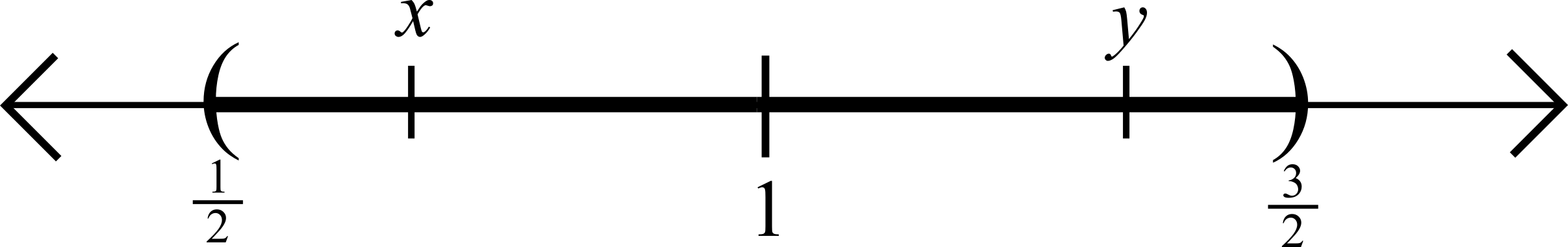
Proof. Suppose \(x\) and \(y\) are two real numbers such that \(|x-1|<\frac{1}{2}\) and \(|y-1|<\frac{1}{2}\). By the triangle inequality
\[|x-y| = |(x-1)+(1-y)|\leq |x-1|+|y-1|<\frac{1}{2}+\frac{1}{2}=1.\ \Box\]
The Reverse Triangle Inequality
Theorem 2.2.4(a). (The Reverse Triangle Inequality) If \(a\) and \(b\) are real numbers, then \(\big||a|-|b|\big|\leq |a+b|\).
Proof. Let \(a\) and \(b\) be real numbers. By the Triangle Inequality we have
\[|a| = |a+b+(-b)|\leq |a+b|+|-b|=|a+b|+|b|.\]
Adding \(-|b|\) to both sides we have
\[|a|-|b|\leq |a+b|.\]
The exact same proof with \(a\) and \(b\) swapped give us
\[-\big(|a|-|b|\big) = |b|-|a|\leq |a+b|.\]
Putting together these last two inequalities, we deduce that
\[\big||a|-|b|\big|\leq |a+b|.\ \Box\]
Proposition. If \(|x-3|\geq 2\), then \(|x-2|\geq 1\).
Proof. Assume \(x\) is a number satisfying the inequality \(|x-3|\geq 2\). By the (Reverse) Triangle Inequality we see that
\[|x-2| = |(x-3)+1|\geq |x-3|-1\geq 2-1 = 1.\ \Box\]
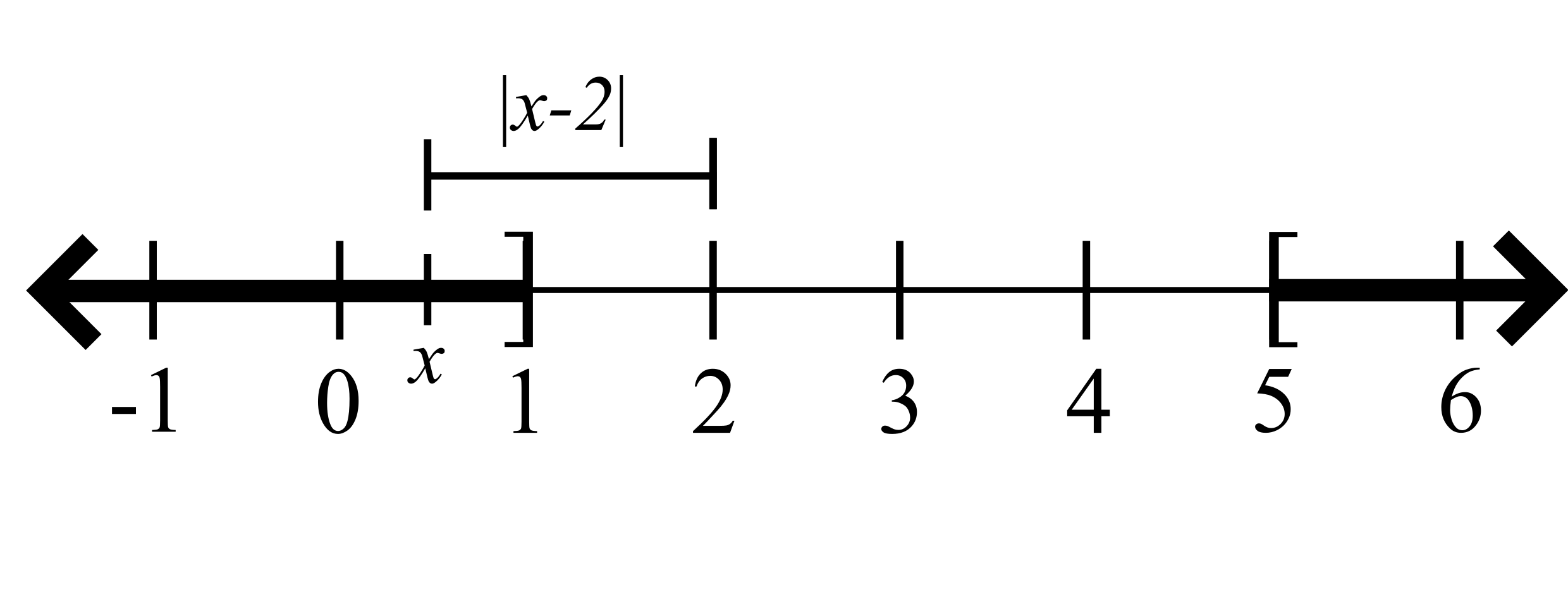
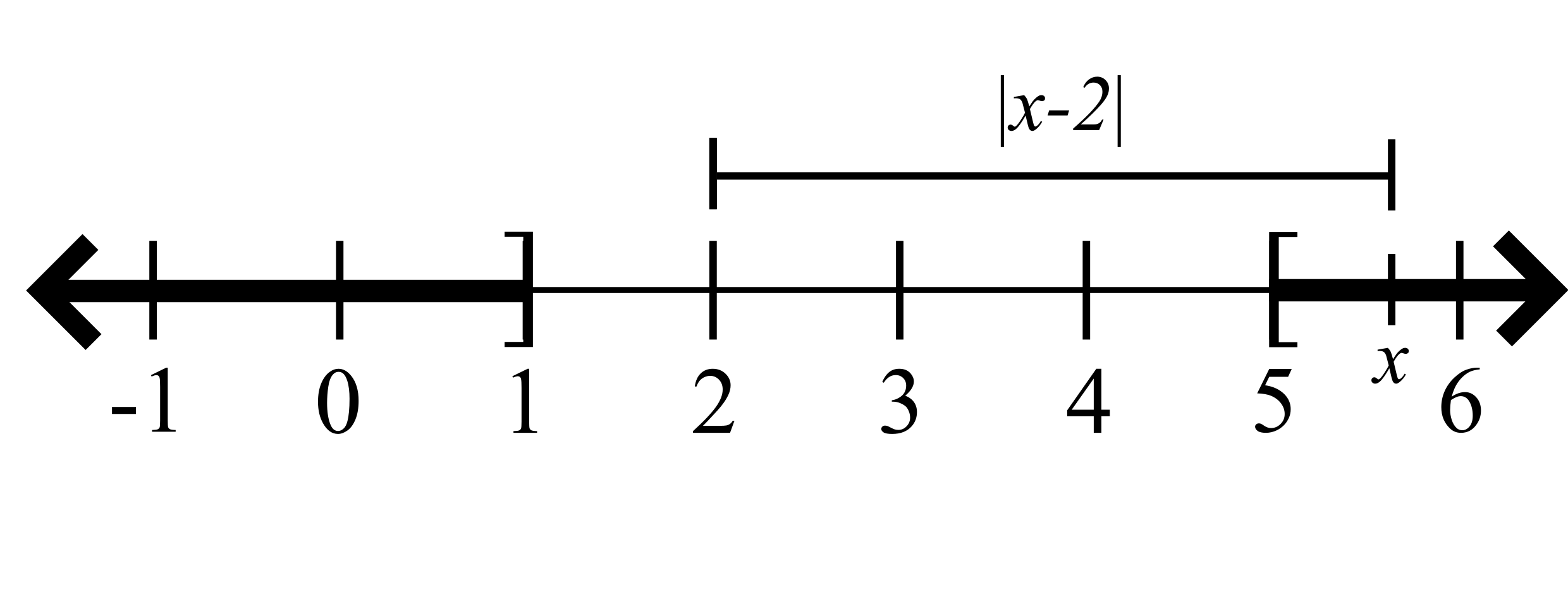
Practice problem:
Prove the following Corollary of the Triangle Inequality:
Corollary 2.2.4 (b) If \(a,b\in\R\), then \(|a-b|\leq |a| + |b|\).
End Lecture 7
Read Section 2.2 again
Proof. By the Triangle inequality
\[|a-b| = |a+(-b)|\leq |a| + |-b| = |a|+|b|.\ \Box\]