Compatable Orthobiangular Tight Frames
John Jasper
joint work w/ Matthew Fickus and Tyler J. Myers
Costructive Functions 2025

https://slides.com/johnjasper/shanks2025/

The views expressed in this talk are those of the speaker and do not reflect the official policy
or position of the United States Air Force, Department of Defense, or the U.S. Government.
Support
Disclaimer
the "building blocks": COBTFs
new equiangular tight frames
Outline
finding vectors maximally "spread out"
Background
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]
Measuring how "spread out" vectors are
\[\mu(\Phi) = \cos(\theta)\]
\(\mu(\Phi) = \cos(\theta)\)??
\(\mu(\Phi) = \cos(\theta)\)
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]
Minimizing coherence
between vectors
\(\Updownarrow\)
Maximizing min. angle
between lines

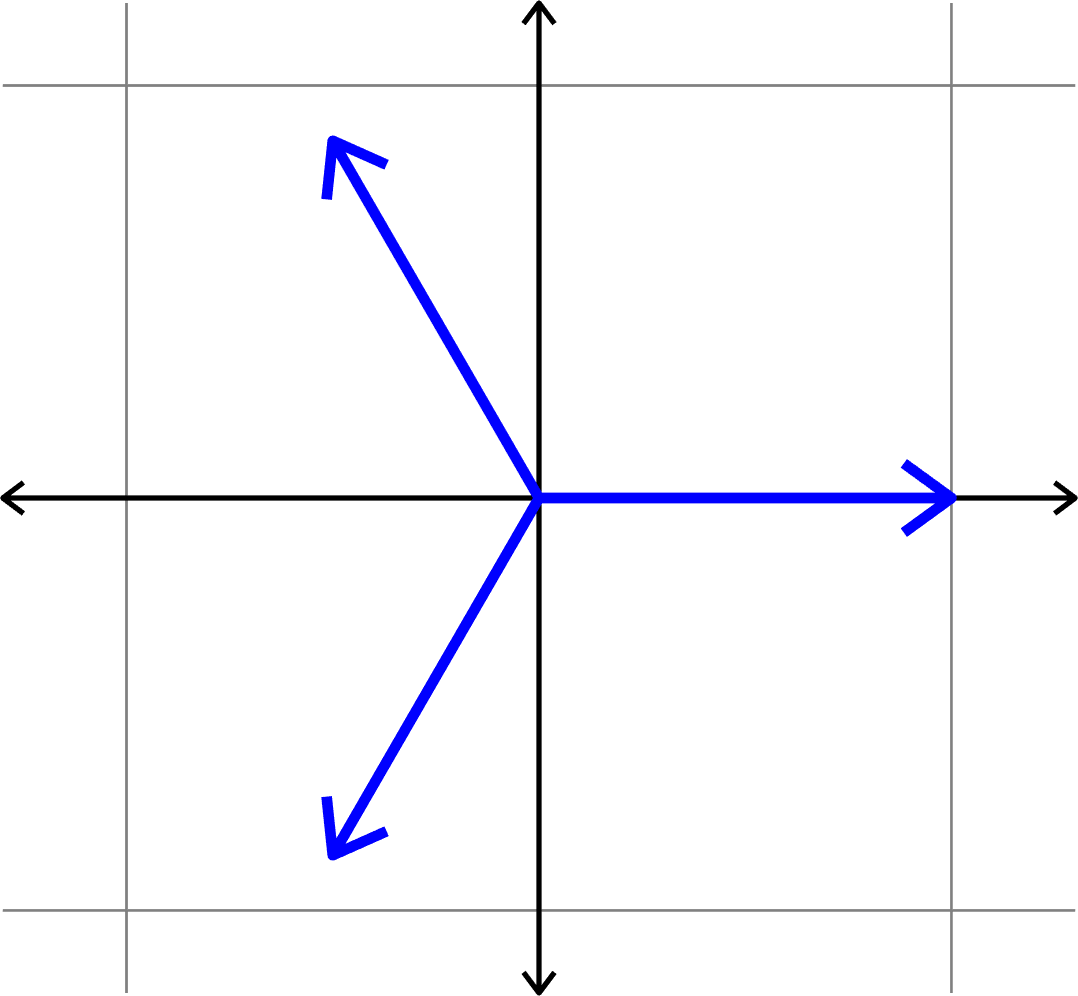
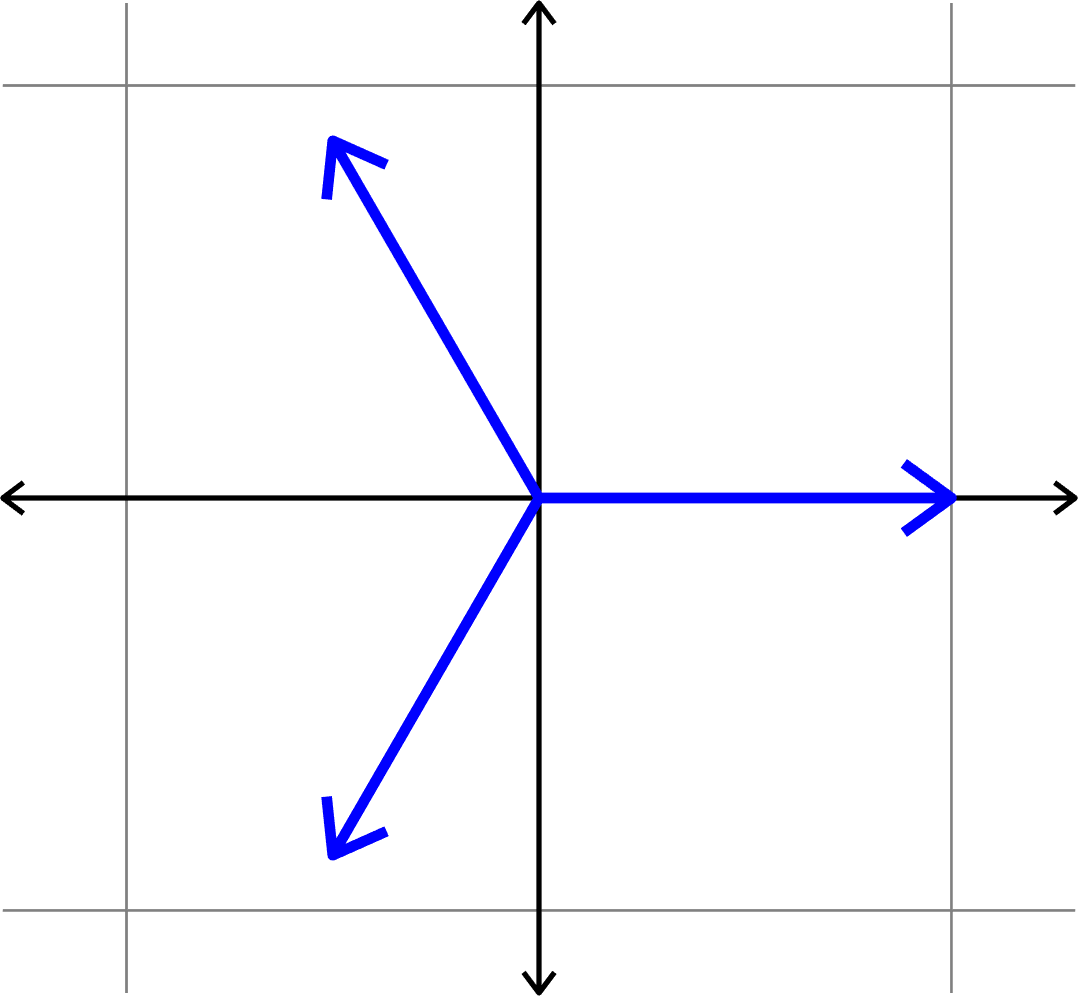
Example.
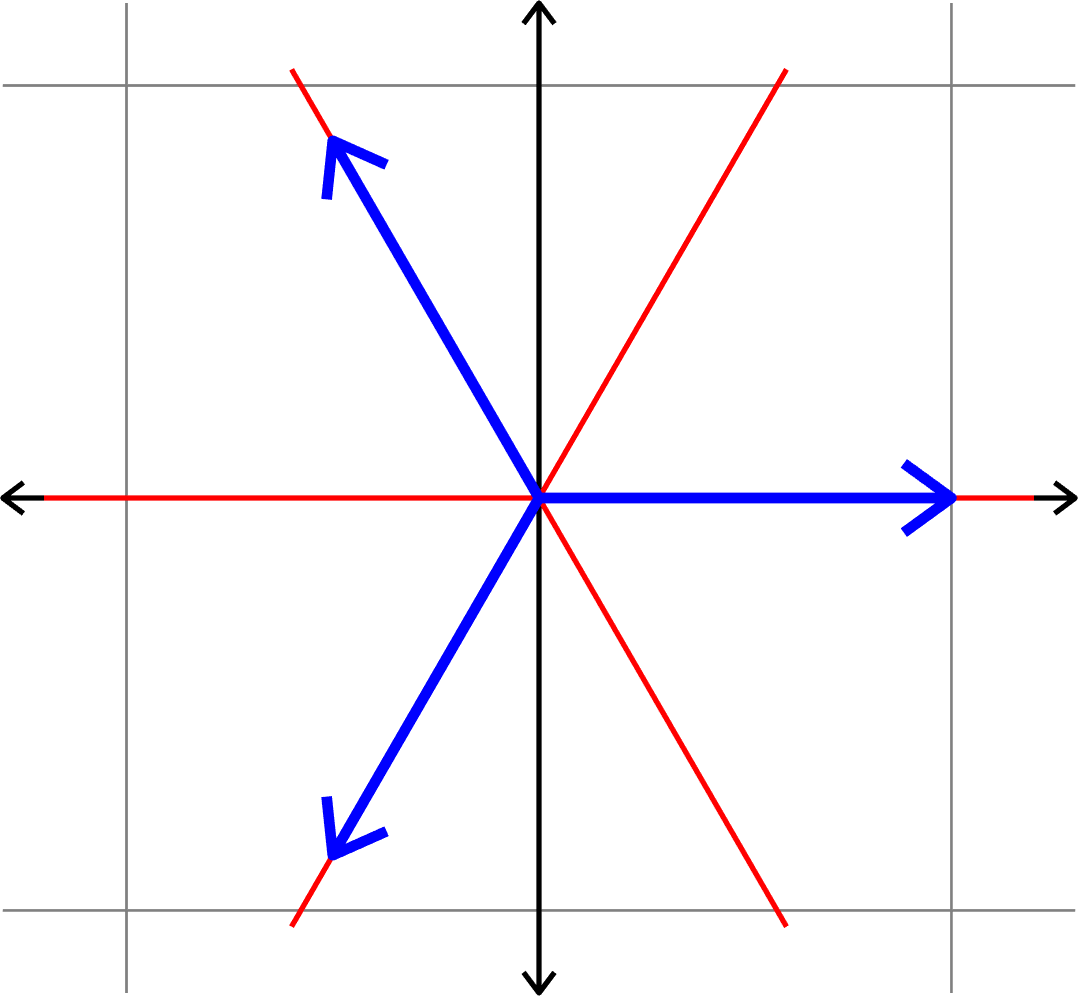
Measuring how "spread out" vectors are
Definition. Given unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\), we define the coherence
\[\mu(\Phi) = \max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|.\]
Given \((D,N)\), find \(\Phi = (\varphi_{i})_{i=1}^{N}\subset\mathbb{F}^{D}\) such that \(\mu(\Phi)\) is minimal.
Goal:
Vectors that are as spread out as possible
Theorem (the Welch bound). For unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{F}^D\)
\[\mu(\Phi)\geq \sqrt{\frac{N-D}{D(N-1)}}.\]
Equality holds if and only if both:
- Tight: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]
- Equiangular: There is a constant \(\alpha\) such that \[|\langle\varphi_{i},\varphi_{j}\rangle| = \alpha\quad\text{for all }i\neq j.\]
Welch bound equality \(\Longleftrightarrow\) equiangular tight frame (ETF)
The Short, Fat Matrix
Definition. Let \[\Phi = \big[\varphi_{1}\ \ \varphi_{2}\ \ \cdots\ \ \varphi_{N}\big]\in \mathbb{F}^{D\times N},\]
be a rank \(d\) matrix where each column \(\varphi_{n}\) has equal norm.
1) (Tightness) \(\exists\,A>0\) such that \(\Phi\Phi^{\ast} = A\mathbf{I}\).
i.e. the rows of \(\Phi\) are orthogonal & equal norm
2) (Equiangular) \(\exists\,B>0\) such that \(|\frac{1}{B}\varphi_{m}^{\ast}\varphi_{n}^{}|=1\) for \(m\neq n\).
If both 1) and 2) hold, then \((\varphi_{n})_{n=1}^{N}\) is an ETF(\(D,N)\).
(\(\mathbb{F} = \mathbb{C}\) or \(\mathbb{R}\))
Examples of equiangular tight frames
Example 2. Consider the (multiple of a) unitary matrix
Example 1. Consider the (multiple of a) unitary matrix
\[\left[\begin{array}{rrrr}1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1\\ \sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
\[\left[\begin{array}{rrrr}\sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]

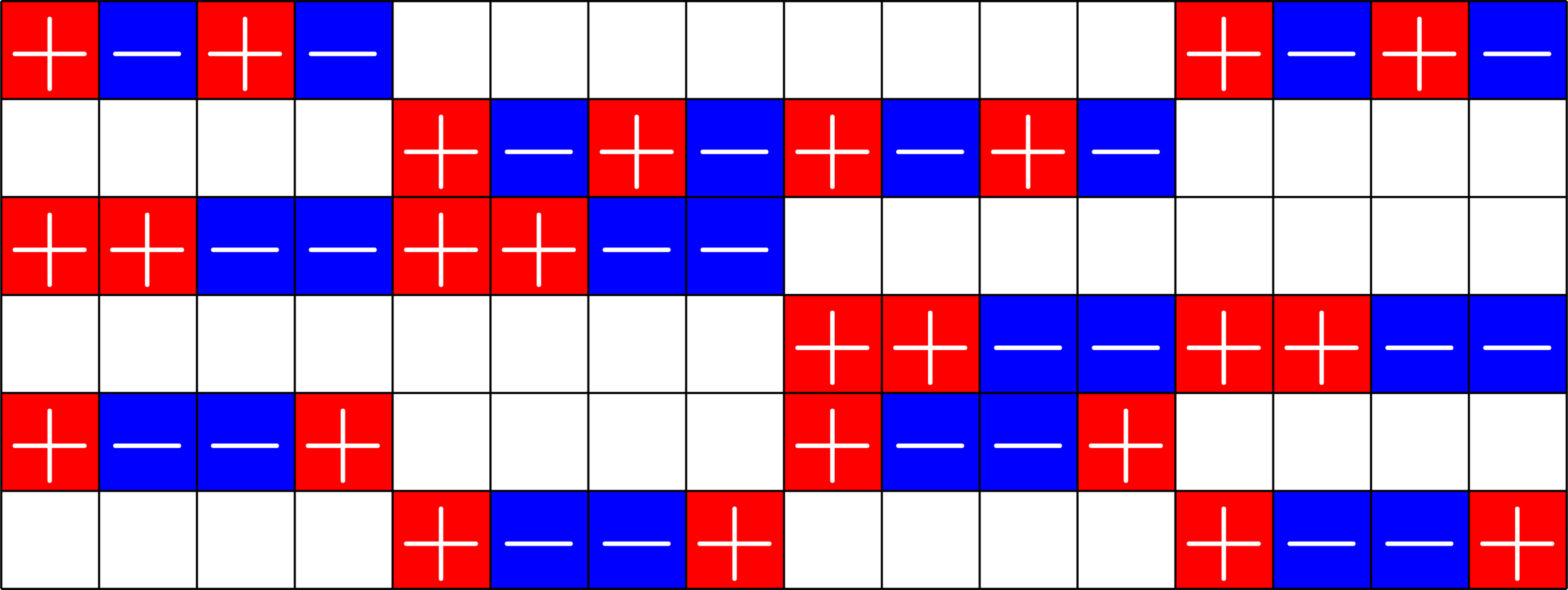
Example 3. \(\operatorname{ETF}(6,16)\)
- Rows are orthogonal
- Rows are equal norm
- all dot products of columns are \(\pm 1\)
Compatible Orthobiangular
Tight Frames
- \((\Phi_{j}^{\ast}\Phi_{j}^{})^2 = A\Phi_{j}^{\ast}\Phi_{j}^{} \) (tight, same \(A\))
- Off-diagonal \(\Phi_{j}^{\ast}\Phi_{j}^{}\) has modulus in \(\{0,1\}\) (orthobiangular)
- Off-diagonals supports \(\Phi_{j}^{\ast}\Phi_{j}^{}\) form partition (tiling)
- Compatibility condition:
Definition (Fickus, J, Myers). A sequence of matrices with \(M\) columns each
\[\Phi_{0},\Phi_{1},\ldots,\Phi_{L-1}\]
is a compatible orthobiangular tight frame (COBTF) if:
\(\Phi_{1},\Phi_{2},\ldots,\Phi_{L-1}\) are \(C\times M\) matrices.
\(\Phi_{0}\) "the special layer" is \(C_{0}\times M\) where
\[C_{0} = C \pm\frac{M}{A}\]
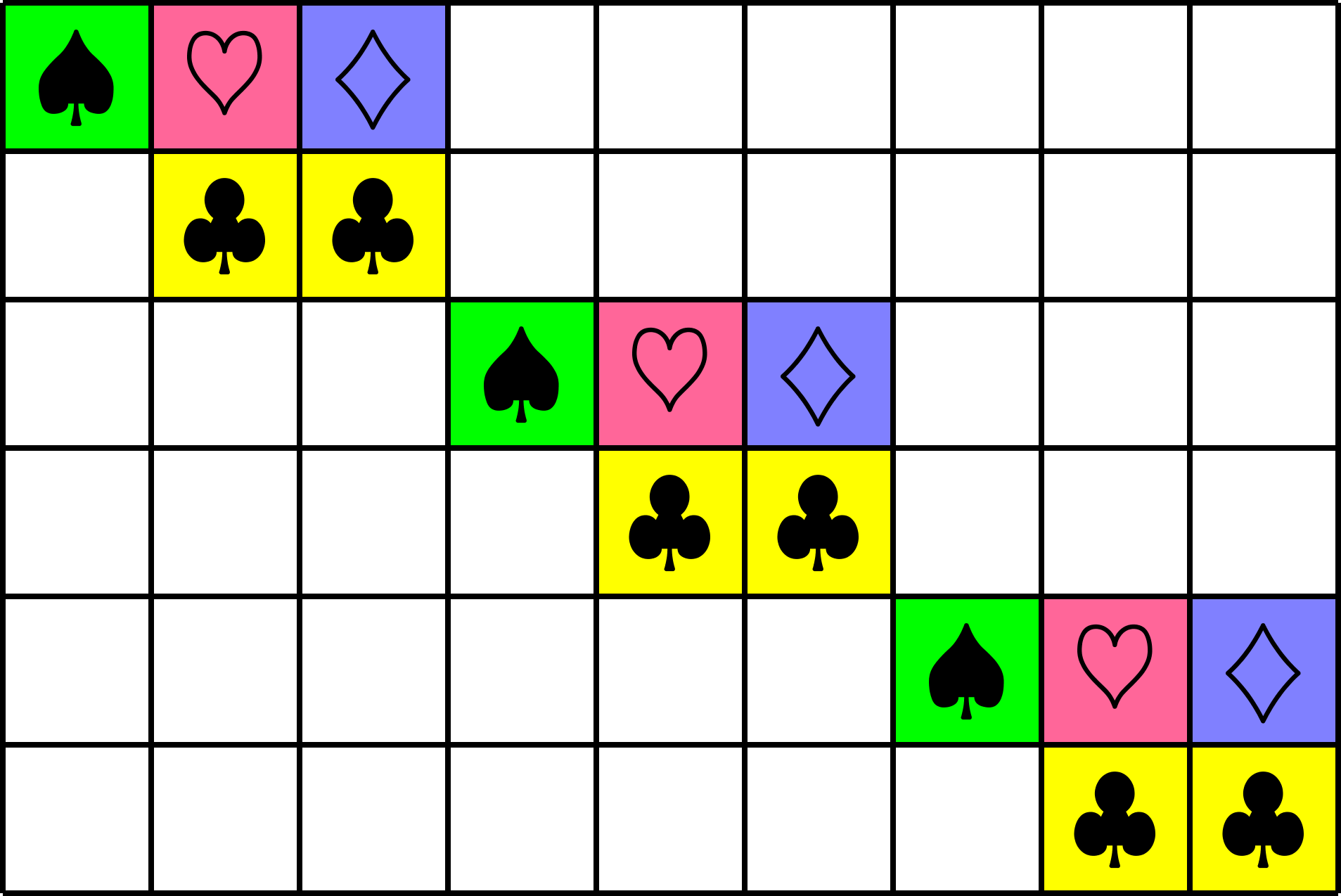
Affine plane of order \(3\)
Let \(\mathbb{F}_{3}\) be the finite field of order \(3\).
Consider the line-point incidence matrix of \(\mathbb{F}_{3}^{2}\):
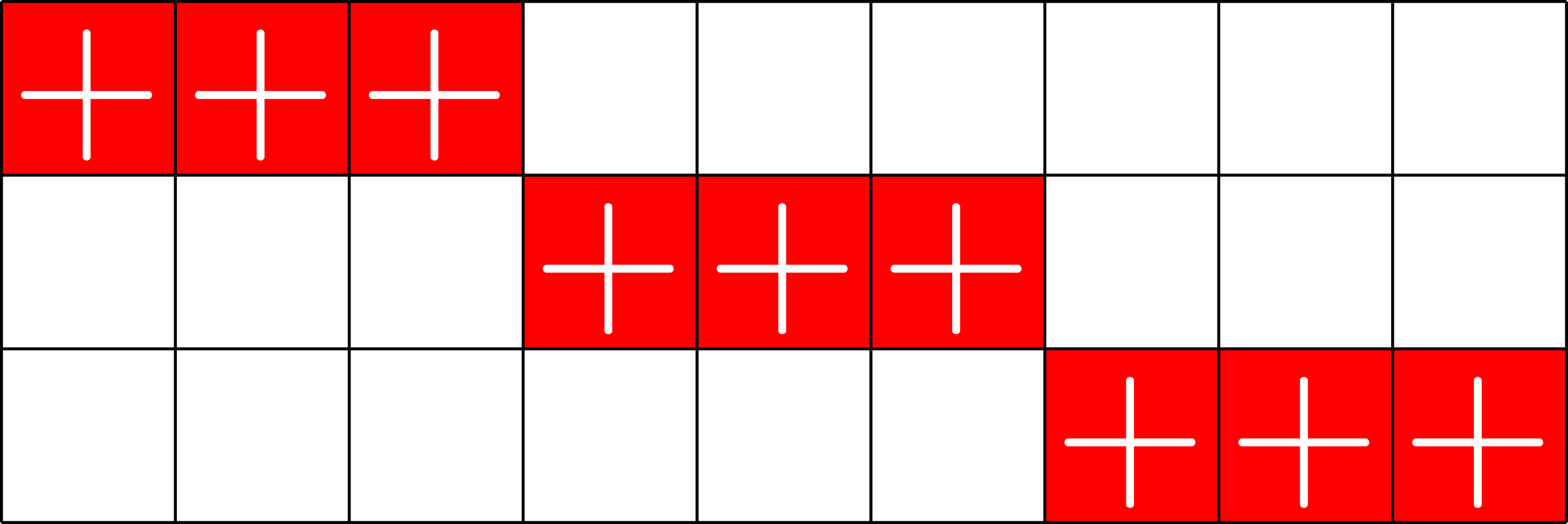



Affine plane of order \(3\)
Let \(\mathbb{F}_{3}\) be the finite field of order \(3\).
Consider the line-point incidence matrix of \(\mathbb{F}_{3}^{2}\):
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)




Partition the lines into "parallel classes"
Tight
Each \(\Phi_{j}\) is a tight frame
(w/ same frame bound \(A=3\))
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)




Rows are orthogonal
equal norm
Orthobiangular
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)




\(\Phi_{0}^{\ast}\Phi_{0} =\)
\(\Phi_{1}^{\ast}\Phi_{1} =\)
\(\Phi_{2}^{\ast}\Phi_{2} =\)
\(\Phi_{3}^{\ast}\Phi_{3} =\)




Tiling
\(\Phi_{0}^{\ast}\Phi_{0} =\)
\(\Phi_{1}^{\ast}\Phi_{1} =\)
\(\Phi_{2}^{\ast}\Phi_{2} =\)
\(\Phi_{3}^{\ast}\Phi_{3} =\)





\(\Phi_{0}^{\ast}\Phi_{0}\)
\(=\)
Tiling
\(\Phi_{0}^{\ast}\Phi_{0} =\)
\(\Phi_{1}^{\ast}\Phi_{1} =\)
\(\Phi_{2}^{\ast}\Phi_{2} =\)
\(\Phi_{3}^{\ast}\Phi_{3} =\)






\(\Phi_{0}^{\ast}\Phi_{0}\)
\(+\Phi_{1}^{\ast}\Phi_{1}\)
\(=\)
Tiling
\(\Phi_{0}^{\ast}\Phi_{0} =\)
\(\Phi_{1}^{\ast}\Phi_{1} =\)
\(\Phi_{2}^{\ast}\Phi_{2} =\)
\(\Phi_{3}^{\ast}\Phi_{3} =\)







\(\Phi_{0}^{\ast}\Phi_{0}\)
\(+\Phi_{1}^{\ast}\Phi_{1}\)
\(\ + \Phi_{2}^{\ast}\Phi_{2}\)
\(=\)
Tiling
\(\Phi_{0}^{\ast}\Phi_{0} =\)
\(\Phi_{1}^{\ast}\Phi_{1} =\)
\(\Phi_{2}^{\ast}\Phi_{2} =\)
\(\Phi_{3}^{\ast}\Phi_{3} =\)








\(\Phi_{0}^{\ast}\Phi_{0}\)
\(+\Phi_{1}^{\ast}\Phi_{1}\)
\(\ + \Phi_{2}^{\ast}\Phi_{2}\)
\(\ + \Phi_{3}^{\ast}\Phi_{3}\)
\(=\)
Melding the layers




\(\otimes \)
\(\otimes \)
\(\otimes\)
\(\otimes \)

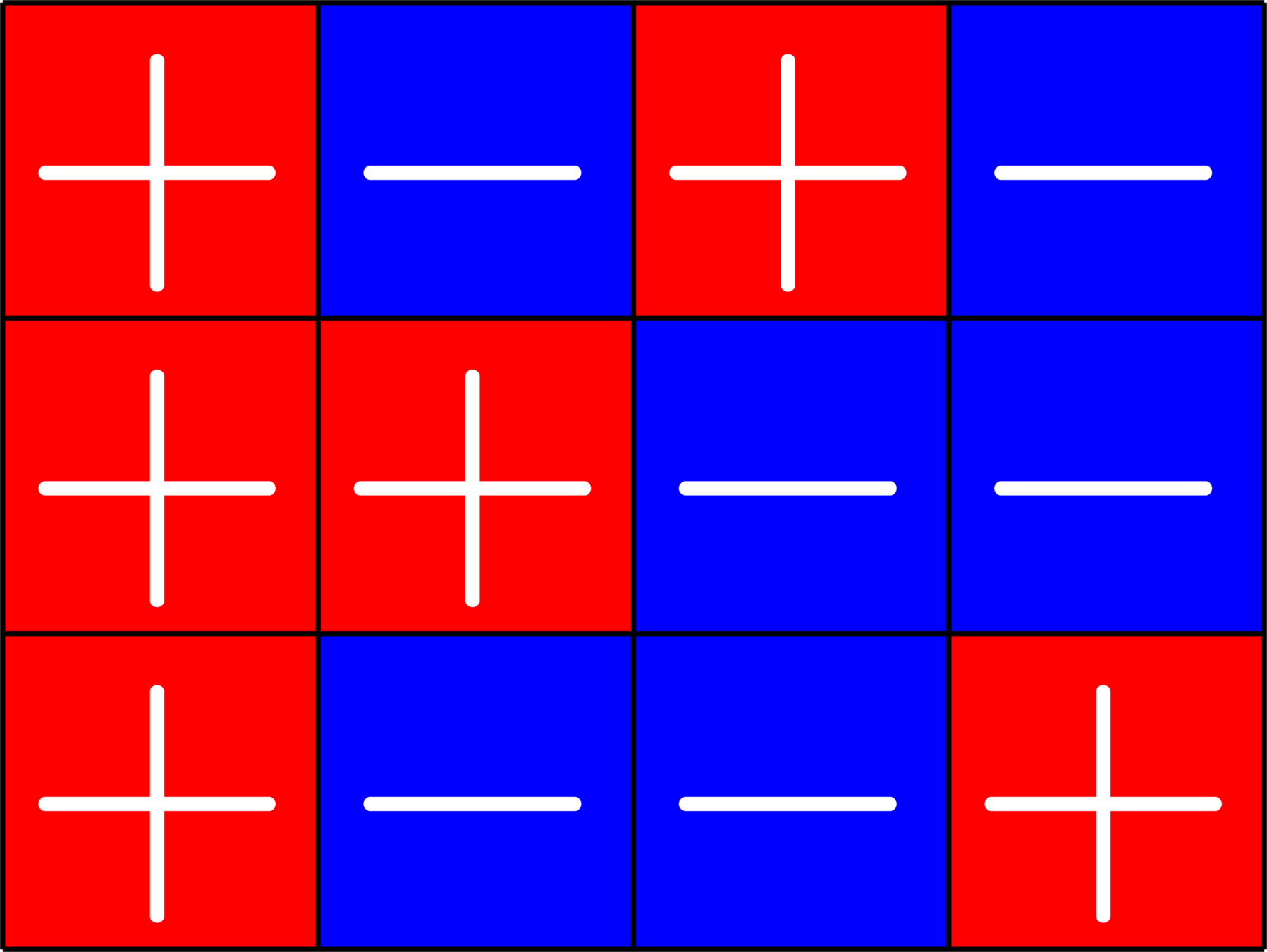


Take your favorite tight frame with 4 rows:
\(\Psi = \)
Melding the layers
It's always a tight frame!
\(\Psi = \)
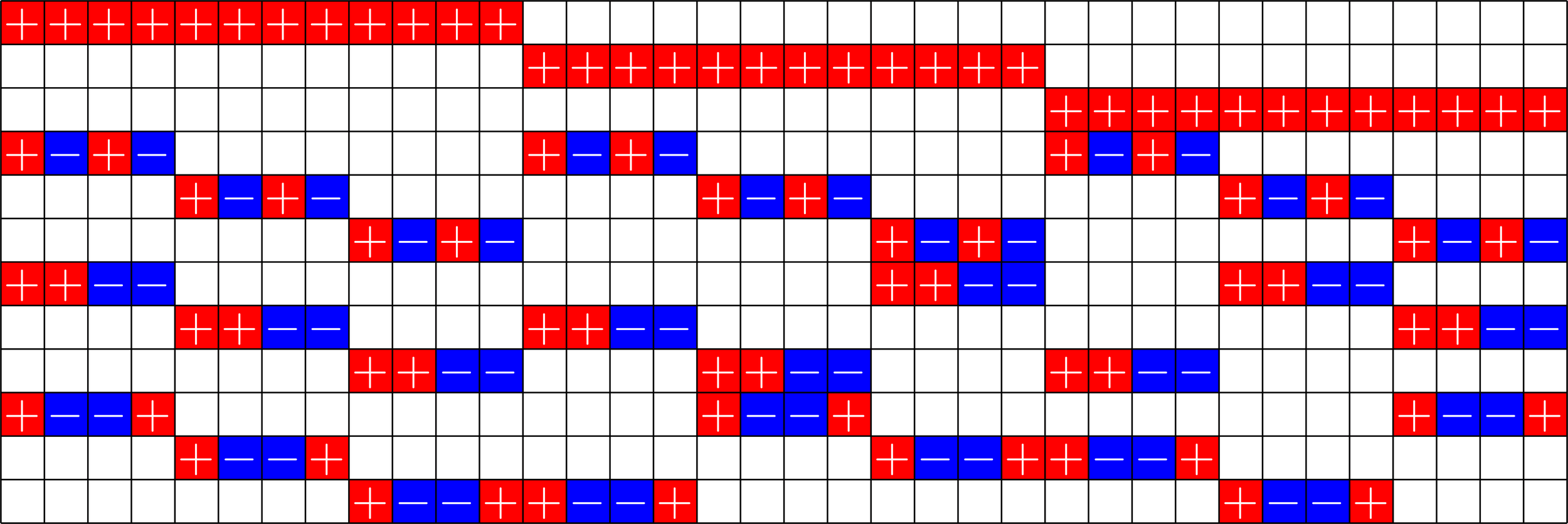
Melding the layers
It's always a tight frame!
\(\Psi^{\ast}\Psi = \)
It's not an ETF :(
Still a nice frame!
For 36 vectors in \(\mathbb{R}^{12}\), this frame has the best known coherence!
One more condition: Compatibility
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)




There's another nice set of matrices that are tight, orthobiangular, and tile
Take the Naimark complement
One more condition: Compatibility
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)



There's another nice set of matrices that are tight, orthobiangular, and tile






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
One more condition: Compatibility
Now, the "Compatibility condition" holds:
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)




\(\Phi_{1},\Phi_{2},\ldots,\Phi_{L-1}\) are \(C\times M\) matrices.
\(\Phi_{0}\) "the special layer" is \(C_{0}\times M\) where
\[C_{0} = C \pm\frac{M}{A}\]
Let's try that "melding" again




\(\otimes \)
\(\otimes \)
\(\otimes\)
\(\otimes \)




\(\Psi = \)
Did we fix it?
\(\Psi = \)
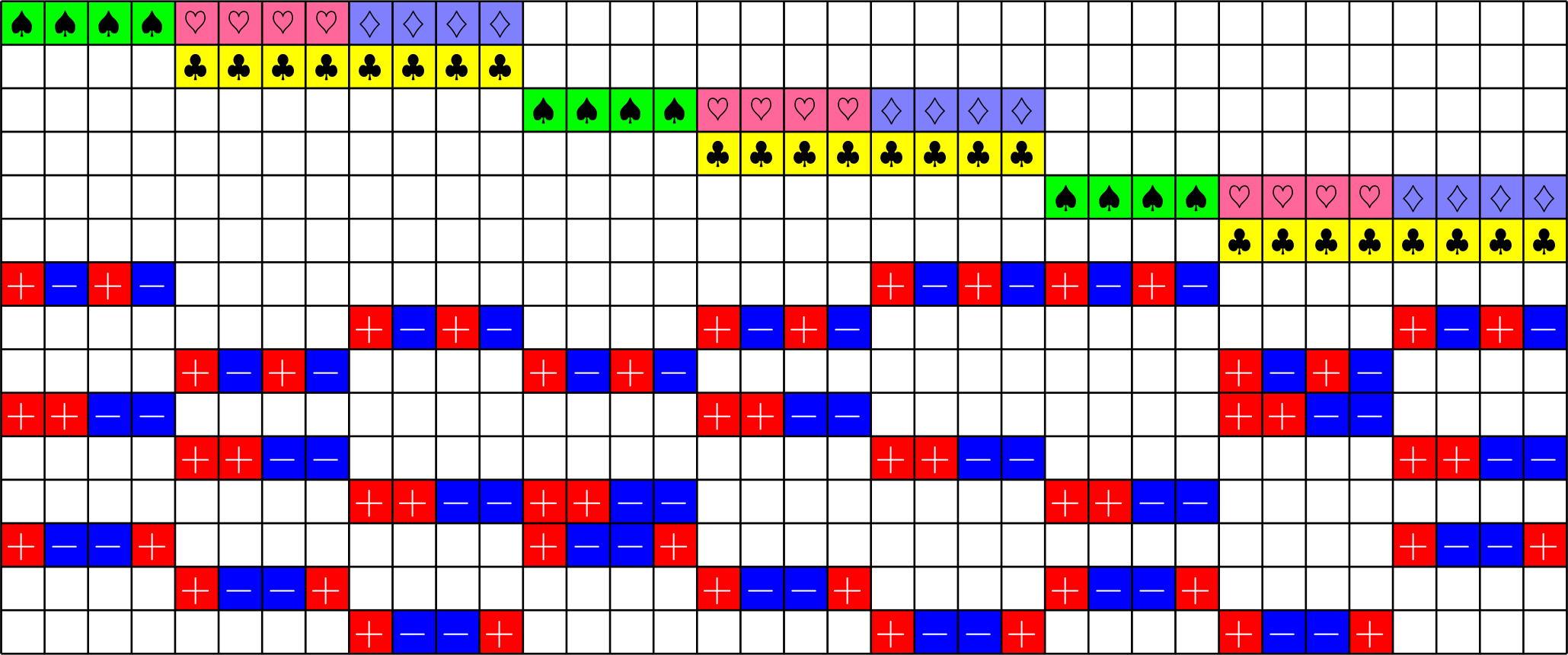
Did we fix it? YES!
\(\Psi^{\ast}\Psi = \)
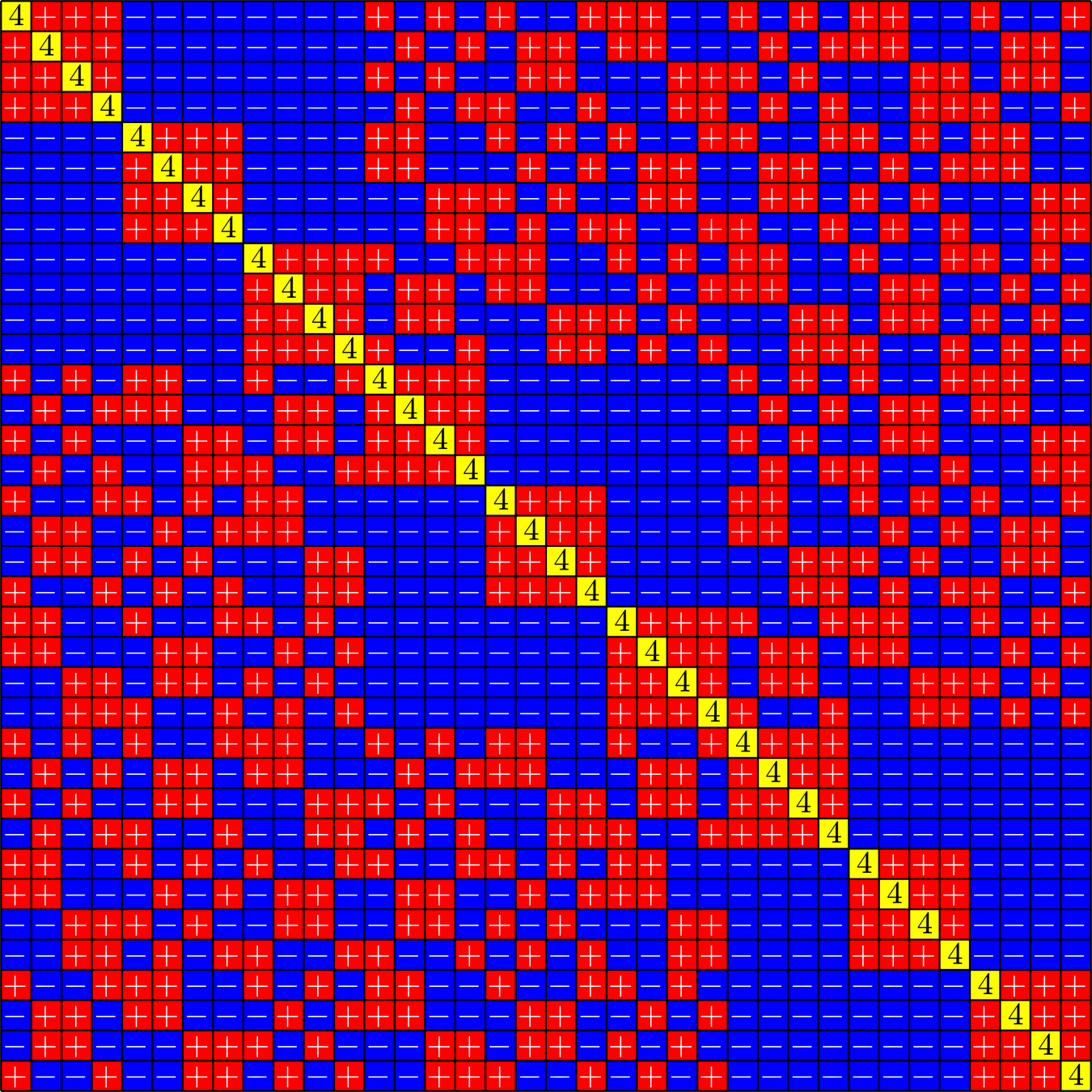
Theorem (Fickus, J, Myers '25). A sequence of matrices with \(M\) columns each
\[\Phi_{0},\Phi_{1},\ldots,\Phi_{L-1}\]
is a compatible orthobiangular tight frame (COBTF) if:
- \((\Phi_{j}^{\ast}\Phi_{j}^{})^2 = A\Phi_{j}^{\ast}\Phi_{j}^{} \) (\(\text{tight, same }A)\)
- Off-diagonal \(\Phi_{j}^{\ast}\Phi_{j}^{}\) has modulus in \(\{0,1\}\) (orthobiangular)
- Off-diagonals supports \(\Phi_{j}^{\ast}\Phi_{j}^{}\) partition (tiling)
- "Compatibility condition"
If \((h_{i})_{i=0}^{L-1}\) are the rows of a (possibly complex) Hadamard matrix, then
\[\Psi = \begin{bmatrix}\Phi_{0}\otimes h_{0}\\ \Phi_{1}\otimes h_{1}\\ \vdots\\ \Phi_{L-1}\otimes h_{L-1}\end{bmatrix}\]
is an ETF.
How do we find COBTFs?
- Balanced incomplete block designs
- Group divisible designs
- Harmonically?
\[\Z_{7}\left\{\begin{array}{c} 0\\ 1\\ 2\\ 3\\ 4\\ 5\\ 6 \end{array}\right. \left[\begin{array}{ccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^3 & \omega^6 & \omega^2 & \omega^5 & \omega & \omega^4\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3\\ 1 & \omega^5 & \omega^3 & \omega & \omega^6 & \omega^4 & \omega^2\\ 1 & \omega^6 & \omega^5 & \omega^4 & \omega^3 & \omega^2 & \omega \end{array}\right]\]
\[\begin{array}{c} 1\\ 2\\ 4 \end{array}\left[\begin{array}{ccccccc} 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3 \end{array}\right]\]
(\(\omega = e^{2\pi i/7}\))
Harmonic Frames, aka rows from a DFT
\[\Phi = \left[\begin{array}{ccccccc} 1 & \omega & \omega^2 & \omega^3 & \omega^4 & \omega^5 & \omega^6\\ 1 & \omega^2 & \omega^4 & \omega^6 & \omega & \omega^3 & \omega^5\\ 1 & \omega^4 & \omega & \omega^5 & \omega^2 & \omega^6 & \omega^3 \end{array}\right]\]
Harmonic Frames, aka rows from a DFT
\(\Phi\) is tight, since it is rows out of a unitary.
\(\Phi\) is equiangular, since \(D=\{1,2,4\}\subset\Z_{7}\) is a difference set.
That is, if we look at the difference table
\[\begin{array}{r|rrr} - & 1 & 2 & 4\\ \hline 1 & 0 & 6 & 4\\ 2 & 1 & 0 & 5\\ 4 & 3 & 2 & 0 \end{array}\]
every nonidentity group element shows up the same number of times
Can we find sets \(D_{0},D_{1},\ldots,D_{L-1}\subset G\) such that the corresponding harmonic frames form a COBTF?
Quartets
Definition.
- \(G\) - finite abelian group of order \(r^2\)
- \(D_{0},D_{1},D_{2},D_{3}\subseteq G\) of size \(\dfrac{r^2-r}{2}\)
- \(\{D_{i}\}_{i=0}^{4}\) is a quartet if for each nontrivial character \(\chi\) \[\chi(D_{i})=\sum_{g\in D_{i}}\chi(g)\] is nonzero for exactly one \(i\) where it's value is \(\pm r\).
Theorem (Fickus, J, Myers '25). If \(\{D_{i}\}_{i=0}^{3}\) is a quartet in \(G\), then the harmonic frames associated with \(G\setminus D_{0}, D_{1},D_{2},D_{3}\) for a COBTF.
Example. In \(G = \Z_{3}\times\Z_{3}\) we have the quartet:
\(D_{0} = \{(0,0),(1,2),(2,1)\}\)
\(D_{1} = \{(0,0),(2,0),(1,0)\}\)
\(D_{2} = \{(0,0),(1,1),(2,2)\}\)
\(D_{3} = \{(0,0),(0,2),(0,1)\}\)



Pull these rows out of the DFT:




\((0,0)\)
\((1,0)\)
\((2,0)\)



\(=1\) \(=e^{2\pi i/3}\) \(=e^{4\pi i/3}\)
\(\Phi_{0} = \)
\(\Phi_{1} = \)
\(\Phi_{2} = \)
\(\Phi_{3} = \)
\(\Phi_{0}^{\ast}\Phi_{0} = \frac{1}{3}\)




\(\Phi_{1}^{\ast}\Phi_{1} = \frac{1}{3}\)
\(\Phi_{2}^{\ast}\Phi_{2} = \frac{1}{3}\)
\(\Phi_{3}^{\ast}\Phi_{3} = \frac{1}{3}\)











\(+\)
\(+\)
\(+\)
\(=\)

Theorem.
- Let \(r=3^j m^2\) for \(j\geq 0\) and \(2,3\nmid m\).
- \(\exists\) quartet in a group of order \(r^2\).
Quartets are abundant
Corollary.
- Let \(r=3^j m^2\) for \(j\geq 0\) and \(2,3\nmid m\)
- \(\exists\,\) real ETF with \(4r^2\) vectors in \(\R^{2r^2-r}\).
Theorem (Fickus, J, Myers '25). Given a quartet in a group of order \(r^2\) and a resolvable \(\operatorname{BIBD}(V,r^2,1)\) there exists a COBTF with \(\frac{4(V-1)}{r^2-1}\) layers.
Chen's Pullback Trick
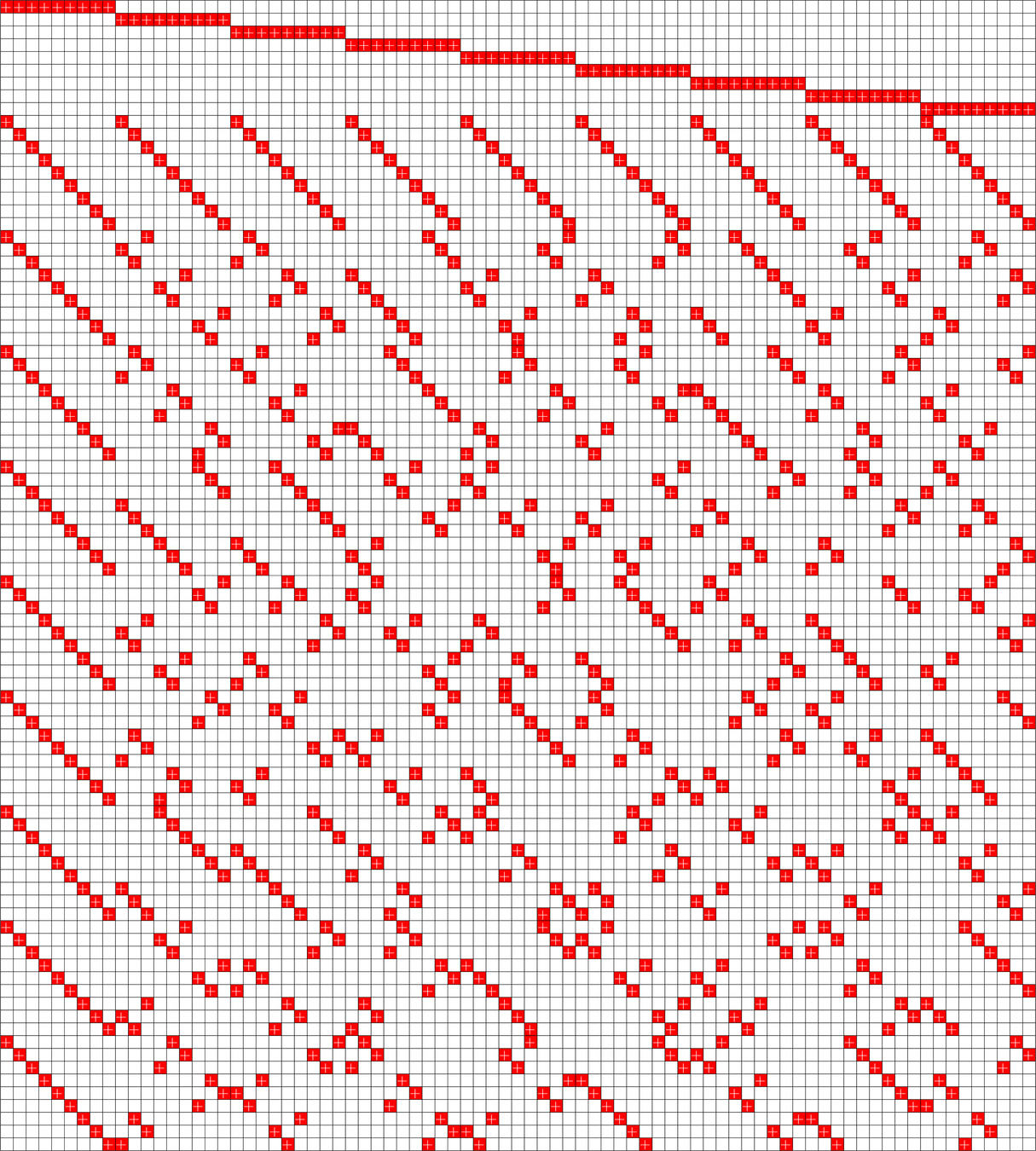





\(\operatorname{BIBD}(81,9,1)\)
Quartet in \(\Z_{3}^2\)
Theorem (Fickus, J, Myers '25). Given a quartet in a group of order \(r^2\) and a resolvable \(\operatorname{BIBD}(V,r^2,1)\) there exists a COBTF with \(\frac{4(V-1)}{r^2-1}\) layers.
Chen's Pullback Trick


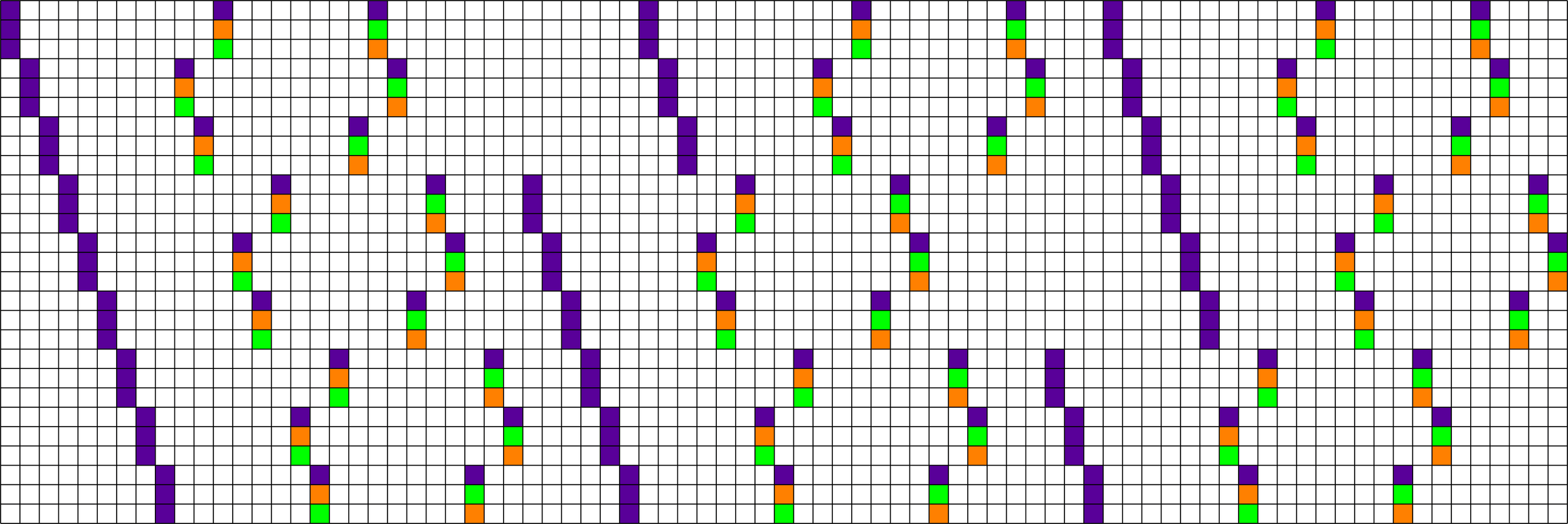
"\(\otimes\)"
Replace each \(+1\) with a column
Theorem (Fickus, J, Myers '25). Given a quartet in a group of order \(r^2\) and a resolvable \(\operatorname{BIBD}(V,r^2,1)\) there exists a COBTF with \(\frac{4(V-1)}{r^2-1}\) layers.
Chen's Pullback Trick: New ETFs
Theorem (Fickus, J, Myers '25). Given a quartet in a group of order \(r^2\) and a resolvable \(\operatorname{BIBD}(V,r^2,1)\) ETF with \(N\) vectors in \(\mathbb{C}^{D}\) where
\[N=\frac{4V(V-1)}{r^2-1}\quad\text{and}\quad D = \frac{V(2V+r-1)}{r(r+1)}.\]
Moreover, if there exists a real Hadamard matrix of order \(\frac{4(V-1)}{r^2-1}\), then the ETF can be made real and either centered or axial.
Example.
- Quartet in \(\Z_{5}^{4}\)
- Affine plane over \(\mathbb{F}_{5^4}\) \(\leadsto\) resolvable \(\operatorname{BIBD}(390625, 625, 1)\)
- \(\exists\) real Hadamard order 2504
- New real ETF 978,125,000 in 469,515,625 dimensions!!!
An open question
Is there a COBTF w/ four layers
- \(\Phi_{0}\) is a \(6\times 72\) real orthobiangular tight frame,
- \(\Phi_{1},\Phi_{2},\Phi_{3}\) are \(12\times 72\) real OBTFs?
Then you'll have an \(\operatorname{ETF}(42,288)\).

Thanks!
- This work was partially supported by NSF #1830066
- Webpage: https://tinyurl.com/jasperAFIT
- Slides: https://slides.com/johnjasper
