Computing order zeta functions via resolution of singularities

Joshua Maglione

Universität Bielefeld

www.slides.com/joshmaglione/bva2019

jmaglione@math.uni-bielefeld.de

Creative Commons Attribution 4.0 International License

Reporting on work in progress with ...

Christopher Voll

Bernd Schober

Anne Frühbis-Krüger

Universität Bielefeld

Universität Oldenburg

Enumerating subgroups of \(\mathbb{Z}^d\)

For \(d=1\), exactly one subgroup of index \(n\), for all \(n \geq 1\).

Record this in a Dirichlet generating function:

\displaystyle\zeta_{\mathbb{Z}}^{<}(s) = \sum_{H\leq_f \mathbb{Z}} |\mathbb{Z} : H|^{-s} = \sum_{n\geq 1} a_n(\mathbb{Z})n^{-s} = \sum_{n\geq 1} n^{-s}.

For the general case, it is slightly more complicated.

\displaystyle\zeta_{\mathbb{Z^d}}^{<}(s) = \zeta(s) \zeta(s - 1) \cdots \zeta(s - d + 1).

Challenging to explicitly compute for general groups, but \(\mathbb{Z}^d\) is easy.

What about subrings of \(\mathbb{Z}^d\)?

All our subrings are unital. Nontrivial examples occur when \(d \geq 3\).

The \(d = 3\) case follows from Datskovsky–Wright (1986).

Subring zeta function satisfies an Euler product decomposition:

\displaystyle\zeta_{\mathbb{Z}^d}(s) = \prod_{p \text{ prime}} \zeta_{\mathbb{Z}^d,p}(s) = \prod_{p \text{ prime}} \zeta_{\mathbb{Z}_p^d}(s).

\displaystyle\zeta_{\mathbb{Z}_p^3}(s) = \dfrac{1 + 2p^{-s} + p^{-2s}}{(1 - p^{-s}) (1 - p^{1 - 3s})}.

The zeta functions \(\zeta_{R, p}(s)\) are called local zeta functions.

Nakagawa (1996) and Liu (2007) prove that \(\zeta_{\mathbb{Z}_p^4}(s)\) is

\dfrac{ 1 + 4p^{-s} + 2p^{-2s} + (4p - 3)p^{-3s} + \cdots + (3p^2 - 4p)p^{-6s} - 2p^{2-7s} - 4p^{2-8s} - p^{2-9s} }{ (1 - p^{-s})^2 (1 - p^{2-4s}) (1 - p^{3-6s})}

The \(d \geq 5\) case is open.

Notice some properties of the local subring zeta functions:

Rational function in both \(p\) and \(p^{-s}\)

\(\Longrightarrow\) exists recurrence relation among \(a_n(\mathbb{Z}^d)\)

Palindromic numerators

\(\Longrightarrow\) suggests restrictive geometric structure

Uniform for all primes \(p\)

\(\Longrightarrow\) suggests nice structure of underlying varieties

\begin{aligned} \zeta_{\mathbb{Z}_p^3}(s) = \dfrac{1 + 2p^{-s} + p^{-2s}}{(1 - p^{-s}) (1 - p^{1 - 3s})} \end{aligned}

The general setting

Fix a number field \(K\) and its ring of integers \(\mathcal{O}_K\).

The order zeta function is

\displaystyle\zeta_K(s) = \sum_{1\in H\leq \mathcal{O}_K} |\mathcal{O}_K : H|^{-s} = \sum_{n\geq 1} a_n(\mathcal{O}_K) n^{-s},

where \(H\) runs over all finite index subrings of \(\mathcal{O}_K\), i.e. suborders.

These order zeta functions give analytic data of a fixed order, \(\mathcal{O}_K\).

Different perspectives consider all sub-orders with other properties.

See Kaplan et al. (2015), Brakenhoff (2009), Bhargava (2005).

Order zeta functions have an Euler product decomposition:

\displaystyle\zeta_K(s) = \prod_{p\text{ prime}} \zeta_{K, p}(s) = \prod_{p \text{ prime}} \zeta_{K\otimes\mathbb{Z}_p}(s),

where the product runs over all rational primes \(p\) in \(K\).

There are subtleties based on how \(p\) splits in \(K\). We consider the totally split case, so that

\zeta_{K, p}(s) = \zeta_{\mathbb{Z}_p^d}(s)

The ring \(\mathbb{Z}^d\) has one key advantage:

R \cong 1\!\cdot\!\mathbb{Z} \oplus R'.

Instead, count multiplicatively closed sublattices of \(R'\):

\begin{aligned} \zeta_{\mathbb{Z}_p^d}(s) &= \zeta_{\mathbb{Z}_p^{d-1}}^{<}(s) \end{aligned}

That is, enumerate not necessarily unital subrings of \(R'\).

\(p\)-adic cone integrals

We represent \(\zeta_{K,p}^<(s)\) as a \(p\)-adic cone integral. Notation:

For integers \(\ell,m\), a sequence of polynomials in \(\mathbb{Z}[x_1,\dots, x_m]\),

\mathscr{D} = \left(f_0, g_0;\, f_1, g_1,\, \dots,\, f_\ell, g_\ell \right)

is called cone integral data.

Associate to \(\mathscr{D}\), the closed subset of \(\mathbb{Z}_p^m\):

\mathscr{M}(\mathscr{D}, p) = \left\{x \in \mathbb{Z}_p^m ~\middle|~ \nu_p(f_i(x)) \leq \nu_p(g_i(x)), \; i\geq 1\right\}

and the following cone integral:

Z_{\mathscr{D}}(s, p) = \displaystyle\int_{\mathscr{M}(\mathscr{D}, p)} \left|f_0(x)\right|_p^s \left|g_0(x)\right|_p \,d\mu(x).

\nu_p : p\text{-adic valuation},\qquad |\cdot |_p : p\text{-adic norm}, \\ \mu : \text{normalized Haar measure so }\mu(\mathbb{Z}_p^m) = 1.

The order zeta functions are equal to suitable cone integrals.

\displaystyle\zeta_{K, p}(s) = \int_{\mathscr{M}(\mathscr{D}, p)} |f_0(x)|_p^s |g_0(x)|_p \, d\mu(x).

Ex: A cone integral for the subring zeta function of \(\mathbb{Z}_p^3\) is

where the set \(\mathscr{M}\) contains all \(x\in\mathbb{Z}_p^3\) satisfying

\begin{aligned} \nu_p(x_{11}) &\leq \nu_p(x_{21}(x_{21} - x_{22})) .%, \\ %\nu_p(x_{11}) &\leq \nu_p(x_{21}(x_{31}-x_{32})), \\ %\nu_p(x_{22}) &\leq \nu_p(x_{32}(x_{32} - x_{33})), \\ %\nu_p(x_{11}x_{22}) &\leq \nu_p(x_{22}x_{31}(x_{31} - x_{33}) - x_{21}x_{32}(x_{32} - x_{33})) . \end{aligned}

Because the cone data is not (locally) monomial, computing this requires different tools.

\displaystyle \zeta_{\mathbb{Z}_p^3}(s+2) = (1 - p^{-1})^{-2} \int_{\mathscr{M}} |x_{11}x_{22}|_p^{s} |x_{22}|_p \, d\mu(x)

Computing cone integrals via resolution of singularities

Theorem. (du Sautoy, Grunewald 2000)

Let \(L\) be a ring. There are smooth algebraic varieties \(V_t\), \(t\in\{1,\dots, m\}\), defined over \(\mathbb{Q}\), and rational functions \(W_t(X, Y)\in \mathbb{Q}(X, Y)\), such that for almost all primes \(p\),

\displaystyle\zeta_{L, p}^<(s) = \sum_{t=1}^m c_t(p) W_t(p, p^{-s}),

where \(c_t(p)\) denotes the number of \(\mathbb{F}_p\)-rational points of \(\overline{V}_t\), the reduction of \(V_t\) modulo \(p\).

From cone data \(\mathscr{D} = (f_0, g_0;\, \dots,\, f_\ell, g_\ell)\), we apply resolution of singularities to monomialize every \(f_i\) and \(g_i\).

Want an explicit resolution of the ideal generated by

\displaystyle F_d(x) = \prod_{i=0}^\ell f_i(x)g_i(x).

Challenges:

Number of variables for \(\mathbb{Z}_p^d\) case is \(\binom{d}{2}\).

Little to no useful features of \(F_d(x)\) in general.

\begin{aligned} F_3(x) &= (x_{21} - x_{22})x_{11}x_{21}x_{22} \\ F_4(x) &= (x_{22}x_{31}^2 - x_{21}x_{32}^2 + x_{21}x_{32}x_{33} - x_{22}x_{31}x_{33}) \\ &\quad \times (x_{32} - x_{33})(x_{31} - x_{32})x_{31}x_{32}x_{33}F_3(x) \end{aligned}

A (sideways) tree of blowing up:

not locally monomial

locally monomial

Du Sautoy–Grunewald give blueprint to compute cone integrals by:

(1) applying a resolution of singularities and

(2) counting \(\mathbb{F}_p\)-rational points on varieties.

Apply ideas of Bierstone–Milman (2006) and Blanco (2012a, 2012b) to monomialize binomials.

We need only monomialize \(\mathscr{D}\). Gives a little more freedom.

Solving monomial integrals

Once \(\mathscr{D}\) is monomial, translate \(p\)-adic integral to counting integral points on rational polyhedron \(\mathcal{P}\subseteq \mathbb{R}^r\).

Theorem. (Barvinok (1994))

There exists an algorithm that, given a rational polyhedron \(\mathcal{P}\) of a fixed dimension \(r\in\mathbb{N}\), returns the generating function in poly-time

Barvinok's algorithm has implementations in Sage via LattE.

We use Rossmann's Zeta package to compute monomial integrals, which also employs LattE, Rossmann (2018).

\displaystyle F_{\mathcal{P}}(X) = \sum_{\alpha\in \mathcal{P}\cap \mathbb{Z}^r} X^\alpha.

Tree of blowing ups for \(\mathbb{Z}^4\)

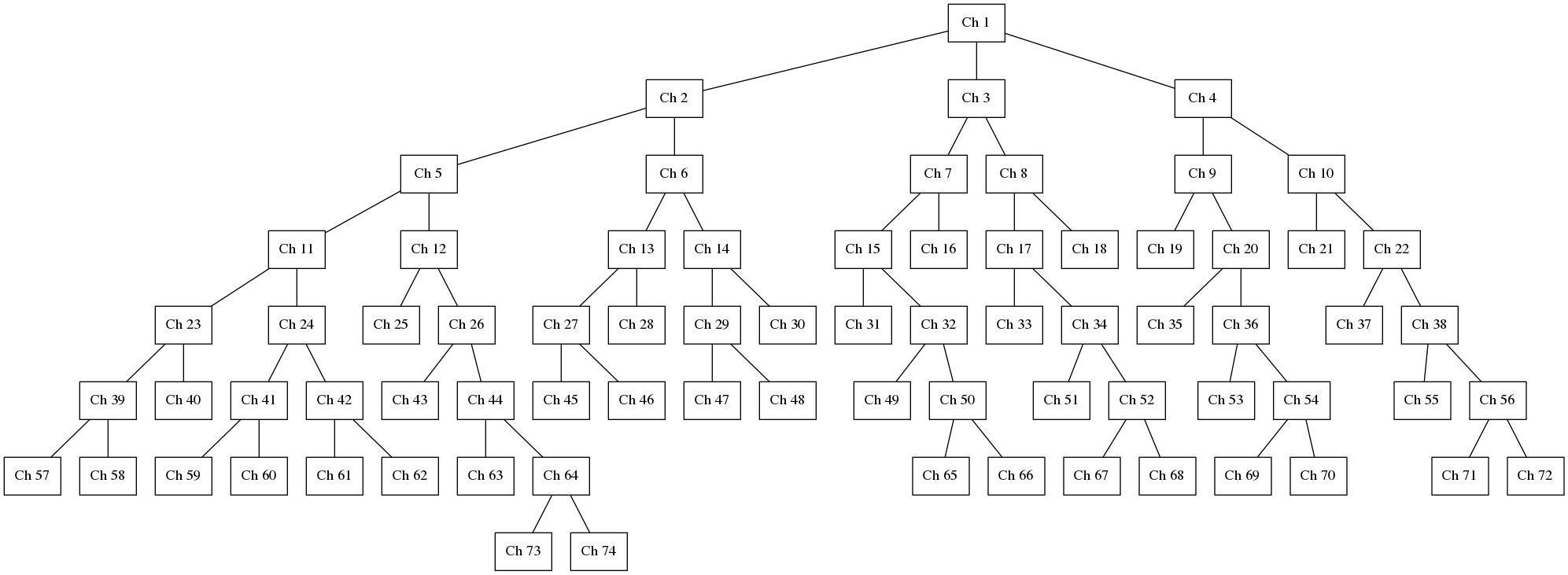
We have 74 charts, with 38 leaves and 185 monomial integrals.

We have verified \(\zeta_{\mathbb{Z}_p^4}(s)\) with our methods.

From the du Sautoy, Grunewald theorem before,

\displaystyle \zeta_{K, p}(s) = \sum_{t=1}^m c_t(p) W_t(p, p^{-s}),

where the \(c_t(p)\) enumerated the \(\mathbb{F}_p\)-rational points of \(\overline{V}_t\).

The Nakagawa, Liu formula for \(\zeta_{\mathbb{Z}_p^4}(s)\) holds for all primes \(p\).

The varieties \(V_t\) in our computation had "tame" structure.

For exactly 2 varieties, \(c_t(p)\) depended on parity of \(p\).

Of the 185 varieties, computed \(c_t(p)\) by hand for 13 of them.

For every variety, \(c_t(p)\) is given as a polynomial in \(p\) or 2 polynomials depending on if \(p = 2\) or not.

An overview of the algorithm:

(1) Locally monomialize the cone data \(\mathscr{D}\),

(2) Monomialize by counting \(\mathbb{F}_p\)-rational points on varieties,

(3) Apply Barvinok's algorithm to evaluate monomial \(p\)-adic integrals.

Still in a prototypical stage and shows promise:

for extending computations of \(\zeta_{\mathbb{Z}^d}(s)\) and to other rings like \(\mathbb{Z}[x]/(x^d)\),

for bringing computational tools from algebraic geometry to solve \(p\)-adic integrals.