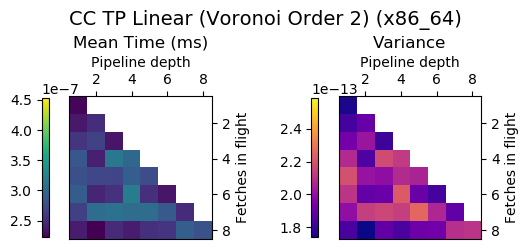Fast Spline Evaluation

Part 2: Code generation

J. Horacsek

November 20th, 2020

Where we've been...

  • Box splines (Voronoi splines too)
  • Approximation spaces
  • Optimization (within spline spaces)

Motivation

For scalar vis, we often care about evaluating functions of the form

f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)

And we want to do this quickly (on the GPU, too); this is required for interactive visualization  

Sampling Lattices

Cartesian Lattice

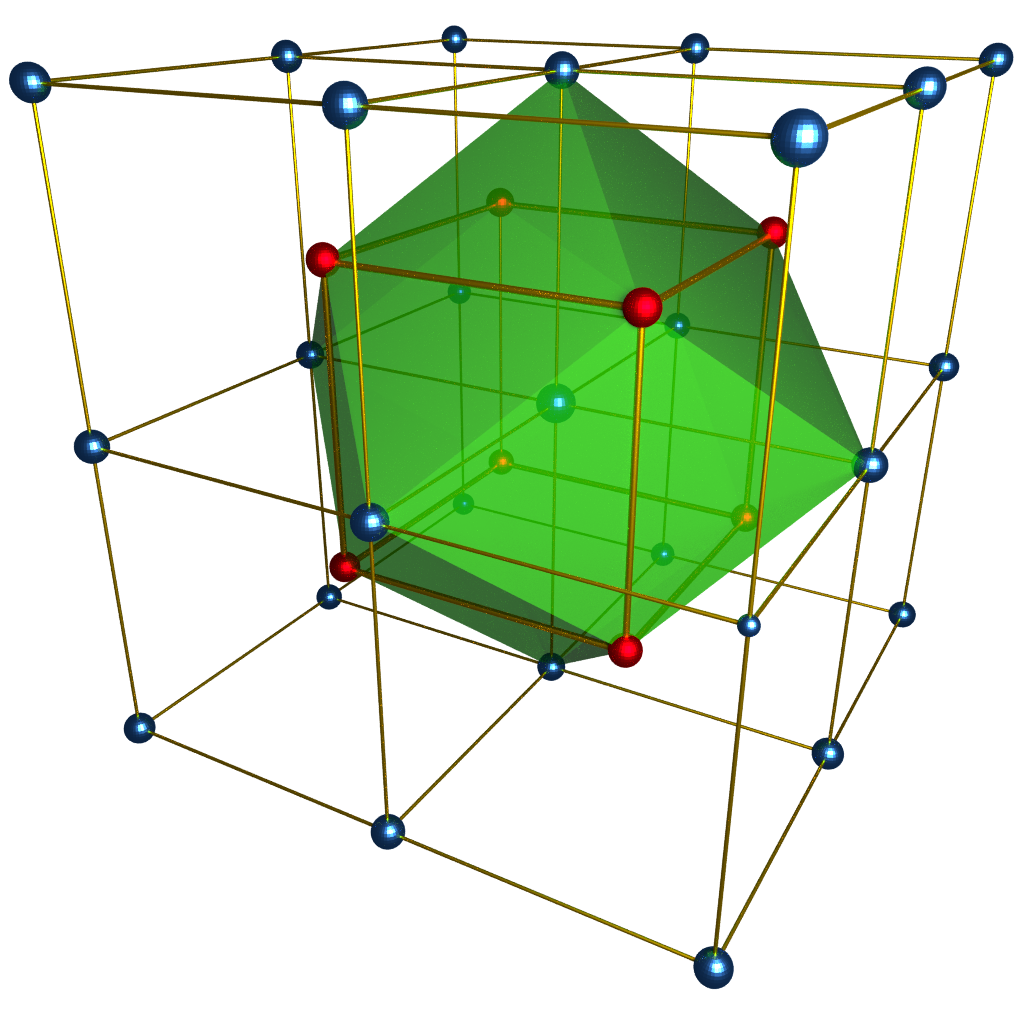
Body Centered Cubic Lattice

\displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)

L controls the point distribution

Going fast (on the GPU)

Application dictates speed, but we can make some observations to speed up computations

  • No branches in code (or at least reduce branches)
  • Minimize expensive memory fetches (by organizing fetches and using trilinear fetches)
  • Waste computation if necessary (the process is already bandwidth limited, it's ok to waste computation)

What about on the CPU?

Box Splines

Multivariate extension to B-splines

  • Compact
  • Smooth
  • Piecewise polynomials
\Xi = \begin{bmatrix} | & | & \ & | \\ \xi_1 & \xi_2 & ... & \xi_n \\ | & | & \ & | \end{bmatrix}

Start with a direction matrix

\xi_i \in \mathbb{R}^s

Box Splines

Convolutional, recursive definition

M_\Xi(x) = \displaystyle\int_0^1M_{\Xi\backslash\xi}(x - t\xi) dt \text{ \ with \ } M_{[ \ ]}(x) := \delta(x)

In one dimension, this looks like

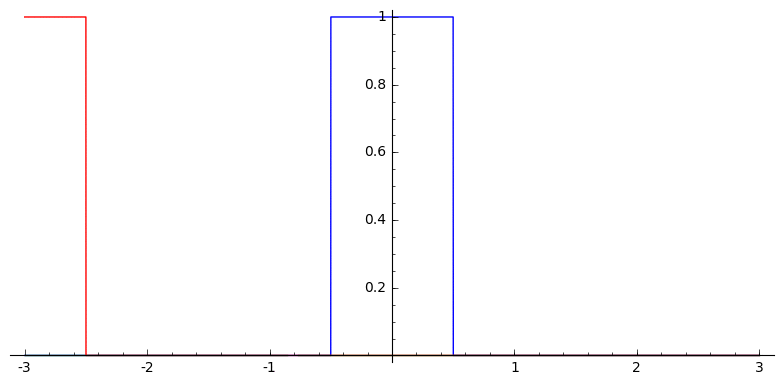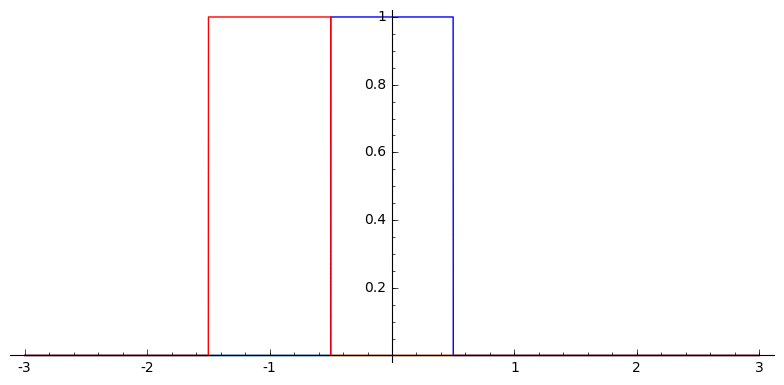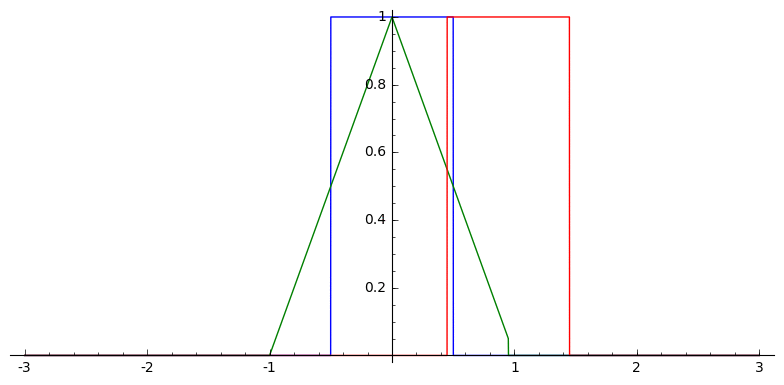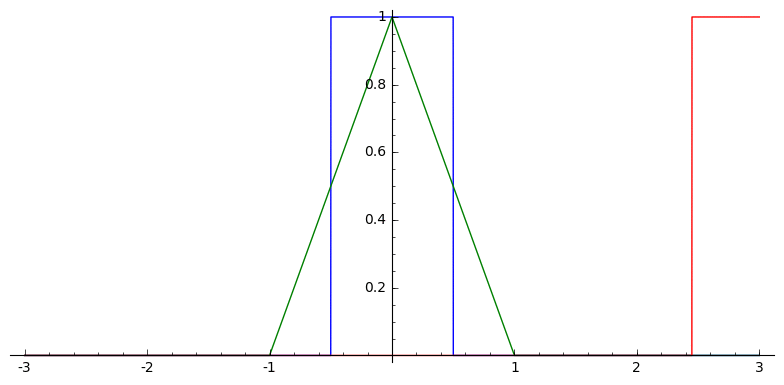
Voronoi Splines

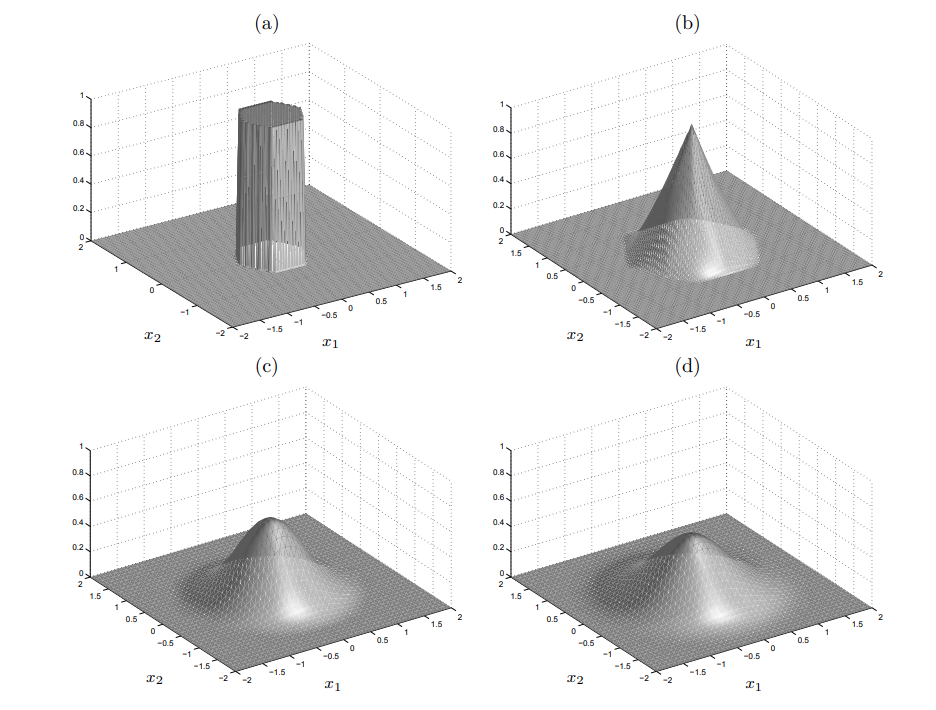
Voronoi Splines

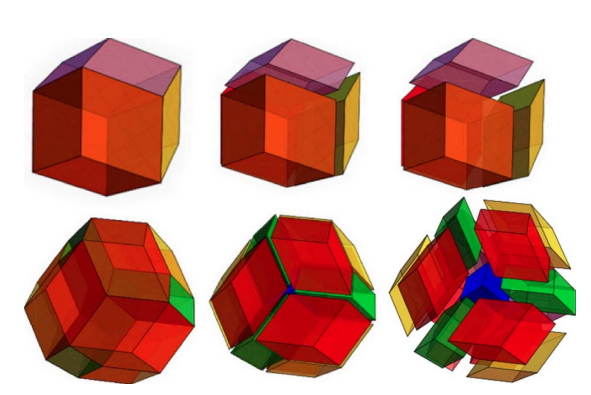
FCC

BCC

Generic Evaluation

f(x) = \displaystyle\sum_{n\in\overline{supp(\varphi(\cdot - x))} \cap \mathbb{Z}^3 }c_n \ \varphi(x-n) \chi_{L\mathbb{Z}^3}(n)

Lattice

Basis Function

Take this description, and ''generate code'' for it.

LLVM

A series of tools that transforms a low level representation (LLVM-IR) into functionally equivalent LLVM-IR.

What LLVM actually is, is quite vague.

....and backend code generators for various architectures.

Low level virtual machine

LLVM

Traditional compiler design is somewhat adhoc

Internal representation -> Optimization -> Code Generation

High Level Language

LLVM-IR

LLVM-IR

Optimization Passes

Front-end Compiler

Target Back-end 

Machine Code

Language designers only need to focus on high level semantics.

LLVM

LLVM-IR Crash Course

LLVM feels like a low level assembly language

define i32 @mul_add(i32 %x, i32 %y, i32 %z) {
entry:
  %tmp = mul i32 %x, %y
  %tmp2 = add i32 %tmp, %z
  ret i32 %tmp2
}

Although, it looks like assembly, there is no concept of a 'register'. Single static assignment --- variables are assigned once, and it is up to the backend to do register allocation.

LLVM

LLVM-IR Crash Course

All code can be converted to SSA form, (with the addition of \(\phi\) functions.)

define i32 @mul_add(i32 %x, i32 %y, i32 %z) {
entry:
  %tmp = mul i32 %x, %y
  %tmp2 = add i32 %tmp, %z
  ret i32 %tmp2
}

Code is organized into basic blocks, control may be conditionally passed to those blocks

LLVM

LLVM-IR Crash Course

All code can be converted to SSA form, (with the addition of \(\phi\) functions.)

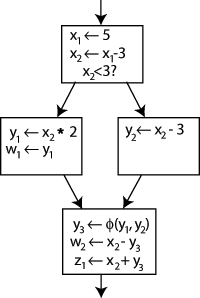
LLVM

LLVM-IR Crash Course


define i32 @phi_example(i32) #0 {
entry:
  %cmp = icmp sgt i32 %0, 0
  br i1 %cmp, label %case0, label %case1

case0:
  %tmp0 = add nsw i32 %0, 1
  br label %exit
case1:
  %tmp1 = sub nsw i32 %0, 1
  br label %exit

exit:
  %result = phi i32 [%tmp0, %case0], [%tmp1, %case1]
  ret i32 %result
}

LLVM

Optimization Passes

Transform LLVM-IR into (hopefully) functionally equvalent forms.

The main tool for this is opt, run opt --help for more information.

Dead code elimination, Global value numbering, fusing Instructions (you need to flag operations with fastmath for some of these) loop optimizations, etc...

LLVM

Target Backend

The tool here is llc, can specify the target backend

        .text
        .file   "e.ll"
        .globl  phi_example             # -- Begin function phi_example
        .p2align        4, 0x90
        .type   phi_example,@function
phi_example:                            # @phi_example
        .cfi_startproc
# %bb.0:                                # %entry
        movl    %edi, %eax
        testl   %edi, %edi
        jle     .LBB0_2
# %bb.1:                                # %case0
        incl    %eax
        retq
.LBB0_2:                                # %case1
        decl    %eax
        retq
.Lfunc_end0:
        .size   phi_example, .Lfunc_end0-phi_example
        .cfi_endproc
                                        # -- End function

        .section        ".note.GNU-stack","",@progbits

Can easily cross-compile to other architectures with -mcpu flag

LLVM

double horner_polynomial[] = {
  10., 2., 4., 0., 0., 0., 0., 1.
};

double horner_eval(double x) {
  double result = horner_polynomial[0];
  for (int i = 1; i < sizeof(horner_polynomial) / sizeof(double); i++) {
    result = result * x + horner_polynomial[i];
  }
  return result;
}

An illustrative example, recall Horner's method

\({\displaystyle {\begin{aligned}a_{0}&+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\&=a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}\,\end{aligned}}}\)

LLVM

An Example

import llvmlite.ir as ll         # You'll need to install llvmlite to run this
import llvmlite.binding as llvm

llvm.initialize()
llvm.initialize_native_target()
llvm.initialize_native_asmprinter()

def build_llvm_code(horner_polynomial):
    module  = ll.Module()
    func_ty = ll.FunctionType(ll.DoubleType(), [ll.DoubleType()])

    func = ll.Function(module, func_ty, name='horner_eval')
    bb = func.append_basic_block('entry')
	
    irbuilder = ll.IRBuilder(bb)
    result = ll.DoubleType()(horner_polynomial[0])
	
    for coeff in horner_polynomial[1:]:
        result = irbuilder.fmul(func.args[0], result)
        if coeff != 0:
            result = irbuilder.fadd(result, ll.DoubleType()(coeff))
    
    irbuilder.ret(result)
    return str(module)

build_llvm_code([10, 2, 4, 0, 0, 0, 0, 1])

LLVM

An Example

; ModuleID = ""
target triple = "x86_64-unknown-unknown"
target datalayout = ""

define double @"horner_eval"(double %".1") 
{
entry:
  %".3" = fmul double %".1", 0x4024000000000000
  %".4" = fadd double %".3", 0x4000000000000000
  %".5" = fmul double %".1", %".4"
  %".6" = fadd double %".5", 0x4010000000000000
  %".7" = fmul double %".1", %".6"
  %".8" = fmul double %".1", %".7"
  %".9" = fmul double %".1", %".8"
  %".10" = fmul double %".1", %".9"
  %".11" = fmul double %".1", %".10"
  %".12" = fadd double %".11", 0x3ff0000000000000
  ret double %".12"
}

LLVM

An Example

        .text
        .file   "example.ll"
        .section        .rodata.cst8,"aM",@progbits,8
        .p2align        3               # -- Begin function horner_eval
.LCPI0_0:
        .quad   4621819117588971520     # double 10
.LCPI0_1:
        .quad   4611686018427387904     # double 2
.LCPI0_2:
        .quad   4616189618054758400     # double 4
.LCPI0_3:
        .quad   4607182418800017408     # double 1
        .text
        .globl  horner_eval
        .p2align        4, 0x90
        .type   horner_eval,@function
horner_eval:                            # @horner_eval
        .cfi_startproc
# %bb.0:                                # %entry
        movsd   .LCPI0_0(%rip), %xmm1   # xmm1 = mem[0],zero
        mulsd   %xmm0, %xmm1
        addsd   .LCPI0_1(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   .LCPI0_2(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        mulsd   %xmm0, %xmm1
        mulsd   %xmm0, %xmm1
        mulsd   %xmm0, %xmm1
        mulsd   %xmm1, %xmm0
        addsd   .LCPI0_3(%rip), %xmm0
        retq
.Lfunc_end0:
        .size   horner_eval, .Lfunc_end0-horner_eval
        .cfi_endproc
                                        # -- End function

        .section        ".note.GNU-stack","",@progbits

LLVM

An Example

        .file   "example.c"
        .text
        .p2align 4,,15
        .globl  horner_eval
        .type   horner_eval, @function
horner_eval:
.LFB0:
        .cfi_startproc
        movsd   horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   8+horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   16+horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   24+horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   32+horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   40+horner_polynomial(%rip), %xmm1
        mulsd   %xmm0, %xmm1
        addsd   48+horner_polynomial(%rip), %xmm1
        mulsd   %xmm1, %xmm0
        addsd   56+horner_polynomial(%rip), %xmm0
        ret
        .cfi_endproc
.LFE0:
        .size   horner_eval, .-horner_eval
        .globl  horner_polynomial
        .data
        .align 32
        .type   horner_polynomial, @object
        .size   horner_polynomial, 64
horner_polynomial:
        .long   0
        .long   1076101120
        .long   0
        .long   1073741824
        .long   0
        .long   1074790400
        .long   0
        .long   0
        .long   0
        .long   0
        .long   0
        .long   0
        .long   0
        .long   0
        .long   0
        .long   1072693248

LLVM

An Example

; ModuleID = ""
target triple = "unknown-unknown-unknown"
target datalayout = ""

define double @"horner_eval"(double %".1") 
{
entry:
  %".3" = fmul double %".1", 0x4024000000000000
  %".4" = fadd double %".3", 0x4000000000000000
  %".5" = fmul double %".1", %".4"
  %".6" = fadd double %".5", 0x4010000000000000
  %".7" = fmul double %".1", %".6"
  %".8" = fadd double %".7",              0x0
  %".9" = fmul double %".1", %".8"
  %".10" = fadd double %".9",              0x0
  %".11" = fmul double %".1", %".10"
  %".12" = fadd double %".11",              0x0
  %".13" = fmul double %".1", %".12"
  %".14" = fadd double %".13",              0x0
  %".15" = fmul double %".1", %".14"
  %".16" = fadd double %".15", 0x3ff0000000000000
  ret double %".16"
}

Returning to my application

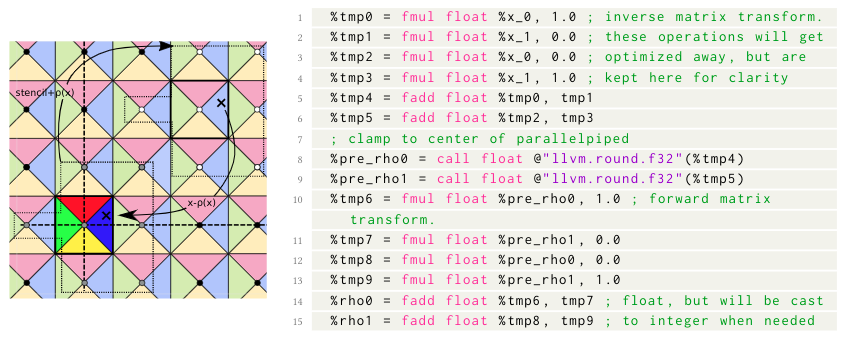
Shift to reference region

Sub-region Indexing

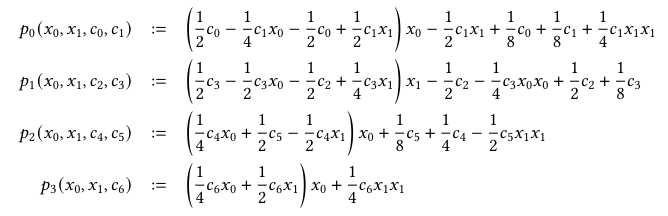
Pipelining

Example

Pipeline depth = 2, fetches in flight = 4

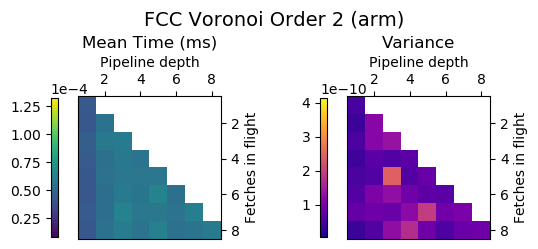
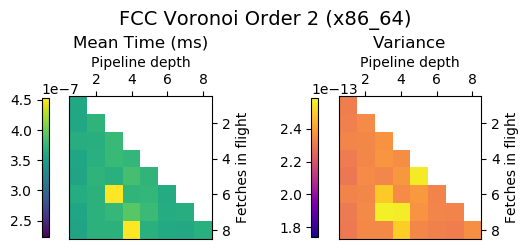
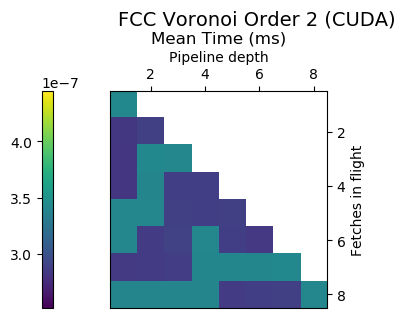
Experiment Setup

Choose a bunch of different splines.

Generate code for all possible combinations of FIF and PD on various architectures. Collect average time to reconstruct a single value.

Ryzen 9 3900X (x86_64), Raspberry Pi 2 (armv6), RTX 2070 Super (PTX or CUDA)

Second Order Splines

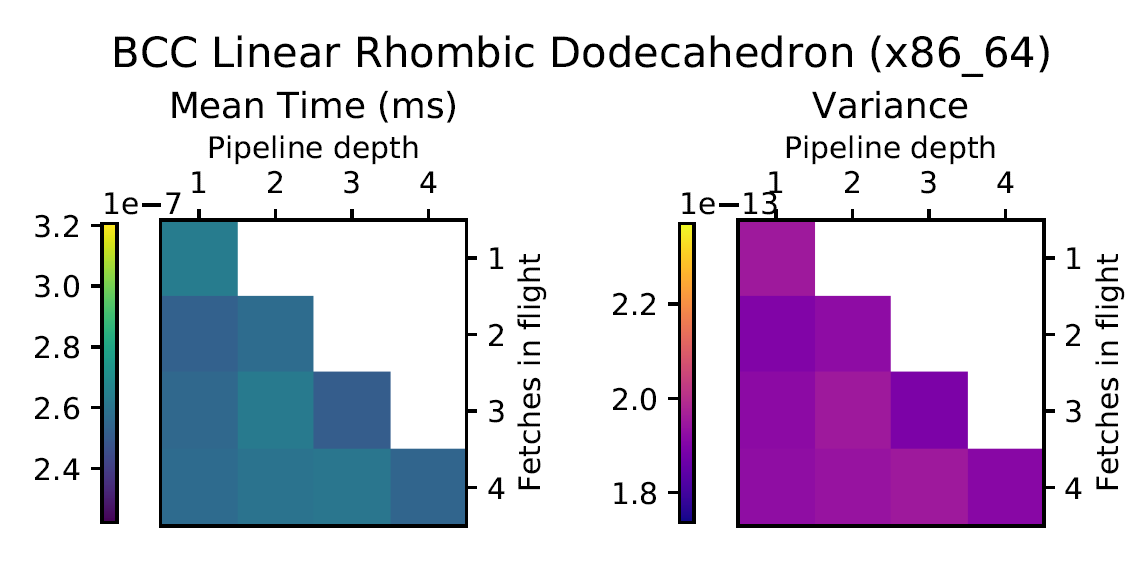
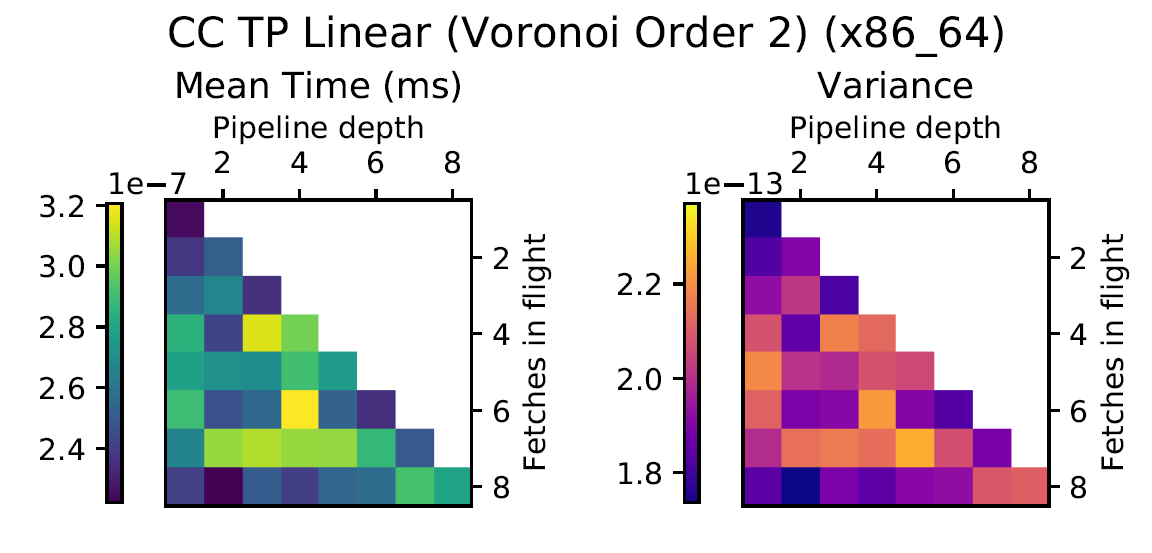
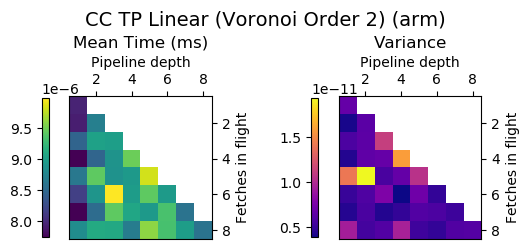
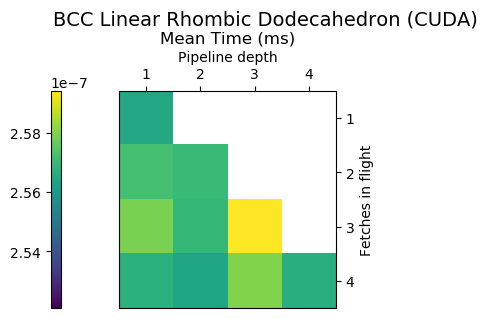
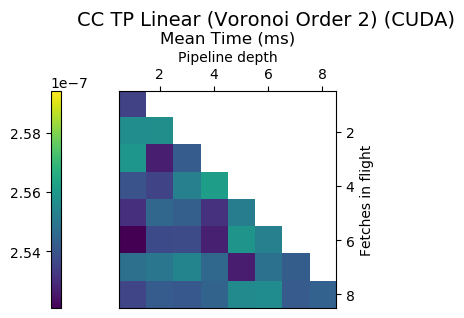
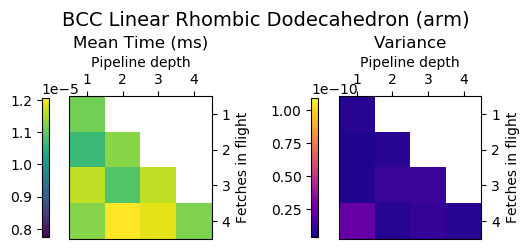
Third Order Splines

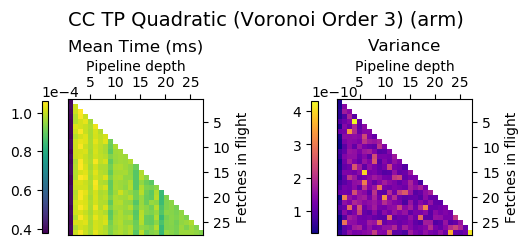
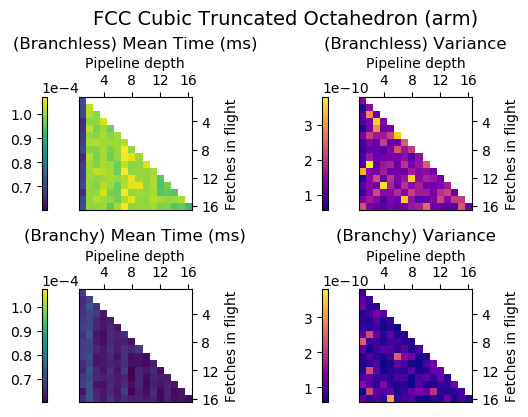
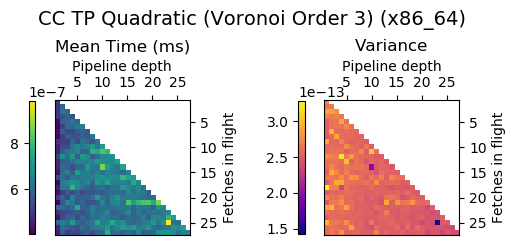
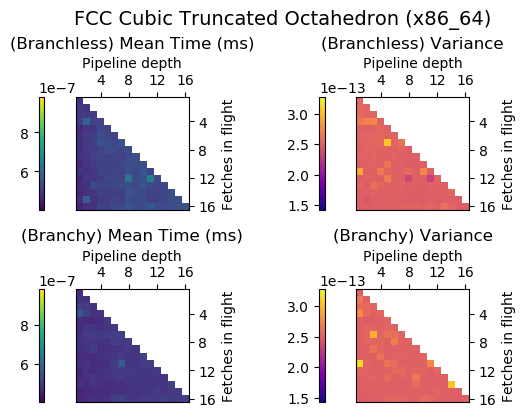
Voronoi Splines (2nd order)

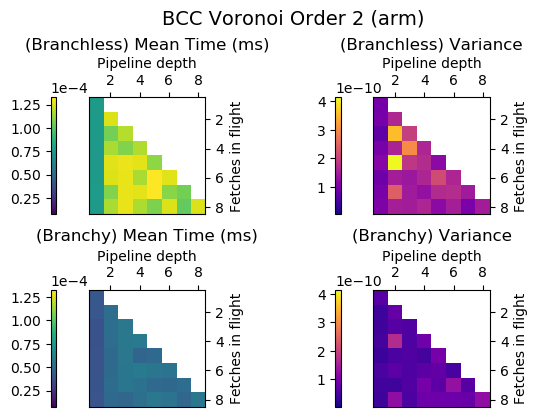
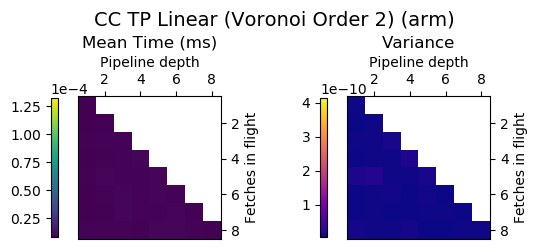
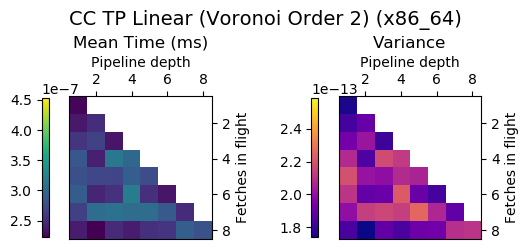
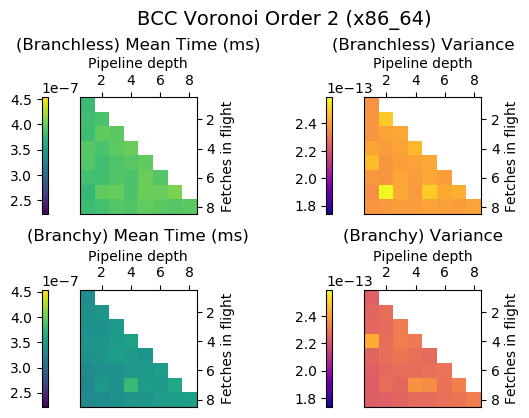
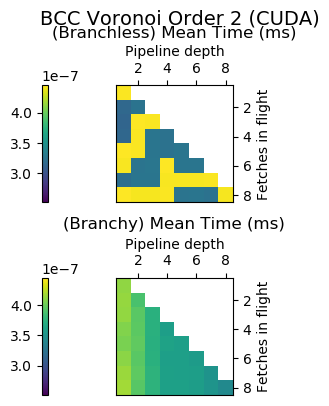
Voronoi Splines (2nd order)