Simulation-Efficient Implicit Inference with Differentiable Simulators

Justine Zeghal, François Lanusse, Alexandre Boucaud, Denise Lanzieri

Cosmic Connections: A ML X Astrophysics Symposium at Simons Foundation

 

May 22 - 24, New York City, United States

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

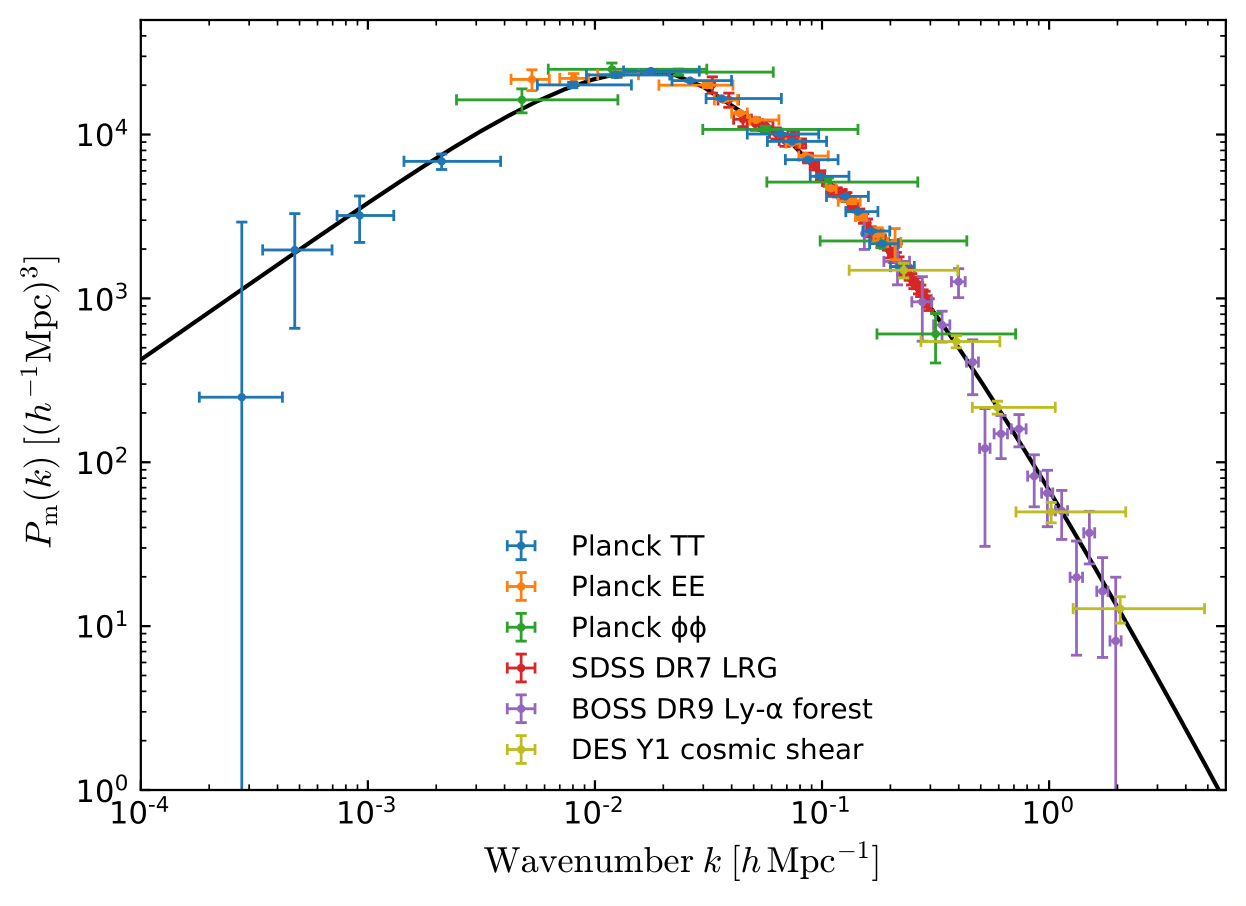
ESA and the Planck Collaboration, 2018

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Cosmological context

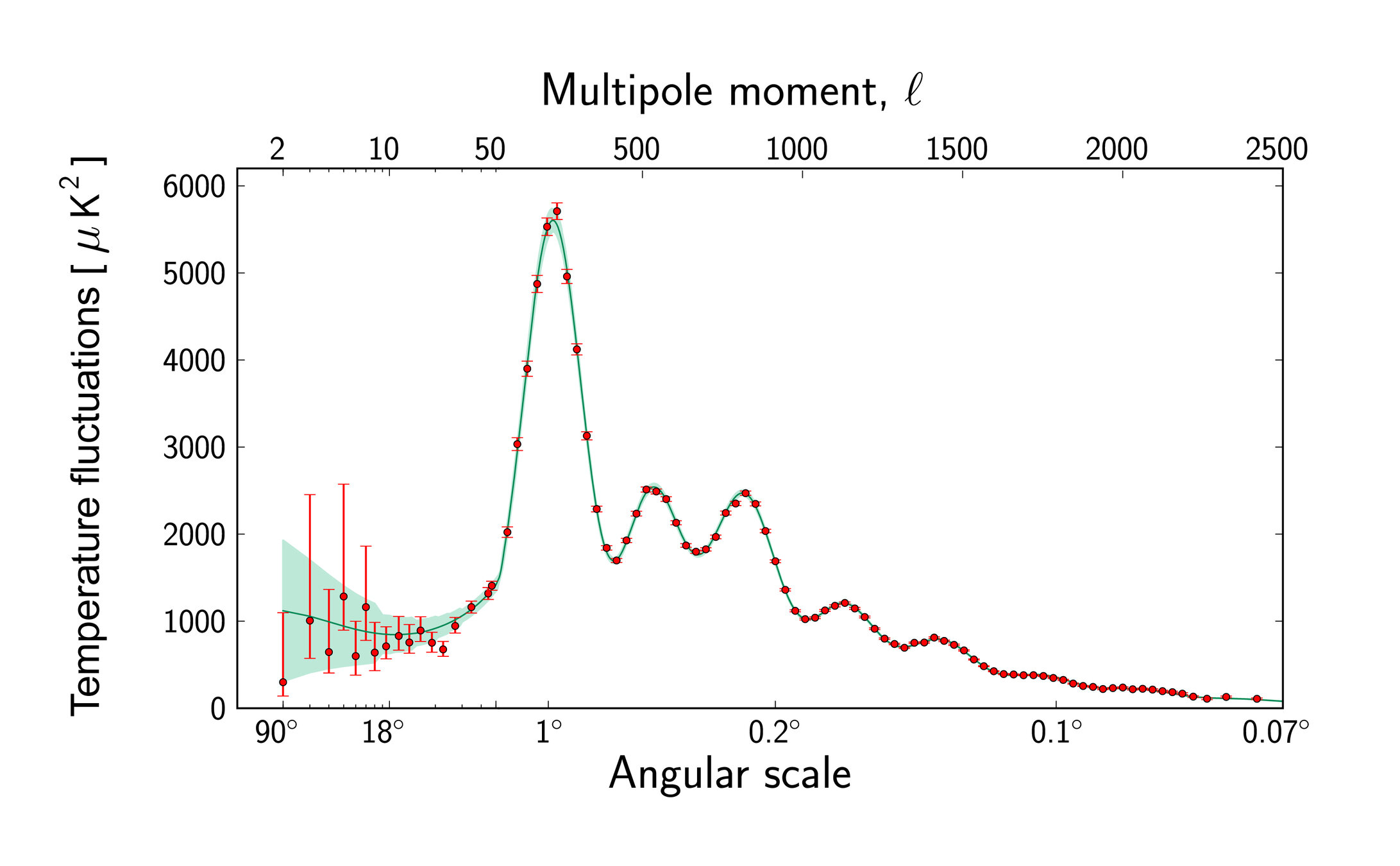
How to extract all the information embedded in our data?

Full-Field Inference

working at the pixel level

Downsides:

  • Computationally expensive (HMC)

Our Goal: doing Neural Posterior Estimation (Implicit Inference) with a minimum number of simulations.


 

  • Require a large number of simulations

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

  • We developed a differentiable (JAX) log-normal mass maps simulator

Differentiable Mass Maps Simulator
 

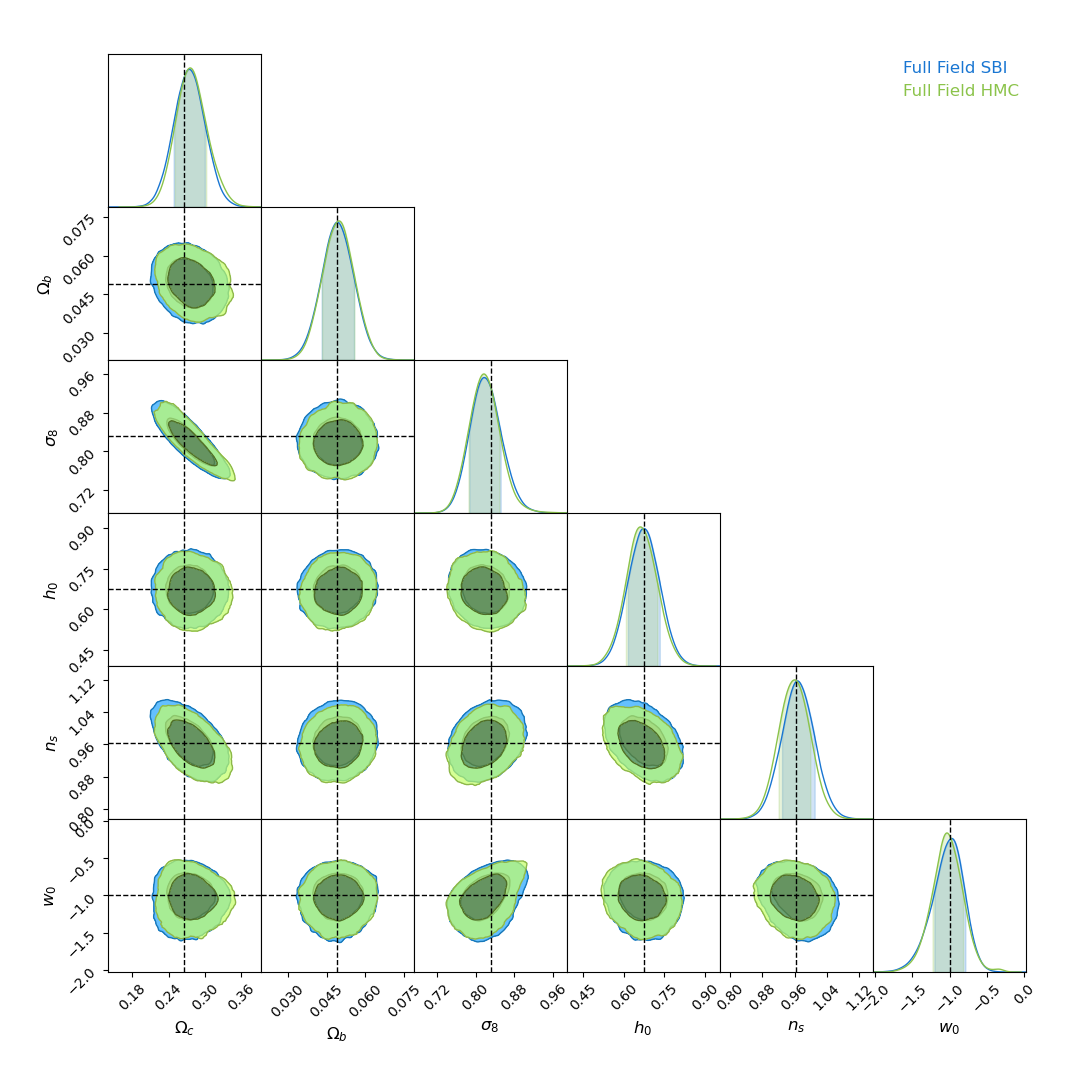
  • There is indeed more information to extract!

  • With infinite number of simulations, our Implicit Inference contours are as good as the Full-Field contours obtained through HMC


     

sbi_lens

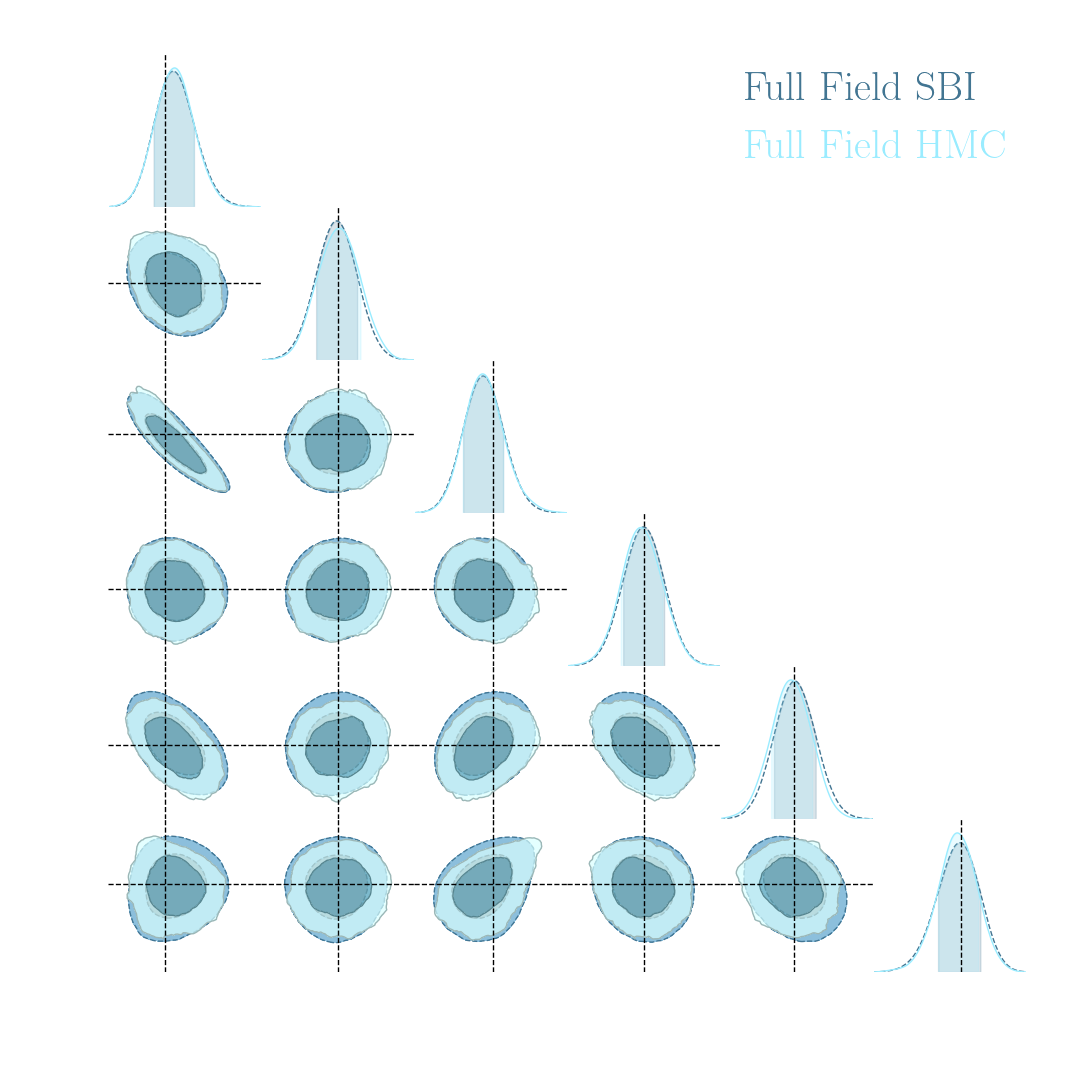
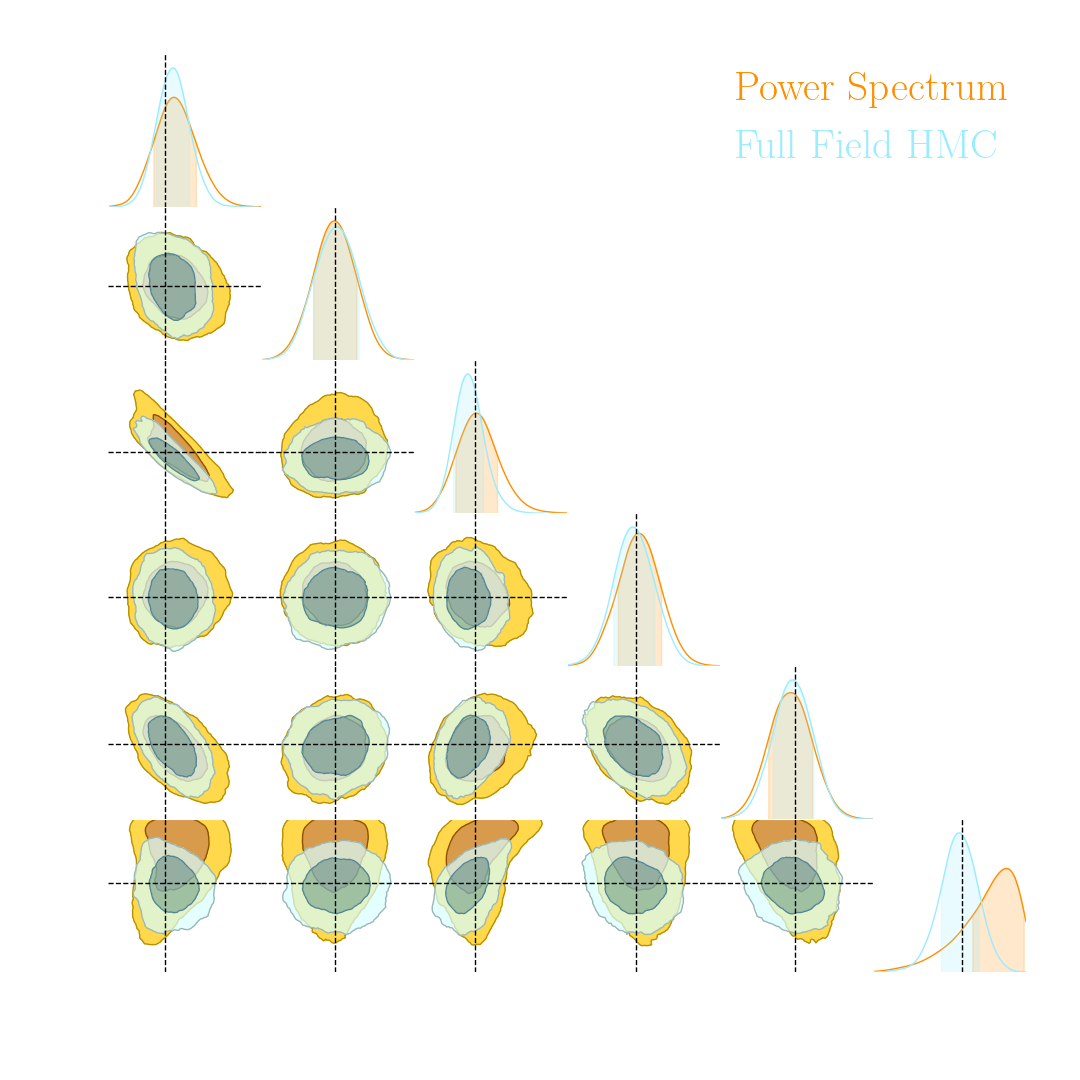
How can we reduce this number of simulations?

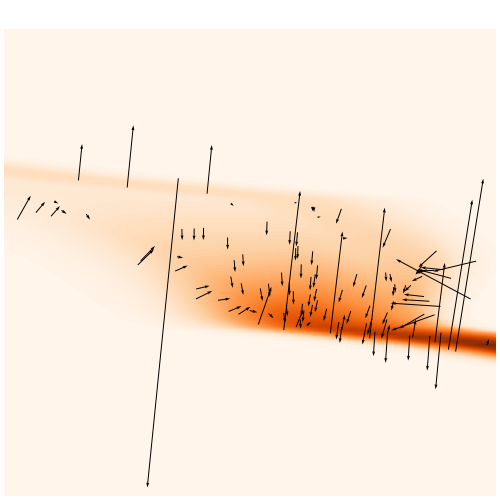
Gradient constraining power

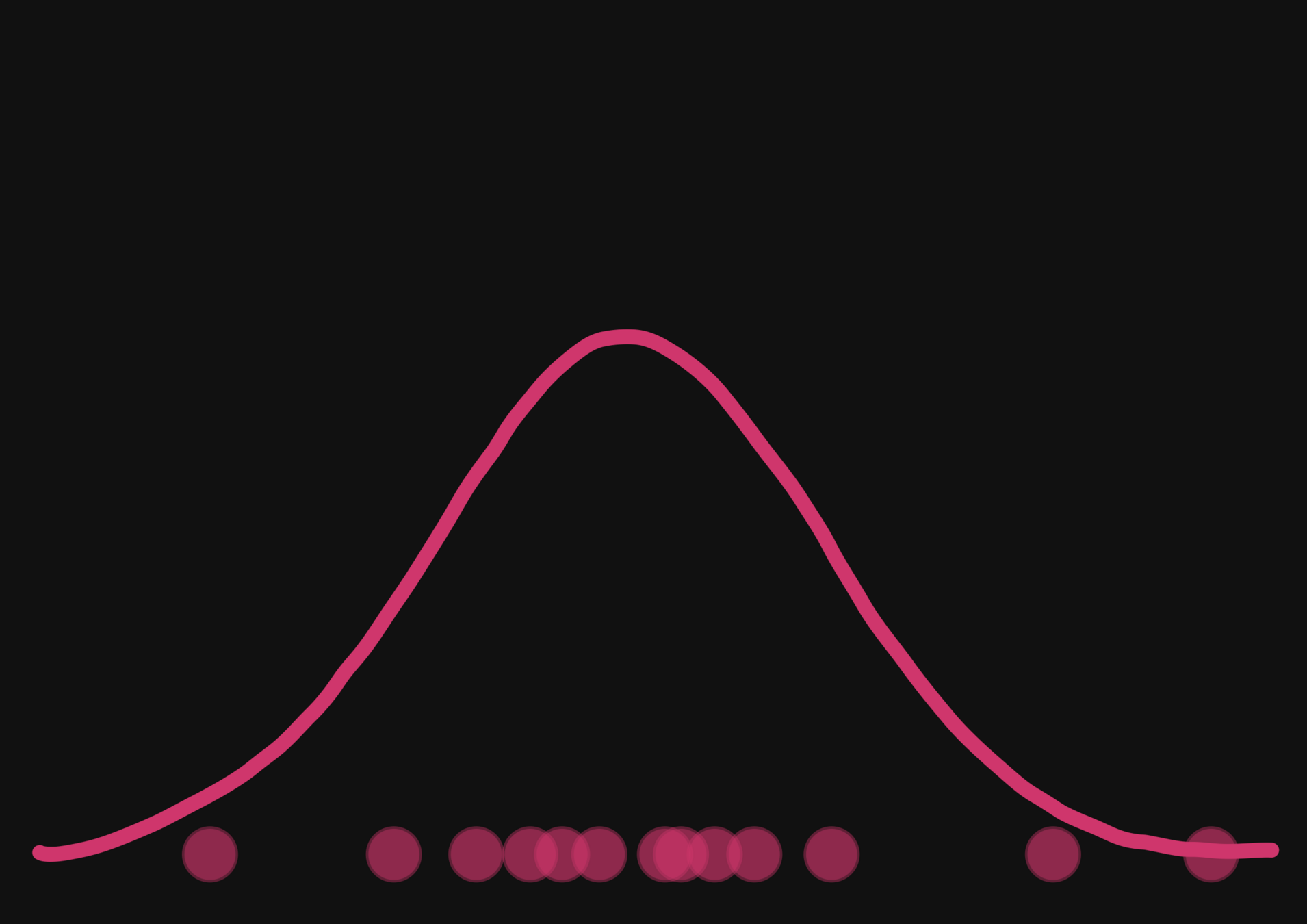
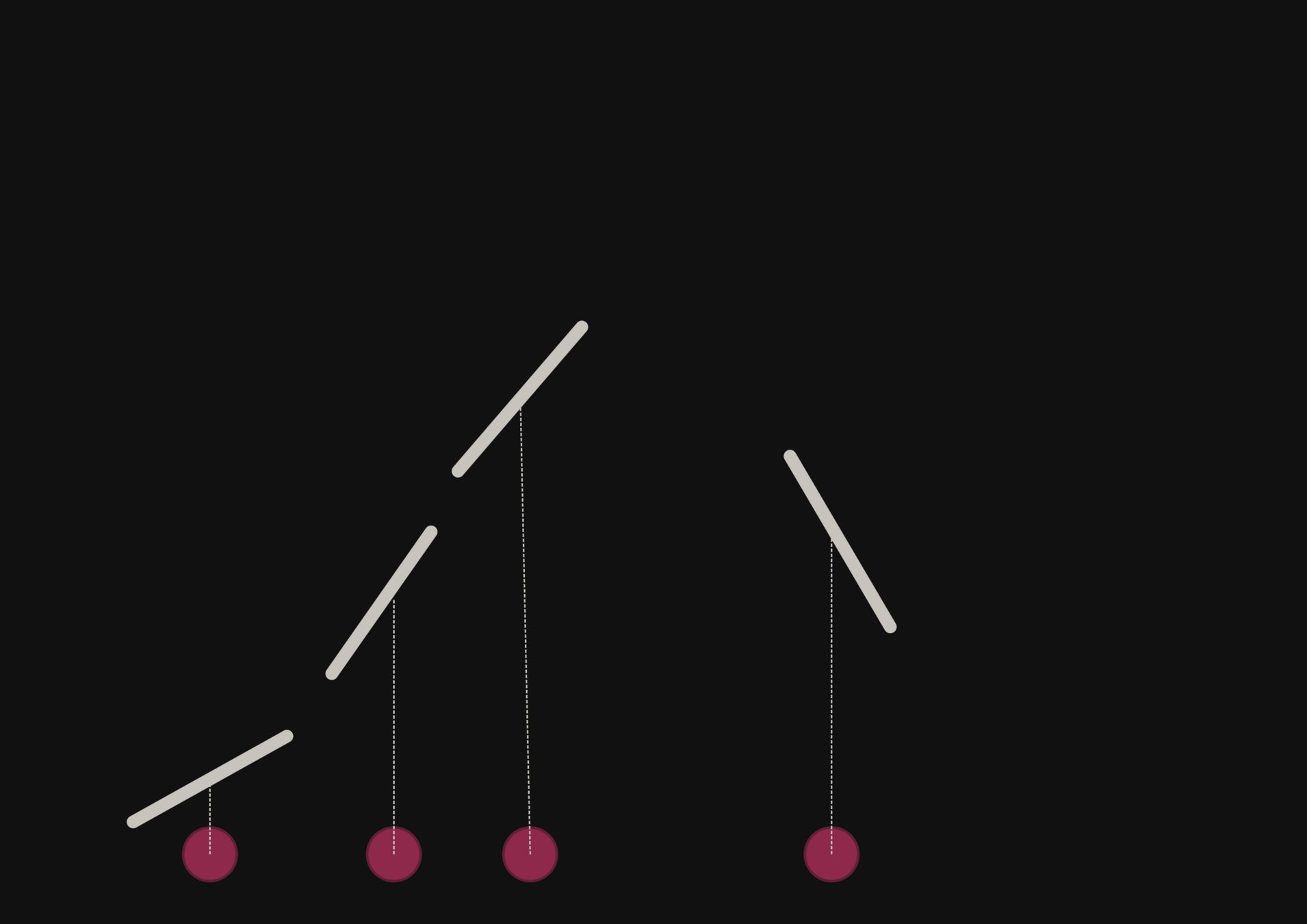
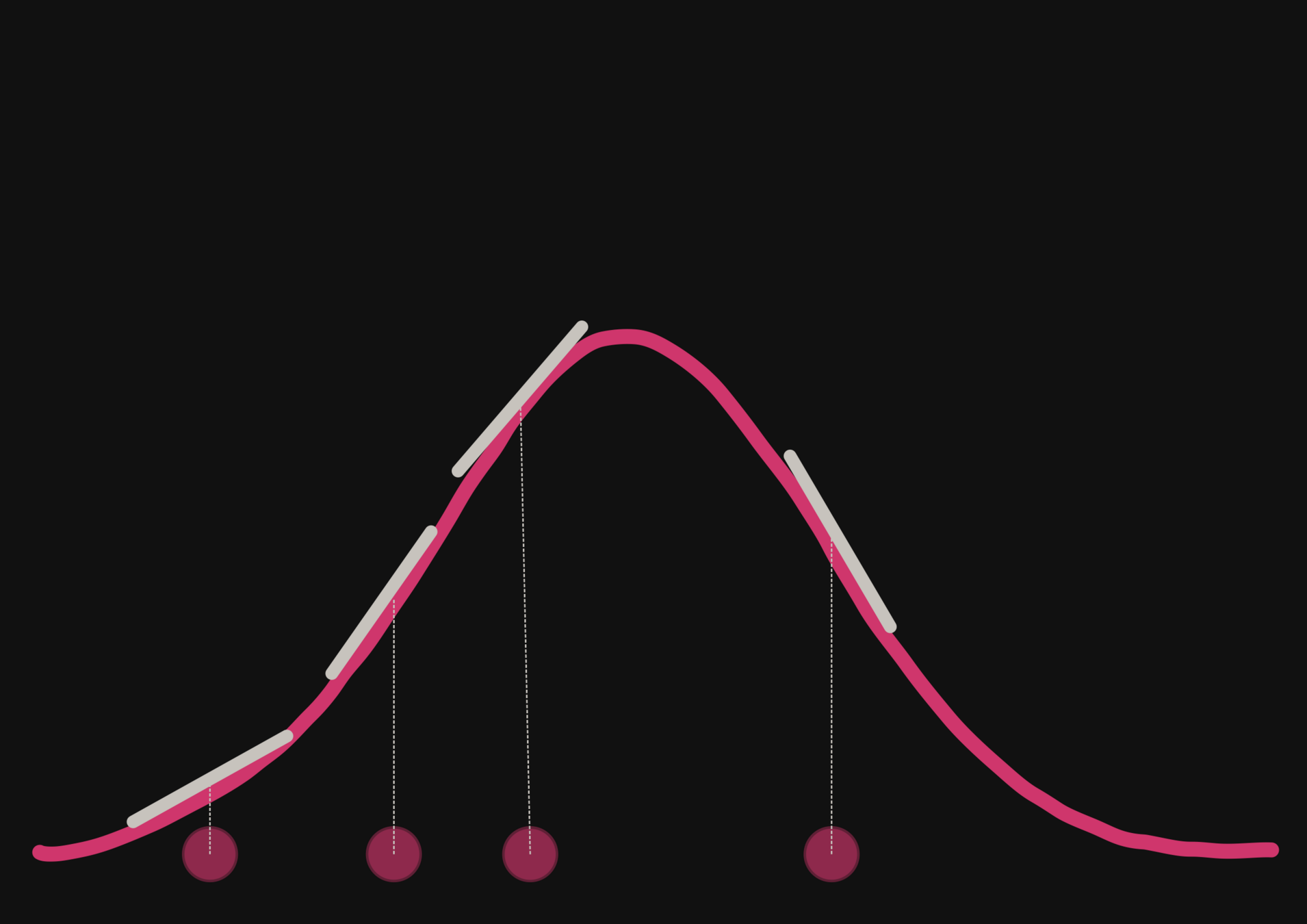
With a few simulations it's hard to approximate the posterior distribution.

→ we need more simulations

BUT if we have a few simulations

and the gradients

 

(also know as the score)

\nabla_{\theta} \log p(\theta|x)

Following this idea from Brehmer et al. 2019  we add the gradients of joint log probability of the simulator with respect to input parameters in the process

then it's possible to have an idea of the shape of the distribution.

Normalizing Flows (NFs) as Neural Density Estimators

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

Problem: the gradient of current NFs lack expressivity

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

Problem: the gradient of current NFs lack expressivity

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

Problem: the gradient of current NFs lack expressivity

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

Problem: the gradient of current NFs lack expressivity

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

But to train the NF, we want to use both simulations and gradients

Nfs are usually trained by minimizing the negative log likelihood loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]

Normalizing Flows (NFs) as Neural Density Estimators

Problem: the gradient of current NFs lack expressivity

Results from our previous paper

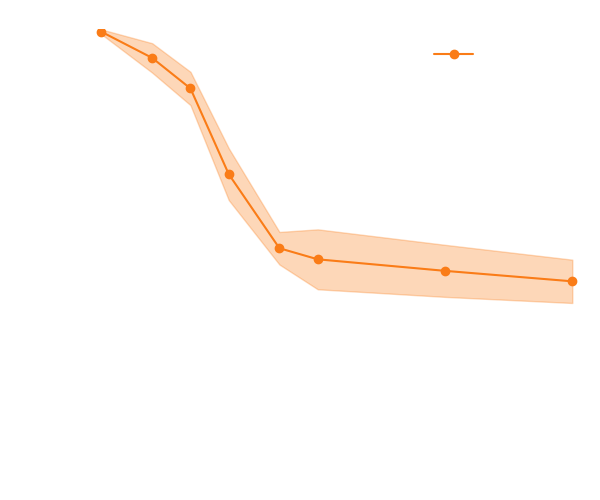
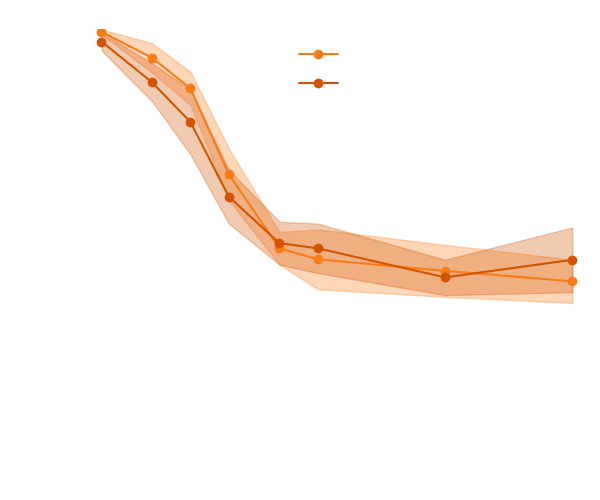
 Wide proposal distribution

 Narrow proposal distribution

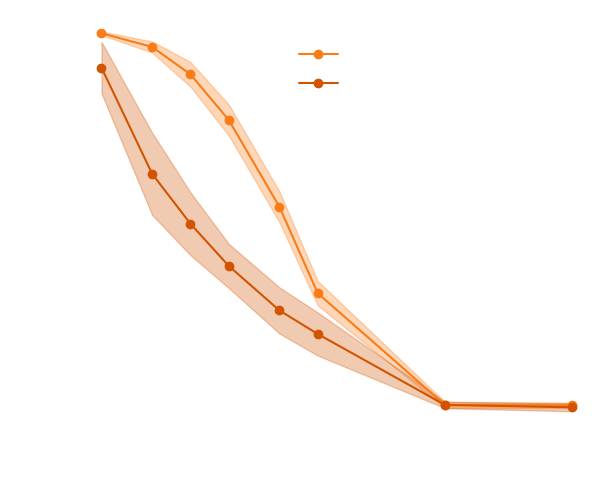
→ The score helps to constrain the distribution shape

Zeghal, Lanusse, Boucaud et al., 2022

Cosmological application

Since the score helps to constrain the shape, we start from the power spectrum posterior

Cosmological application

Since the score helps to constrain the shape, we start from the power spectrum posterior

\frac{p(\theta) \: \tilde{p}(x)}{\tilde{p}(\theta) \: p(x)}
p(\theta | x) = \tilde{p}(\theta | x)

Cosmological application

Since the score helps to constrain the shape, we start from the power spectrum posterior

\frac{p(\theta) \: \tilde{p}(x)}{\tilde{p}(\theta) \: p(x)}
p(\theta | x) = \tilde{p}(\theta | x)
- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

We adapt the previous loss:

Cosmological application

Since the score helps to constrain the shape, we start from the power spectrum posterior

\frac{p(\theta) \: \tilde{p}(x)}{\tilde{p}(\theta) \: p(x)}
p(\theta | x) = \tilde{p}(\theta | x)

We adapt the previous loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

Cosmological application

Since the score helps to constrain the shape, we start from the power spectrum posterior

\frac{p(\theta) \: \tilde{p}(x)}{\tilde{p}(\theta) \: p(x)}
p(\theta | x) = \tilde{p}(\theta | x)

We adapt the previous loss:

- \mathbb{E}_{p(x)}\left[ \log\left(p_x^{\phi}(x)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{x} \log p_x(x) - \underbrace{\nabla_x \log p_x^{\phi}(x)}\parallel_2^2 \right]

Preliminary

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Goal: approximate the posterior

Summary

Problem: we don't have an analytic marginalized likelihood

Goal: approximate the posterior

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\underbrace{p(\theta)}_{\text{prior}}
\propto

Summary

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Problem: we don't have an analytic marginalized likelihood

Summary

→ need new methods to extract all informations

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

→ Full-Field Inference

→ need new methods to extract all informations

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

Summary

→ computationally expensive + large number of simulations

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

→ Full-Field Inference

→ need new methods to extract all informations

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

Summary

directly approximate the posterior (NPE): no need for MCMCs

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

→

→ computationally expensive + large number of simulations

→ Full-Field Inference

→ need new methods to extract all informations

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

directly approximate the posterior (NPE): no need for MCMCs

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

directly approximate the posterior (NPE): no need for MCMCs

→

→ computationally expensive + large number of simulations

→ Full-Field Inference

→ need new methods to extract all informations

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

directly approximate the posterior (NPE): no need for MCMCs

SBI with gradients

→

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

directly approximate the posterior (NPE): no need for MCMCs

→

→ computationally expensive + large number of simulations

→ Full-Field Inference

→ need new methods to extract all information

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

directly approximate the posterior (NPE): no need for MCMCs

SBI with gradients

→

⚠️  requirements: differentiable simulator + smooth NDE

Summary

\underbrace{p(\theta|x)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x|\theta)}_{\text{likelihood}}
\propto

directly approximate the posterior (NPE): no need for MCMCs

→

→ computationally expensive + large number of simulations

→ Full-Field Inference

→ need new methods to extract all information

Current methods: insufficient summary statistics + gaussian assumptions

Goal: approximate the posterior

Problem: we don't have an analytic marginalized likelihood

directly approximate the posterior (NPE): no need for MCMCs

Thank You!

⚠️  requirements: differentiable simulator + smooth NDE

SBI with gradients

→