Field-Level

Inference

Justine Zeghal

justine.zeghal@umontreal.ca

Learning the Universe meeting

October 2025

Université de Montréal

\underbrace{p(\theta|x=x_0)}_{\text{posterior}}
\underbrace{p(\theta)}_{\text{prior}}
\underbrace{p(x = x_0|\theta)}_{\text{likelihood}}
\propto

Bayes theorem:

We can build a simulator to map the cosmological parameters to the data.

Prediction

Inference

 Full-field inference: extracting all cosmological information

x
\theta

 Simulator

\underbrace{p(x = x_0|\theta)}_{\text{likelihood}}

Depending on the simulator’s nature  we can either perform

  • Explicit inference 
  • Implicit inference 

 Full-field inference: extracting all cosmological information

\theta

 Simulator

z
x

Initial conditions of the Universe

Large Scale Structure

p(\theta, z \: | \: x) \propto
p(z\:|\:\theta) p(\theta)

Needs an explicit simulator to sample the joint posterior through MCMC:

p(x| \theta, z)

We need to sample in

high-dimension

→ gradient-based sampling schemes

Credit:  Chirag Modi, François Lanusse, Mustafa Mustafa, Uroŝ Seljak

z
f
\sigma^2
\mathcal{N}

  • Explicit inference

x

Explicit joint likelihood

 

p(x| \theta, z)
(\theta_i, x_i)_{i=1...N}

This approach typically involve 2 steps:

2) Implicit inference on these summary statistics to approximate the posterior.

1) compression of the high dimensional data into summary statistics. Without loosing cosmological information!

Summary statistics

t = f_{\varphi}(x)
p_{\Phi}(\theta | f_{\varphi}(x))

 Full-field inference: extracting all cosmological information

\theta

 Simulator

  • Implicit inference

It does not matter if the simulator is explicit or implicit because all we need are simulations

x

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Optimal Neural Summarisation for Full-Field Weak Lensing Cosmological Implicit Inference

Denise Lanzieri*, Justine Zeghal*, T. Lucas Makinen, François Lanusse, Alexandre Boucaud and Jean-Luc Starck

t = f_{\varphi}(x)
\theta
p(\theta \: | \: x) = p(\theta \: | \: t) \: \text{ with } \: t=f(x)

It is only a matter of the loss function used to train the compressor.

 How to extract all the information?

Sufficient Statistic

A statistic t is said to be sufficient for the parameters    if and only if

x

 Two main compression schemes

\hat{\theta} = f_\varphi(x)

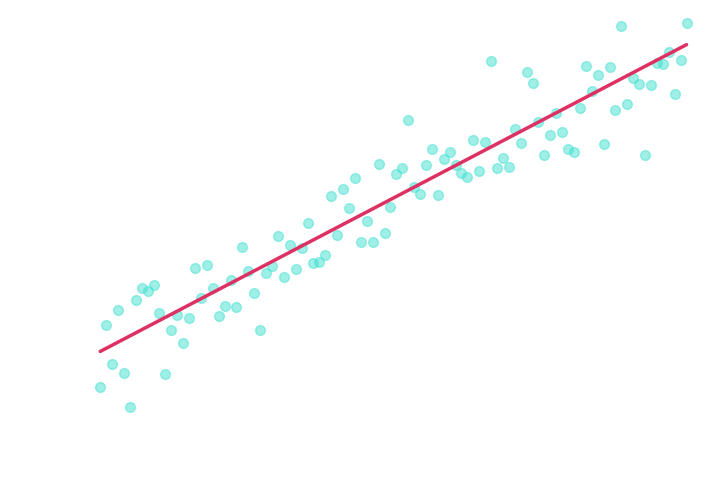
Regression Losses

 Two main compression schemes

\hat{\theta} = f_\varphi(x)

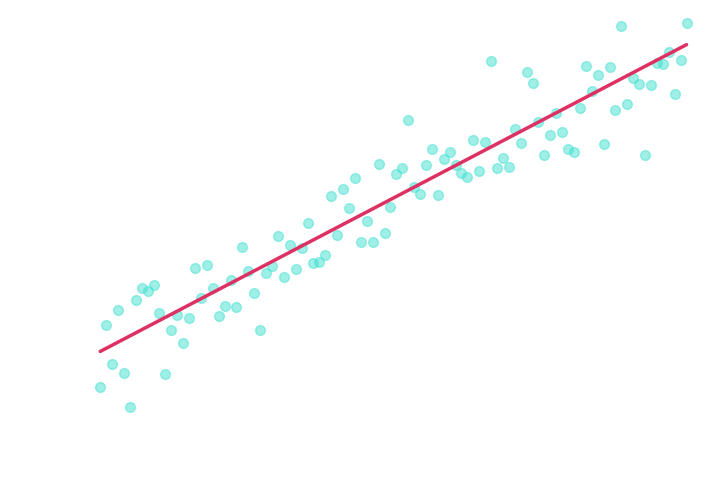
Regression Losses

Which learns a moment of the posterior distribution.

 Two main compression schemes

Mean Squared Error (MSE) loss:

\mathcal{L}_{\text{MSE}} = \mathbb{E}_{p(x,\theta)} \left[\parallel \theta - f_\varphi(x) \parallel ^2 \right]

Which learns a moment of the posterior distribution.

\hat{\theta} = f_\varphi(x)

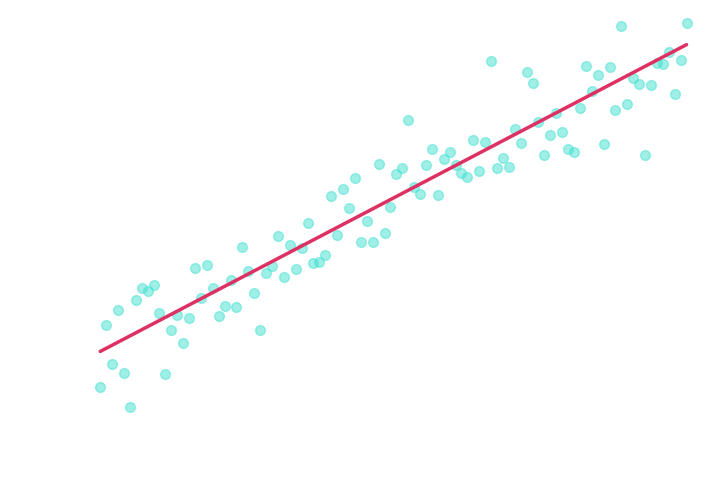
Regression Losses

 Two main compression schemes

\mathcal{L}_{\text{MSE}} = \mathbb{E}_{p(x,\theta)} \left[\parallel \theta - f_\varphi(x) \parallel ^2 \right]

→ Approximate the mean of the posterior.

\hat{\theta} = f_\varphi(x)

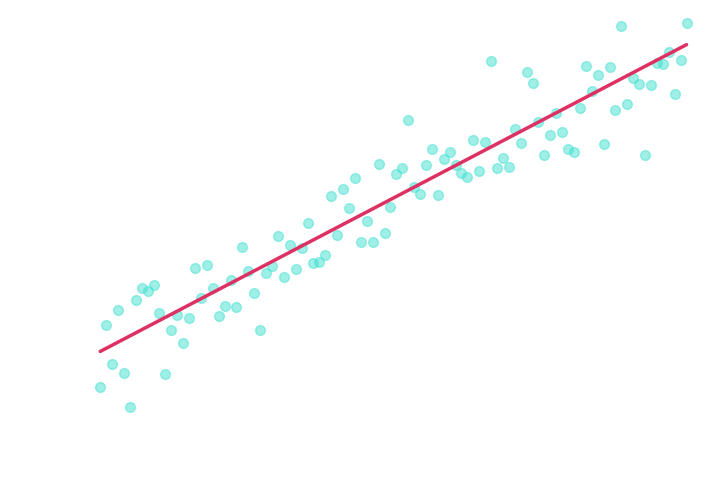
Which learns a moment of the posterior distribution.

 Two main compression schemes

Mean Squared Error (MSE) loss:

Regression Losses

\mathcal{L}_{\text{MSE}} = \mathbb{E}_{p(x,\theta)} \left[\parallel \theta - f_\varphi(x) \parallel ^2 \right]

→ Approximate the mean of the posterior.

\hat{\theta} = f_\varphi(x)

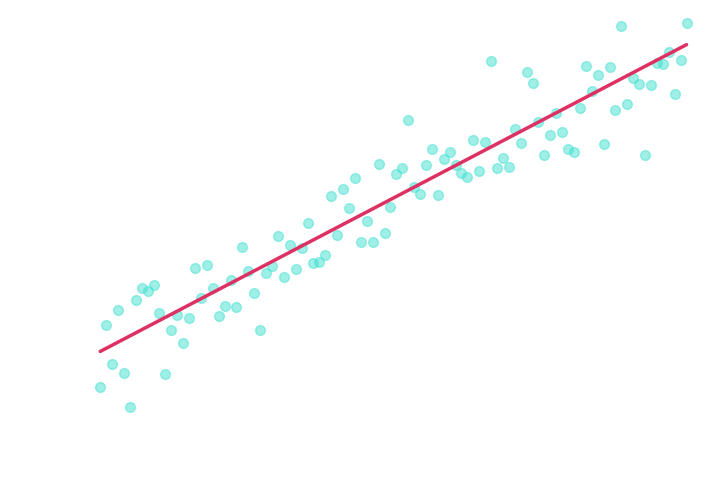
Mean Absolute Error (MAE) loss:

\mathcal{L}_{\text{MAE}} = \mathbb{E}_{p(x,\theta)} \left[| \theta - f_\varphi(x) |\right]

Which learns a moment of the posterior distribution.

 Two main compression schemes

Mean Squared Error (MSE) loss:

Regression Losses

→ Approximate the median of the posterior.

 Two main compression schemes

\mathcal{L}_{\text{MSE}} = \mathbb{E}_{p(x,\theta)} \left[\parallel \theta - f_\varphi(x) \parallel ^2 \right]

→ Approximate the mean of the posterior.

\hat{\theta} = f_\varphi(x)

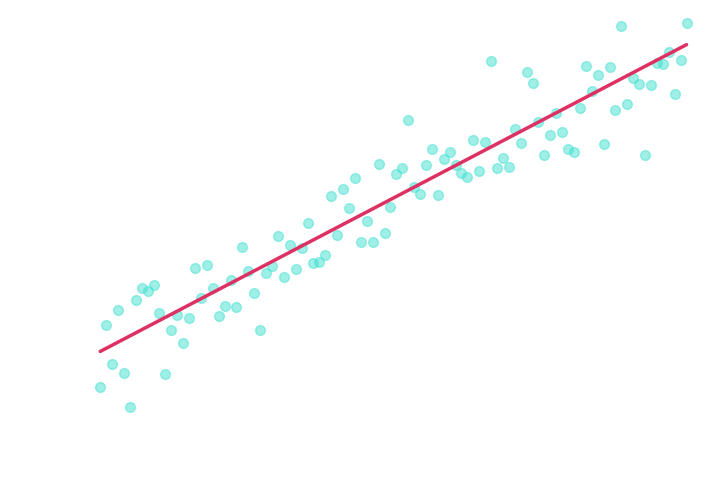
Mean Absolute Error (MAE) loss:

\mathcal{L}_{\text{MAE}} = \mathbb{E}_{p(x,\theta)} \left[| \theta - f_\varphi(x) |\right]

Which learns a moment of the posterior distribution.

Mean Squared Error (MSE) loss:

Regression Losses

Regression Losses

 Two main compression schemes

\mu_1 = \mu_2

 Two main compression schemes

Regression Losses

\mu_1 = \mu_2

 Two main compression schemes

Regression Losses

\mu_1 = \mu_2

 Two main compression schemes

Regression Losses

\mu_1 = \mu_2
\neq

The mean is not guaranteed to be a sufficient statistic.

 Two main compression schemes

Regression Losses

Mutual information maximization

 Two main compression schemes

p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

I(\theta,x)
H(\theta)
H(x)
H(\theta|x)
H(x|\theta)
I(\theta,x) = H(x) - H(x|\theta)
p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

I(\theta,x)
H(\theta)
H(x)
H(\theta|x)
H(x|\theta)
I(\theta,x) = H(x) - H(x|\theta)
p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

I(\theta,x)
H(\theta)
H(x)
H(\theta|x)
H(x|\theta)
I(\theta,x) = H(x) - H(x|\theta)
p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

I(\theta,x)
H(\theta)
H(x)
H(\theta|x)
H(x|\theta)
I(\theta,x) = H(x) - H(x|\theta)
p(\theta \: | \: x) = p(\theta \: | \: t(x)) \: \Leftrightarrow I(\theta, x) = I (\theta, t(x))

Mutual information maximization

By definition:

 Two main compression schemes

I(\theta,x)
H(\theta)
H(x)
H(\theta|x)
H(x|\theta)
I(\theta,x) = H(x) - H(x|\theta)

→ build sufficient statistics according to the definition.

We developed a fast and differentiable (JAX) log-normal mass maps simulator.

DifferentiableUniverseInitiative/​sbi-lens

 For our benchmark: a Differentiable Mass Maps Simulator

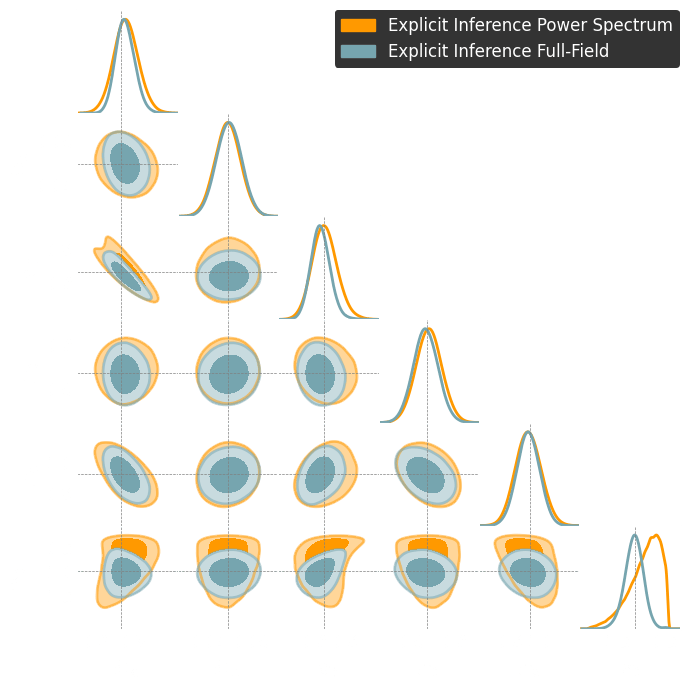
1. We compress using one of the losses.

Benchmark procedure:

2. We compare their extraction power by comparing their posteriors.

For this, we use implicit inference, which is fixed for all the compression strategies.

p(\theta \: | \: x) = p(\theta \: | \: t) \: \text{ with } \: t=f(x)

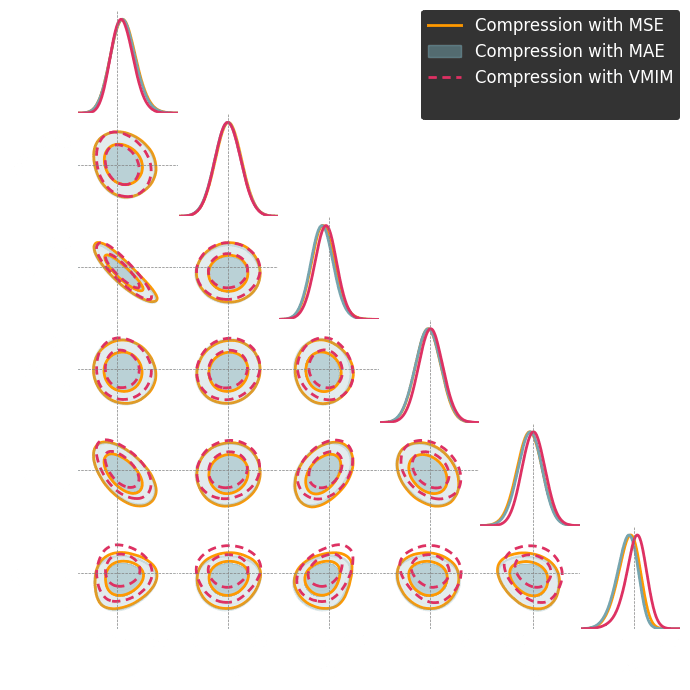
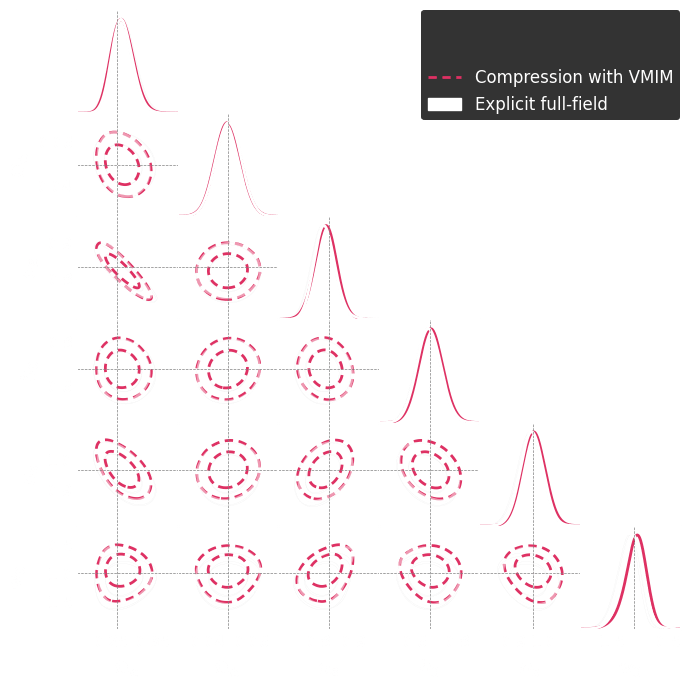
 Numerical results

DifferentiableUniverseInitiative/​sbi-lens

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Neural Posterior Estimation with Differentiable Simulators

ICML 2022 Workshop on Machine Learning for Astrophysics

 

Justine Zeghal, François Lanusse, Alexandre Boucaud,

Benjamin Remy and Eric Aubourg

 Neural Posterior Estimation

There exist several ways to do implicit inference

(\theta_i, x_i)_{i=1...N} \sim p(x, \theta)
  • Learning the likelihood
  • Learning the likelihood ratio
  • Learning the posterior

 Neural Posterior Estimation

→ Normalizing Flows

\begin{array}{ll} Loss = - \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta\mid x)\right) \right]\\ \end{array}

From simulations only!

A lot of simulations..

There exist several ways to do implicit inference

(\theta_i, x_i)_{i=1...N} \sim p(x, \theta)
  • Learning the likelihood
  • Learning the likelihood ratio
  • Learning the posterior

 Neural Posterior Estimation with Gradients

→ Normalizing Flows

\begin{array}{ll} Loss = - \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta\mid x)\right) \right]\\ \end{array}

From simulations only!

A lot of simulations..

There exist several ways to do implicit inference

(\theta_i, x_i)_{i=1...N} \sim p(x, \theta)

How gradients can help reduce the number of simulations?

(\theta_i, x_i, \nabla_\theta \log p(\theta \mid x_i))_{i=1...N}
  • Learning the likelihood
  • Learning the likelihood ratio
  • Learning the posterior

 Normalizing Flows training with gradients

Normalizing flows are trained by minimizing the negative log likelihood:

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

 Normalizing Flows training with gradients

But to train the NF, we want to use both simulations and the gradients from the simulator

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

Normalizing flows are trained by minimizing the negative log likelihood:

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

 Normalizing Flows training with gradients

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

But to train the NF, we want to use both simulations and the gradients from the simulator

Normalizing flows are trained by minimizing the negative log likelihood:

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

 Normalizing Flows training with gradients

+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta, z |x) - \nabla_{\theta} \log p^{\phi}(\theta |x)\parallel_2^2 \right]

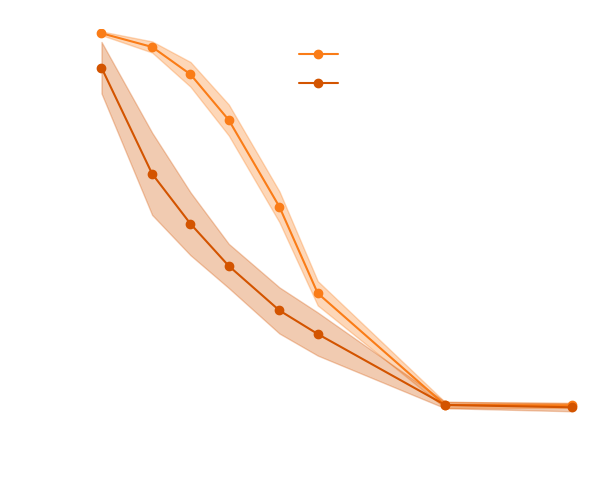
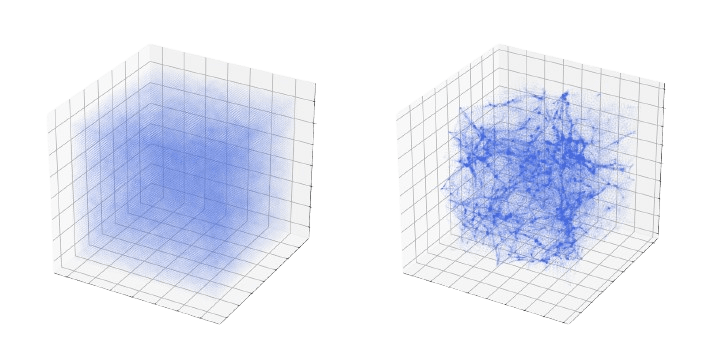
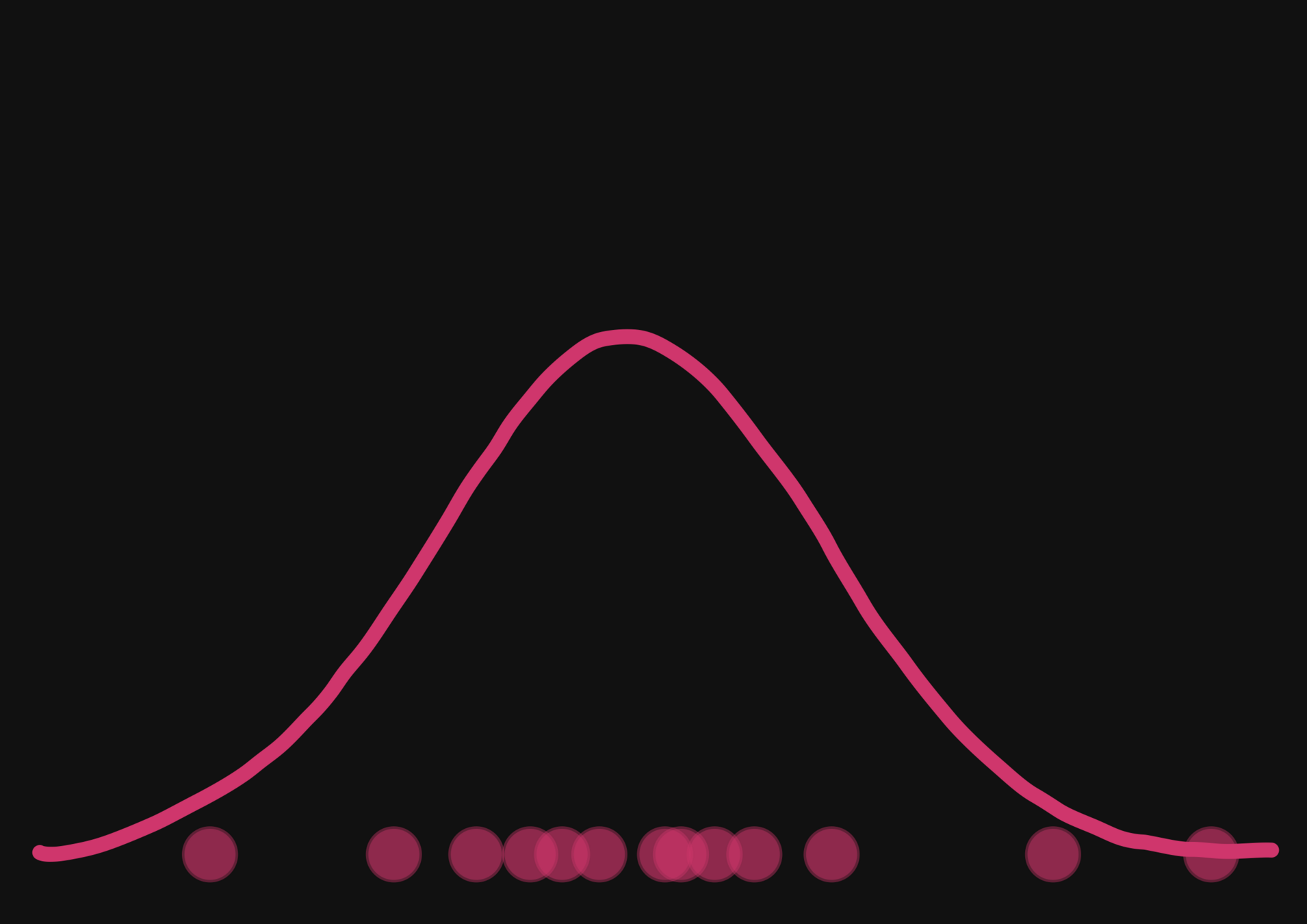
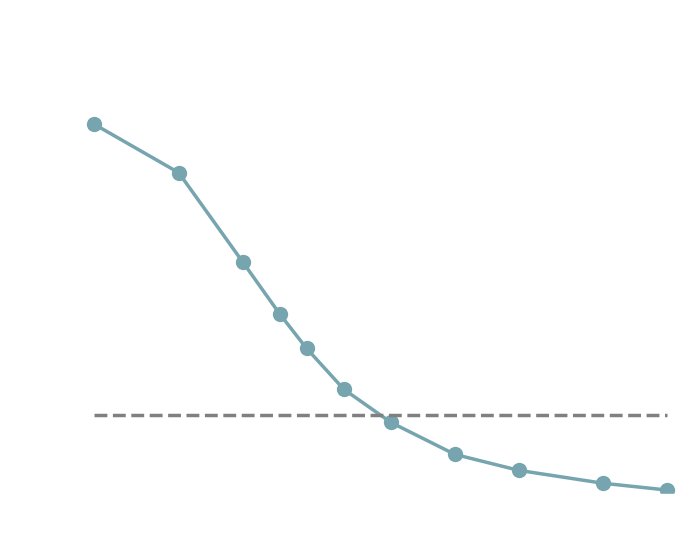
→ On a toy Lotka Volterra model, the gradients helps to constrain the distribution shape.

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(\theta | x)\right) \right]

But to train the NF, we want to use both simulations and the gradients from the simulator

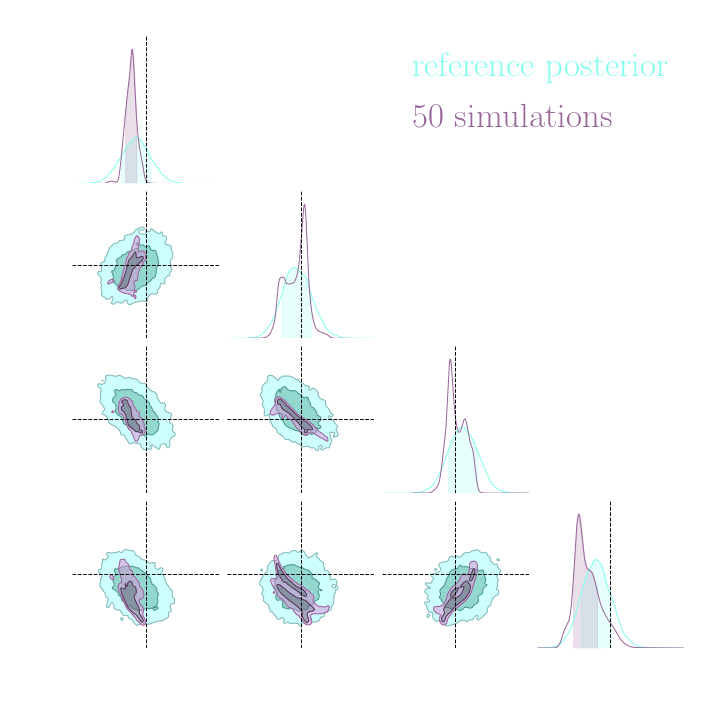
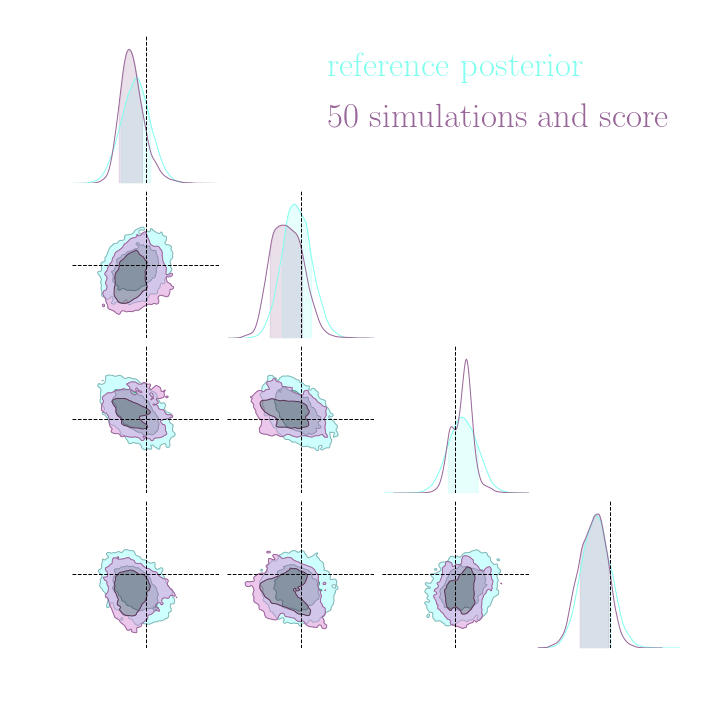
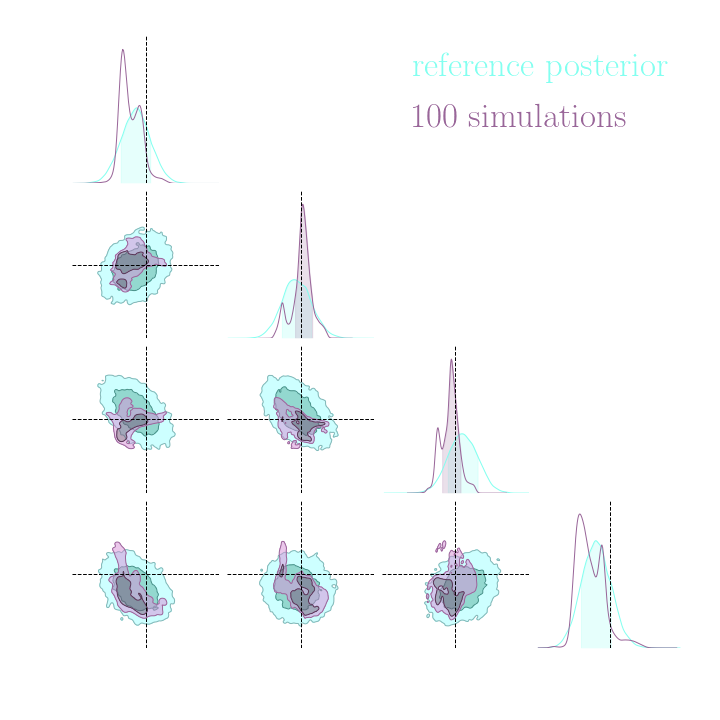
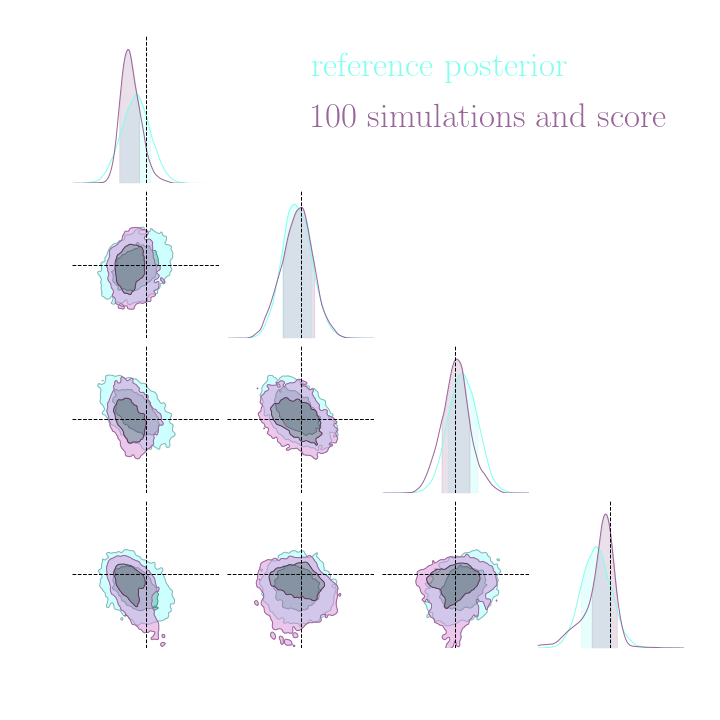
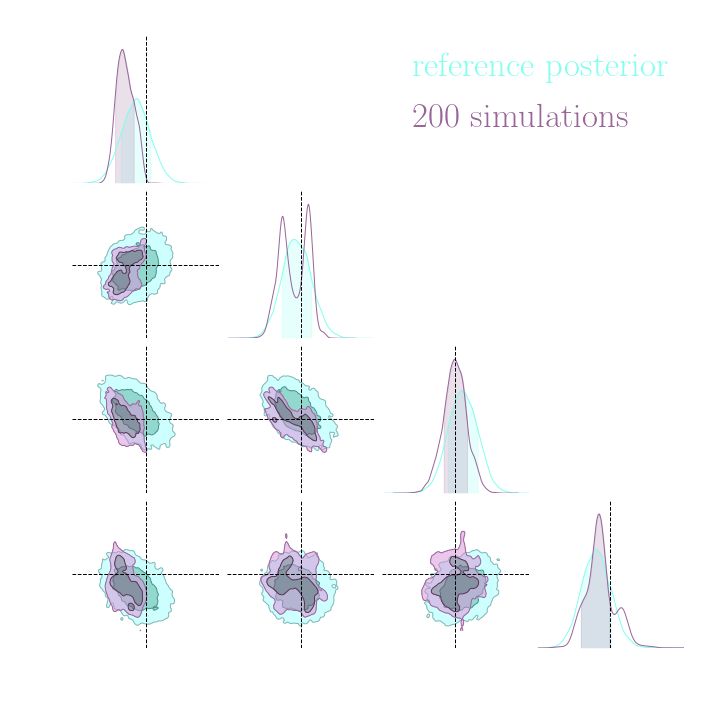
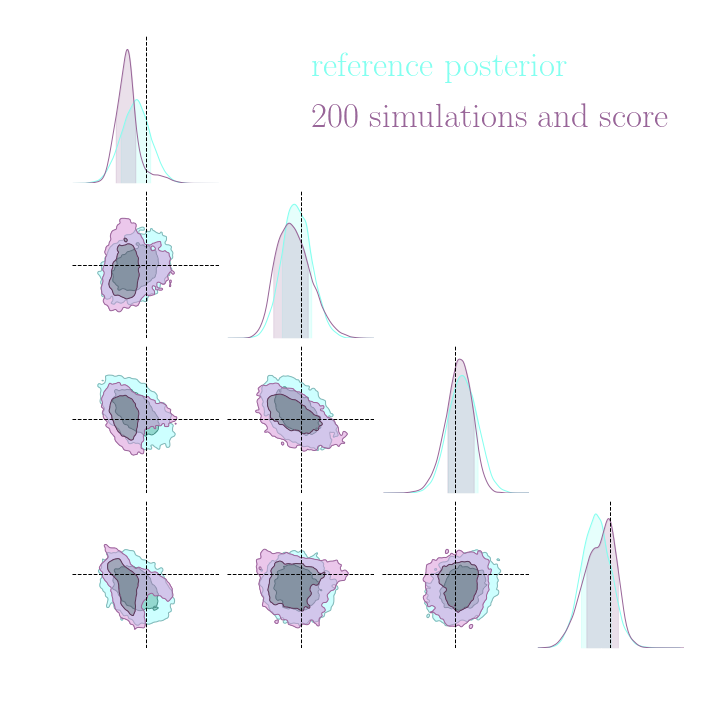
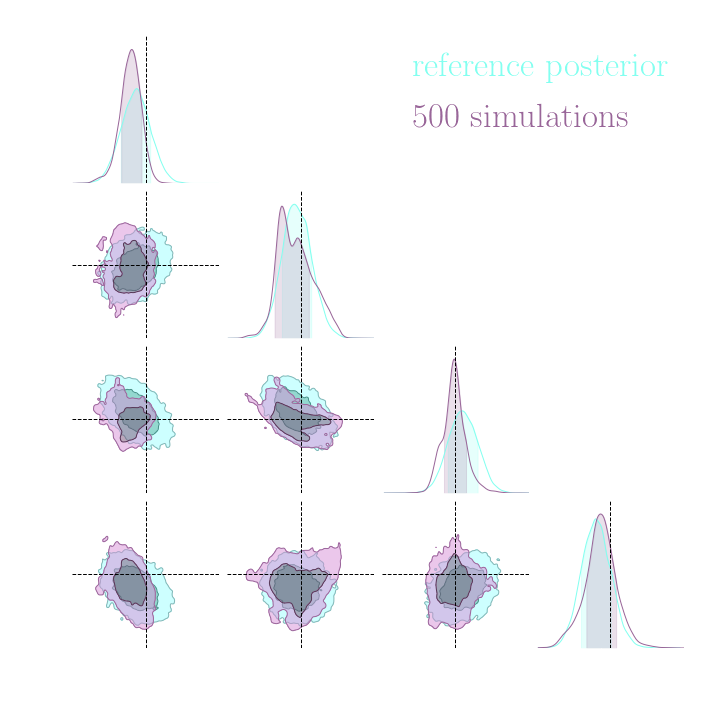
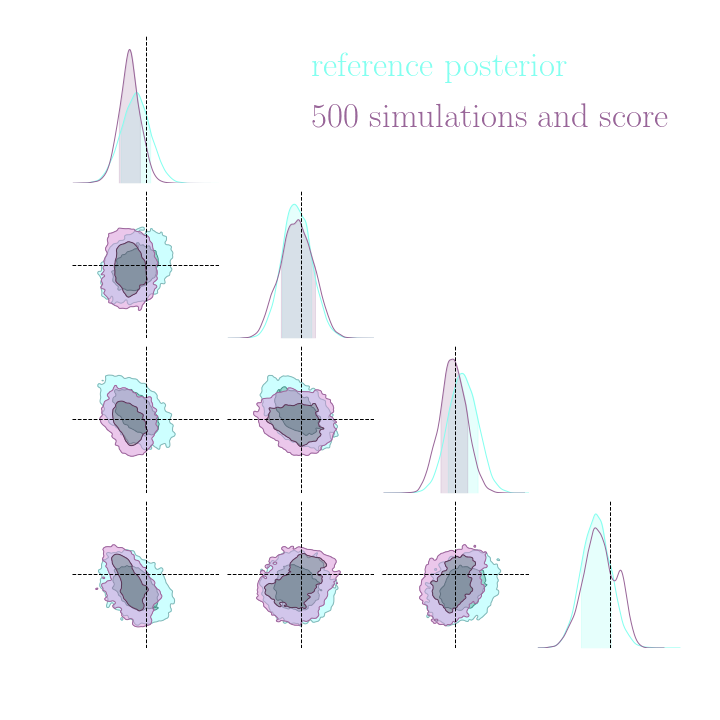
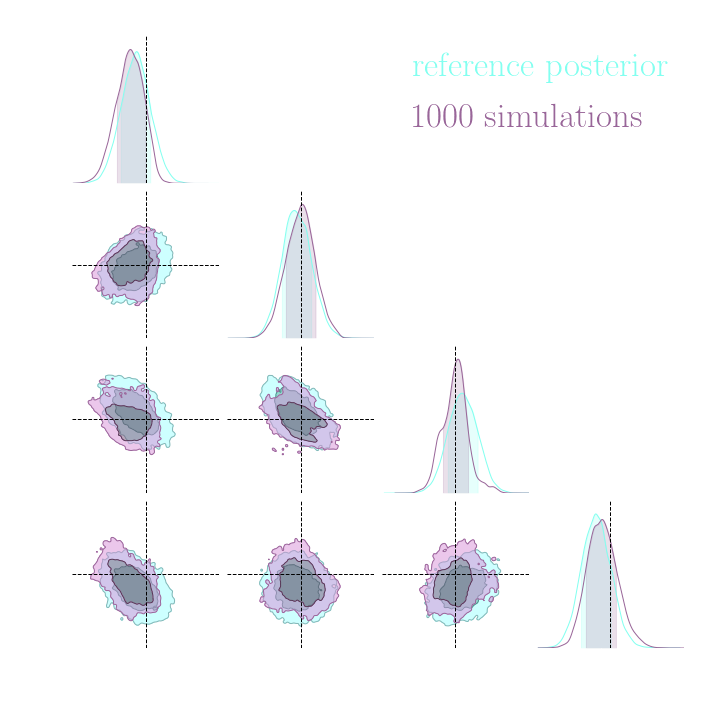
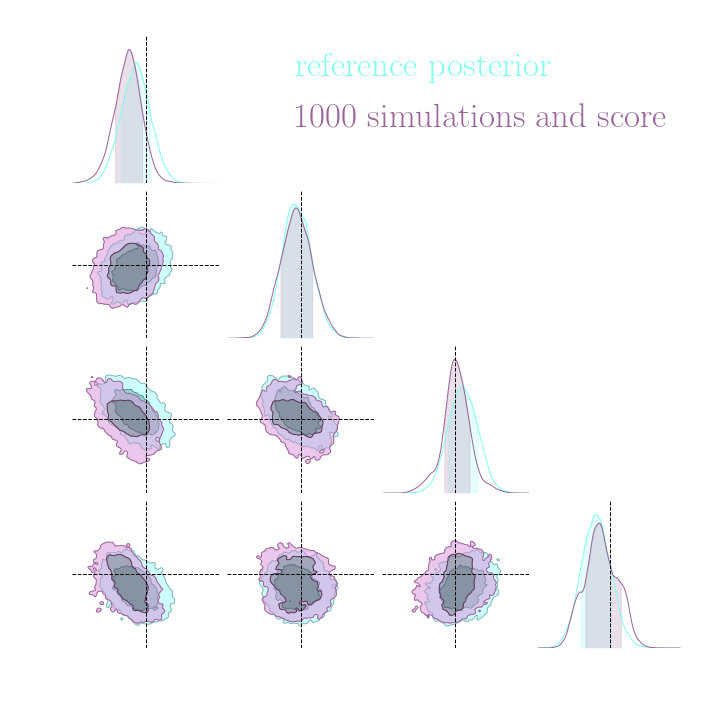
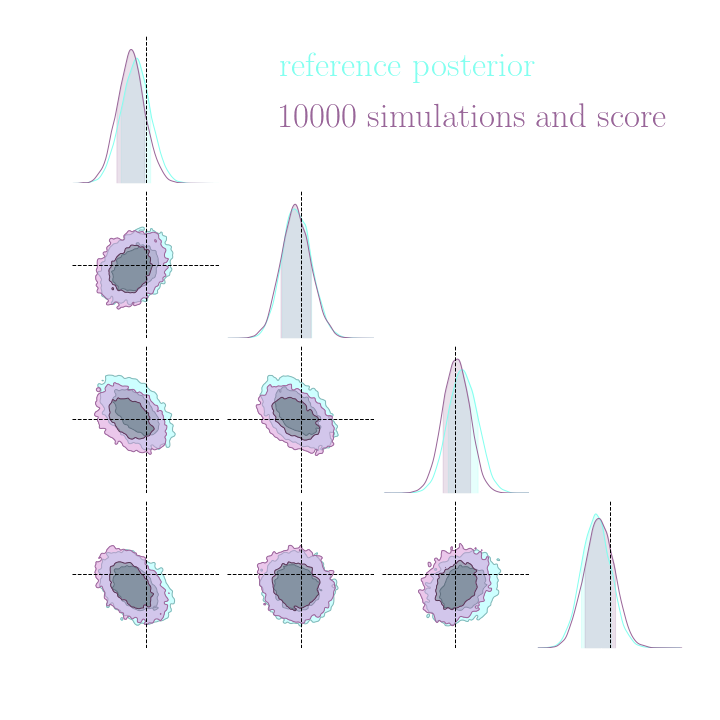
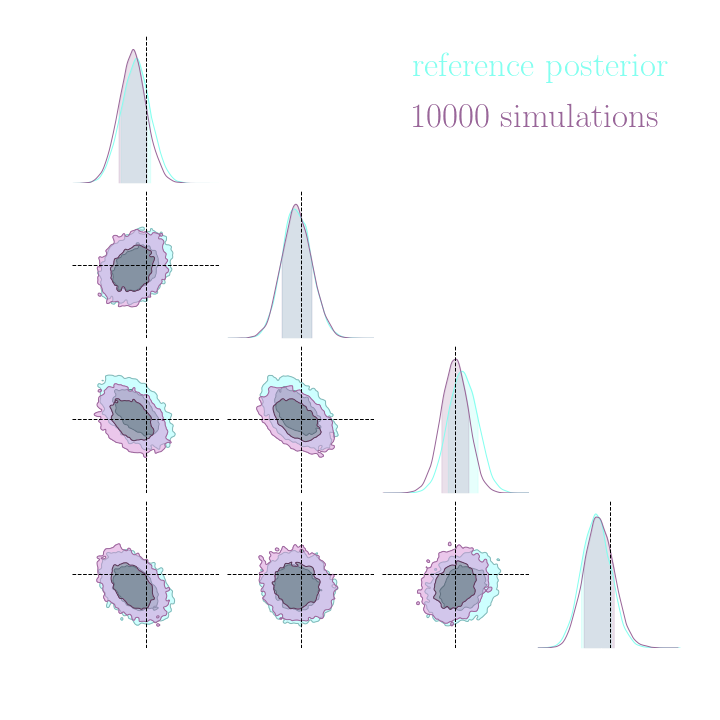
Without gradients

With gradients

 Posteriors on a toy model

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Simulation-Based Inference Benchmark for Weak Lensing Cosmology

Justine Zeghal, Denise Lanzieri, François Lanusse, Alexandre Boucaud, Gilles Louppe, Eric Aubourg, Adrian E. Bayer

and The LSST Dark Energy Science Collaboration (LSST DESC)

We developed a fast and differentiable (JAX) log-normal mass maps simulator.

DifferentiableUniverseInitiative/​sbi-lens

 For our benchmark: a Differentiable Mass Maps Simulator

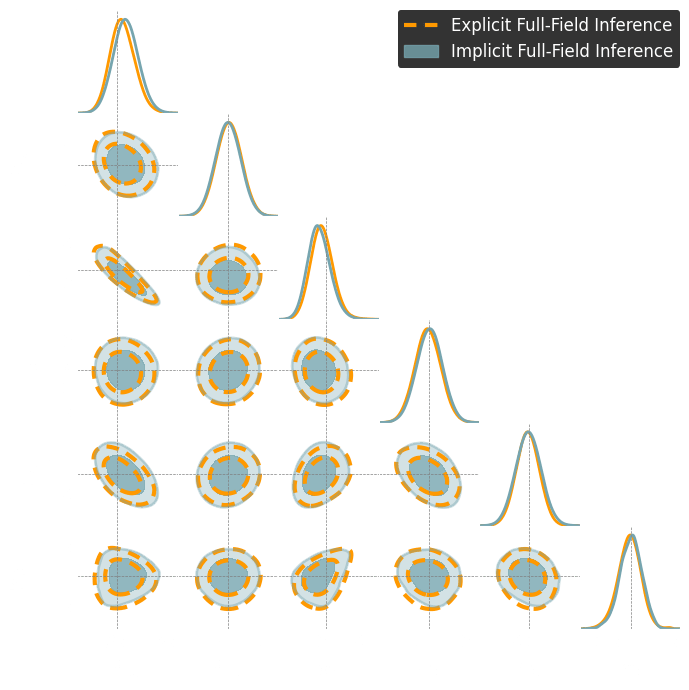
 Benchmark Results

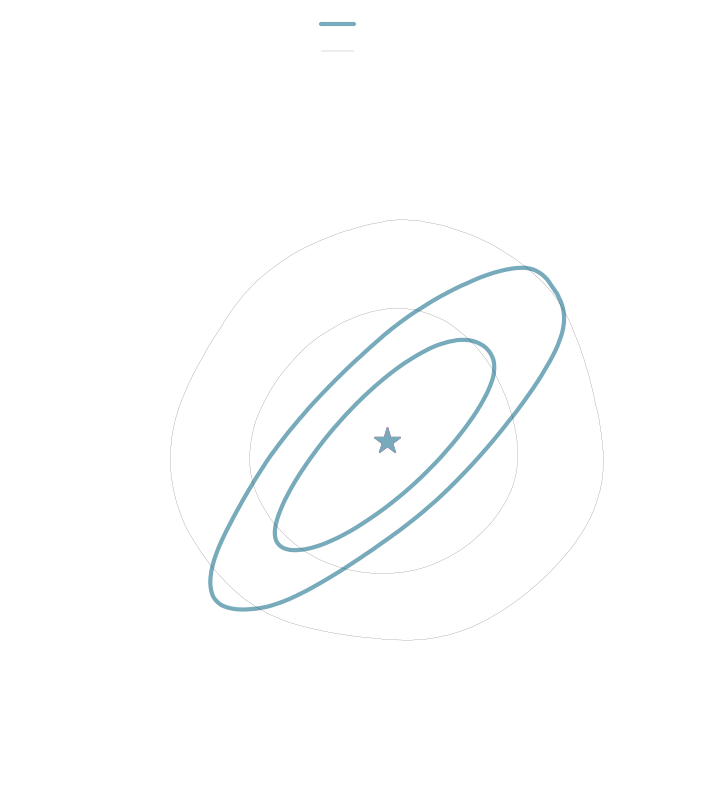
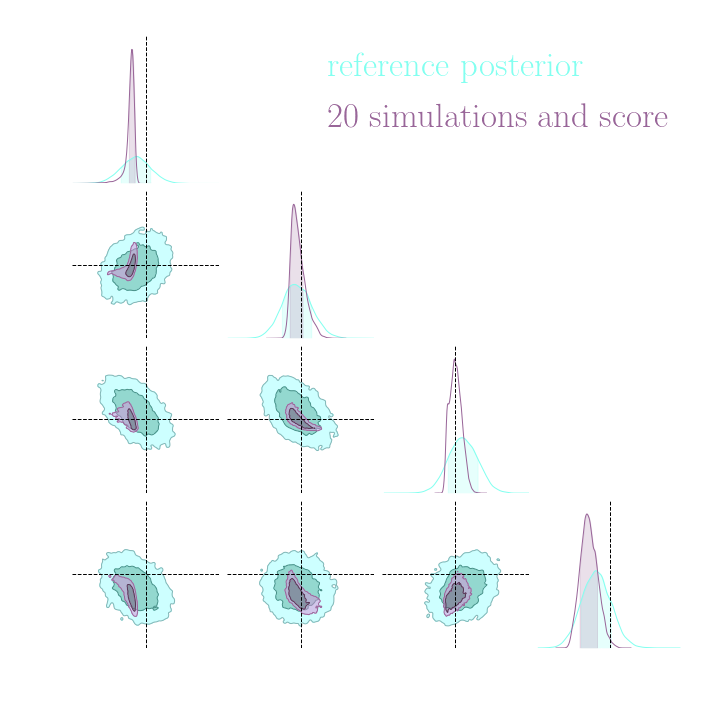
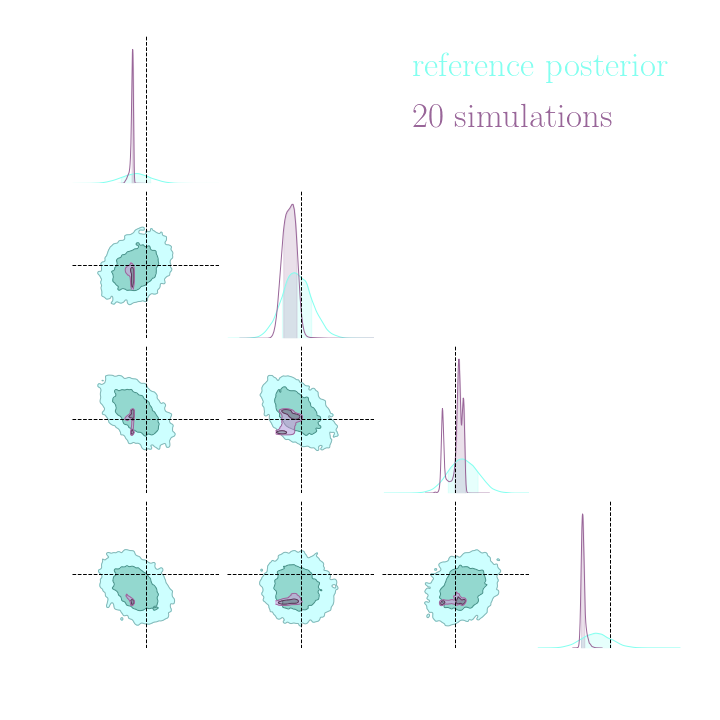
Both explicit and implicit inference yield the same posterior.

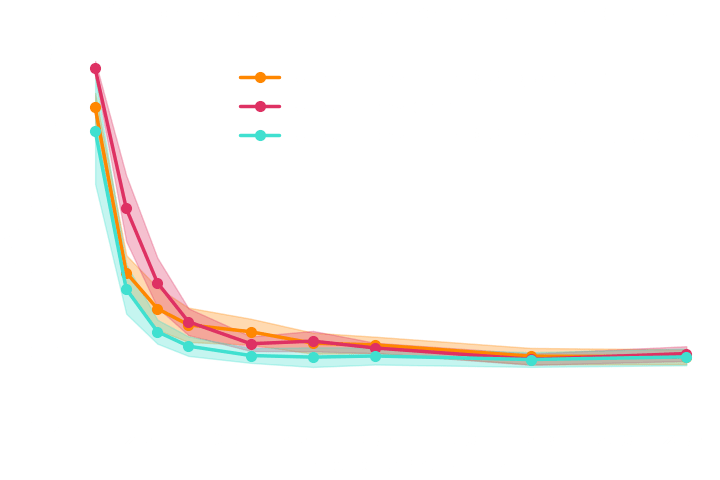
The gradients are too noisy to help reduce the number of simulations in implicit inference.

Implicit inference needs 10^3 simulations.

\displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(\theta, z |x) - \nabla_{\theta} \log p^{\phi}(\theta |x)\parallel_2^2 \right]

 Benchmark Results

Both explicit and implicit inference yield the same posterior.

Explicit inference needs 10^6 simulations.

The gradients are too noisy to help reduce the number of simulations in implicit inference.

Implicit inference needs 10^3 simulations.

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(x | \theta)\right) \right]
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(x, z |\theta) -{\nabla_{\theta} \log p^{\phi}(x|\theta )}\parallel_2^2 \right]

Training the NF with simulations and gradients:

Loss = 

  • Do gradients help implicit inference methods? 

- \mathbb{E}_{p(x, \theta)}\left[ \log\left(p^{\phi}(x | \theta)\right) \right]

Training the NF with simulations and gradients:

Loss = 

  • Do gradients help implicit inference methods? 

(\theta_i, x_i)_{i=1...N}
\nabla_{\theta} \log \hat{p}(x |\theta)
+ \: \lambda \: \displaystyle \mathbb{E}\left[ \parallel \nabla_{\theta} \log p(x, z |\theta) -{\nabla_{\theta} \log p^{\phi}(x|\theta )}\parallel_2^2 \right]

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Outline

Which full-field inference methods require the fewest simulations?

How to build sufficient statistics?

Can we perform implicit inference with fewer simulations?

How to generate more realistic simulations?

Bridging Simulators with Conditional Optimal Transport

Justine Zeghal, Benjamin Remy,  Yashar Hezaveh, François Lanusse,

Laurence Perreault-Levasseur

ICML co-located 2024 Workshop on Machine Learning for Astrophysics

 

A way to emulate is to learn the correction of a cheap simulation:

= \phi_1( \:\:\:\:\:\:\:\:\:)

→ OT Flow Matching enables to learn an Optimal Transport mapping between two random distributions.

Easier than learning the entire simulation evolution.

 We want:

  • the transformation to minimally  transform the simulation
  • learning a conditional transformation
  • work with unpaired dataset

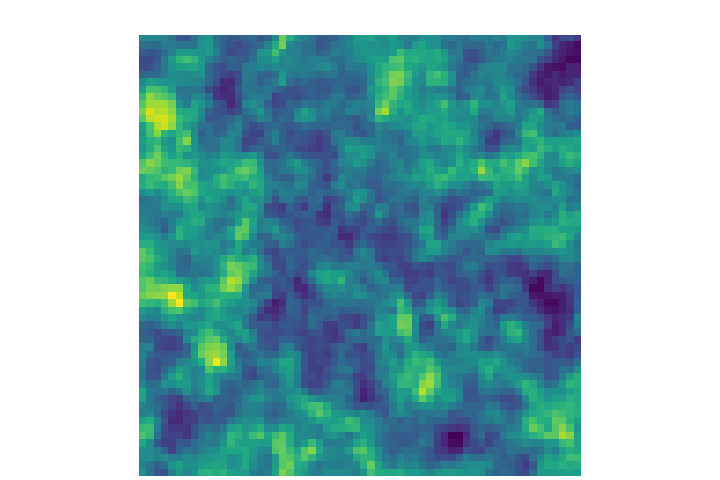
 Learning emulators to generate more simulations

With full-field inference, we are now only relying on simulations.

→ We need very realistic simulations.

 Flow Matching

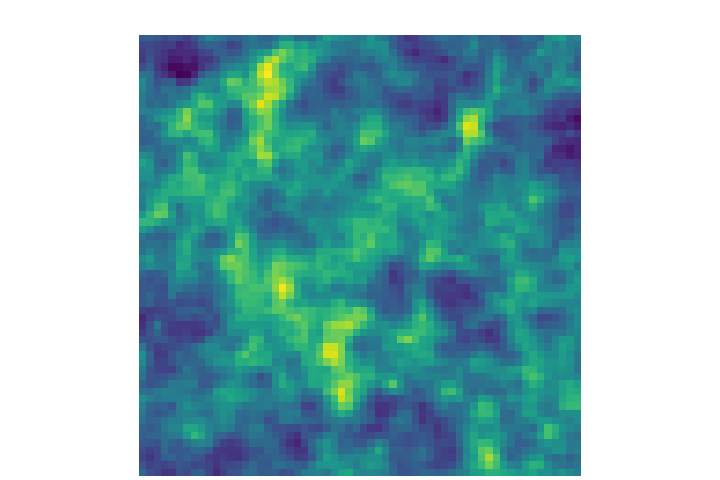
 Flow Matching

 Flow Matching

 Flow Matching

 Optimal Transport Flow Matching

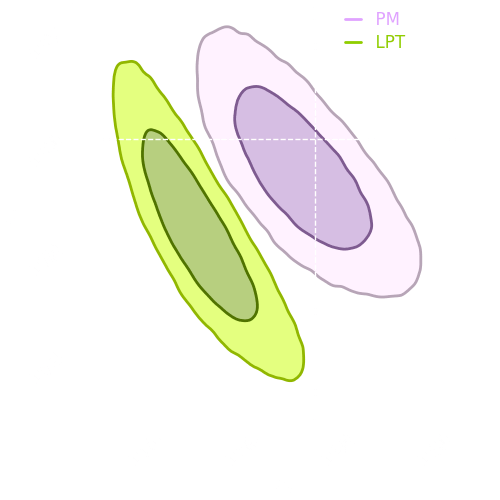
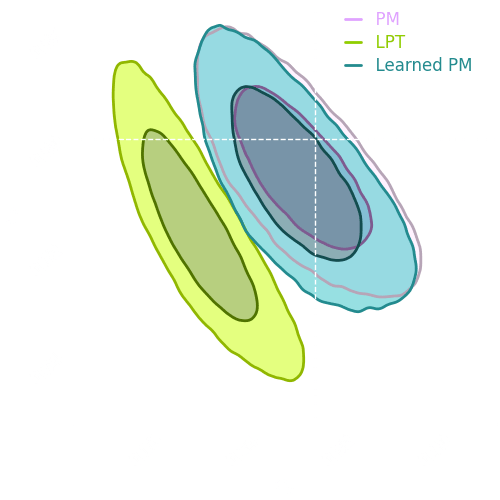
 Results

\theta

OT

\phi_1
\theta

LPT

PM

Experiment

→ Good emulation

at the pixel-level

→ We can perform both implicit and explicit inference

Conclusion

Which full-field inference methods require the fewest simulations?

Can we perform implicit inference with fewer simulations?

How to build emulators?

Gradients can be beneficial, depending on your simulation model. 

Explicit inference requires 100 times more simulations than implicit inference.

We can learn an optimal transport mapping.

How to build sufficient statistics?

Mutual Information Maximization

Thank you for your attention!

Summary statistics

t = f_{\varphi}(x)
p_{\Phi}(\theta | f_{\varphi}(x))
\theta

 Simulator

x