The Adoption of Blockchain-based Decentralized Exchanges 

Ruizhe Jia & Agostino Capponi 

Discussion by Katya Malinova

DeGroote School of Business

McMaster University

NFA 2021 (virtual)

 

  • asset class
  • common resource

Decentralized finance (DeFi): why exciting?

 

DeFi: provision of financial services without the necessary involvement of a traditional financial intermediary​
​

blockchain

Decentralized Exchanges

Idea:

  • use blockchain to exchange items
  • fully decentralized
    • no single controlling entity, nor location,
    • everything runs with smart contracts

 

How?

Decentralized Exchanges

Basic idea: (great!)

  • share the common resource:
    • pool the liquidity!
  • liq. providers:
    • deposit funds on both sides (e.g.,        and        ) to a liquidity pool
    • share gains & losses, don't compete with each other
  • liq. demanders:
    • trade against these funds
    • e.g., send        to the pool and get        from the pool

Question:

  • how to set the price/exchange rate?

 

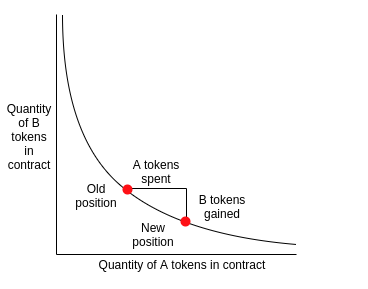
pricing mechanism:

  • \(A=\) contract balance of token A
  • \(B=\) contract balance of token B
  • \(k=\) invariance factor
  • key relation \(k=A\times B\ \) (constant product rule)
  • (Other \(F(A,B) = k\) possible)

Automated Market Maker

  • send \(\Delta_A=5\) of tokens A
  • \(\to\) receive \(\Delta_B\) of token B s.t.
  • \(k =10\times 10=(10+5)\times(10-\Delta_B)\)
  • \(\to\) get 3.33 tokens B  

Does/can this pricing function work?

10

10

15

6.67

  • This paper (see also Lehar & Parlour (2021) -- next in this session!):
    "Unbundle" liquidity provision & price discovery 
    • \(\to\) possible exploitable arbitrage opportunities = losses to liq. providers
      • \(\to\) "liquidity freezes" when exchange rates are too volatile
      • AMM best for "stable" pairs and/or those with high private value trading vol
      • a combo of linear & constant product pricing mitigates -- but doesn't eliminate -- this problem
         
  • Park (2021) (tomorrow at the NFA): Mechanical pricing + "tech details" \(\to\) possibilities for malicious behaviour (= losses/costs to investors)
    • The price computed using contract balances at settlement
      • \(\to\) opportunities for profitable "front-running" while in mempool (between "send the transaction in" and "settle")
      • proposes a different, pricing function, drawing on insights from microstructure

Possible issues? 

Very interesting paper: cleanly & clearly drills down to the economics of swap exchanges

  • participants incentives
  • \(\to\) sources, persistence (and consequences!) of arbitrage opportunities
  • mitigating these consequences ...
  • when/where the pricing works
  • effects on/externalities for the shared resource (gas fees)

 

 

Bottom line

  1. (Minor) too many "moving parts" & notation?
    ​
  2. Closer related to microstructure than the paper suggests ... 
    • liquidity (and lack of thereof) is HUGE in microstructure ... 
    • \(\to\) possible insights into DEX organization?
       
  3. Empirics:
    • Cool stylized facts! Support model's predictions, though not causal (?)
    • Trading volume: theory predictions are on "investor" volume (\(\to\)fraction of "noise/non-strategic trading") but doesn't your empirical volume measure include arbitrage trades?

 

Three sets of comments

  • Liquidity Providers (LP)
    • no pricing decisions

This paper's model                           vs                   "traditional" microstructure

  • Liquidity Providers (LP)
  • Investors
    • private values
    • incur "slippage"/price impact cost
    • + pay a preset % trading fee
  • Noise traders (?)
    • the bid-ask-spread cost
  • LP earns the bid-ask spread
  • noise trader loss = LP gain
  • LP unable to gain the "spread" (can't liquidate the new (better than original) position for free)
  • Arbitrageur: brings the contract reserves back, gains the "spread" but pays exactly that in gas fees \(\to\) earns zero profit
  • Miners (outside the model) earn the "spread"
  • LPs earn (twice) the trading fees
  • Liquidity Providers (LP)
    • earn trading fees, no gains from temp. "noise" price/position dislocations

This paper's model                           vs                   "traditional" microstructure

  • Exchange rate shock
    • the swap (reserve-quantity-based) exchange rate is stale \(\to\) any trade = loss to LP
  • Shock to the fundamental \(\to\) quotes become stale \(\to\) loss to LP
    • Adverse selection in limit order books b/c of public information:
      • Foucault (JFM 1999);  
      • Budish, Cramton, Shim (QJE 2015)
  • Equilibrium bid-ask spread increases in prob. of informed trading/prob. of shocks to fundamental
  • Lose more on info \(\to\) extract more from noise traders .... 
  • Severe adverse selection (large or very likely exchange rate shock)
  • \(\to\) fixed trading fees are insufficient to compensate LPs
  •  \(\to\) do not supply liquidity \(\to\) liq. freeze
  • Liquidity Providers (LP)
    • earn bid-ask spread
  • Is there ever a benefit for the LP to match the gas fee submitted by the arbitrageur in race to withdraw? (No for this model (?).)
  • Indirectly: alternate shapes of the pricing function [this paper & Park (2021)]
    • Affects noise trader incentives vs. arbitrageur incentives
    • \(\to\) possible to reduce losses to LPs

Mitigating liquidity freezes?

  • Involve an Oracle in pricing?
    • e.g., adjust contract reserves (\(\to\) swap exchange rate) based on external data?
    • (not that simple ....)
  • Any way for LPs to benefit directly from favourable contract reserve changes (i.e., better than "fair" swap exchange rates)  -- akin earning the bid-ask spread?
  • Variable trading fees? 
  • Role of the reserves size in the liquidity pools?

@katyamalinova

malinovk@mcmaster.ca

slides.com/kmalinova

https://sites.google.com/site/katyamalinova/