Optimal Fee Pricing
Roberto Riccó, Barbara Rindi, Duane J. Seppi
Discussion by Katya Malinova
DeGroote School of Business
McMaster University
EFA 2023 Annual Meeting
Amsterdam
Research question: in the title!
- Exchange trading fees
- Equilibrium?
- Socially optimal?
- Need for regulatory intervention?
- Key take-aways
- optimal fees (fees vs rebates) depend on investor valuation dispersion/gains from trade
- regulatory fee caps when exchange can extract rents
Building on Yong, Yao, Ye (2018): rebates \(\to\) finer tick size
Sophie: V = 20.0325
has the asset
Katya: V = 20.0375
price = 20.04
price = 20.03
Gains from trade \(\checkmark\)
but: the grid is too wide
Trade @p=20.03,
fee of 0.005 on Katya, rebate 0.005 to Sophie
Trade @p=20.04
fee of 0.005 on Sophie, rebate 0.005 cent to Katya
As if trade @20.035
This paper: investor valuations play a role!
Sophie: V = 20.0325
has the asset
Roberto: V = 25.0375
500 price levels between 20.04 and 25.03 to trade at
No need to rebate anybody for a trade to occur
Trade occurs even for large trading fees
\(\to\) exchange rent extraction!
2-period limit order book, monopolistic exchange
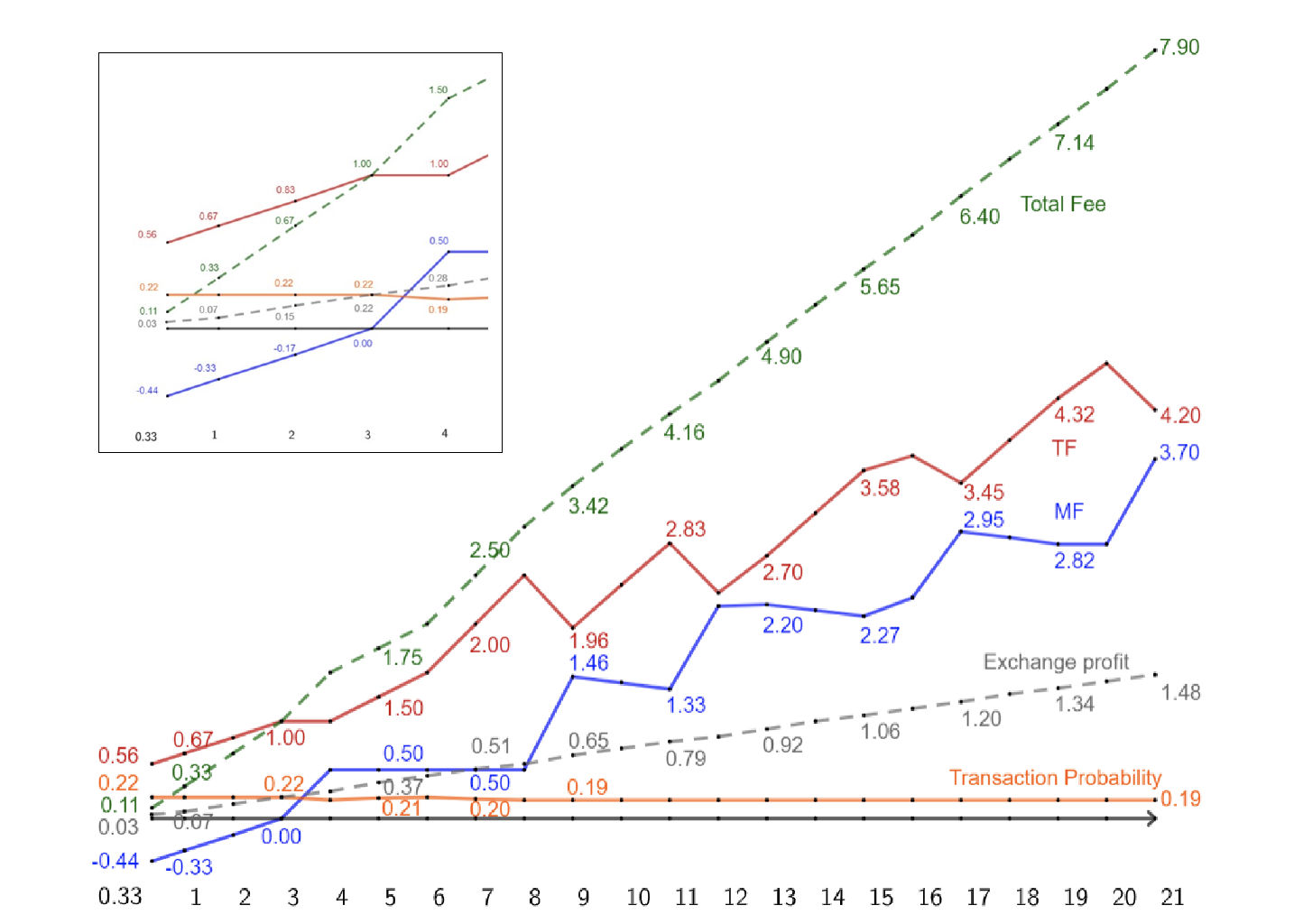
Maker + taker = total exchange fee
Taker fee
Maker fee
Exchange profit
Range of investor valuations
Rebates only for small ranges of valuations = low gains from trade
transaction probability
Fees oscillate with changes in valuation ranges:
- want makers to post the highest bid
- want more takers to trade when the posted bid worsens by a tick
2-period limit order book, social planner
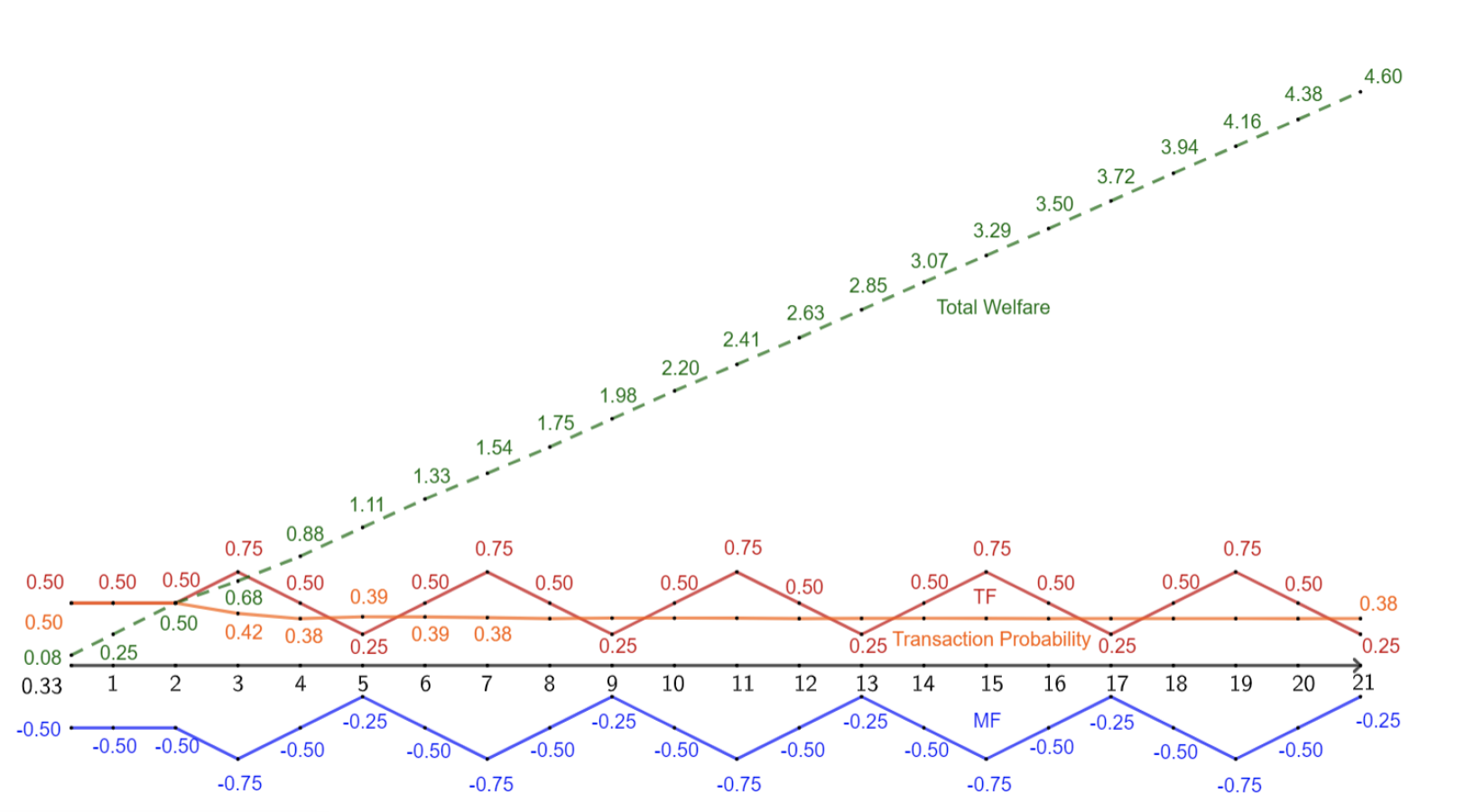
Welfare
Taker fee
Maker fee
Set the total exchange fee to 0
Questions:
- Why "cap the access fee" and not "cap the total" as the regulatory intervention?
- If the total fee can be capped, would the rebates re-emerge for valuations?
- Cheap shot: exchange competition?
2-period limit order book: Questions and Comments
- Practical implications of "oscillating" fees?
- challenging to implement even if valuations are proxied for
- Restrictions and limitations of 2 periods and/or sequential entry and/or no intermediation?
- One maker & one taker out of the set
- Fees must incentivize trading among these two
- Back to the example
- Maker: Sophie V = 20.3025, has the asset
- Takers: Katya V = 20.3075 and Roberto V = 25.3075
- Want Sophie to trade with Roberto!
- With >2 periods, may want the fees such that Katya does NOT trade?
- One maker & one taker out of the set
Side comment 1: model solved for limit buys (?), do the values of the optimal fees depend on this?
Side comment 2: authors interpret valuations range = "trading demand"
To me: large demand = lots of orders/frequent arrival
3-period model, monopolistic exchange:
barely any oscillations (?)
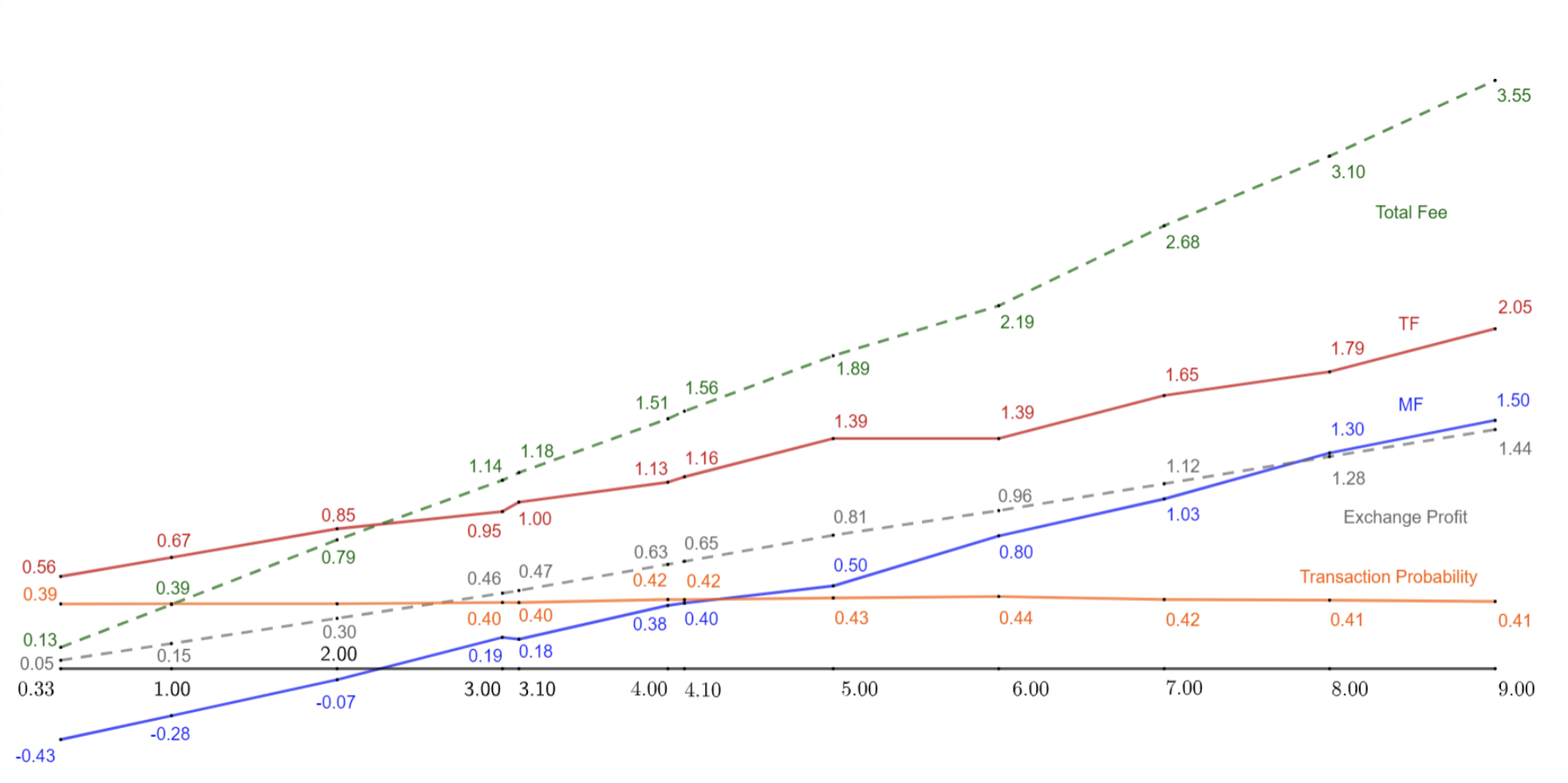
Question/suggestion:
- Do multiple periods "smooth" the fees?
- If so, focus on >2 periods?
Optimal Fees = huge task
- Yong, Yao, Ye (2018):
- rebates help resolve frictions re: tick size
- But re: optimal:
- is the tick size the only friction?
- other reasons for rebates?
- market segmentation?
- exchange competition?
- optimal fees vs. optimal market structure?
A step back: why trading fees & "rebates"?
Traditional approach
- Traders:
- buyers & sellers
An alternate view
- Traders:
- liquidity suppliers & liquidity demanders
-
Exchange = service provider
- facilitates trading
- collects trading fees
- If anybody gets paid
- \(\to\) "rebate"
-
Service providers = liquidity suppliers
- must be compensated
- inventory costs, adverse selection costs
- must be compensated
- \(\to\) Liquidity demanders compensate liquidity suppliers
- bid-ask spread
- fees (aka "maker rebates")
A step back: why trading fees & rebates?
An alternate view
- Traders:
- liquidity suppliers & liquidity demanders
-
Service providers = liquidity suppliers
- must be compensated
- inventory costs, adverse selection costs
- must be compensated
- \(\to\) Liquidity demanders compensate liquidity suppliers
- bid-ask spread
- fees
DeFi trading (AMM):
- asset owners = liquidity suppliers
- no tick size
- no bid-ask spread
- \(\to\)liquidity suppliers must be compensated through fees
- Malinova&Park (2023)
- propose AMM implementation approach in equities
- \(\to\) estimate savings of $-billions in trading costs ...
One big friction = exchange?

Summary
-
Excellent paper!
-
Cool new -- yet, close enough to the workhorse classic -- methodology!
-
Read it, use it, cite it!
@katyamalinova
malinovk@mcmaster.ca

slides.com/kmalinova
https://sites.google.com/site/katyamalinova/