Learning from DeFi: Would Automated
Market Makers Improve Equity Trading?
Katya Malinova and Andreas Park
Warwick Business School Gillmore Centre Conference
DeFi & Digital Currencies
The Shard. London 27 & 28 October 2023

Preliminaries & Some Motivation
- Blockchain: borderless general purpose value and resource management tool
Basic Idea
- DeFi: financial applications that run on blockchains
- \(\Rightarrow\) brought new ideas and tools
- one new market institution: automated market makers
Decentralized trading using automated market makers (AMM)













Liquidity providers
Liquidity demander
Liquidity Pool

AMM pricing is mechanical:
- determined by the amounts of deposits
- most common:
- constant product
- #USDC \(\times\) #ETH = const
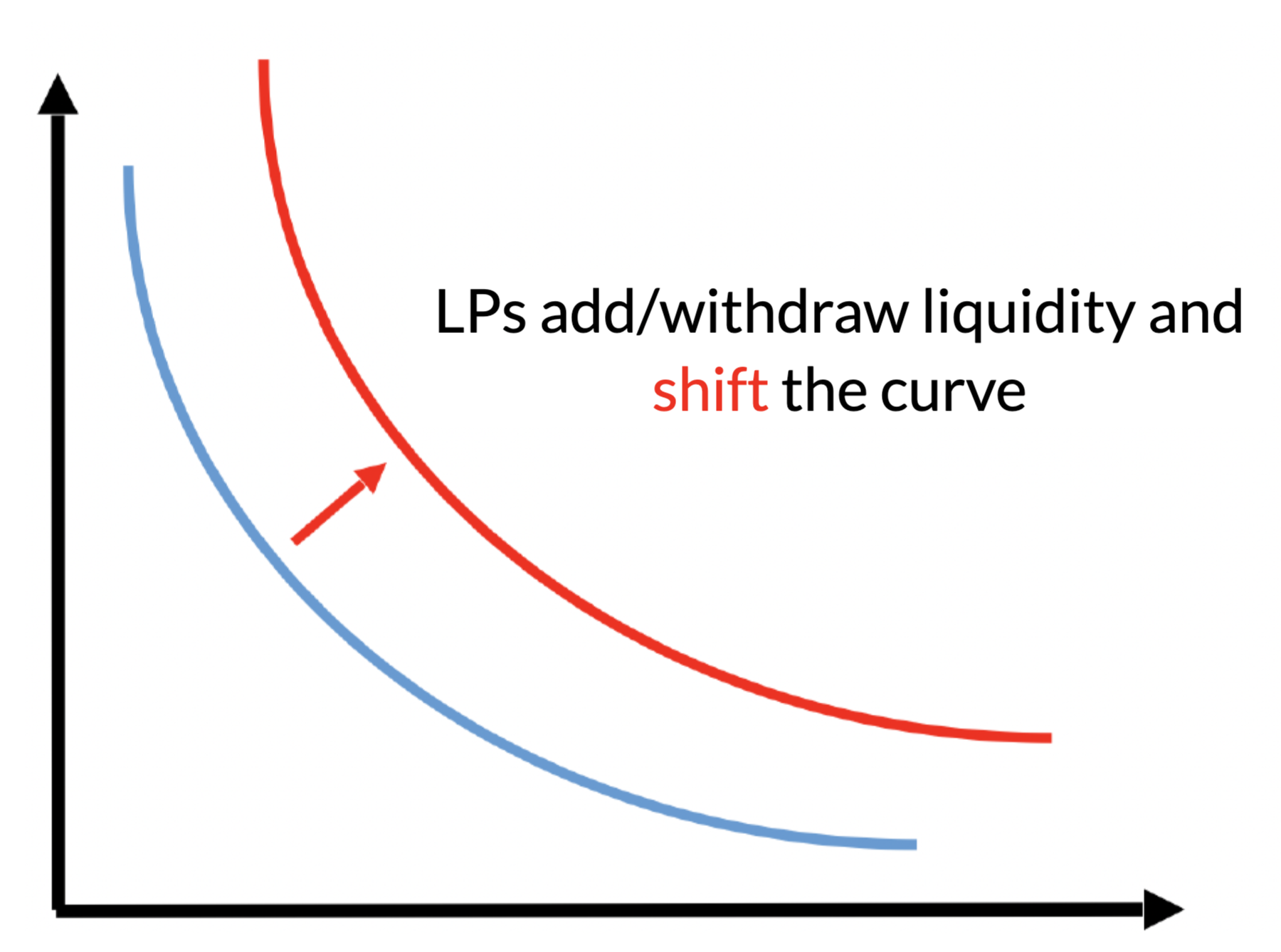
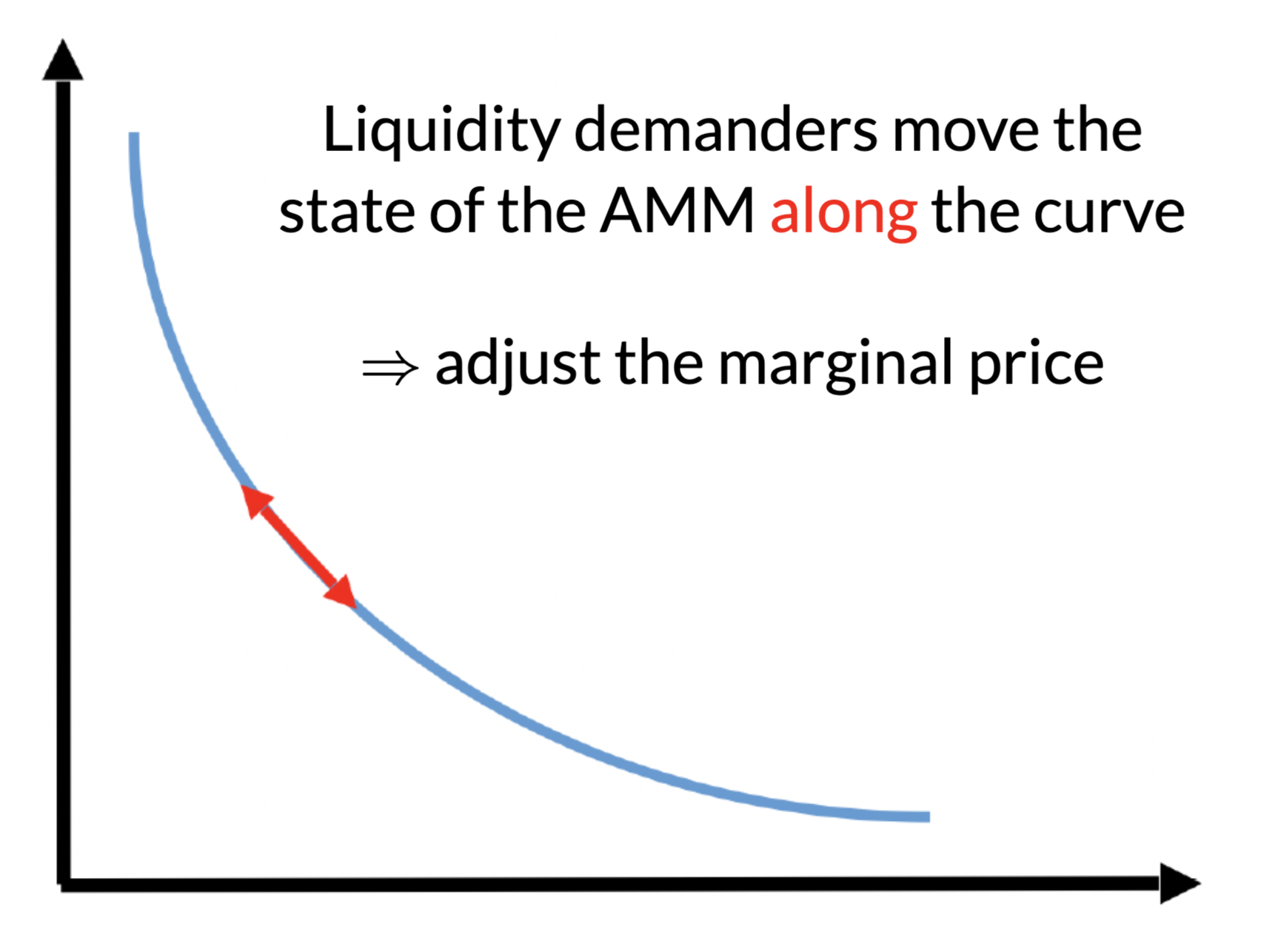
No effect on the marginal price
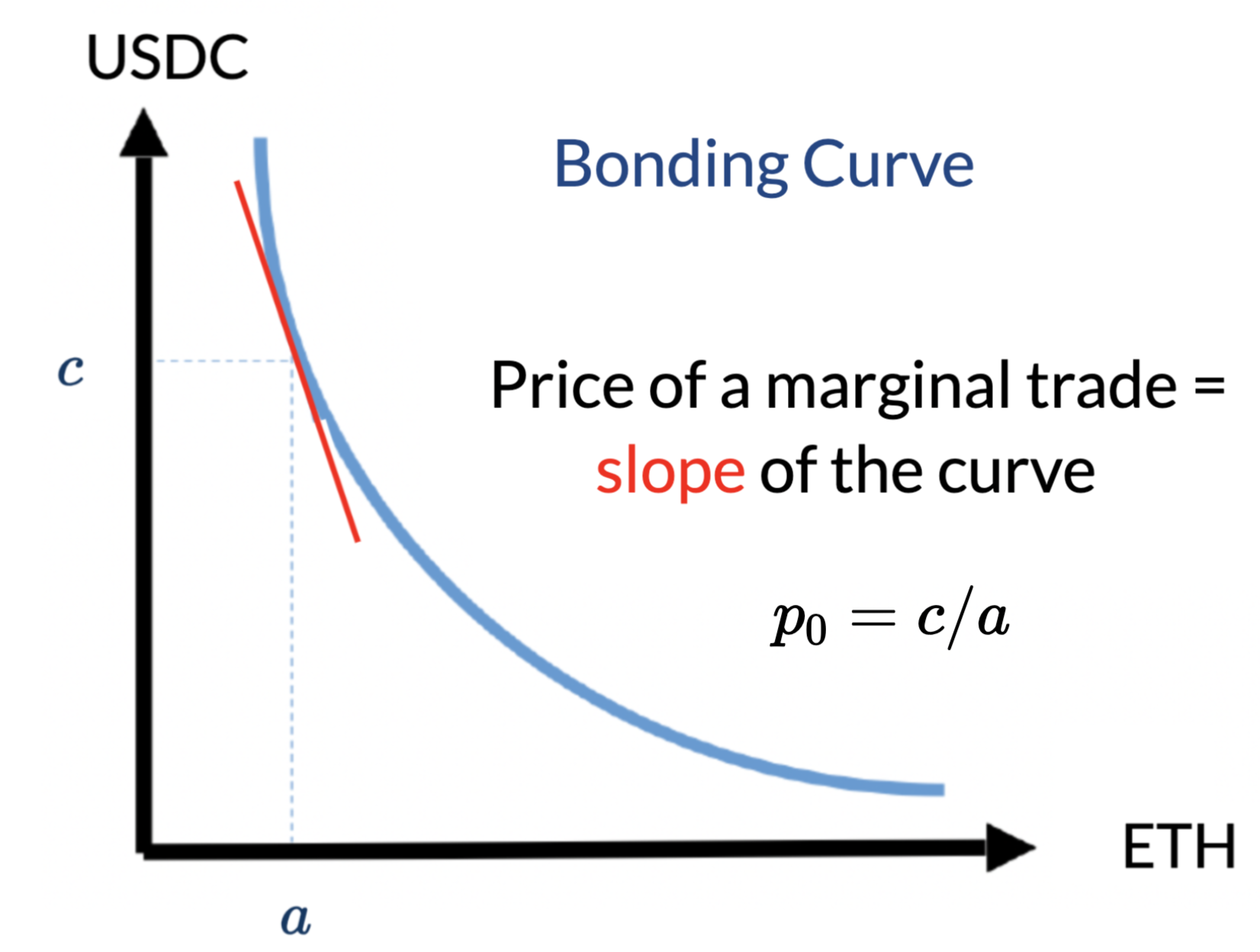
Key Components
- Our question:
- Can an economically viable AMM be designed for current equity markets?
- Would such an AMM improve current markets?
- Pooling of liquidity!
- Liquidity providers:
- pro-rated
- trading fee income
- risk
- use assets that they own to earn passive (fee) income
- retain exposure to the asset
- pro-rated
- Liquidity demanders:
- predictable price
- continuous trading
- ample liquidity
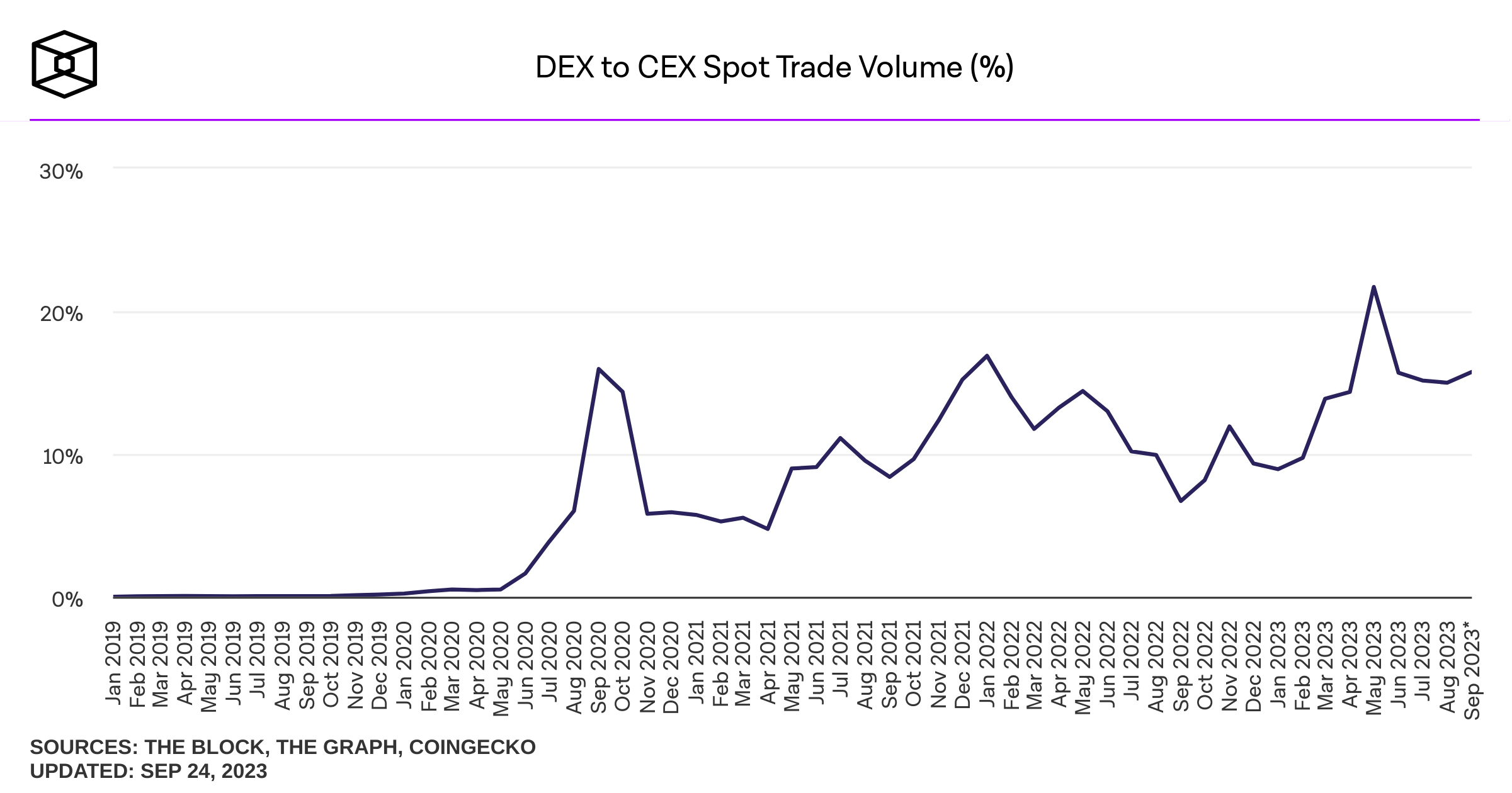
Liquidity Supply and Demand in an Automated Market Maker
Liquidity providers: positional losses
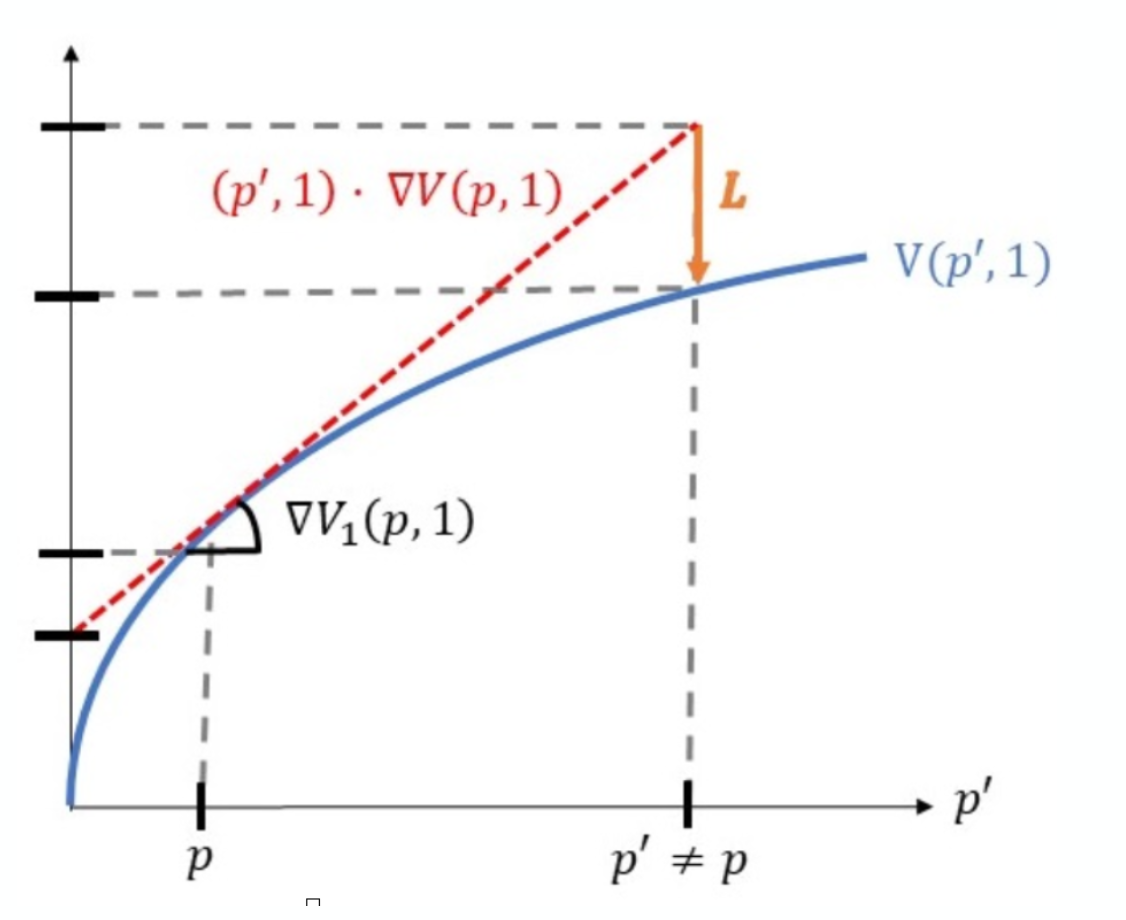
- Deposit asset & cash when the asset price is \(p\)
- Withdraw at price \(p'\ne p\)
Buy and hold
Provided liquidity
in the pool
- Why?
- adverse selection losses
- arbitrageurs trade to rebalance the pool
- \(\to\) always positional loss relative to a "buy-and-hold"
Returns to liquidity providers
- \(R\) = asset return
- F = trading fee
- V = balanced volume
- a = size of the liquidity pool
Similar to Lehar and Parlour (2023), Barbon & Ranaldo (2022).
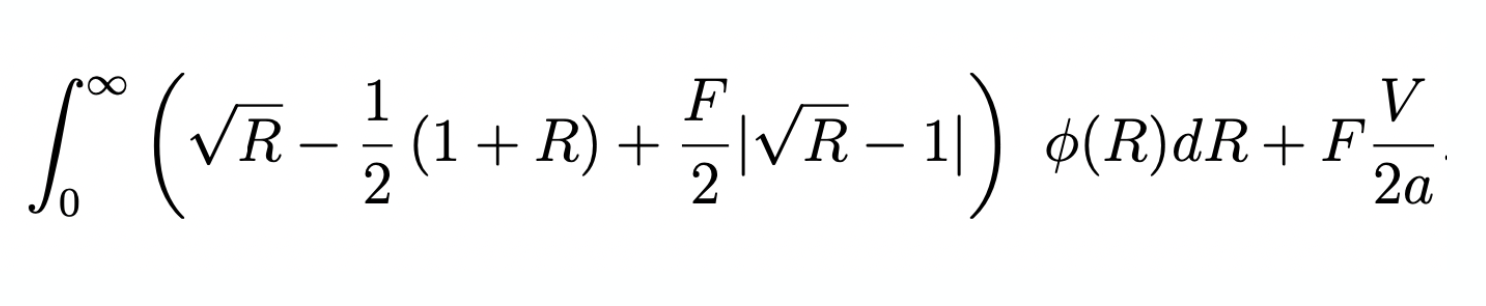
(incremental) adverse selection loss when the return is \(R\)
fees earned
on informed
fees earned
on balanced flow
for reference:
- If the asset price drops by 10% the incremental loss for liquidity providers is 13 basis points on their deposit
- \(\to\) total loss=-10.13%
- If the asset price rises by 10%, the liquidity provider gains 12 basis points less on the deposit
- \(\to\) total gain =9.88%
For fixed balanced volume \(V\) & fee \(F\):
- Larger pool size \(\to\) smaller shares of the fees
- \(\to \) LP expected return \(\searrow\) in pool size
-
Competitive liquidty provision:
- \(\to\) find the upper-bound on pool size above which LPs lose money
- we characterize this by \(\bar{\alpha}\) - fraction of the asset's market cap to be deposited to the pool
Liquidity Demander's Decision & (optimal) AMM Fees
- Better off with AMM relative to traditional market if
\[\text{AMM price impact} +\text{AMM fee} \le \text{bid-ask spread}.\]
- Two opposing forces when fee \(F\nearrow\)
- more liquidity provision
\(\to\) lower price impact - more fees to pay
- more liquidity provision
Result:
competitive liq provision\(\to\) there exists an optimal (min trading costs) fee \(>0\)
- \(\to\) derive closed form solution for competitive liquidity provision
- depends on return distribution, balanced volume, quantity demanded
Similar to Lehar&Parlour (2023) and Hasbrouck, Riviera, Saleh (2023)
What's next?
- Have:
- equilibrium choices for competitive liquidity provision
- fee that minimizes liquidity demander AMM costs (\(>0\))
- Next:
- Calibrate to stock markets
- AMM Feasible?
- AMM costs at the optimal fee < bid-ask spread?
How we think of the Implementation of an AMM for our Empirical Analysis
Approach: daily AMM deposits
- AMMs close overnight.
- Market: opening auction \(\to\) \(p_0\)
- Determine: optimal fee; submit liquidity \(a,c\)
at ratio \(p_0=c/a\) until break even \(\alpha=\overline{\alpha}\)
- Liquidity locked for day
- At EOD release deposits and fees
- Back to 1.
Background on Data
Special Consideration 1: What volume?
-
some volume may be intermediated
- with AMMs: no need for intermediation
- \(\to\) intermediated volume could disappear
- \(\to\) use volume/2
- Some caveats, e.g.
- arbitrageur volumes
- larger volume if AMM has lower trading costs
Special Consideration 2: What's \(q\) (the representative order size)?
- use average per day
- take long-run average + 2 std of daily averages
- (also avg \(\times 2\),\(\times 4\), depth)
All displayed data CRSP \(\cap\) WRDS
- CRSP for shares outstanding
- WRDS-computed statistics for
- quoted spreads (results similar for effective)
- volume
- open-to-close returns
- average trade sizes, VWAP
- Time horizon: 2014 - March 2022
- Exclude "tick pilot" period (Oct 2016-Oct 2018)
- All common stocks (not ETFs) (~7550).
- Explicitly not cutting by price or size
- All "boundless" numbers are winsorized at 99%.
Special Consideration 3:
Where to get returns and volume?
- Approach 1: "ad hoc"
- "one-day-back" look
- take yesterday's return and volume when deciding on liquidity provision in AMM
- Approach 2: estimate historical return distribution
AMMs based on historical returns
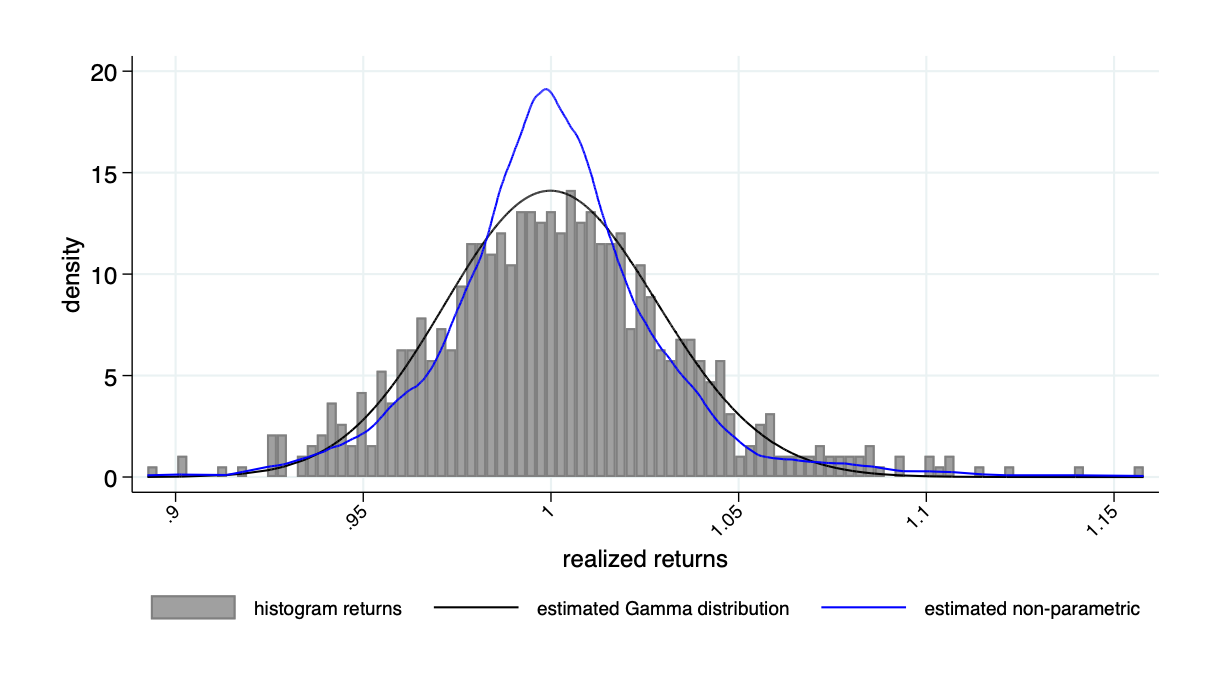
Return distribution example: Tesla
- average \(F^\pi=11\)bps
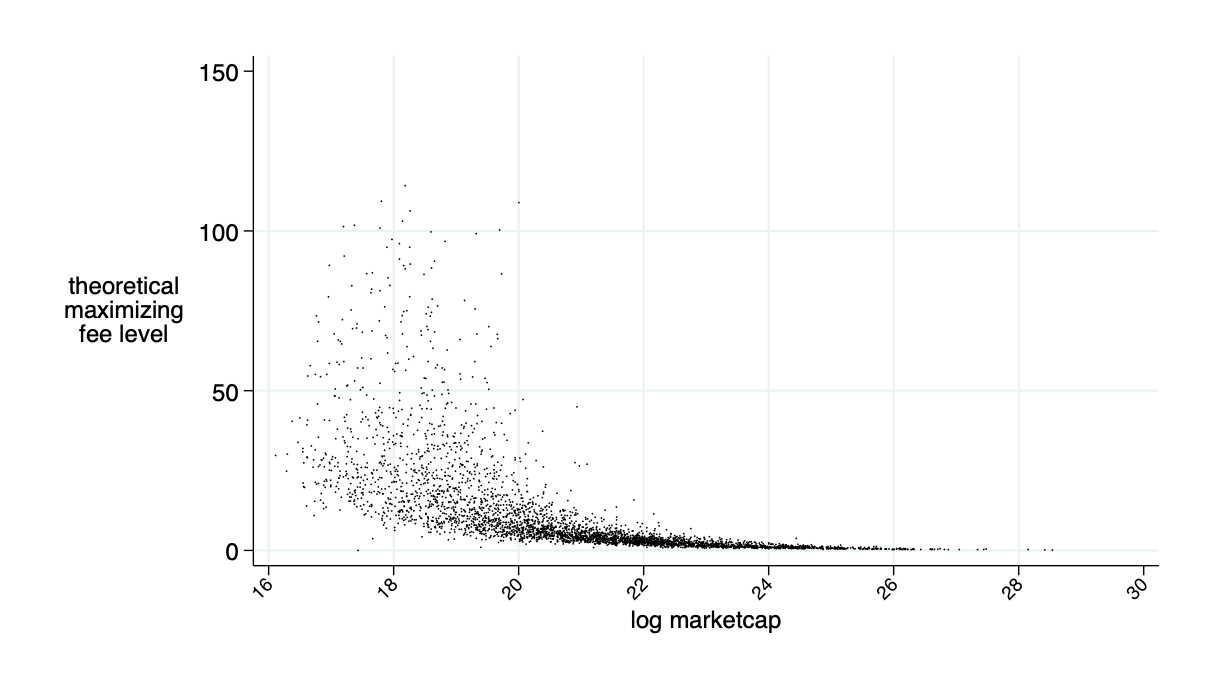
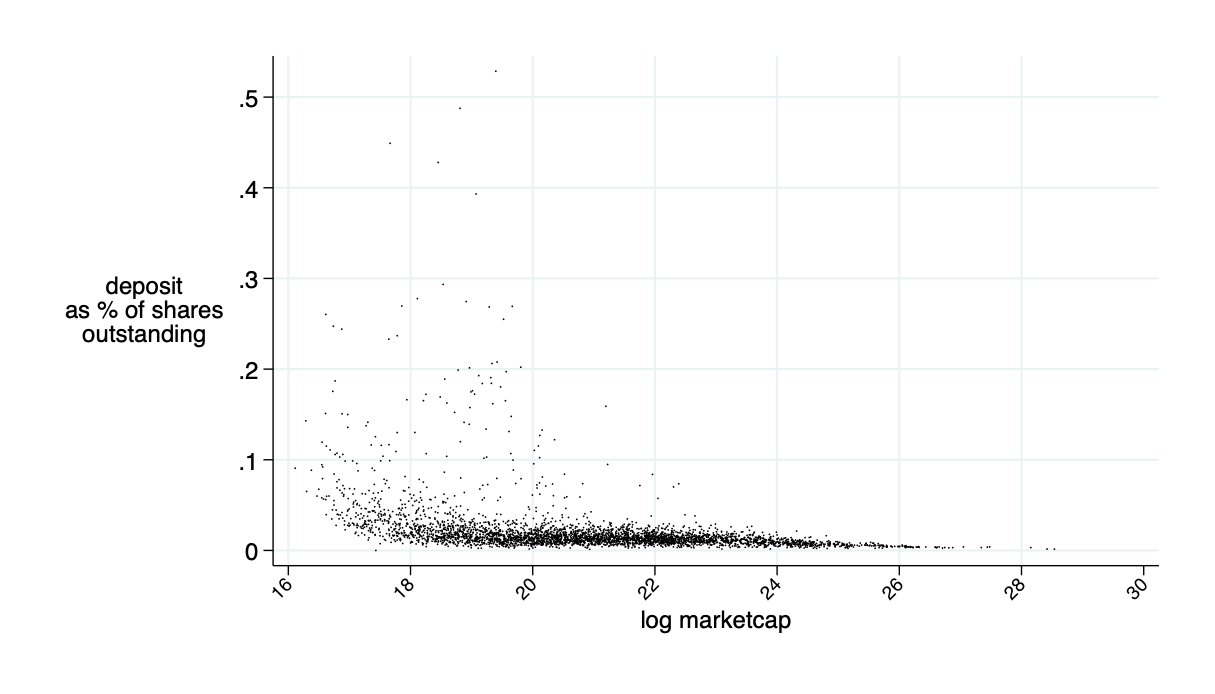
Average of the market cap to be deposited for competitive liquidity provision: \(\bar{\alpha}\approx 2\%\)
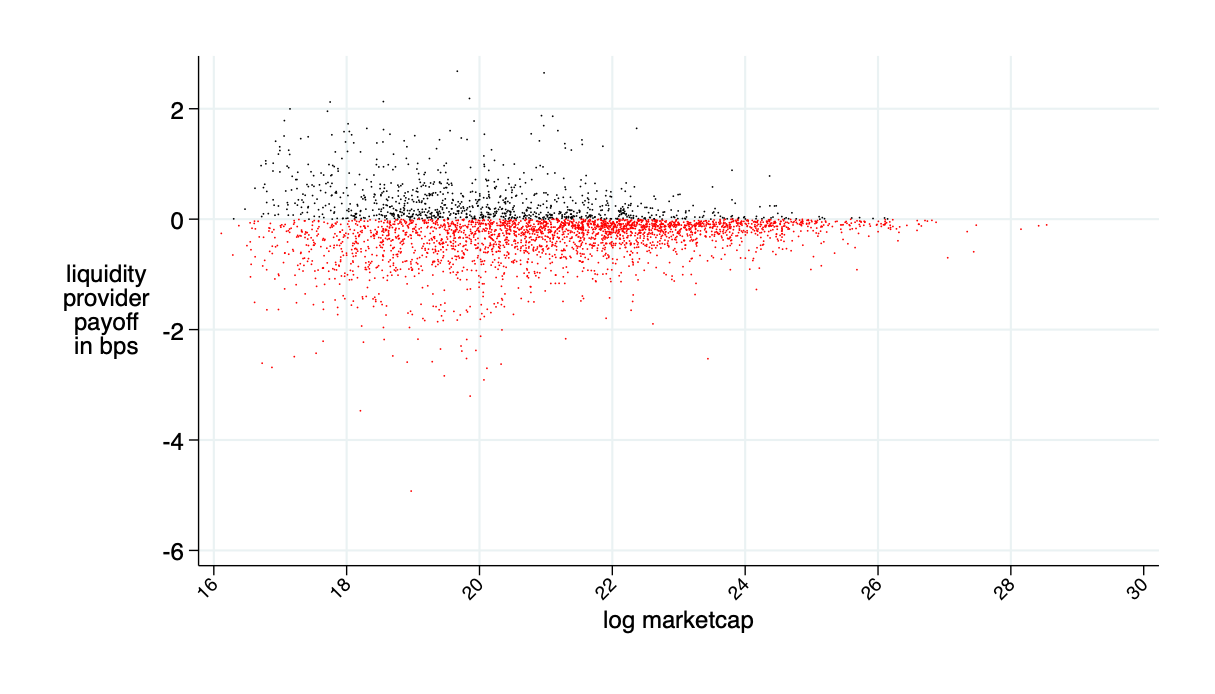
almost break even on average (average loss 0.2bps \(\approx0\))
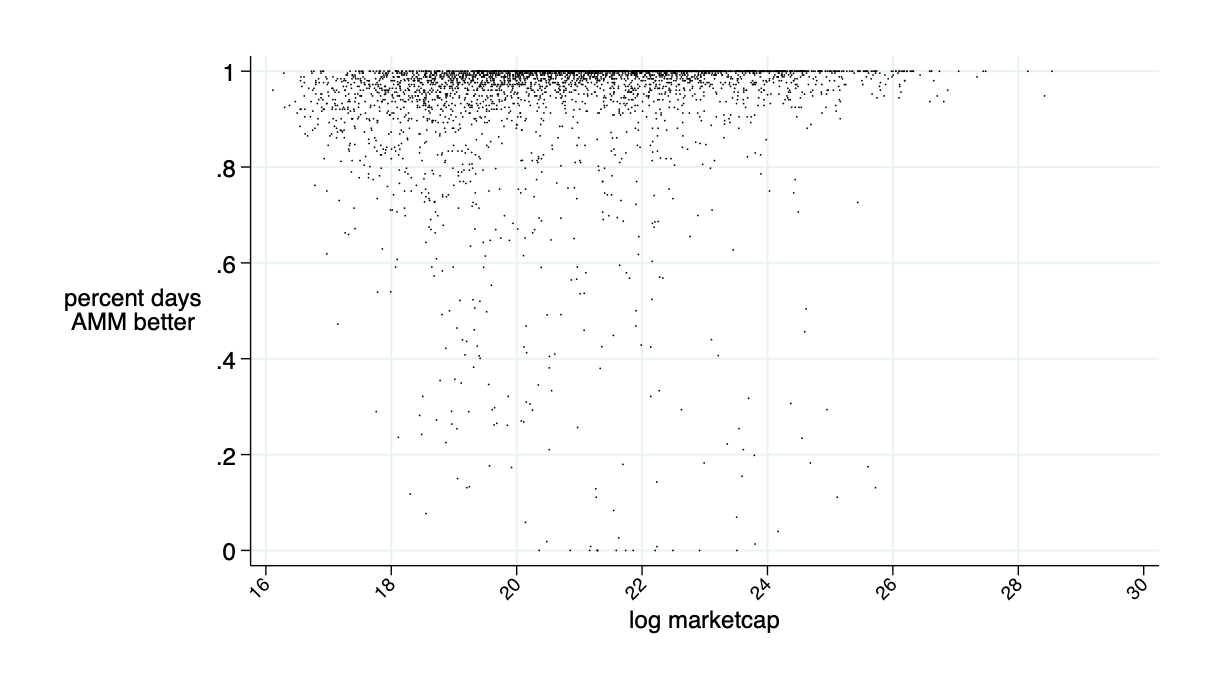
average: 94% of days AMM is cheaper than LOB for liq demanders
average savings: 16 bps
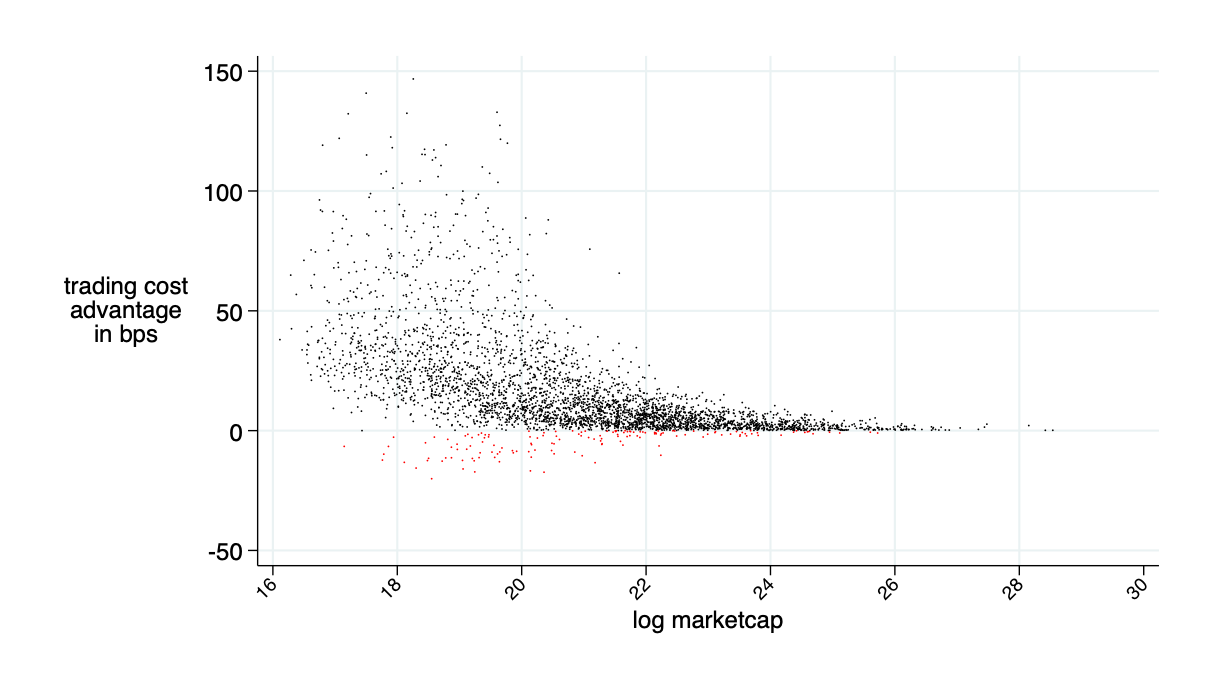
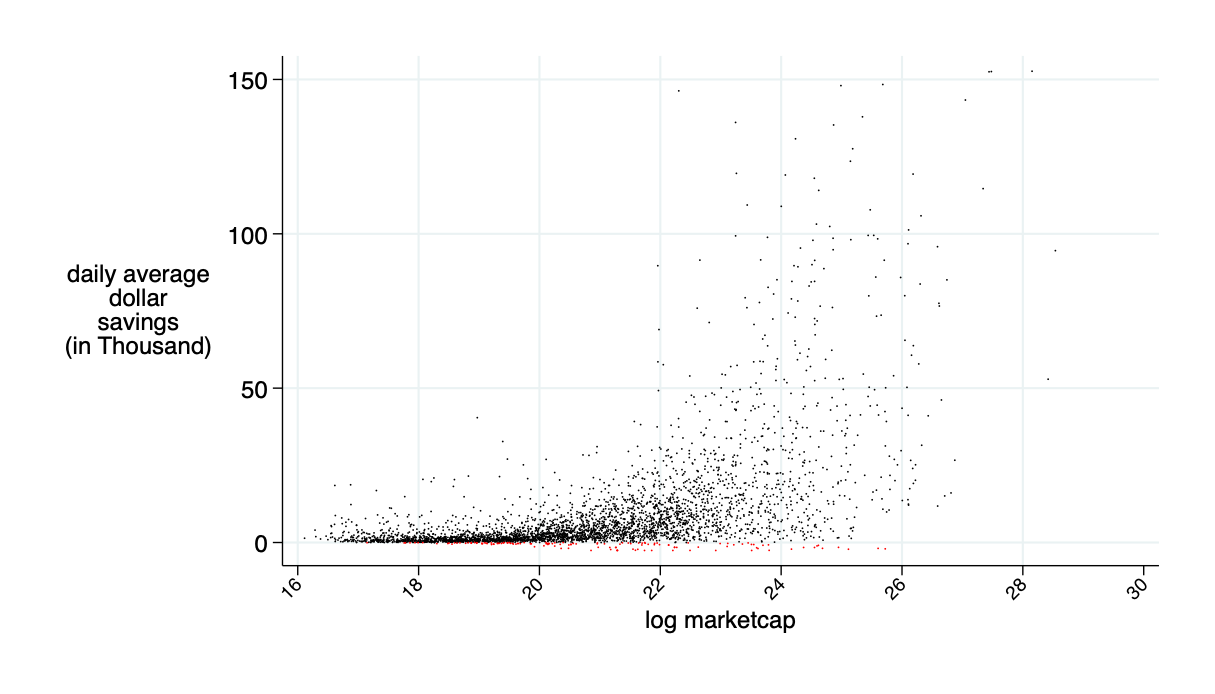
average daily: $9.5K
average annual saving: $2.4 million
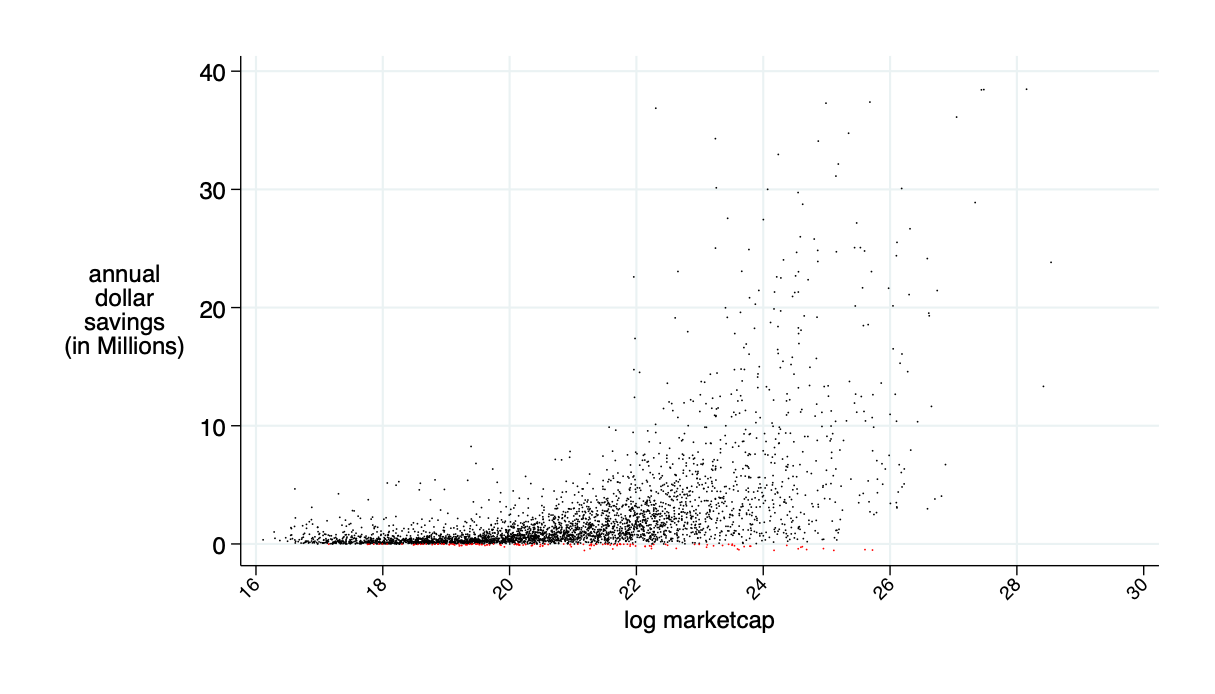
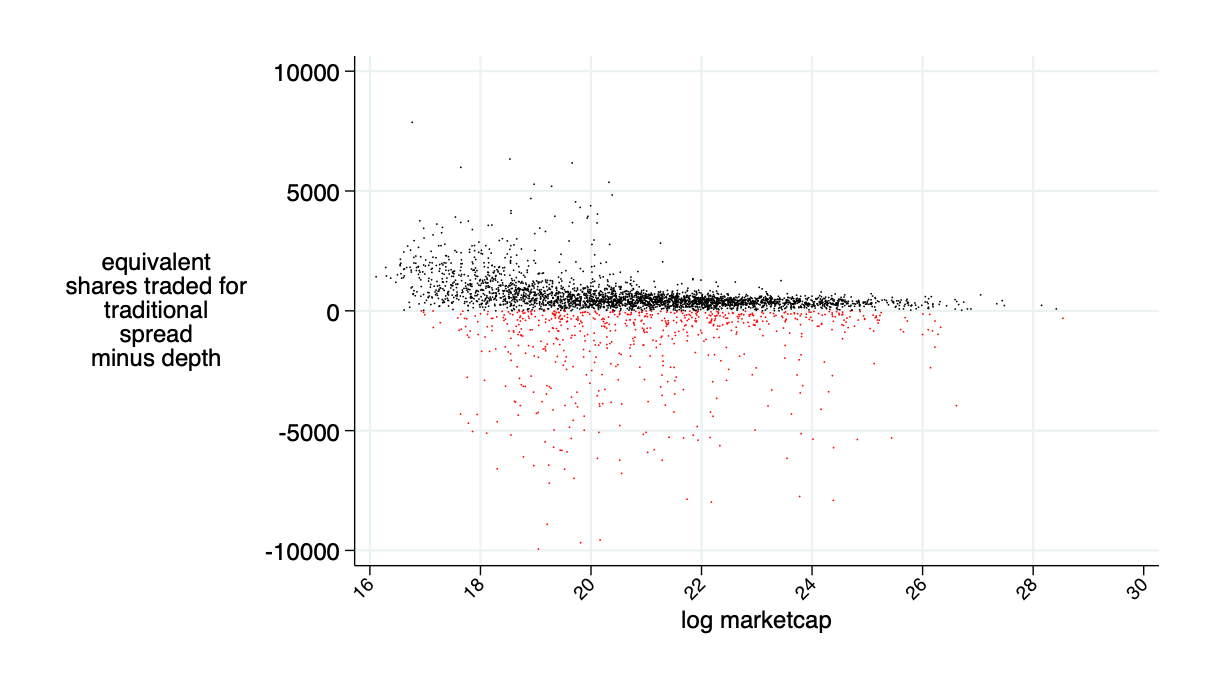
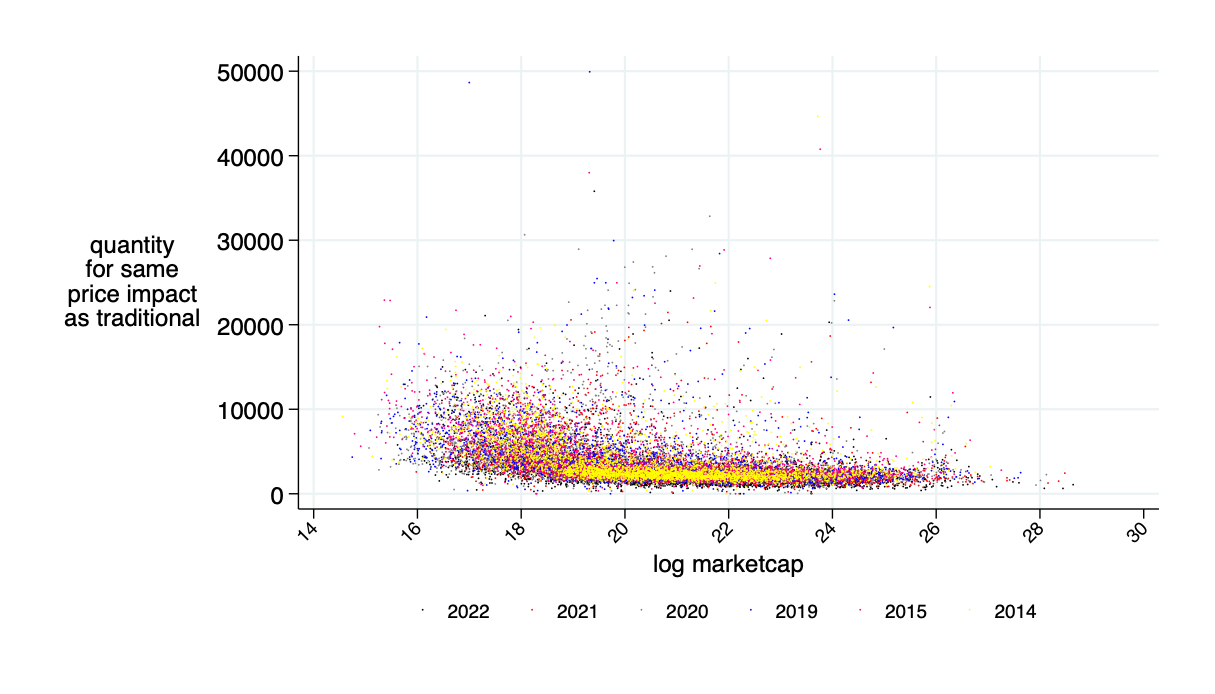
implied "excess depth" on AMM relative to the traditional market
Sidebar: Capital Requirement
Deposit Requirements
- Our approach: measure liquidity provision in % of market cap
- Share-based liquidity provision is not a problem: the shares are just sitting at brokerages.
- But: AMM requires an off-setting cash amount: \(c =a\cdot p(0)\).
- Cash is not free:
- at 6% annual rate, must pay 2bps per day.
- Would need to add to fees
- But: do we need "all that cash"?
- No.
- (hand-waving argument)
- 2nd gen AMMs have liquidity provision "bands": specify price range for which one supplies liquidity
- Here: specify range for \(R\in(\underline{R},\overline{R})\)
- Outside range: don't trade.
- Inside range: "full" liquidity with constant product formula.
- Implication: only need cash and shares to satisfy
in-range liquidity demand.
\(\Rightarrow \) Need about 5% of the value of the shares deposited -- not 100% -- to cover up to a 10% return decline
Summary
- AMMs do not require a blockchain - just a concept
- could be run in the existing world (though there are institutional and regulatory barriers)
- Our question:
- Can an economically viable AMM be designed for current equity markets?
- Would such an AMM improve current markets?
- Answers:
- Yes.
- Massively.
- Source of Savings:
- Liquidity providers \(\not=\) Citadel!
- \(\to\) no (overnight) inventory costs
- \(\to\) use idle capital
- \(\to\) + better risk sharing
@katyamalinova
malinovk@mcmaster.ca

slides.com/kmalinova
https://sites.google.com/site/katyamalinova/
Deposit Requirements
- For return \(R\), the following number of shares change hands: \[q=a\cdot(1-\sqrt{R^{-1}}).\]
- Fraction of share deposit used \[\frac{q}{a}=1-\sqrt{R^{-1}}.\]
- Fraction of cash used \[\frac{\Delta c ("R")}{c}=\frac{1-\sqrt{R^{-1}}}{\sqrt{R^{-1}}}.\]
- Example for \(R=.9\) (max allowed price drop \(=10\%\)) \[\frac{\Delta c ("R")}{c}=-5\%.\]
- \(\Rightarrow\) "real" cash requirements \(\not=\) deposits
\(\Rightarrow \) Need about 5% of the value of the shares deposited -- not 100% -- to cover up to a 10% return decline
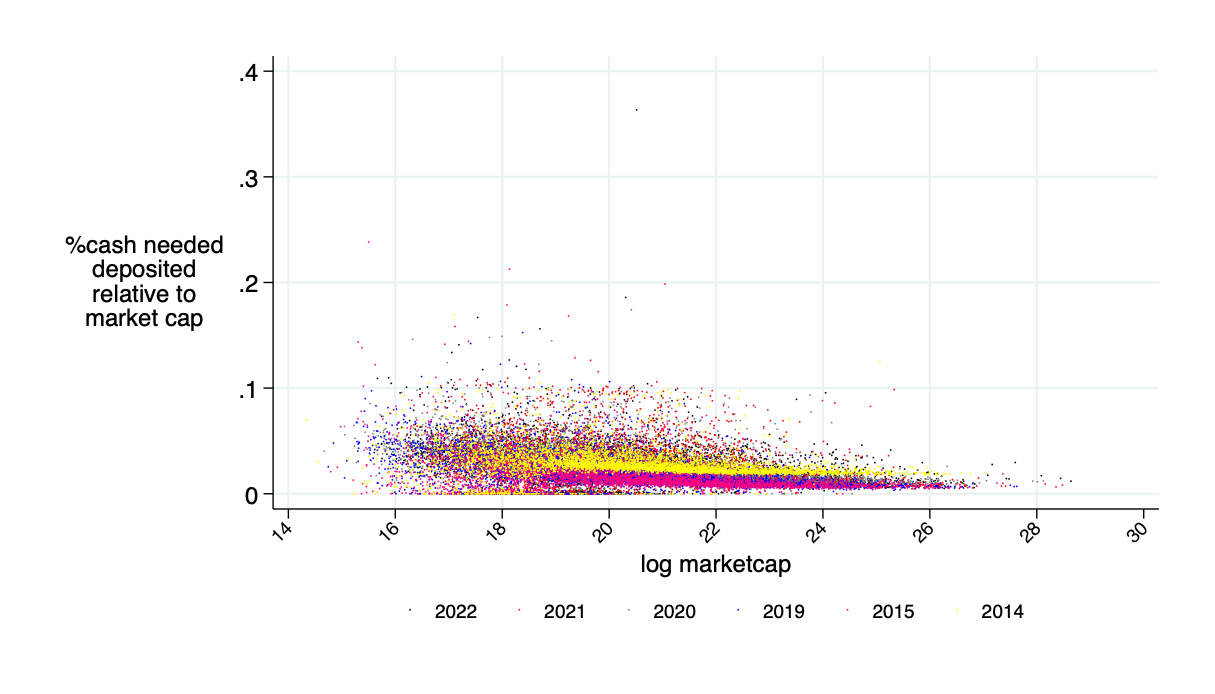
An alternative to -10% circuit breaker:
max cash needed based on long-run past average R \(-\) 2 std
Optimally Designed AMMs with
"ad hoc" one-day backward look
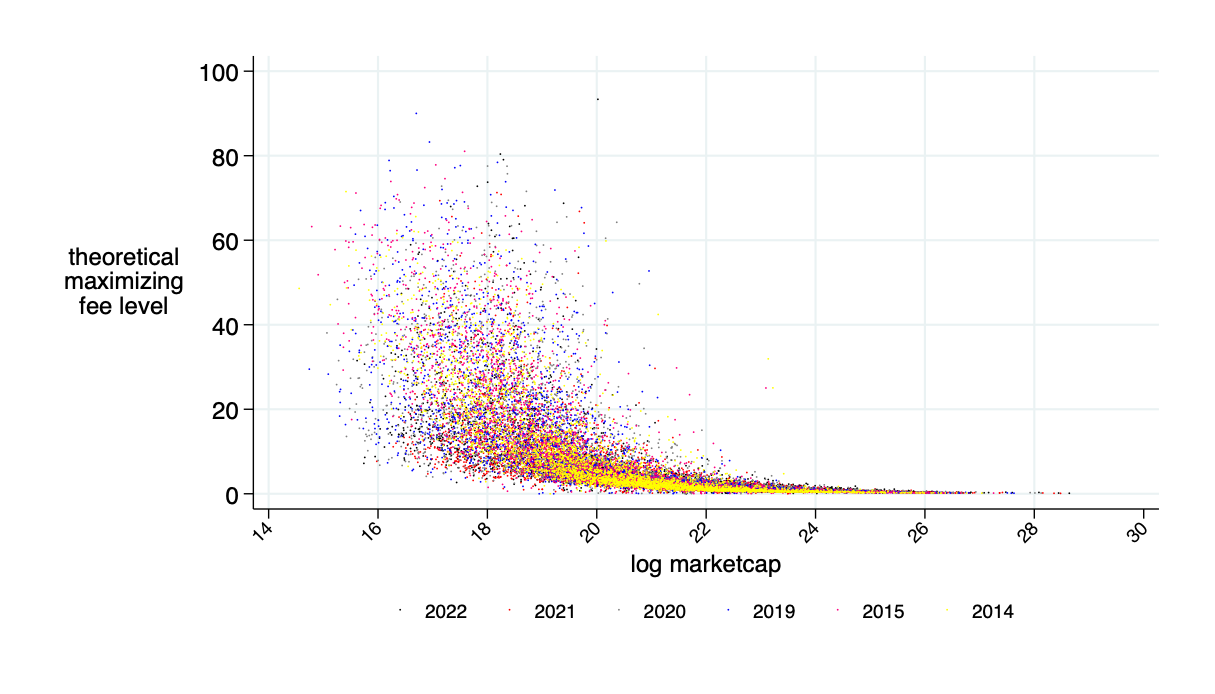
Optimal fee \(F^\pi\)
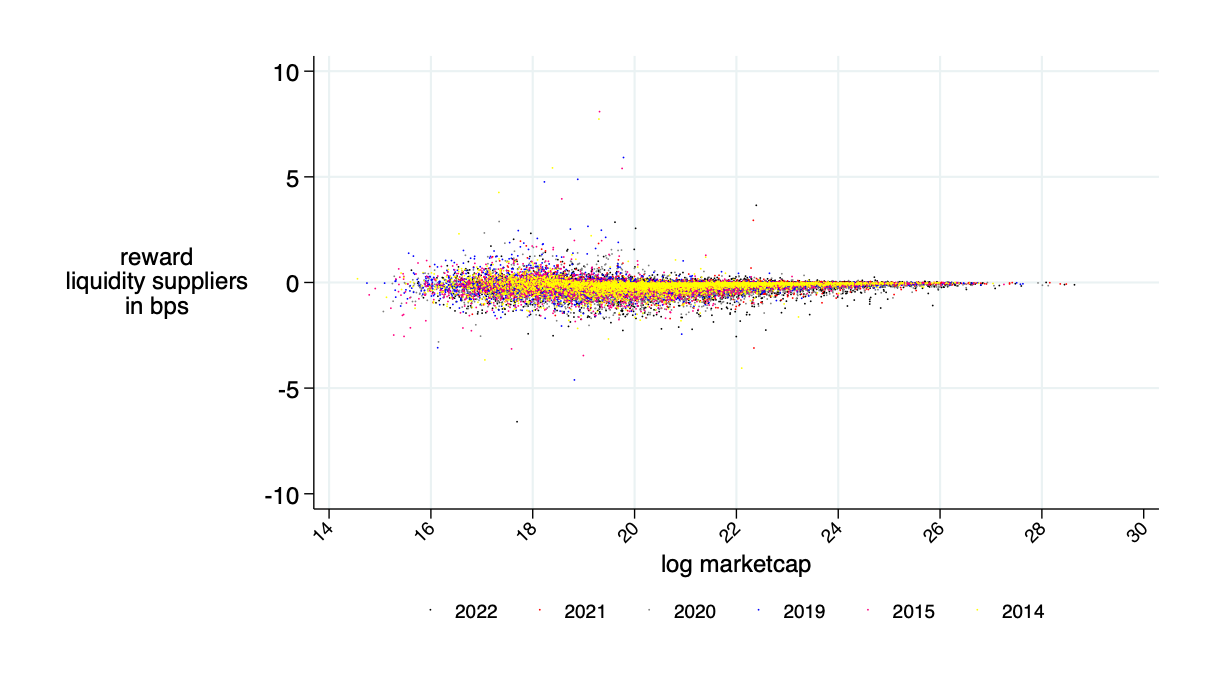
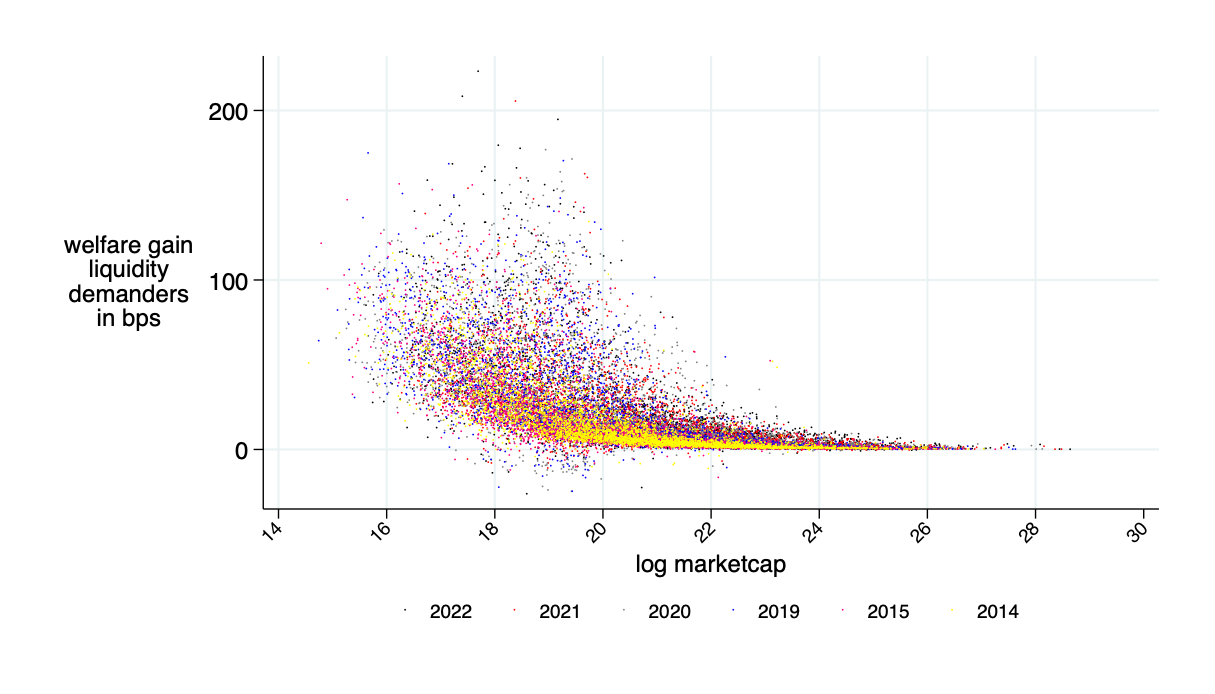
average benefits liquidity provider in bps (average=0)
Insight: Theory is OK - LP's about break even
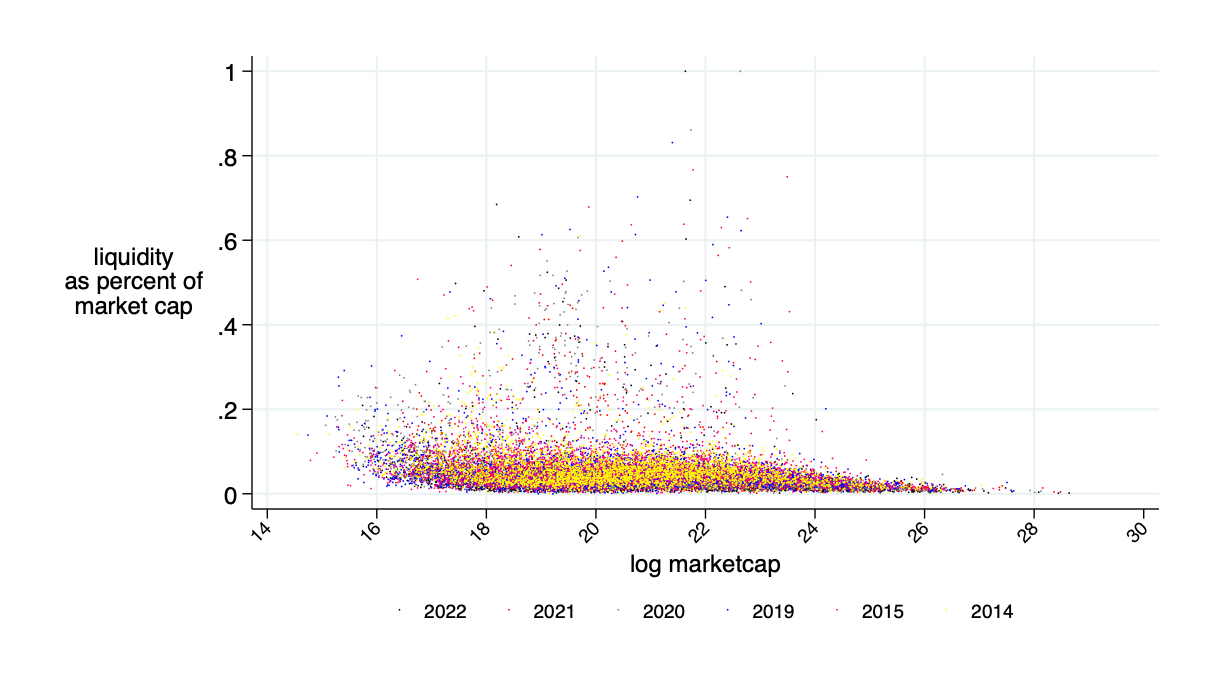
\(\overline{\alpha}\) for \(F=F^\pi\)
Need about 10% of market cap in liquidity deposits to make this work

actually needed cash as fraction of "headline" amount
Only need about 5% of the 10% marketcap amount in cash
AMMs are better on about 85% of trading days
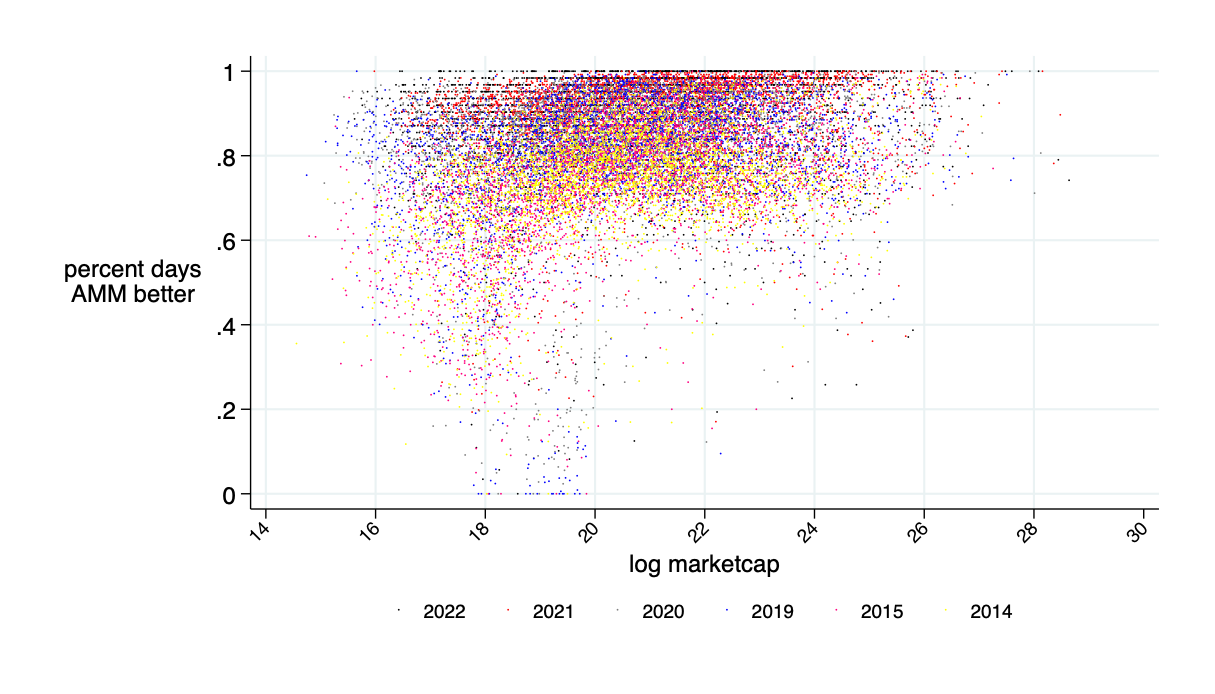
quoted spread minus AMM price impact minus AMM fee (all measured in bps)
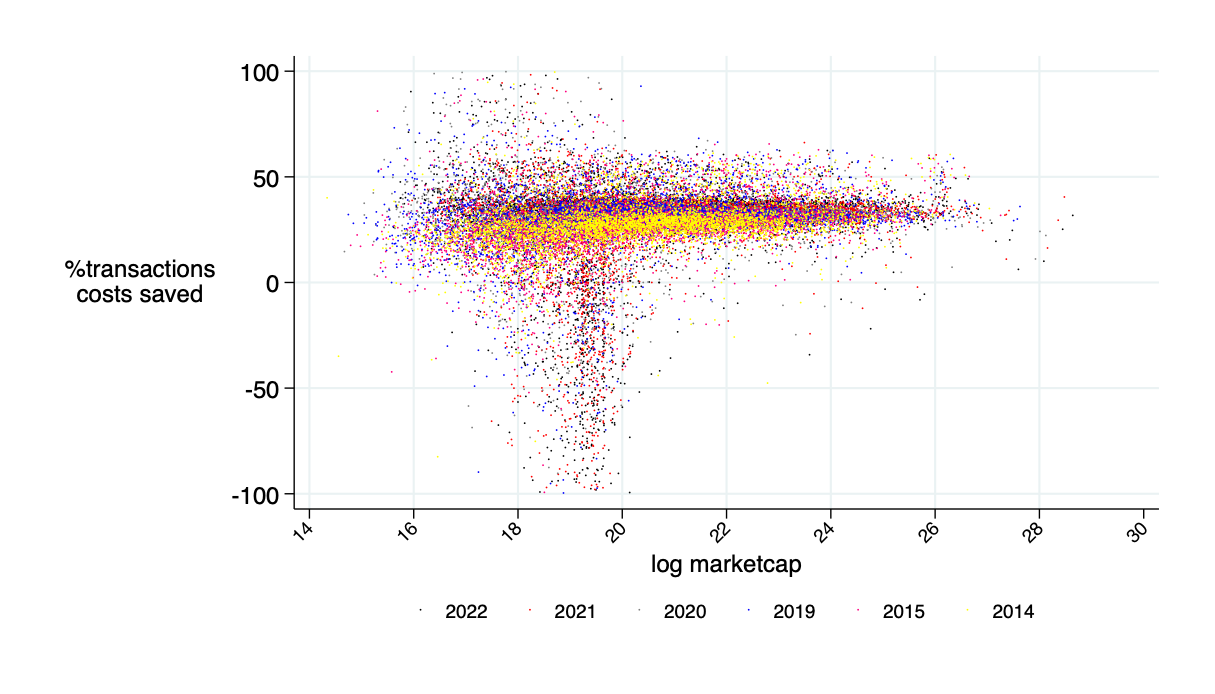
relative savings: what fraction of transactions costs would an AMM save? \(\to\) about 30%
theoretical annual savings in transactions costs is about $15B
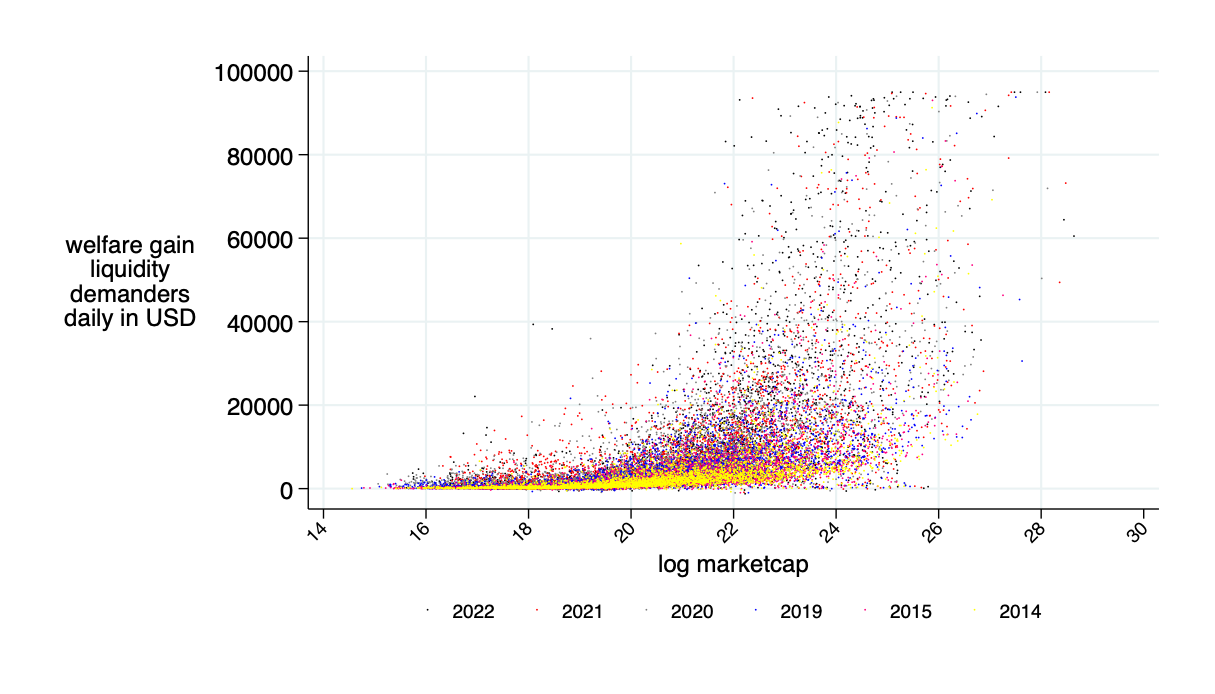
Literature
AMM Literature: a booming field
- Theory
-
Lehar and Parlour (2021): for many parametric configurations, investors prefer AMMs over the limit order market.
-
Aoyagi and Ito (2021): co-existence of a centralized exchange and an automated market maker; informed traders react non-monotonically to changes in the risky asset’s volatility
-
Capponi and Jia (2021): price volatility \(\to\) welfare of AMM LPs; conditions for a breakdown of liquidity supply in the automated system; more convex pricing \(\to\) lower arbitrage rents & less trading.
-
Capponi, Jia, and Wang (2022): decision problems of validators, traders, and MEV bots under the Flashbots protocol.
-
Park (2021): properties and conceptual challenges for AMM pricing functions
-
Milionis, Moallemi, Roughgarden, and Zhang (2022): dynamic impermanent loss analysis for under constant product pricing.
-
Hasbrouck, Rivera, and Saleh (2022): higher fee \(\Rightarrow\) higher volume
-
-
Empirics:
-
Lehar and Parlour (2021): price discovery better on AMMs
-
Barbon and Ranaldo (2022): compare the liquidity CEX and DEX; argue that DEX prices are less efficient.
-
@financeUTM
andreas.park@rotman.utoronto.ca

slides.com/ap248
sites.google.com/site/parkandreas/
youtube.com/user/andreaspark2812/