Learning from DeFi: Would Automated
Market Makers Improve Equity Trading?
Katya Malinova & Andreas Park
WFA 2024
Honolulu, June 28-30, 2024
| McMaster University |
University of Toronto |
|---|
- Blockchain: borderless general purpose value and resource management tool
Preliminaries
- DeFi: financial applications that run on blockchains
- \(\Rightarrow\) brought new ideas and tools
- one new market institution: automated market makers
Decentralized trading using automated market makers (AMM)













Liquidity providers
Liquidity demander
Liquidity Pool

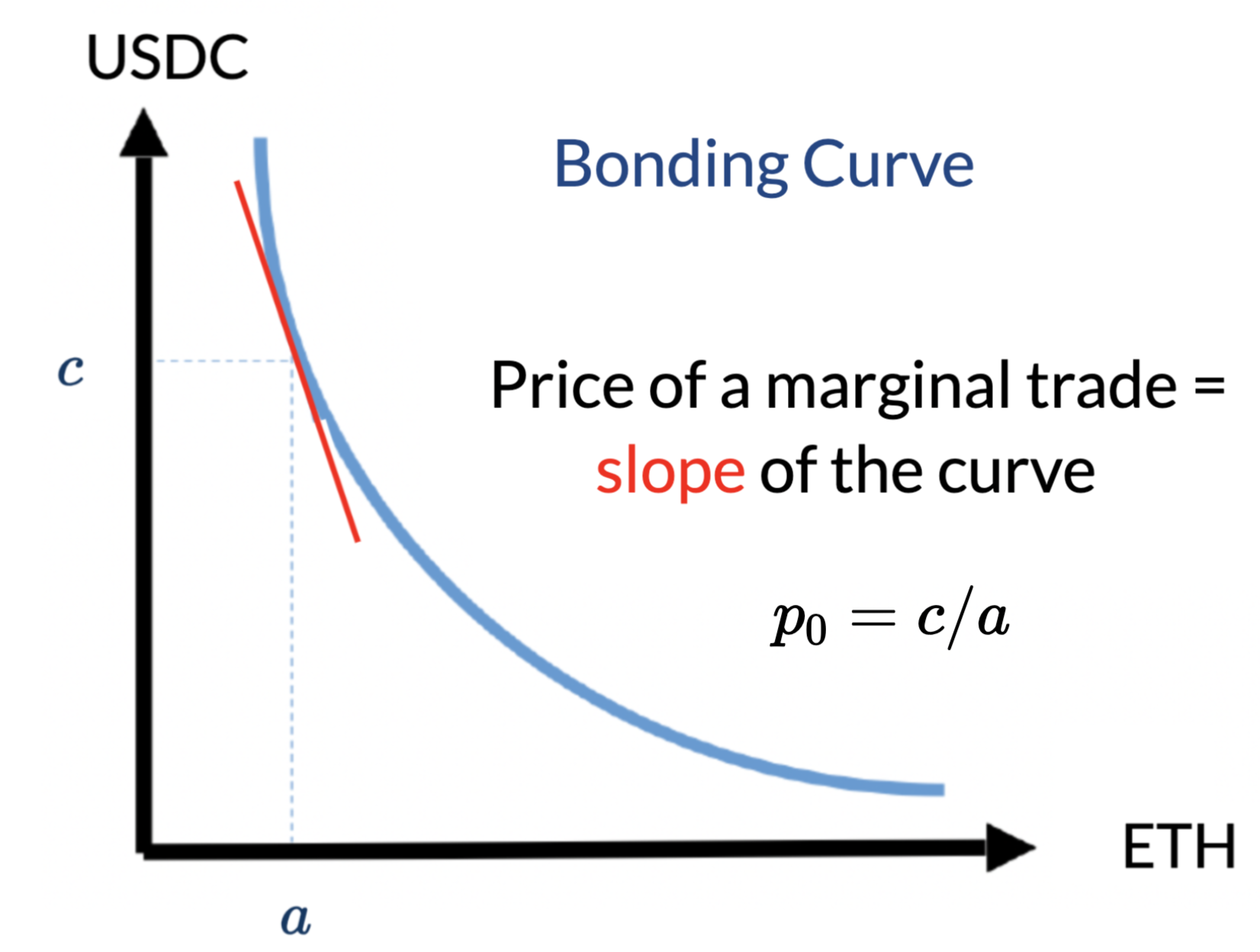
AMM pricing is mechanical:
- determined by the amounts of deposits
- most common:
- constant product
- #USDC \(\times\) #ETH = const
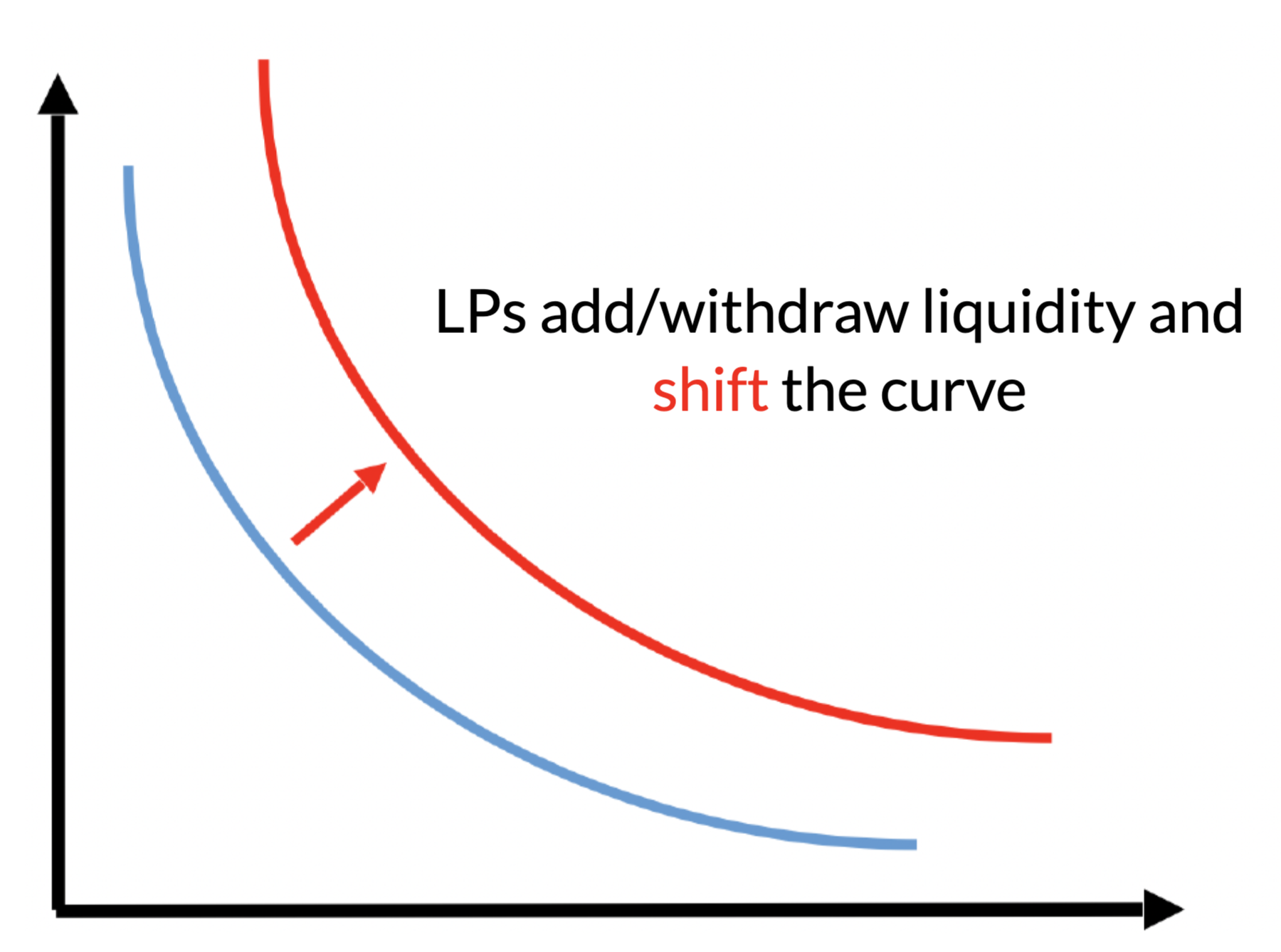
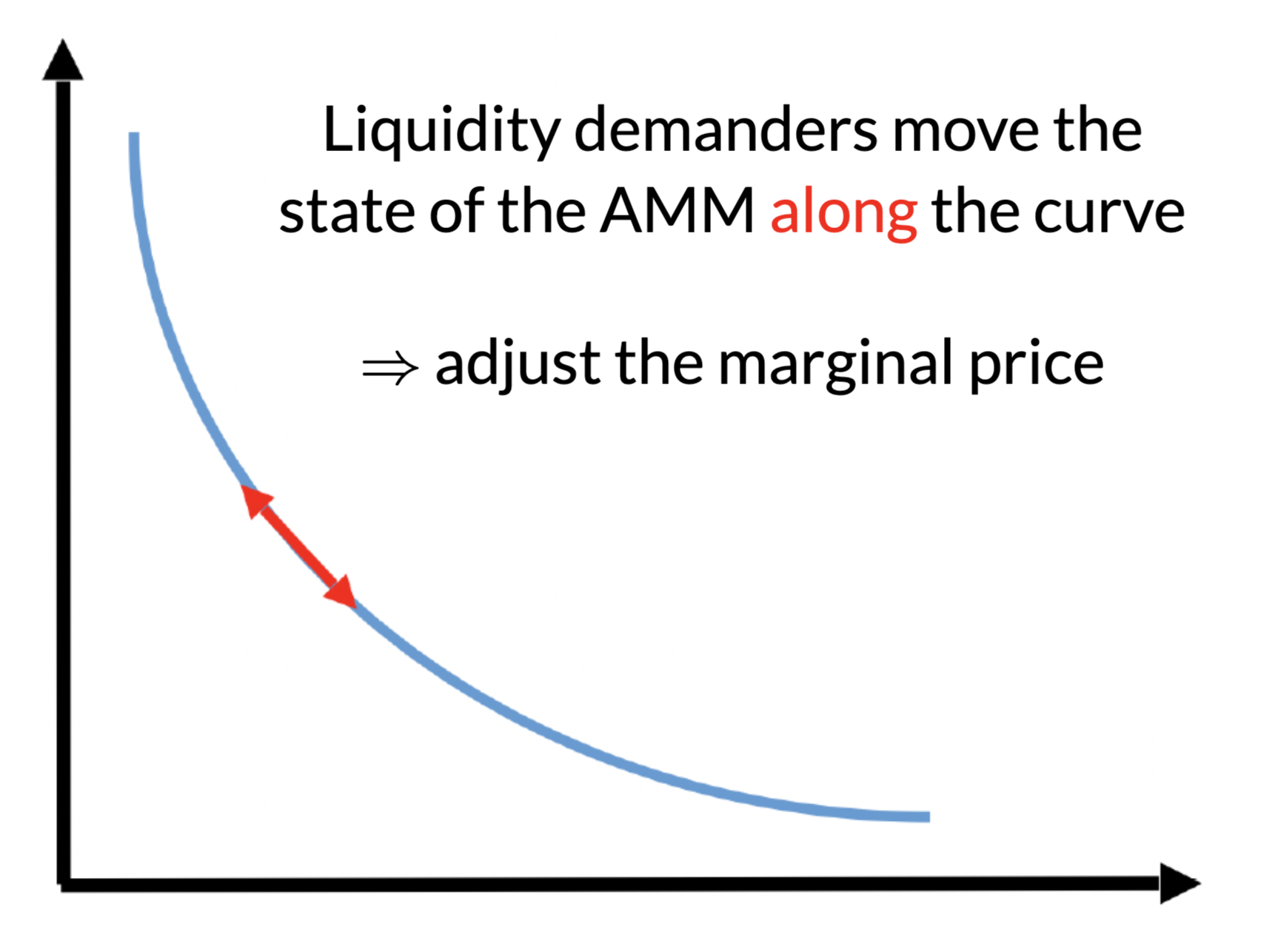
No effect on the marginal price
Key Components
- Our question:
- Can an economically viable AMM be designed for current equity markets?
- Would such an AMM improve current markets?
- Pooling of liquidity!
- Liquidity providers:
- pro-rated
- risk
- trading fee income
- use assets that they own to earn passive (fee) income
- retain exposure to the asset
- pro-rated
- Liquidity demanders:
- predictable price
- continuous trading
- ample liquidity
Existing asset holders, not market makers, do not aim for zero inventory!
Modelling Calibrate-able Liquidity Supply and Demand in an Automated Market Maker
Liquidity providers
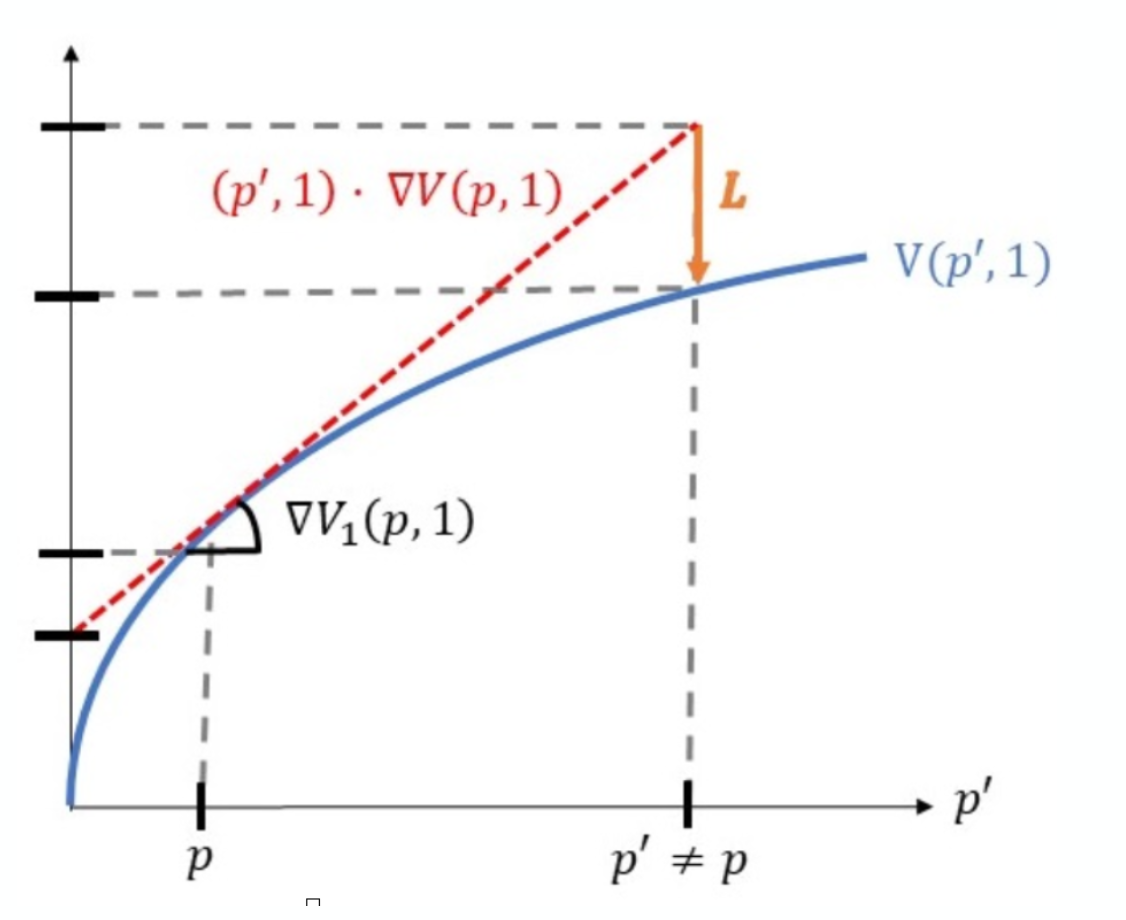
- Deposit asset & cash when the asset price is \(p\)
- While in the pool: balanced volume \(V\) + order imbalance \(p\to p'\)
- Withdraw at price \(p'\)
Buy and hold
Provided liquidity
in the pool
- \(\Rightarrow\) positional loss relative to a "buy-and-hold" when \(p'\ne p\)
- adverse selection
- Arbitrageurs monitor the pool
- \(\Rightarrow\) LPs deposit/writhdraw at efficient prices!
Expected returns to liquidity providers over the "deposit period"
- \(R\) = asset return
- \(F\) = trading fee
- \(V\) = balanced volume
- \(a\) = size of the liquidity pool
Similar to Lehar and Parlour (2023), Barbon & Ranaldo (2022).
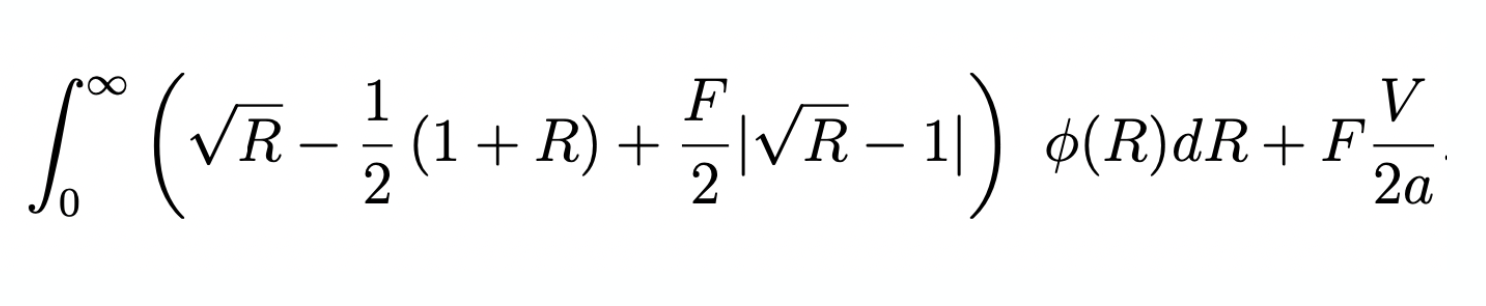
(incremental) adverse selection loss \(L\) when the asset return is \(R=p'/p\)
fees earned
on informed
fees earned
on balanced flow
for reference:
- If the asset price \(\searrow\) 10% the incremental loss \(L\) for liquidity providers is 13 basis points on the deposit
- \(\to\) total loss=-10.13%
- If the asset price \(\nearrow\) 10%, the liquidity provider gains 12 basis points less on the deposit
- \(\to\) total gain =9.88%
For fixed balanced volume \(V\) & fee \(F\):
- Larger pool size \(a \to\) smaller shares of the fees
- \(\Rightarrow \) LP return \(\searrow\) in pool size
-
Competitive liquidty provision:
- \(\Rightarrow\) the upper-bound on pool size above which LPs lose money
- we characterize this by \(\bar{\alpha}\) \(=\) fraction of the asset's market cap to be deposited to the pool
\(=\) 0
Liquidity Demander's Decision & (optimal) AMM Fees
- Better off with AMM relative to traditional market if
\[\text{AMM price impact} +\text{AMM fee } F \le \text{bid-ask spread}.\]
- Two opposing forces when fee \(F\nearrow\)
- more liquidity provision
\(\to\) lower price impact - more fees to pay
- more liquidity provision
Result:
competitive liq provision\(\to\) there exists an optimal (min trading costs) fee \(F >0\)
- \(\to\) derive closed form solution
- Fee \(F\) depends on asset return distribution, balanced volume, quantity demanded
Similar to Lehar&Parlour (2023) and Hasbrouck, Riviera, Saleh (2023)
- Optimal \(F\) is asset-specific to compensate LPs for asset-specific adverse selection losses!
- Assumption: asset returns are exogenous to trading (efficient prices)
What's next?
- Calibrate to stock markets
- AMM Feasible?
- Are the AMM costs at the optimal fee \(F\) \(<\) bid-ask spread?
Approach: daily AMM deposits
- AMMs close overnight.
- Market: opening auction \(\to\) \(p_0\)
- Determine optimal fee \(F\);
LPs deposit \(a\) assets and \(c\) cash at ratio \(p_0=c/a\) until break even \(\alpha=\overline{\alpha}\)
- Liquidity locked for the day
- At EOD release deposits and fees
- Back to 1.
Background on Data
Special Consideration 1: What volume?
-
some volume may be intermediated
- with AMMs: no need for intermediation
- \(\to\) intermediated volume could disappear
- \(\to\) use volume/2
- Some caveats, e.g.
- arbitrageur volumes
- larger volume if AMM has lower trading costs
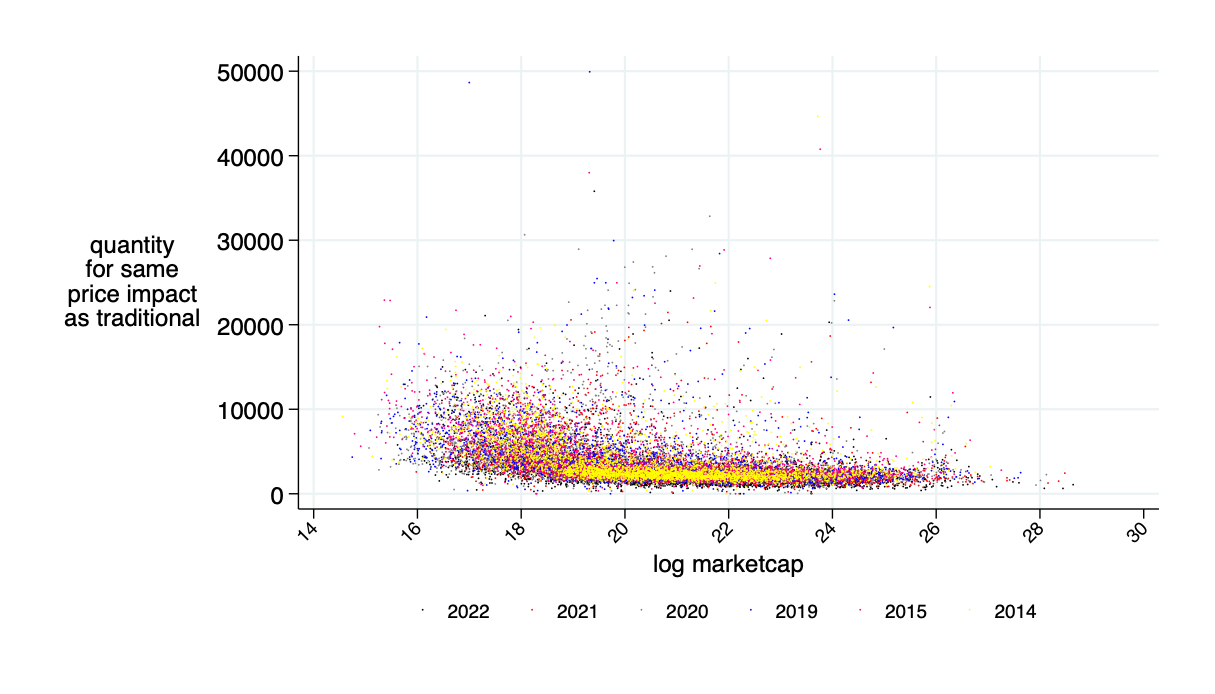
Special Consideration 2: What's \(q\) (the representative order size)?
- use average per day
- take long-run average + 2 std of daily averages
- (also avg \(\times 2\),\(\times 4\), depth)
All displayed data CRSP \(\cap\) WRDS
- CRSP for shares outstanding
- WRDS-computed statistics for
- quoted spreads (results similar for effective)
- volume
- open-to-close returns
- average trade sizes, VWAP
- Time horizon: 2014 - March 2022
- Exclude "tick pilot" period (Oct 2016-Oct 2018)
- All common stocks (not ETFs) (~7550).
- Explicitly not cutting by price or size
- All "boundless" numbers are winsorized at 99%.
Special Consideration 3:
Where to get returns and volume?
- Approach 1: "ad hoc"
- "one-day-back" look
- take yesterday's return and volume when deciding on liquidity provision in AMM
- Approach 2: estimate historical return distribution
AMMs based on historical returns
- average \(F^\pi=11\)bps
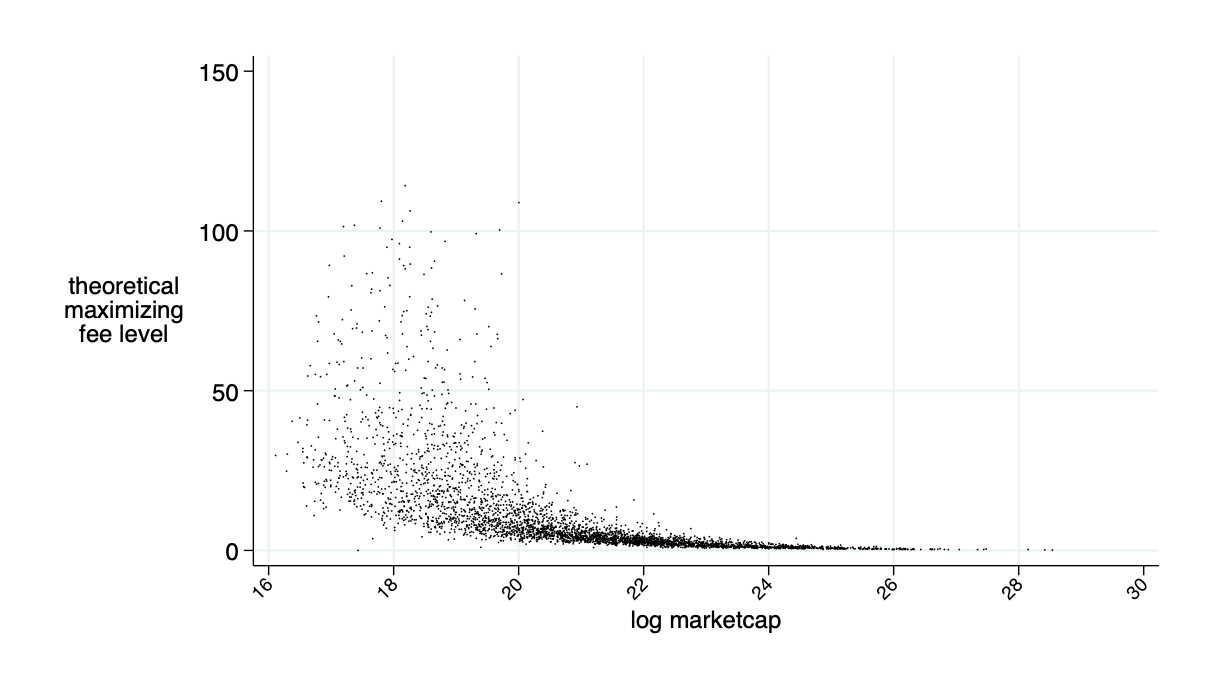
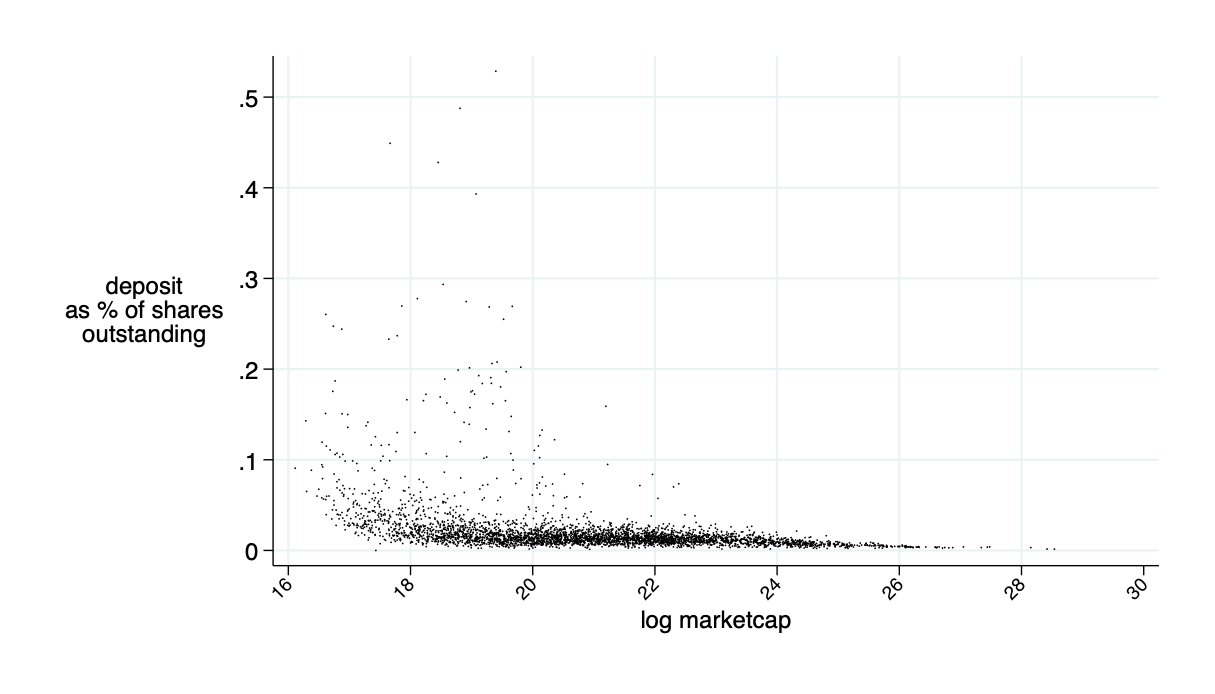
Average of the market cap to be deposited for competitive liquidity provision: \(\bar{\alpha}\approx 2\%\)
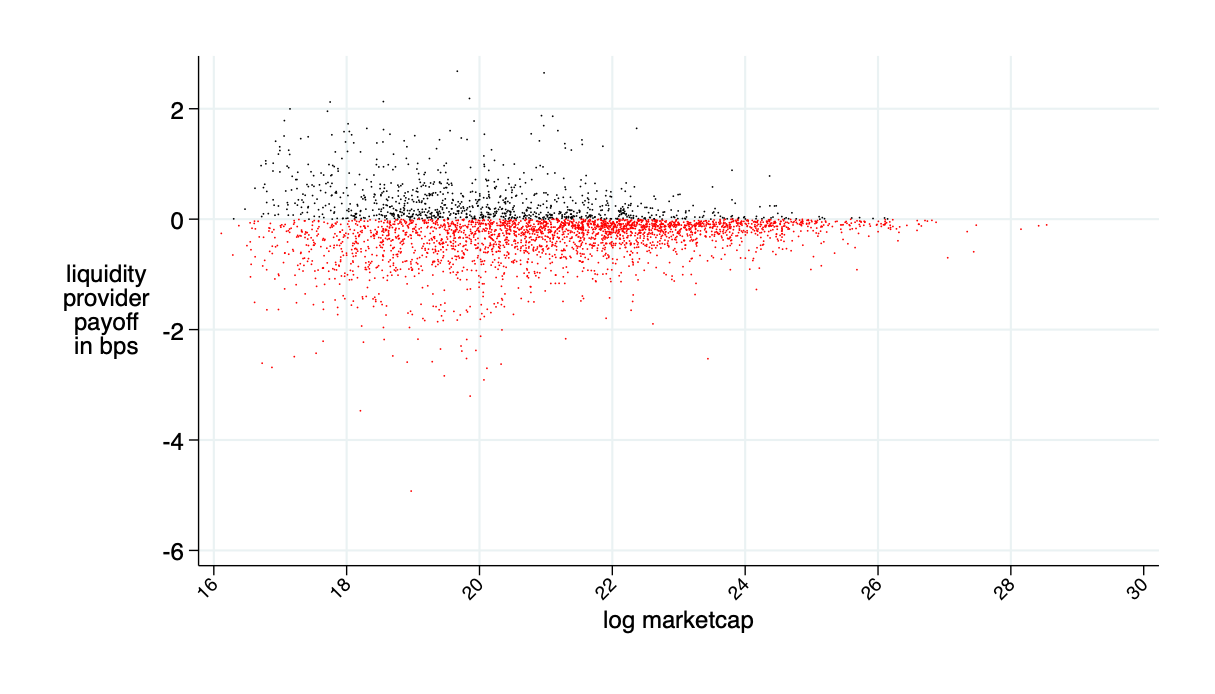
almost break even on average (average loss 0.2bps \(\approx0\))
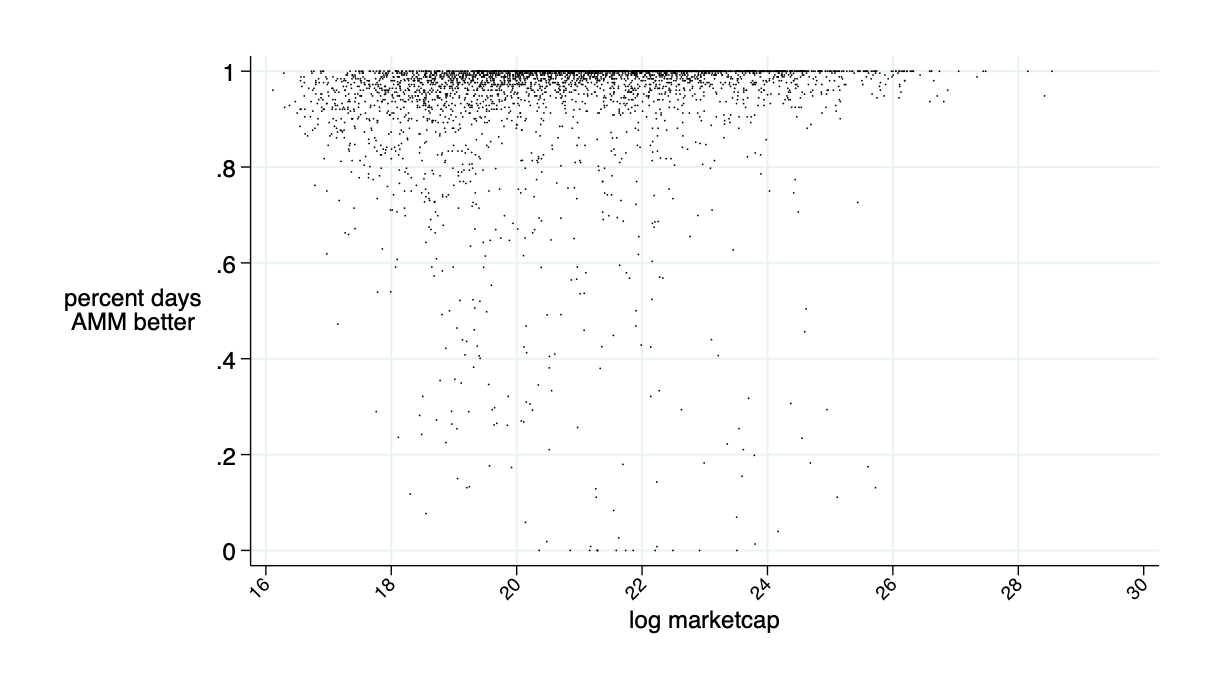
average: 94% of days AMM is cheaper than LOB for liq demanders
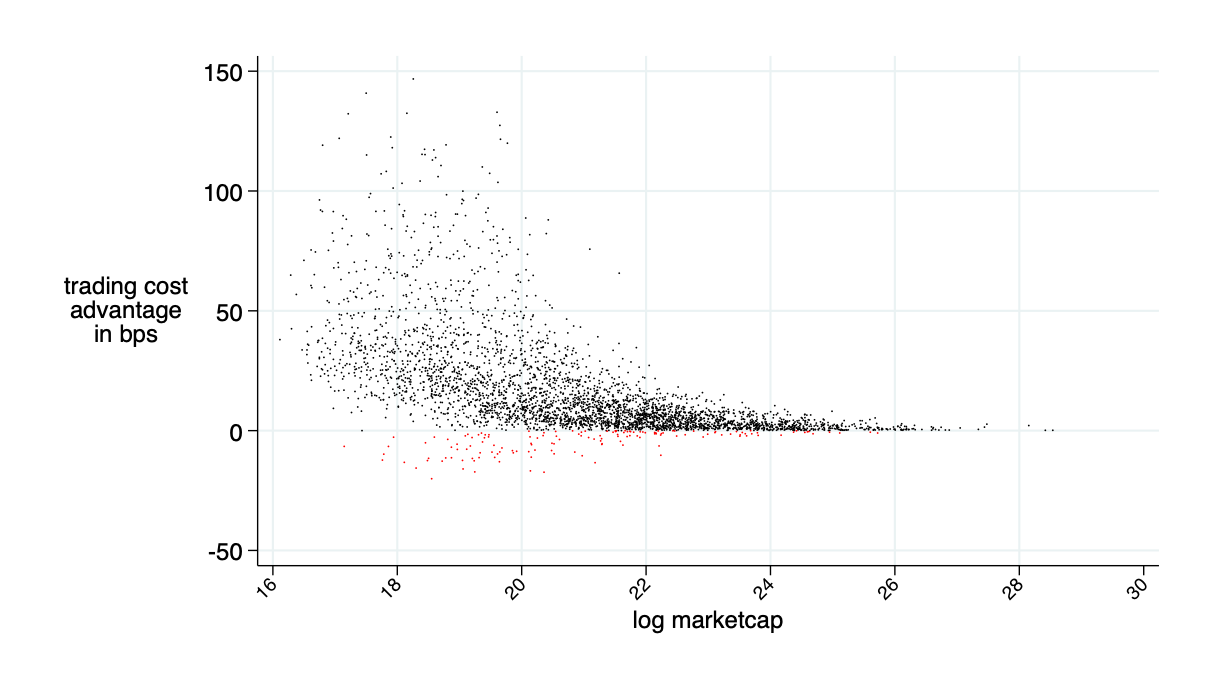
average savings: 16 bps
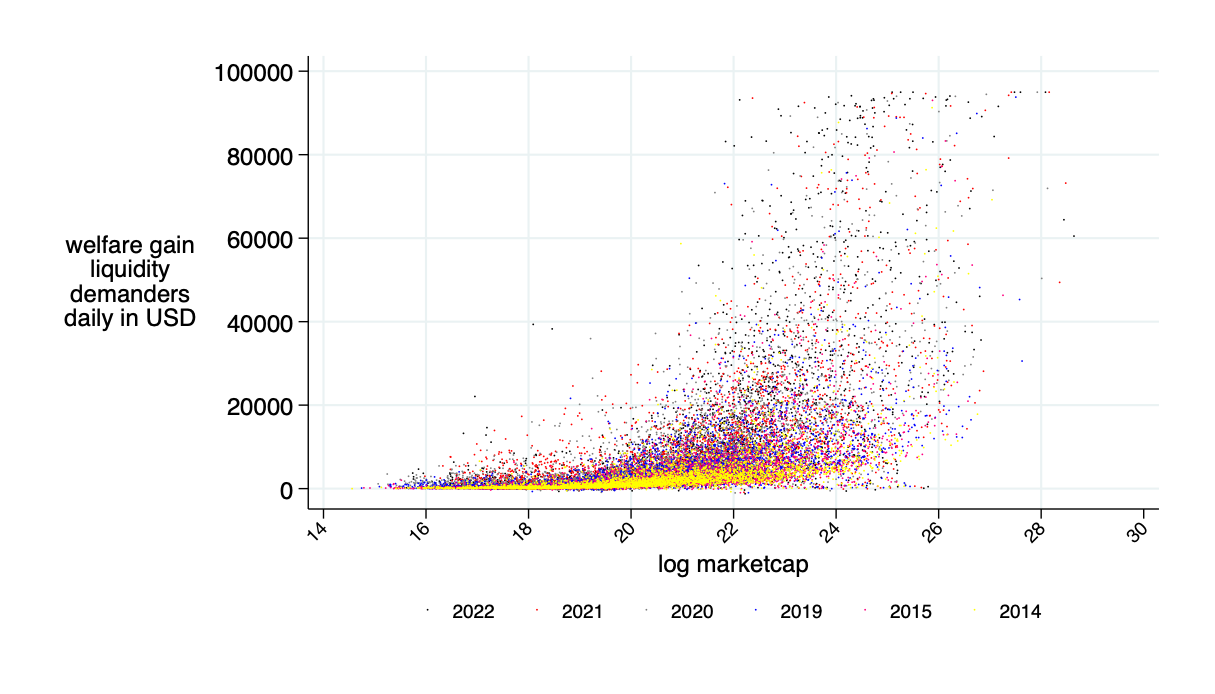
average daily: $9.5K
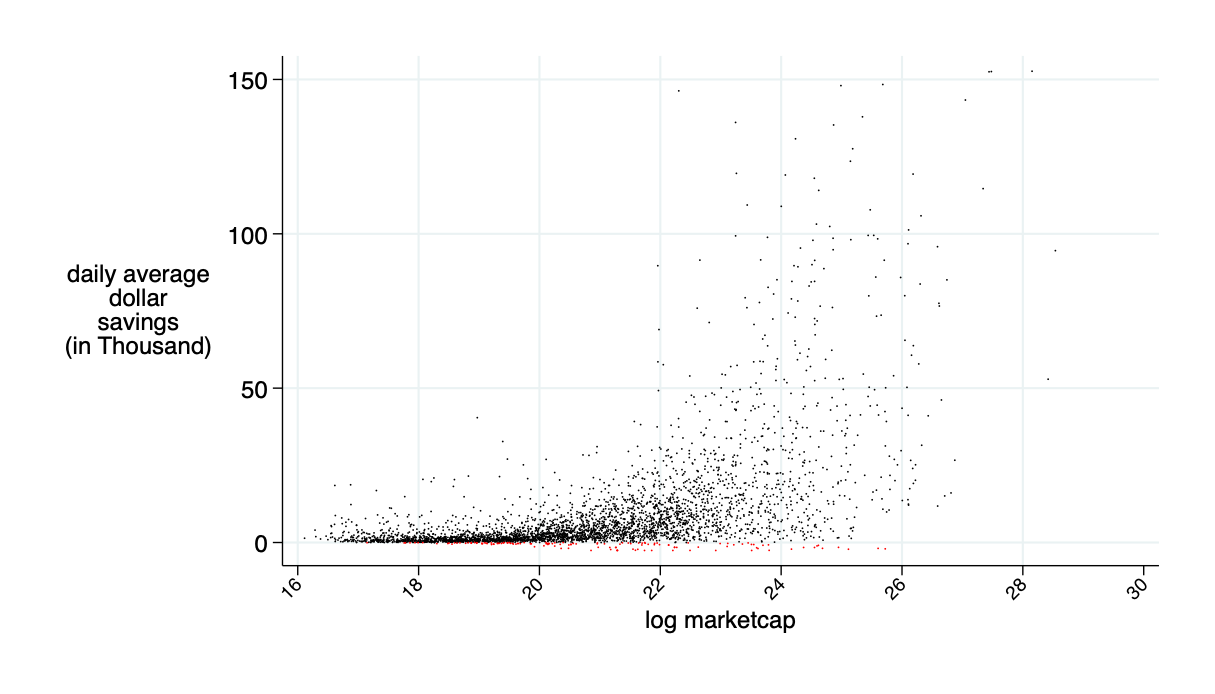
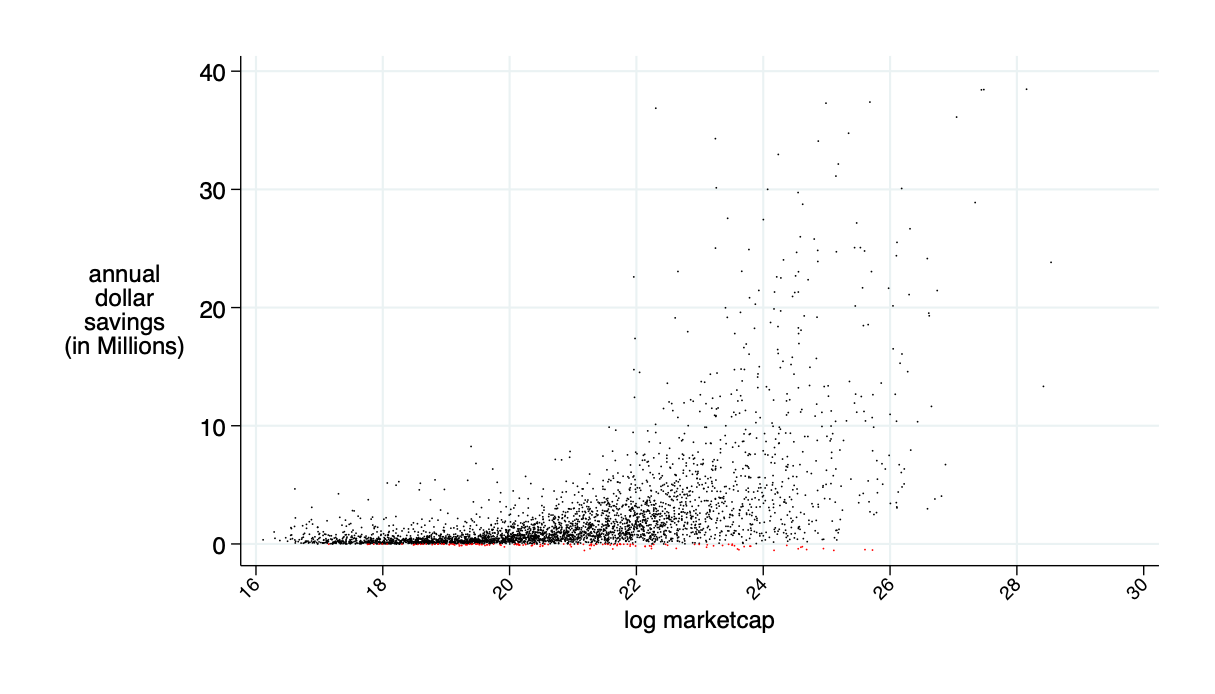
average annual saving: $2.4 million
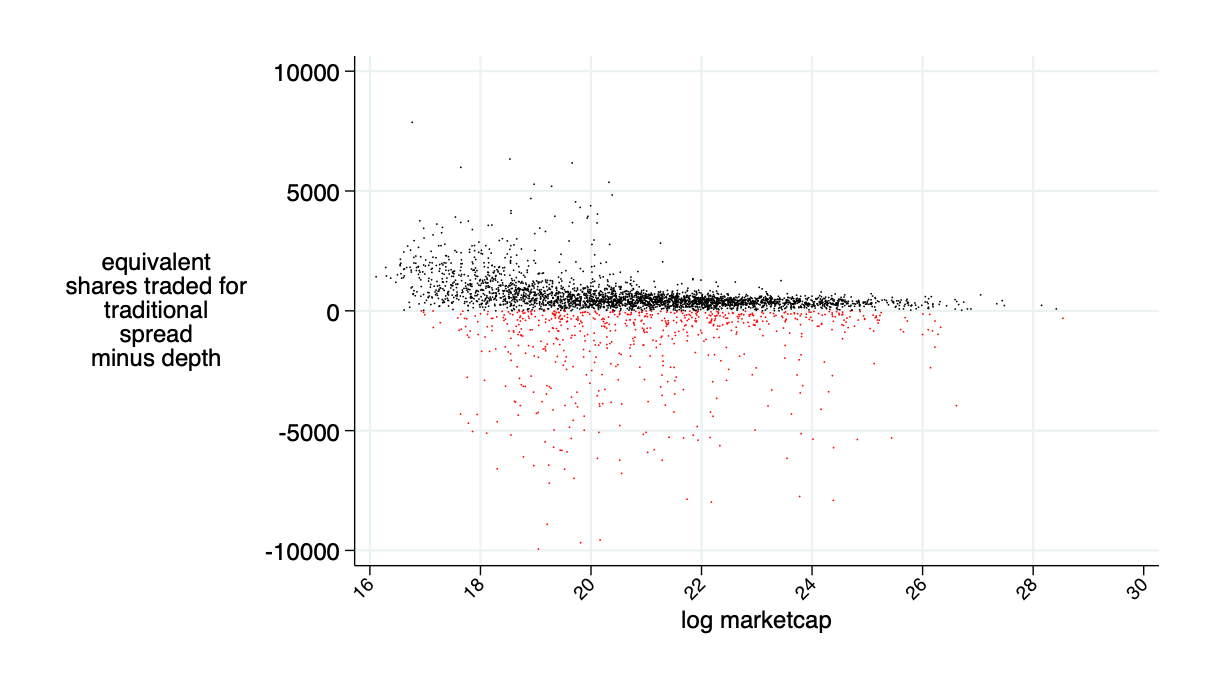
implied "excess depth" on AMM relative to the traditional market
Sidebar: Cash deposit requirements
- Asset provision is not a problem: enough idle liquidity
-
But: AMM requires off-setting cash: \(c =a\cdot p(0)\).
- Cash is not free: at 6% annual rate, 2bps per day.
- Adds to fees
- Several solutions:
- Narrow a range of returns for which to provide liquidity (akin to Uniswap V3) or circuit breakers
- Other mechanisms being developed
- Balancer protocol: same cash for many assets
\(\Rightarrow \) Need about 5% of the value of the shares deposited -- not 100% -- to cover up to a 10% return decline
Summary
- AMMs do not require a blockchain - just a concept
- could be run in the existing world (though there are institutional and regulatory barriers)
- Our question:
- Can an economically viable AMM be designed for current equity markets?
- Would such an AMM improve current markets?
- Answers:
- Yes.
- Massively.
- Source of Savings:
- Liquidity providers \(\not=\) Citadel!
- \(\to\) no (overnight) inventory costs
- \(\to\) use idle capital
- \(\to\) + better risk sharing
@katyamalinova
malinovk@mcmaster.ca

slides.com/kmalinova
https://sites.google.com/site/katyamalinova/
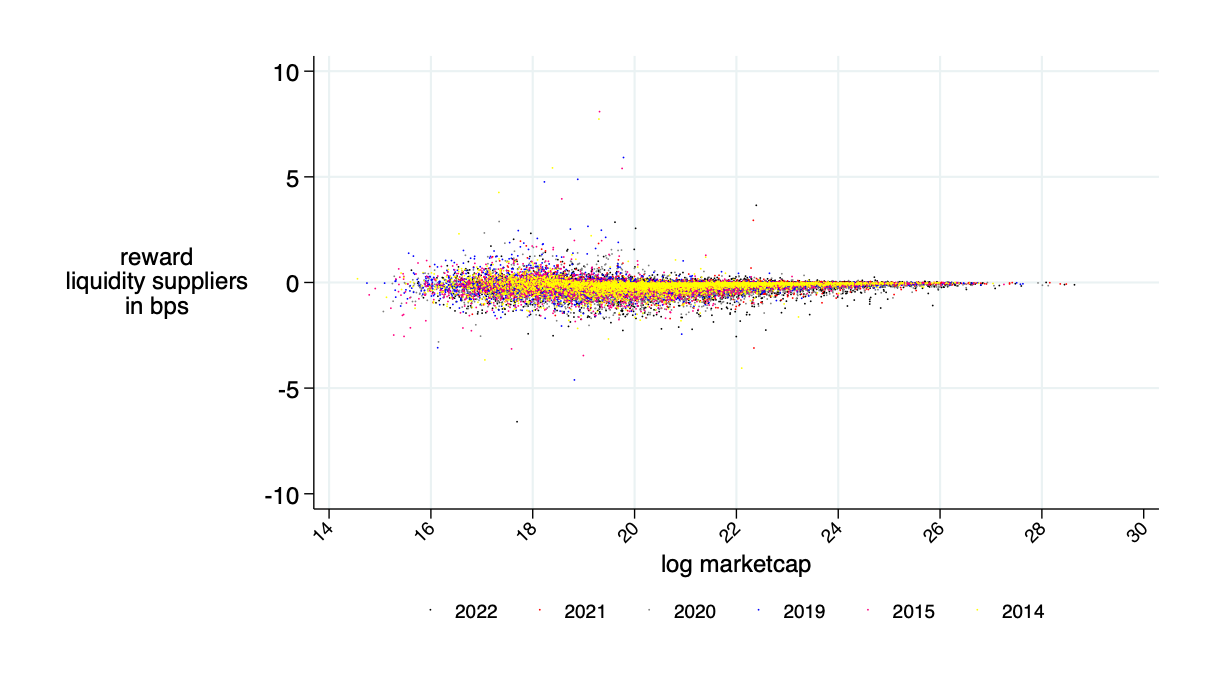
Optimal fee \(F^\pi\)
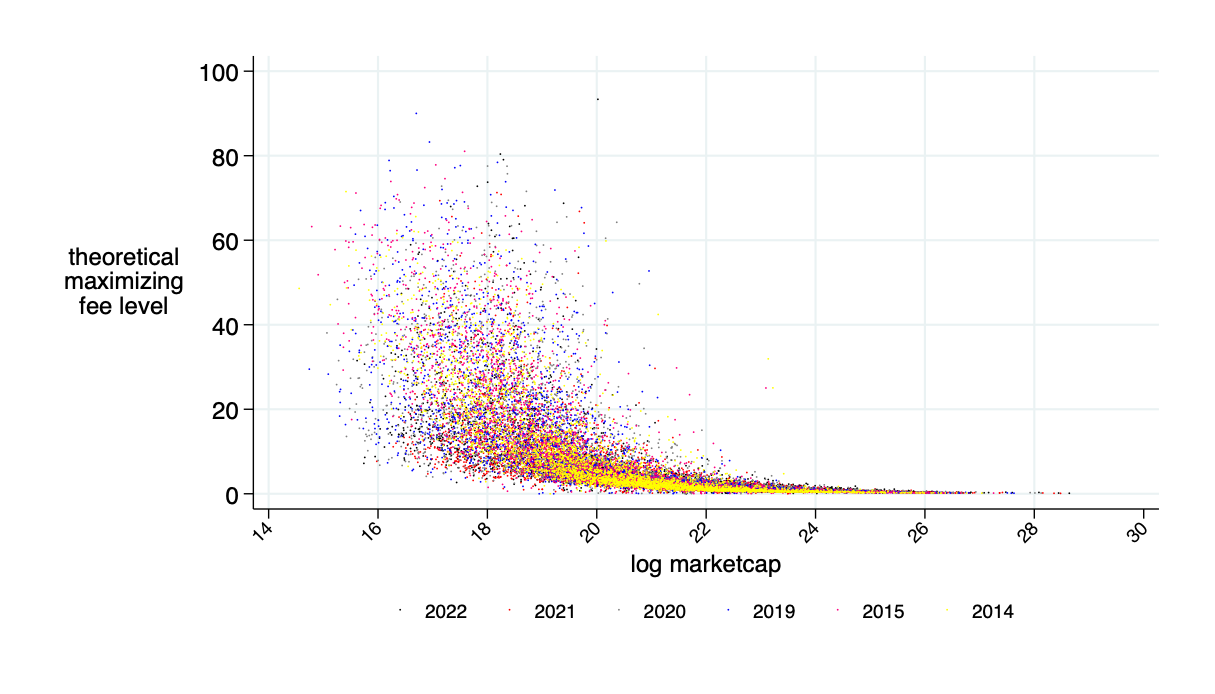
average benefits liquidity provider in bps (average=0)
Insight: Theory is OK - LP's about break even
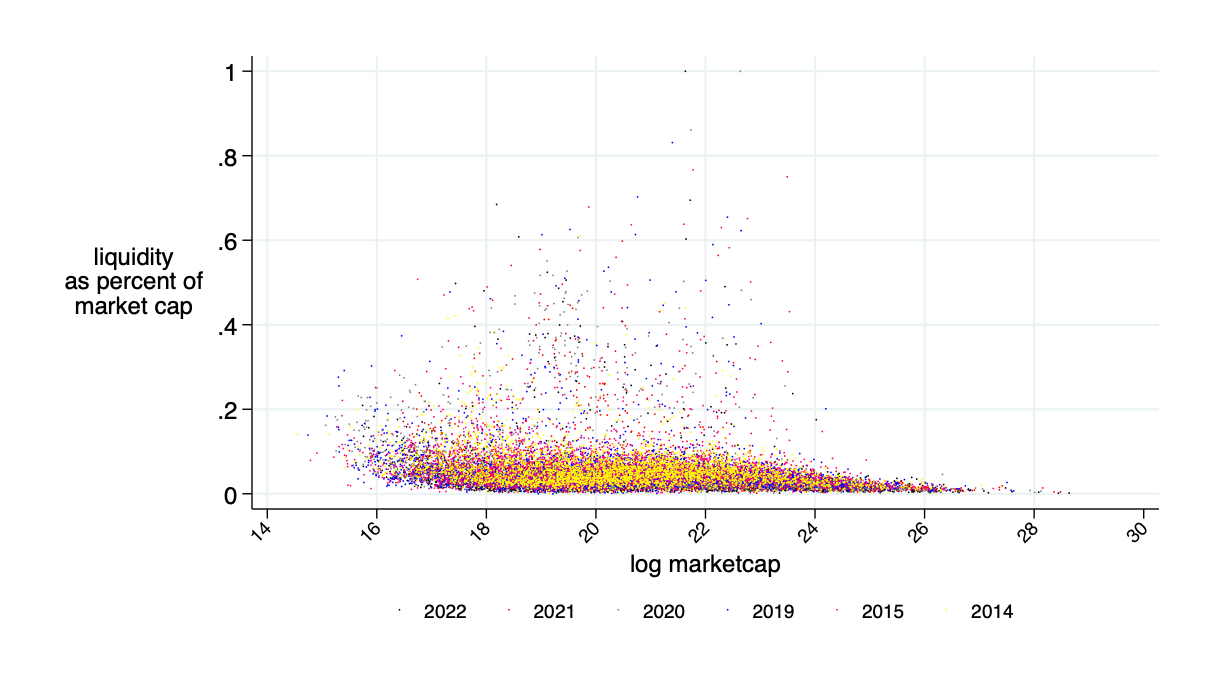
\(\overline{\alpha}\) for \(F=F^\pi\)
Need about 10% of market cap in liquidity deposits to make this work
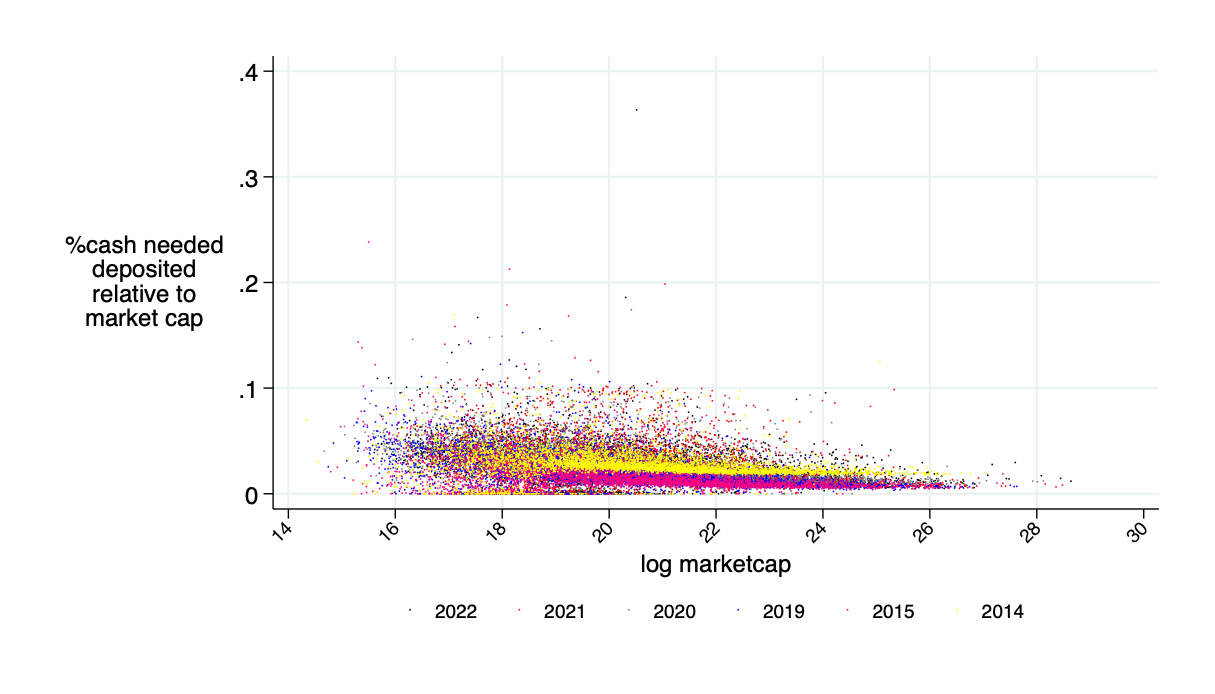
actually needed cash as fraction of "headline" amount
Only need about 5% of the 10% marketcap amount in cash
AMMs are better on about 85% of trading days
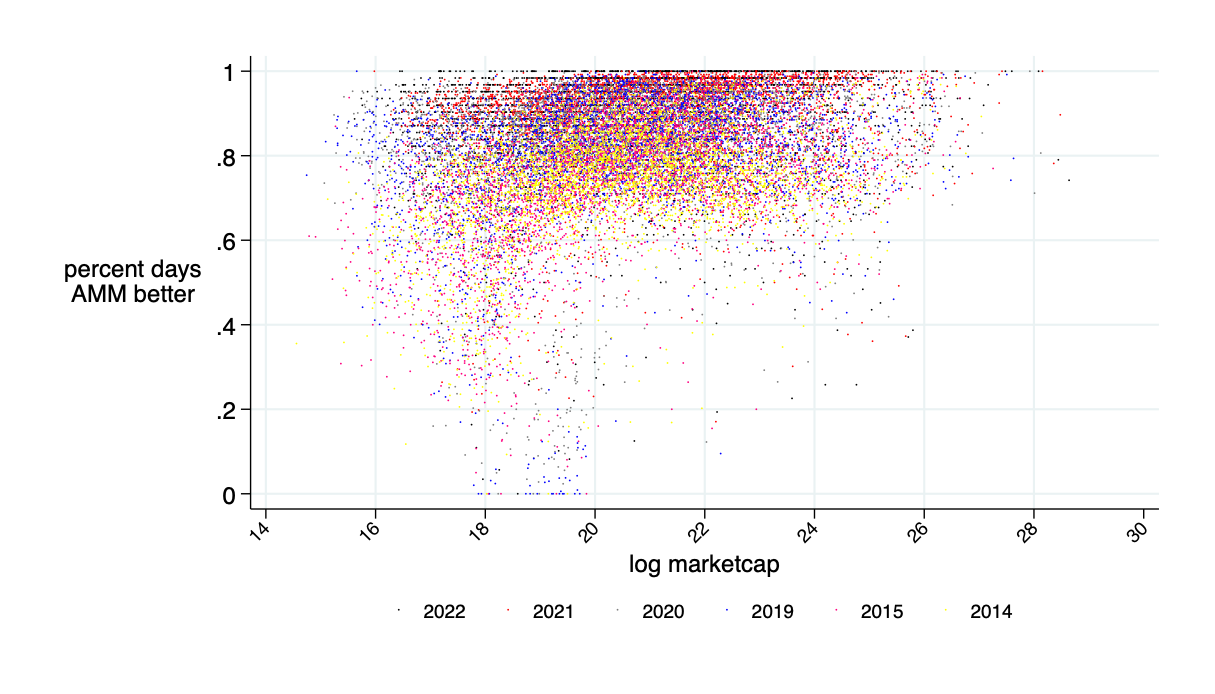
quoted spread minus AMM price impact minus AMM fee (all measured in bps)
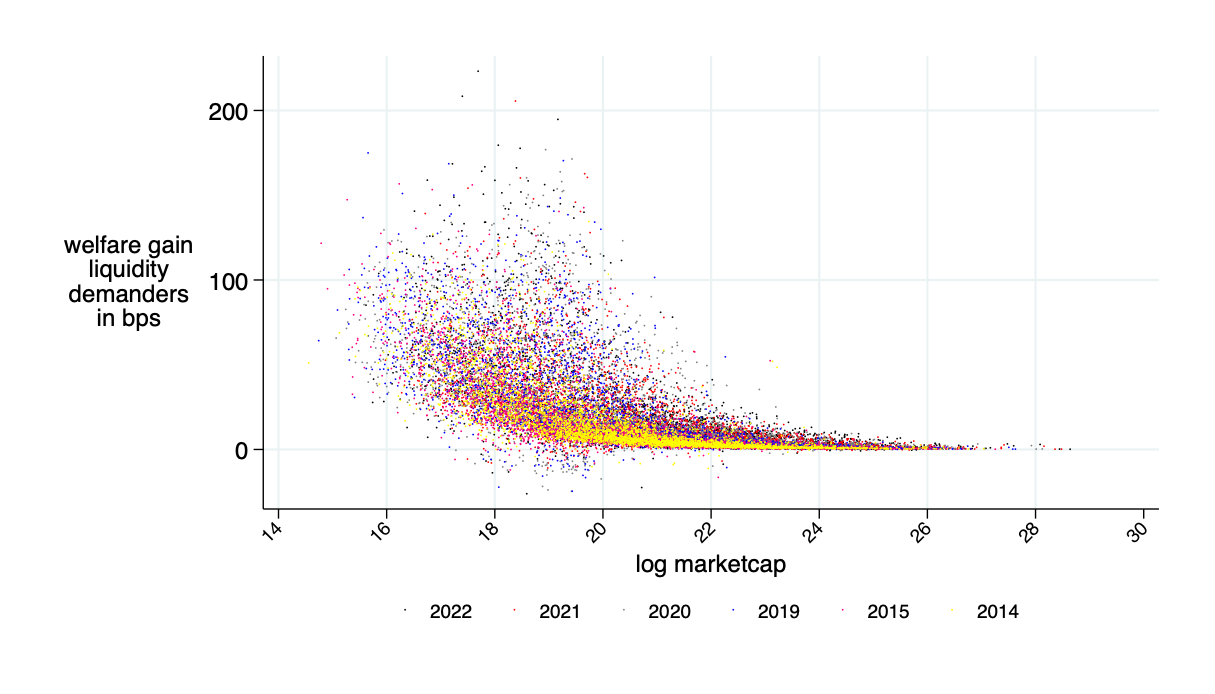
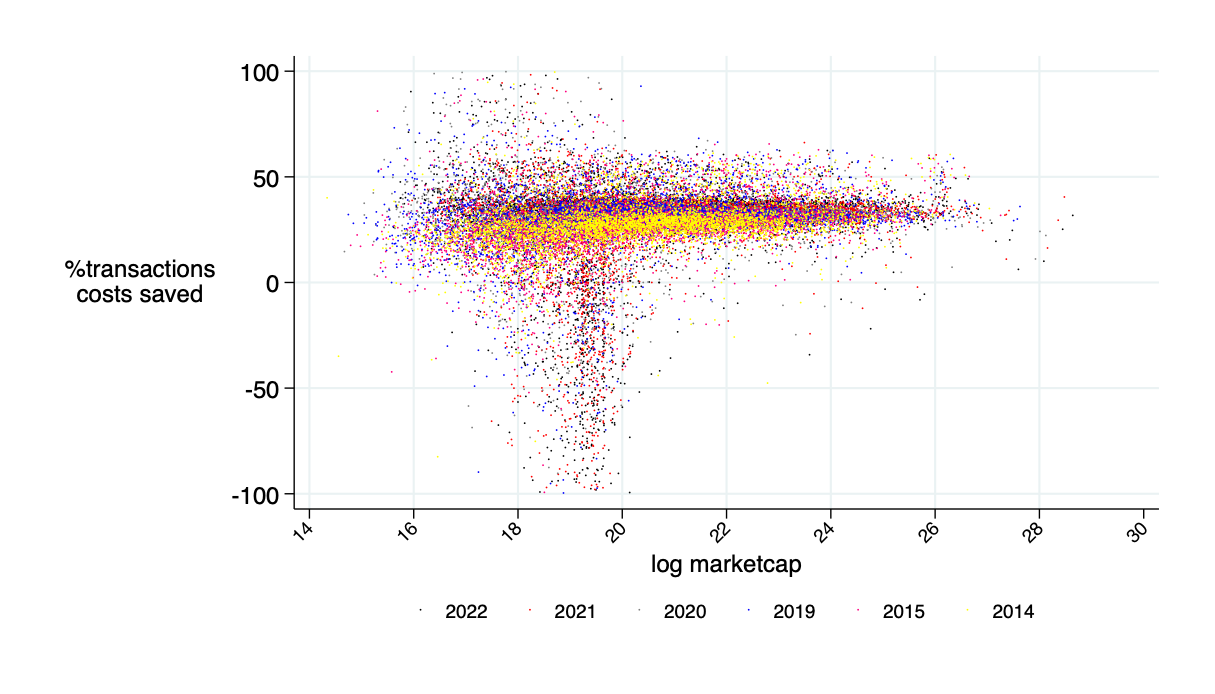
relative savings: what fraction of transactions costs would an AMM save? \(\to\) about 30%
theoretical annual savings in transactions costs is about $15B