Tokenomics:
When Tokens Beat Equity
Katya Malinova & Andreas Park
Digital Economy Seminar Series, July 08 2021
Key Challenges for the Crypto Community
Technology
Legal/Regulation
Economic functions





What is the right governance structure for systems?
\(\Rightarrow\) political economy
How should we design tokens as contracts?
\(\Rightarrow\) corporate finance
How do platform payment means interact with outside world
\(\Rightarrow\) open-economy macro
How much do we have to pay operators to maintain the chain?
\(\Rightarrow\) mechanism design
Key Economic Questions for Blockchain Design




Cumulative token sales 2016-2018
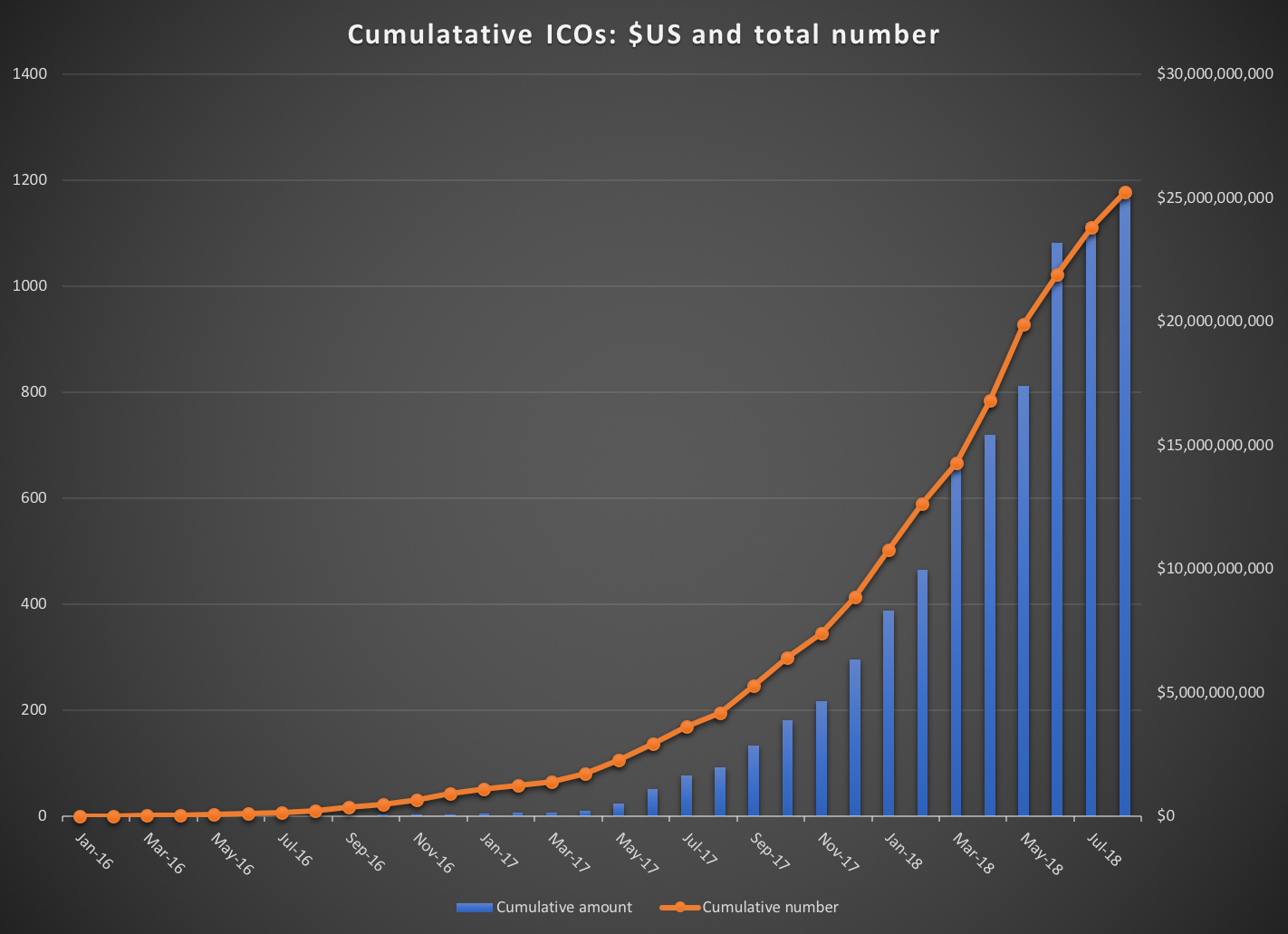
$25B total
$21B in 2018
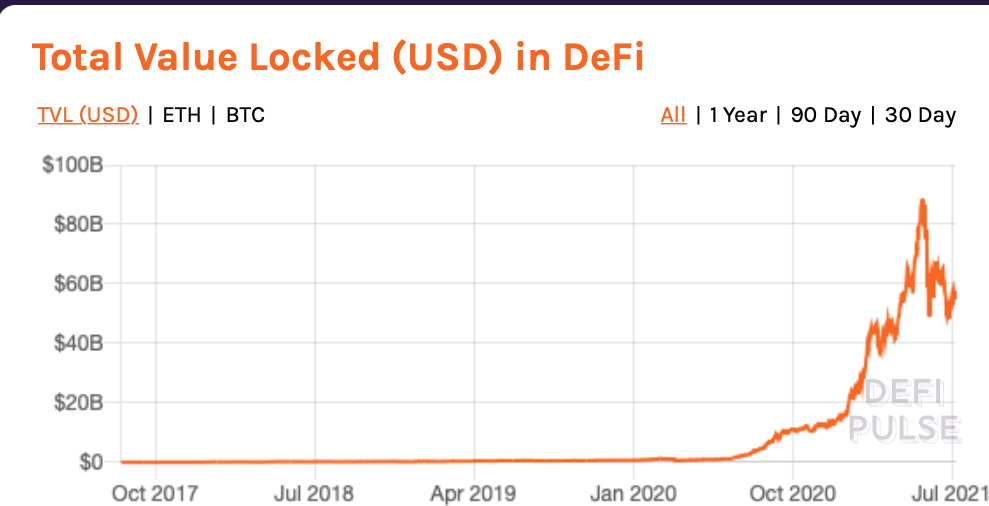
Crypto markets are staging a comeback ... this time in "Decentralized Finance"
https://defipulse.com
Is there economic merit to tokens?
Do tokens solve an economic problem?




State of Debate on Tokens
Financing mechaniPlatforms
Literature
Sockin and Xiong (2018)
Li and Mann (2020)
Bakos and Halaburda (2019)
Cong, Li, and Wang (2018)
Canidio (2020)
Chod, Trichakis, Yang (2019)
Catalini and Gans (2019)
Chod and Lyandres (2020)
Davydiuk, Gupta, and Rosen (2019)
Lee and Parlour (2019)
Garratt and van Oordt (2019)
Gan, Tsoukalas, Netessine (2021)
Financing mechanism
Platforms
Blockchain Tech Stack: Where would tokens matter?
Infrastructure
reward and
internal currency
usage fee
or
incentive
usage fee
Service
Application
Tech Stack Layer
Role of Token
A typical utility or equity token:

Or Future Users

Can be traded right away
May get listed on an exchange
more credibility
Rights to future cashflows from the project
A Simple Model of Token-Based Financing
entrepreneur wants to produce a good or service
Setup cost for production \(C_0\)
Marginal cost of producing \(c\)
Demand is uncertain: revealed after the setup cost has been paid but before production.
Inverse demand \(p(q)=x-q\)
\( x\) is uniform on \([0,\theta]\).
\(x_i\)
\(x_j\)
\(x_k\)
\(c\)
price
If financing with own funds
\(\Rightarrow\) entrepreneur
maximizes monopoly profits
\[\max_q (x-q)\cdot q -cq.\]
\(\Rightarrow\) produces
monopoly quantity
demand
marginal cost
marginal revenue
\(q^m=(x-c)/2\)
\(MR=x-2q\)
\(p(q)=x-q\)
Benchmark: own funds
price
entrepreneur gives \(\alpha\) to equity investors to raise \(C_0\)
investors fund as long as they break even
entrepreneuer maximizes \[\max_q (1-\alpha)( (x-q)\cdot q -cq).\]
demand
marginal revenue
\(\Rightarrow\) max \((1-\alpha)\)(monopoly profits)
=> same as with own funds
=> no distortion
\(q^e=q^m=(x-c)/2\)
\(MR=x-2q\)
\(p(q)=x-q\)
Benchmark: equity
general idea: sell future output
two approaches for token sales
sell a fraction of future revenue
sell units of future output
Token Financing
- we call it revenue sharing
- formally: sell \(\alpha_t\) of \(T\) tokens
- produce \(q\) units a require \(T/q\) tokens per unit
- we call this output presale
- formally: sell \(t\) tokens
- produce \(q\) units and keep revenue from \(q-t\) tokens
price
demand
marginal cost
marginal revenue
Entrepreneur does not internalize the effect of an extra output unit on the token value for the tokenholders!
Result: overproduction
entrepreneur issues \(t\) tokens
for \(x\le t\): earns zero
for \(x>t\): solves \[\max_q (q-t) (x-q)-cq.\]
\(MR(q^{ps})+t=c\)
\[\Rightarrow q^{ps}=\frac{x-c+t}{2}>q^m\]
Output Presale
\(q^{ps}>q^m\)
price
demand
marginal cost
marginal revenue
\(\Rightarrow\) "tilts" marginal revenue for
entrepreneuer left because
get only fraction of revenue
\(\Rightarrow\) solves \((1-\alpha)\)MR(\(q^{rs}\)) = c
\[\Rightarrow q^{rs}=\frac{x-c/(1-\alpha_t)}{2}<q^m\]
Result: underproduction
NB: Similar to underinvestment in Chod and Lyandres (2020)
Revenue Sharing
\(q^{rs}<q^m\)
revenue sharing: underproduction
output presale: overproduction
\(c\)
\(MR\)
"does not internalize" = externality
address externality: TAX!
here: tax future token income
incremental token income gets shared
\(\Rightarrow\) combine the two to get the monopoly quantity!
Is token financing inferior?
Is token financing inferior? No!
- issue \(t\) tokens ex ante
- share \(\alpha_t\) of new tokens
- Entrepreneuer solves \[\max_q (1-\alpha_t) (q-t)(x-q) - cq\] solution \[q^t=(x+t-c/(1-\alpha_t))/2\]
- token share: \[\alpha_t=\frac{t}{c+t}\]
\(\alpha_tMR+t\)
\(q^t=q^m\)
Presell \(t\) tokens.
Collect enough funds to cover \(C_0\) + MC for the first \(t\) units.
As with equity, the entrepreneur receives the full NPV.
The entrepreneuer produces optimally at \(q^t=q^m\) (for any \(t\)).
If \(q^m<t\) \(\Rightarrow\) redeem at rate \(t/q\) and tokenholders receive refund of \(c(t-q)\).
If monopoly quantity \(q^m>t\), then share \(\alpha_t\) of revenue from incremental \(q^m-t\) tokens with tokenholders
Formal Result: Optimal Token Contract
- costs her \(0\)
- \(\theta\sim U(0,\theta_l)\)
- \(\theta_l<\theta_h\)
Idea:
entrepreneur can influence expected demand
- costs her \(C_e\)
- \(\theta\sim U(0,\theta_h)\)
with effort
without effort
common topic in corporate finance
very relevant in "decentralized" world where developers are scattered around the globe
also applicable to, e.g. established firms that do something new
assume \[\textit{NPV}(\text{effort})>0>\textit{NPV}(\text{no effort})\]
Token Issuance with Moral Hazard
Investors (equity or token holders) only finance the project if the entrepreneur undertakes the effort
Solve for the optimal funding conditional on the entrepreneur taking the effort
Derive conditions such that the entrepreneur undertakes effort
Financing with Moral Hazard
1.
2.
Equity Financing with Moral Hazard
equity holders
possibly break even
with effort
without effort
cannot break even
entrepreneur
earns \((1-\alpha_s)\ \frac{(\theta_h-c)^3}{12\theta_h} -C_e \)
with effort
without effort
earns \((1-\alpha_s) \frac{(\theta_l-c)^3}{12\theta_l}\)
\(>\) ?
exert effort iff
\[\textit{NPV}_h-C_e\ge \textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c}{\theta_h-c}\right)^3>0\]
demand \(\alpha_{s}\): \(\alpha_{s}\ \frac{(\theta_h-c)^3}{12\theta_h} =C_0 \)
Token Financing with Moral Hazard
token holders
possibly break even
with effort
without effort
cannot break even
entrepreneur
earns \(\frac{c}{c+t} \frac{2}{3\theta_h}\left(\frac{\theta_h-c}{2}-t \right)^3 -C_e \)
with effort
without effort
earns \(\frac{c}{c+t} \frac{2}{3\theta_l}\left(\frac{\theta_l-c}{2}-t \right)^3\)
\(>\) ?
exert effort iff
\[\textit{NPV}_h-C_e\ge \textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c-2t}{\theta_h-c-2t}\right)^3\]
Financing with Moral Hazard
key agebraic insight
\[\textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c}{\theta_h-c}\right)^3 >\textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c-2t}{\theta_h-c-2t}\right)^3\]
exert effort with equity financing iff
\[\textit{NPV}_h-C_e\ge \textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c}{\theta_h-c}\right)^3>0\]
exert effort with token financing iff
\[\textit{NPV}_h-C_e\ge \textit{NPV}_h\times\frac{\theta_h}{\theta_l}\left(\frac{\theta_l-c-2t}{\theta_h-c-2t}\right)^3\]
Key insight: a token contract incentivizes effort better than equity (similarly to canonical debt vs. equity insights)
Optimal token contract has debt features:
get nothing if demand is low (only original
tokenholders get anything)
benefit if demand is high
all projects that can be financed by equity can be financed by the optimal token contract but
Token Issuance with Moral Hazard
some projects that can be financed by optimal tokens contracts cannot be financed by equity.
Simple model of revenue-based ICO vs equity financing from the standard corporate finance + IO toolbox
Theorem 1: Without frictions, an optimal token contract finances the same
projects as equity
Theorem 2: With entrepreneurial moral hazard,
any equity-financeable project can be financed by an optimal token
some token-financeable projects cannot be financed by equity
\(\Rightarrow\) There is economic and conceptual merit to token financing
Summary
@katyamalinova
malinovk@mcmaster.ca

slides.com/kmalinova
sites.google.com/site/katyamalinova/