Computational Anatomy and PDE

Klas Modin

Outline

  1. Background
     
  2. EPDiff equation
     
  3. New gradient flow PDE

Background

Part 1

MR camera

CT scanner

Radiology or medical imaging is in the middle of a digital or computer revolution that is affecting all of science and its various fields, including medicine

– Nick Bryan, Radiological Society of North America

  • Better understanding of disease
  • Tool to facilitate diagnosis

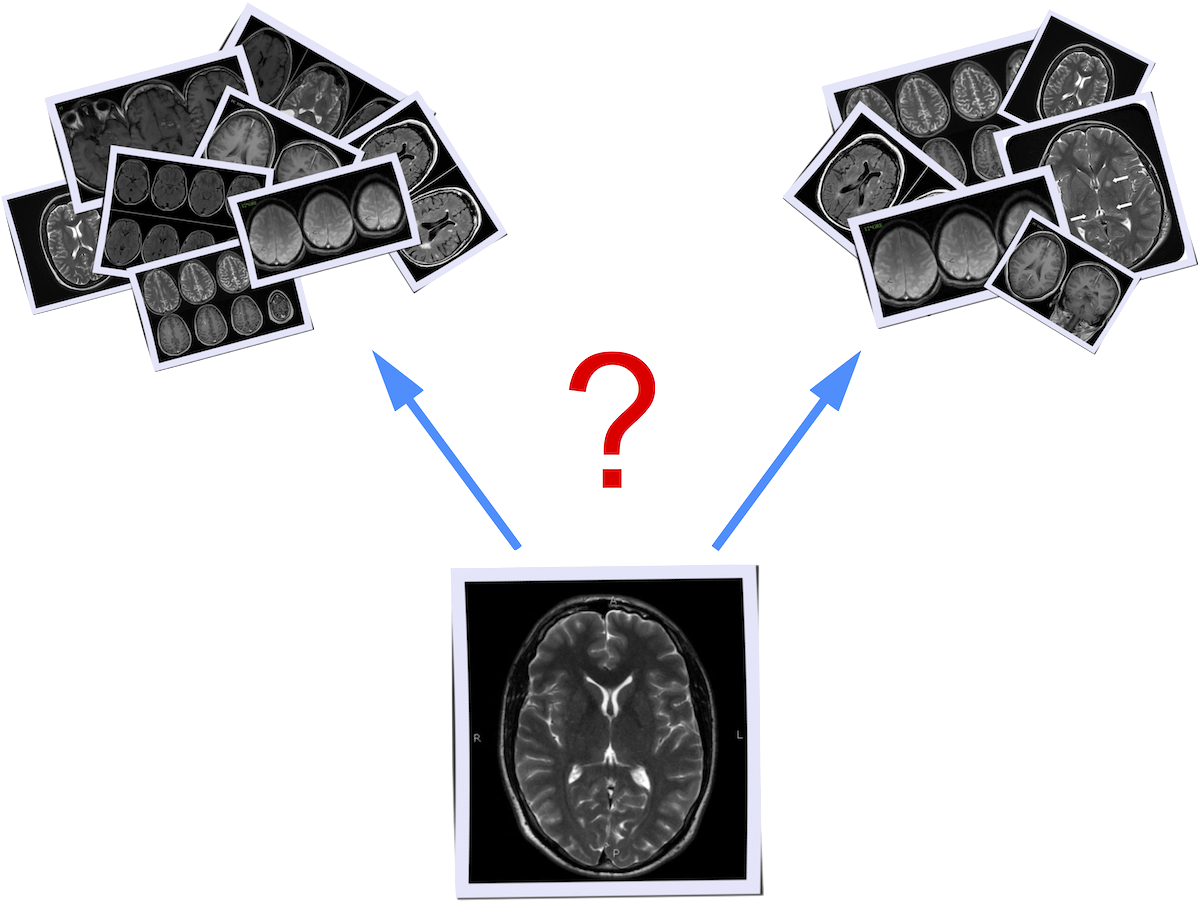
What is `distance` between images?

Riemannian geometry: distance in curved space

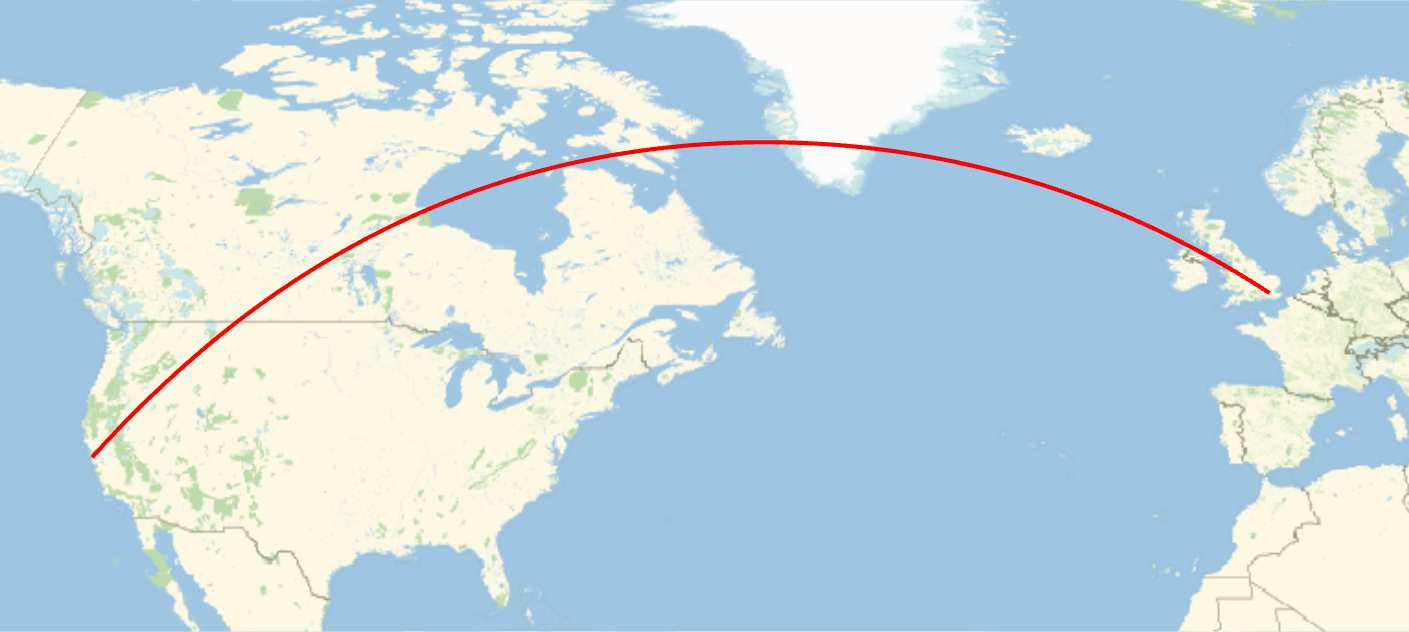
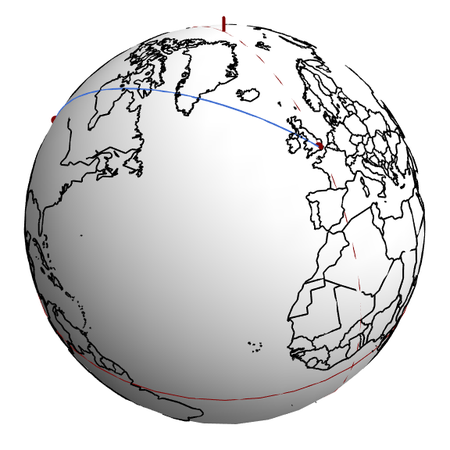
Exemple: great circles (2d)

Exemple: Einstein's space-time (4d)

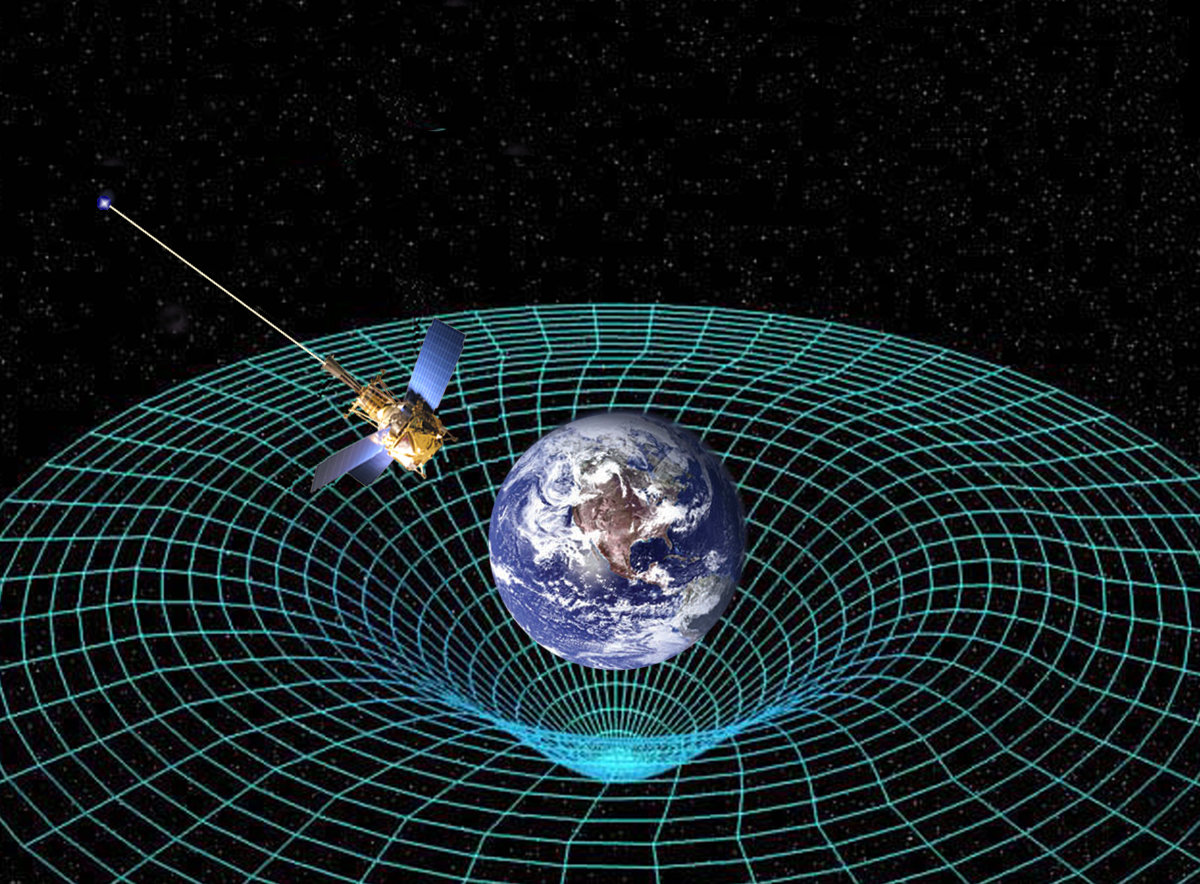
Exemple: space of diffeomorphisms (∞-dim)

\mathrm{Diff}(\Omega) = \{ \varphi\in C^{\infty}(\Omega,\Omega) \mid \varphi \text{ has smooth inverse}\}
Diff(Ω)={φ∈C∞(Ω,Ω)∣φ has smooth inverse}\mathrm{Diff}(\Omega) = \{ \varphi\in C^{\infty}(\Omega,\Omega) \mid \varphi \text{ has smooth inverse}\}

Image dist = Riemannian dist between \(\varphi\) and \(\mathrm{id}\)

What is computational anatomy?

  • Use Riemannian geometry on inf-dim manifold of diffeomorphisms to solve registration problems

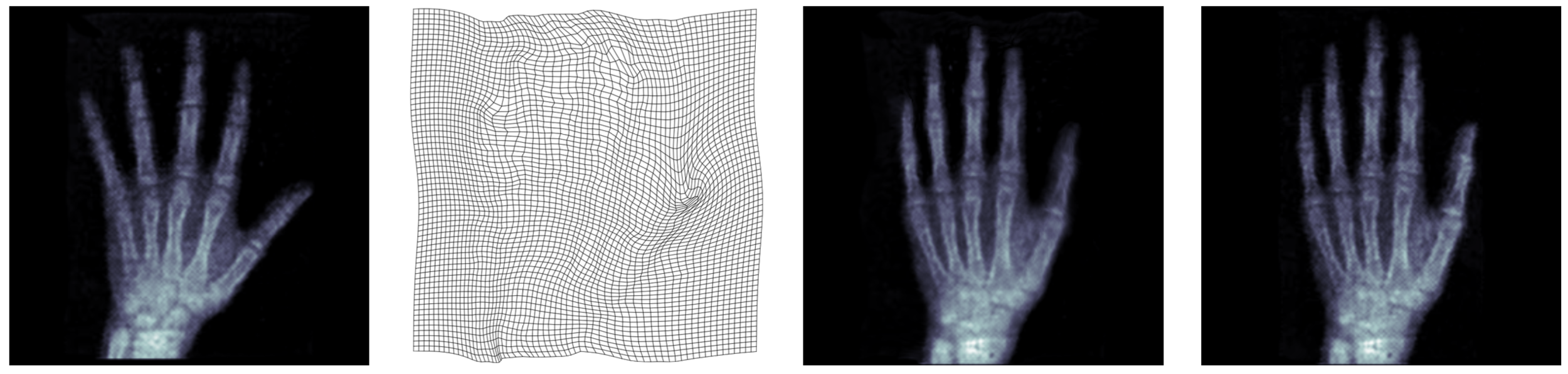
(a) Template

(b) Warp

(c) Transformed

(d) Target

History of computational anatomy

EPDiff equation

Part 2

Diffeomorphic image registration

  • Image domain \(\Omega\)
  • Template image \(I_0: \Omega \to \mathbb{R}_+ \)
  • Target image \(I_1:\Omega\to \mathbb{R}_+\)
\displaystyle\min_{\varphi\in\mathrm{Diff}(\Omega)}\lVert I_0\circ\varphi^{-1}-I_1 \rVert^2
min⁡φ∈Diff(Ω)∥I0∘φ−1−I1∥2\displaystyle\min_{\varphi\in\mathrm{Diff}(\Omega)}\lVert I_0\circ\varphi^{-1}-I_1 \rVert^2
\varphi
φ\varphi

Ill-posed with noise!

Large deformation diffeomorphic metric matching (LDDMM)

\displaystyle\min_{\varphi\in\mathrm{Diff}(\Omega)}\lVert I_0\circ\varphi^{-1}-I_1 \rVert^2 + \frac{1}{\sigma}\mathrm{dist}(\mathrm{id},\varphi)^2
min⁡φ∈Diff(Ω)∥I0∘φ−1−I1∥2+1σdist(id,φ)2\displaystyle\min_{\varphi\in\mathrm{Diff}(\Omega)}\lVert I_0\circ\varphi^{-1}-I_1 \rVert^2 + \frac{1}{\sigma}\mathrm{dist}(\mathrm{id},\varphi)^2
\displaystyle\mathrm{dist}(\mathrm{id},\varphi)^2 = \int_0^1 \lVert (1-\alpha \Delta)^k v(t) \rVert^2_{L^2} dt
dist(id,φ)2=∫01∥(1−αΔ)kv(t)∥L22dt\displaystyle\mathrm{dist}(\mathrm{id},\varphi)^2 = \int_0^1 \lVert (1-\alpha \Delta)^k v(t) \rVert^2_{L^2} dt
v(t) := \dot\varphi(t)\circ\varphi(t)^{-1} \quad \varphi(0)=\mathrm{id}, \varphi(1)=\varphi
v(t):=φ˙(t)∘φ(t)−1φ(0)=id,φ(1)=φv(t) := \dot\varphi(t)\circ\varphi(t)^{-1} \quad \varphi(0)=\mathrm{id}, \varphi(1)=\varphi
\displaystyle\min_{v\in C^\infty([0,1]\times\Omega,\mathbb{R}^n)}\lVert I_0\circ\varphi(1)^{-1}-I_1 \rVert^2 + \frac{1}{\sigma}\int_0^1 \lVert v(t,\cdot) \rVert^2_\mathcal{A} dt
min⁡v∈C∞([0,1]×Ω,Rn)∥I0∘φ(1)−1−I1∥2+1σ∫01∥v(t,⋅)∥A2dt\displaystyle\min_{v\in C^\infty([0,1]\times\Omega,\mathbb{R}^n)}\lVert I_0\circ\varphi(1)^{-1}-I_1 \rVert^2 + \frac{1}{\sigma}\int_0^1 \lVert v(t,\cdot) \rVert^2_\mathcal{A} dt
\frac{\partial}{\partial t}\varphi(t,\cdot) = v(t,\varphi(t,\cdot)), \quad \varphi(0,x) = x
∂∂tφ(t,⋅)=v(t,φ(t,⋅)),φ(0,x)=x\frac{\partial}{\partial t}\varphi(t,\cdot) = v(t,\varphi(t,\cdot)), \quad \varphi(0,x) = x

\(\varphi(1)\) related to \(v\) by

\lVert u \rVert_\mathcal{A} = \lVert \mathcal{A} u \rVert_{L^2} = \lVert (1-\alpha \Delta)^k u \rVert_{L^2}
∥u∥A=∥Au∥L2=∥(1−αΔ)ku∥L2\lVert u \rVert_\mathcal{A} = \lVert \mathcal{A} u \rVert_{L^2} = \lVert (1-\alpha \Delta)^k u \rVert_{L^2}

Norm \( || \cdot||_\mathcal{A} \) given by

Euler-Lagrange equations

\(\Longrightarrow\) EPDiff equation

  • Velocity \(v:[0,1]\times\Omega\to\mathbb{R}^n\)
  • Momentum \(m:[0,1]\times\Omega\to\mathbb{R}^n \)
\displaystyle\frac{\partial m}{\partial t} + \nabla m\cdot v + (\nabla v)^\top \cdot m + m(\nabla\cdot v) = 0
∂m∂t+∇m⋅v+(∇v)⊤⋅m+m(∇⋅v)=0\displaystyle\frac{\partial m}{\partial t} + \nabla m\cdot v + (\nabla v)^\top \cdot m + m(\nabla\cdot v) = 0
\displaystyle m = (1-\alpha\Delta)^k v
m=(1−αΔ)kv\displaystyle m = (1-\alpha\Delta)^k v

Numerical approach for LDDMM

  • Steepest descent over time-dependent vector fields
     
  • EPDiff IVP solver using particle methods (solitons)
     
  • Use shooting over initial velocity \(v_0\) to minimize
\displaystyle\lVert I_0\circ \varphi(1)^{-1}-I_1\rVert^2 + \frac{1}{\sigma}\lVert v_0 \rVert^2_\mathcal{A}
∥I0∘φ(1)−1−I1∥2+1σ∥v0∥A2\displaystyle\lVert I_0\circ \varphi(1)^{-1}-I_1\rVert^2 + \frac{1}{\sigma}\lVert v_0 \rVert^2_\mathcal{A}

Result: excellent! (but computationally expensive)

Open problems

  • Develop FE discretization for EPDiff IVP
  • Develop FE discretization for LDDMM
  • Adaptive FE
  • Numerical convergence analysis

*images by Matteo Molteni

New gradient flow PDE

Part 3

Deformation gradient flows

Right-invariant metric on \(\mathrm{Diff}(\Omega)\) defined by \(\mathcal A\)

Minimization problem

\displaystyle\min_{\varphi\in \mathrm{Diff}(\Omega)} \lVert(I_0\circ\varphi^{-1}-I_1\rVert^2
minφ∈Diff(Ω)∥(I0∘φ−1−I1∥2\displaystyle\min_{\varphi\in \mathrm{Diff}(\Omega)} \lVert(I_0\circ\varphi^{-1}-I_1\rVert^2
\displaystyle + \frac{1}{\sigma} d_{\text{FR}}(dx,\varphi_*dx)^2
+1σdFR(dx,φ∗dx)2\displaystyle + \frac{1}{\sigma} d_{\text{FR}}(dx,\varphi_*dx)^2

Origin of expensiveness: no formula for \(d_\mathrm{Diff}\)

\displaystyle + \frac{1}{\sigma} d_{\mathrm{Diff}}(\mathrm{id},\varphi)^2
+1σdDiff(id,φ)2\displaystyle + \frac{1}{\sigma} d_{\mathrm{Diff}}(\mathrm{id},\varphi)^2

Regularization penalizing change of volume

\(\mathrm{Diff}(\Omega)\) acts on \(Q = C^{\infty}(\Omega)\times \mathrm{Dens}(\Omega) \)

\( E(\varphi) = F_{q_1}(\varphi\cdot q_0)\) where \(q_i = (I_i,dx)\)

\dot \varphi = - \nabla_\mathcal{A} E(\varphi)
φ˙=−∇AE(φ)\dot \varphi = - \nabla_\mathcal{A} E(\varphi)
\mathrm{Diff}(\Omega)
Diff(Ω)\mathrm{Diff}(\Omega)
Q
QQ
\mathrm{id}
id\mathrm{id}
q_0
q0q_0
\varphi(t)
φ(t)\varphi(t)
q_1
q1q_1
q(t) = \varphi(t)\cdot q_0
q(t)=φ(t)⋅q0q(t) = \varphi(t)\cdot q_0
Q = C^{\infty}(\Omega)\times \mathrm{Dens}(\Omega)
Q=C∞(Ω)×Dens(Ω)Q = C^{\infty}(\Omega)\times \mathrm{Dens}(\Omega)
q_i = (I_i,dx)
qi=(Ii,dx)q_i = (I_i,dx)

Gradient flow is

 

 

 

 

 

 

\dot \varphi = - v(\varphi\cdot q_0)\circ \varphi
φ˙=−v(φ⋅q0)∘φ\dot \varphi = - v(\varphi\cdot q_0)\circ \varphi
(1-\alpha\Delta)^s v = \frac{1}{\sigma}\rho \nabla \rho + \nabla(I-I_\infty)
(1−αΔ)sv=1σρ∇ρ+∇(I−I∞)(1-\alpha\Delta)^s v = \frac{1}{\sigma}\rho \nabla \rho + \nabla(I-I_\infty)
\rho = \det(\varphi^{-1})
ρ=det(φ−1)\rho = \det(\varphi^{-1})
I = I_0\circ\varphi^{-1}
I=I0∘φ−1I = I_0\circ\varphi^{-1}

Lie-Euler method

 

 

 

 

 

\rho_k = \det(\varphi_k^{-1}) \quad I_k = I_0\circ\varphi_k^{-1}
ρk=det(φk−1)Ik=I0∘φk−1\rho_k = \det(\varphi_k^{-1}) \quad I_k = I_0\circ\varphi_k^{-1}
\varphi_{k+1} = \exp(-h v_k)\circ\varphi_k
φk+1=exp(−hvk)∘φk\varphi_{k+1} = \exp(-h v_k)\circ\varphi_k
(1-\alpha\Delta)^s v_k = \frac{1}{\sigma}\rho_k \nabla \rho_k + \nabla(I_k-I_\infty)
(1−αΔ)svk=1σρk∇ρk+∇(Ik−I∞)(1-\alpha\Delta)^s v_k = \frac{1}{\sigma}\rho_k \nabla \rho_k + \nabla(I_k-I_\infty)

Toy example (2D)

Open problem

  • Develop moving mesh FE discretization for gradient flow PDE

Course project

slides available at slides.com/kmodin/cmm-kristineberg