Zeitlin's model for ideal hydrodynamics on the sphere
(Part 1: numerical experiments)
Klas Modin


Collaborator: Milo Viviani

SNS Pisa

\dot\omega = \{\psi,\omega \}, \quad \Delta \psi = \omega
Euler's equations
\dot W = [P,W], \quad \Delta_N P = W
Zeitlin's model
W,P \in \mathfrak{su}(N)
azimuth
elevation
Smooth, randomly generated initial data
azimuth
elevation
Smooth, vanishing angular momentum initial data
azimuth
elevation
...run it faster
Questions:
- How exactly is Zeitlin's model related to Euler?
- How accurate is it?
- Does it capture the right dynamics?
- Can it give new insights?
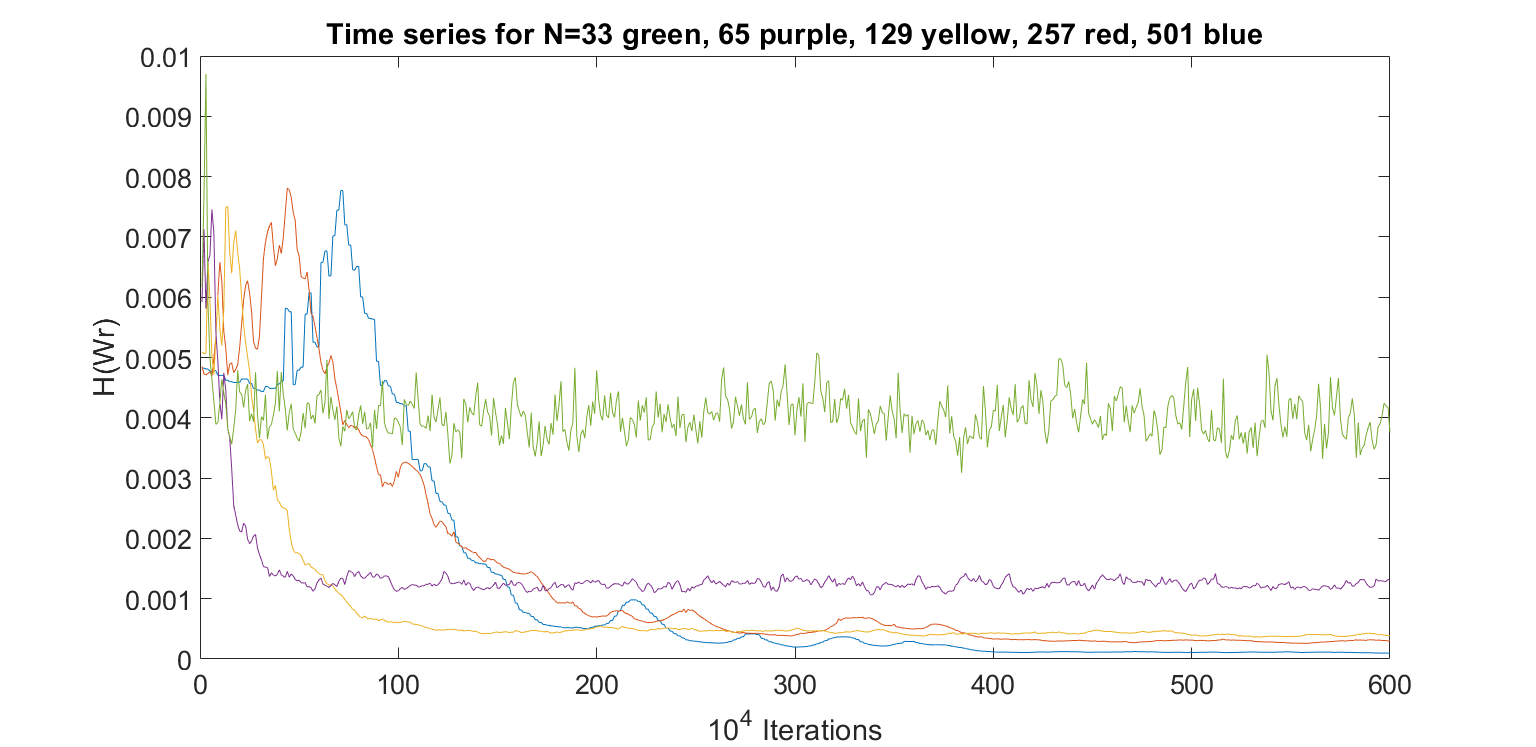
at fine scales: not at all!
...but no method is!
Example: canonical splitting
W = W_s + W_r \qquad (\omega = \omega_s + \omega_r)
W_s
W_r
projection onto stabilizer of \(P\)