Quaternions
(MMG640 / MVE080)
Overview
- Quaternion algebra
- Relation between unit quaternions and rotation matrices
- Euler's equations for rigid body motion
- Lie-Euler method
Quaternion algebra
Brief history: found by Hamilton in 1843 as a generalization of complex numbers


Multiplication rules:
Alternative notation
Pure quaternions: \[\mathcal{Q}_0 = \{q\mid q = (0,\underline{b}) \} \]
Unit quaternions: \[\mathcal{Q}_1 = \{q\mid q^cq = 1 \} \]
Conjugate: \[q^c = (a,-\underline{b})\]
Multiplication: \[q_1q_2 = (a_1a_2-\underline{b}_1\cdot\underline{b}_2,a_1\underline{b}_2 + a_2\underline{b}_1+\underline{b}_1\times\underline{b}_2)\]
Unit quaternions determine rotations
Let \(q=(\cos(\theta/2),\sin(\theta/2)\underline{b})\in\mathcal{Q}_1\) where \(|\underline{b}|=1\)
Then \(q\) corresponds to a rotation about the axis \(\underline{b}\) by the angle \(\theta\)
Notation: \(\mathrm{qexp}(\theta\underline{b}) = (\cos(\theta/2),\sin(\theta/2)\underline{b})\)
Let \(q= (a,\underline{b})\) be unitary. Then \(q\) determines a rotation matrix
Map \(\mathcal{R}_1\ni q\mapsto Q \in SO(3)\) is a double covering
Let \( \underline{\omega}\in\mathbb{R}^3\) and \(v = (0,\underline{\omega})\in\mathcal{Q}_0\)
Matrix multiplication \(R\underline{\omega}\) corresponds to \(qvq^{-1}\in\mathcal{Q}_0\)
Rigid body dynamics
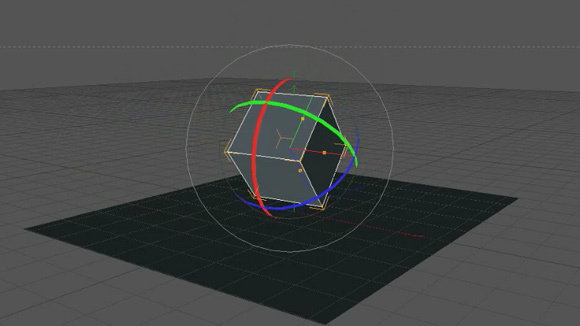
Orientation of rigid body described by \(R(t)\mathcal{B}\) for \(R(t)\in SO(3)\)
Body angular velocity \(\underline{\omega}(t) = R(t)^{-1}\dot R(t)\)
How does a rigid body move in space? Answer: according to Euler's equations
moments of inertia tensor
Lie-Euler method
Euler's equations
Matrix exponential (rotation about \(\underline{\omega}\) by angle \(|\underline{\omega}|\))
Lie-Euler time-stepping scheme