Riemannian Imaging

Klas Modin

Overview of

Outline

  • Motivation: image registration
  • Background: topological hydrodynamics
  • Shape matching
  • LDDMM (abstract)
  • Geometry of diffeomorphism group
  • EPDiff equation
  • Gradient flows on Lie groups
  • Toy example: gradient flow for \(QR\)
  • Gradient flows on diffeomorphisms
  • Examples

Image registration

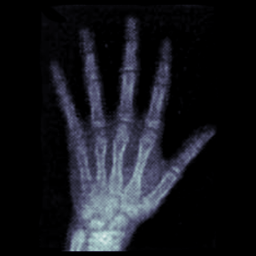
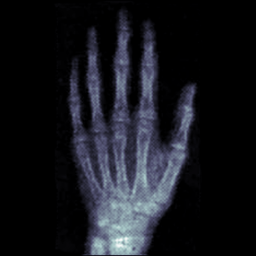
Find transformation warping \(I_0\) to \(I_1\)

I_0
I0I_0
I_1
I1I_1

Topological hydrodynamics

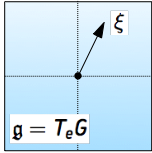
Geodesics on Lie group \(G\)

Right-invariant metric

defined by \(\mathcal A: \mathfrak{g}\to\mathfrak{g}^* \)

Euler-Poincaré equation

in variable \(\xi=g'\cdot g^{-1} \)

\[\mathcal A \xi'+\mathrm{ad}^*_\xi \mathcal A\xi = 0\]

Two examples

Rigid body

G=\mathrm{SO}(3), \quad \mathfrak{so}(3)\simeq \mathbb{R}^3
G=SO(3),so(3)≃R3G=\mathrm{SO}(3), \quad \mathfrak{so}(3)\simeq \mathbb{R}^3
\mathbb{I}\dot\omega + \mathbb{I}\omega\times\omega = 0
Iω˙+Iω×ω=0\mathbb{I}\dot\omega + \mathbb{I}\omega\times\omega = 0

Incompressible Euler equations

G=\mathrm{Diff}_\mu(M), \quad \mathfrak{g} = \mathfrak{X}_\mu(M)
G=Diffμ(M),g=Xμ(M)G=\mathrm{Diff}_\mu(M), \quad \mathfrak{g} = \mathfrak{X}_\mu(M)
\dot v + \nabla_v v = -\nabla p
v˙+∇vv=−∇p\dot v + \nabla_v v = -\nabla p

Shape matching

Lie group \(G\) with left action on manifold \(Q\)

Minimization problem

\displaystyle\min_{g\in G} F_{q_1}(g\cdot q_0)
ming∈GFq1(g⋅q0)\displaystyle\min_{g\in G} F_{q_1}(g\cdot q_0)
+ \sigma R(g)
+σR(g)+ \sigma R(g)
g
gg
q_0
q0q_0
q_1
q1q_1

LDDMM framework

Right-invariant metric on \(G\) defined by \(\mathcal A: \mathfrak{g}\to \mathfrak{g}^*\)

Distance function \(d_Q\) on \(Q\)

Minimization problem

\displaystyle\min_{g\in G} d_Q^2(g\cdot q_0,q_1) + \sigma d_G^2(g,e)
ming∈GdQ2(g⋅q0,q1)+σdG2(g,e)\displaystyle\min_{g\in G} d_Q^2(g\cdot q_0,q_1) + \sigma d_G^2(g,e)

(Large Deformation Diffeomorphic Metric Matching)

Reformulation as curve on \(\mathfrak{g}\)

\displaystyle\min_{\xi\in C^\infty([0,1],\mathfrak{g})} d_Q^2(g(1)\cdot q_0,q_1) + \sigma \int_0^1 |\xi(t)|_{\mathcal{A}}^2 dt
minξ∈C∞([0,1],g)dQ2(g(1)⋅q0,q1)+σ∫01∣ξ(t)∣A2dt\displaystyle\min_{\xi\in C^\infty([0,1],\mathfrak{g})} d_Q^2(g(1)\cdot q_0,q_1) + \sigma \int_0^1 |\xi(t)|_{\mathcal{A}}^2 dt
\dot g = \xi \cdot g
g˙=ξ⋅g\dot g = \xi \cdot g
\displaystyle\min_{\xi\in L^2([0,1],\mathfrak{g})} d_Q^2(g(1)\cdot q_0,q_1) + \sigma \int_0^1 |\xi(t)|_{\mathcal{A}}^2 dt
minξ∈L2([0,1],g)dQ2(g(1)⋅q0,q1)+σ∫01∣ξ(t)∣A2dt\displaystyle\min_{\xi\in L^2([0,1],\mathfrak{g})} d_Q^2(g(1)\cdot q_0,q_1) + \sigma \int_0^1 |\xi(t)|_{\mathcal{A}}^2 dt

Lemma:

Minimizer \(\xi(t)\) fulfills the Euler-Poincaré equation

Proof:

L(g,\dot g) = \langle \mathcal A\dot g\cdot g^{-1},\dot g\cdot g^{-1}\rangle = |\xi|_\mathcal A^2
L(g,g˙)=⟨Ag˙⋅g−1,g˙⋅g−1⟩=∣ξ∣A2L(g,\dot g) = \langle \mathcal A\dot g\cdot g^{-1},\dot g\cdot g^{-1}\rangle = |\xi|_\mathcal A^2

Riemannian geometry of diffeomorphisms

G=\mathrm{Diff}(M), \quad \mathfrak{g} = \mathfrak{X}(M)
G=Diff(M),g=X(M)G=\mathrm{Diff}(M), \quad \mathfrak{g} = \mathfrak{X}(M)
\displaystyle\langle \mathcal A v, v\rangle = \int_M \mathsf{g}((1-\alpha\Delta)^k v, v) \mu
⟨Av,v⟩=∫Mg((1−αΔ)kv,v)μ\displaystyle\langle \mathcal A v, v\rangle = \int_M \mathsf{g}((1-\alpha\Delta)^k v, v) \mu
\dot m + \nabla_v m + m\, \mathrm{div}(v) + (\nabla v)^\top m = 0
m˙+∇vm+mdiv(v)+(∇v)⊤m=0\dot m + \nabla_v m + m\, \mathrm{div}(v) + (\nabla v)^\top m = 0
m = (1-\Delta)^k v
m=(1−Δ)kv m = (1-\Delta)^k v

Numerics for LDDMM

Approach 1

Gradient flow on curve \(v = v(t)\)

Approach 2

Geodesic shooting to minimize \(d_Q^2(\varphi(1)\cdot q_0,q_1)\)

Both are expensive!

Deformation gradient flows

Right-invariant metric on \(G\) defined by \(\mathcal A: \mathfrak{g}\to \mathfrak{g}^*\)

Distance function \(d_S\) on \(S\)

Minimization problem

\displaystyle\min_{g\in G} d_S^2(g\cdot s_0,s_1)
ming∈GdS2(g⋅s0,s1)\displaystyle\min_{g\in G} d_S^2(g\cdot s_0,s_1)
+ \sigma d_G^2(g,e)
+σdG2(g,e)+ \sigma d_G^2(g,e)

Origin of expensiveness: no formula for \(d_G\)

+ \sigma d_R^2(g\cdot r,r)
+σdR2(g⋅r,r)+ \sigma d_R^2(g\cdot r,r)

Regularization element \(r\in R\)

\(G\) acts on \(Q = S\times R \)

\( E(g) = F_{q_1}(g\cdot q_0)\) where \(q_i = (s_i,r)\)

\dot g = - \nabla_\mathcal{A} E(g)
g˙=−∇AE(g)\dot g = - \nabla_\mathcal{A} E(g)

Def: momentum map \(J: T^*Q\to \mathfrak{g}^* \) for cotangent lifted action

 

 

\langle J(q,p),\xi \rangle = \langle p,\xi\cdot q \rangle
⟨J(q,p),ξ⟩=⟨p,ξ⋅q⟩\langle J(q,p),\xi \rangle = \langle p,\xi\cdot q \rangle

Proposition: gradient flow is

 

 

 

 

\dot g = - u(g\cdot q_0)\cdot g
g˙=−u(g⋅q0)⋅g\dot g = - u(g\cdot q_0)\cdot g
u(q) = \mathcal A^{-1}J(q,d F_{q_1}(q))
u(q)=A−1J(q,dFq1(q))u(q) = \mathcal A^{-1}J(q,d F_{q_1}(q))
G
GG
Q
QQ
e
ee
q_0
q0q_0
g(t)
g(t)g(t)
q_1
q1q_1
q(t) = g(t)\cdot q_0
q(t)=g(t)⋅q0q(t) = g(t)\cdot q_0

Gradient flow

 

 

 

\dot g = - u(g\cdot q_0)\cdot g
g˙=−u(g⋅q0)⋅g\dot g = - u(g\cdot q_0)\cdot g
u(q) = \mathcal A^{-1}J(q,F_{q_*}(q))
u(q)=A−1J(q,Fq∗(q))u(q) = \mathcal A^{-1}J(q,F_{q_*}(q))

Lie-Euler method

 

 

 

 

 

q_k = g_k\cdot q_0
qk=gk⋅q0q_k = g_k\cdot q_0
\xi_k = \mathcal{A}^{-1}J(q_k,d F_{q_*})
ξk=A−1J(qk,dFq∗)\xi_k = \mathcal{A}^{-1}J(q_k,d F_{q_*})
g_{k+1} = \exp(-h\xi_k)g_k
gk+1=exp(−hξk)gkg_{k+1} = \exp(-h\xi_k)g_k

horizontal slice

I
II
R
RR

fiber

\pi
π\pi

fiber

I
II
W_1
W1W_1
K
KK
P(n)
P(n)P(n)
A
AA
Q
QQ

Toy example: \(QR\) factorization

\mathrm{Hor}_A = \{ V\in T_A\mathrm{GL}(n) \mid \ell(VA^{-1}) = 0 \}
HorA={V∈TAGL(n)∣ℓ(VA−1)=0}\mathrm{Hor}_A = \{ V\in T_A\mathrm{GL}(n) \mid \ell(VA^{-1}) = 0 \}
K = \{ R\in \mathrm{GL}(n)\mid \ell(R)=0, R_{ii}>0 \} \Rightarrow T_R K = \mathrm{Hor}_R
K={R∈GL(n)∣ℓ(R)=0,Rii>0}⇒TRK=HorRK = \{ R\in \mathrm{GL}(n)\mid \ell(R)=0, R_{ii}>0 \} \Rightarrow T_R K = \mathrm{Hor}_R

Take \(G = \mathrm{GL}(n)\) and \(Q = P(n)\)

Relative entropy as functional

F_{W_1}(W) = \frac{n}{2}- \frac{1}{2}\mathrm{tr}(W_1W^{-1}) + \frac{1}{2}\log(\det(W_1W^{-1}))
FW1(W)=n2−12tr(W1W−1)+12log(det(W1W−1))F_{W_1}(W) = \frac{n}{2}- \frac{1}{2}\mathrm{tr}(W_1W^{-1}) + \frac{1}{2}\log(\det(W_1W^{-1}))
\displaystyle \dot R = \nabla_{\mathcal A} E(R), \qquad E(R) = H(I\cdot R) = H(R^\top R)
R˙=∇AE(R),E(R)=H(I⋅R)=H(R⊤R)\displaystyle \dot R = \nabla_{\mathcal A} E(R), \qquad E(R) = H(I\cdot R) = H(R^\top R)
\displaystyle \dot R = \frac{1}{2} R^{-\top}(W_1-R^\top R) + ZR, \qquad Z\in\mathfrak{o}(n)
R˙=12R−⊤(W1−R⊤R)+ZR,Z∈o(n)\displaystyle \dot R = \frac{1}{2} R^{-\top}(W_1-R^\top R) + ZR, \qquad Z\in\mathfrak{o}(n)
R = \begin{bmatrix} 3 & -1 \\ 0 & 2 \end{bmatrix}
R=[3−102]R = \begin{bmatrix} 3 & -1 \\ 0 & 2 \end{bmatrix}
W_1 = \pi(R) = R^\top R
W1=π(R)=R⊤RW_1 = \pi(R) = R^\top R

Inf-dim example

  • \(G=\mathrm{Diff}(M)\)
  • \(Q = \mathrm{Dens}(M)\times \mathrm{Met}(M)\)
  • Action of \(G\) on \(Q\)
\varphi\cdot (\mu,\mathsf{g}) = (\varphi_*\mu, \varphi_*\mathsf{g})
φ⋅(μ,g)=(φ∗μ,φ∗g)\varphi\cdot (\mu,\mathsf{g}) = (\varphi_*\mu, \varphi_*\mathsf{g})
  • Right-invariant metric: \(H^1\)
  • Energy functional
E(\varphi) = d^2_{FR}(\varphi_*\mu_0,\mu_1) + \sigma d_{\text{Met}}^2(\varphi_*\mathsf{g},\mathsf{g})
E(φ)=dFR2(φ∗μ0,μ1)+σdMet2(φ∗g,g)E(\varphi) = d^2_{FR}(\varphi_*\mu_0,\mu_1) + \sigma d_{\text{Met}}^2(\varphi_*\mathsf{g},\mathsf{g})