A Silly Method for
QR Factorization
Klas Modin

Outline
- Riemannian geometry
- Manifold of multivariate Gaussians
- Fisher-Rao metric
- Homogeneous space structure
- QR (and Cholesky)
- Gradient flow
- Convexity and convergence
- Numerical example
Manifold
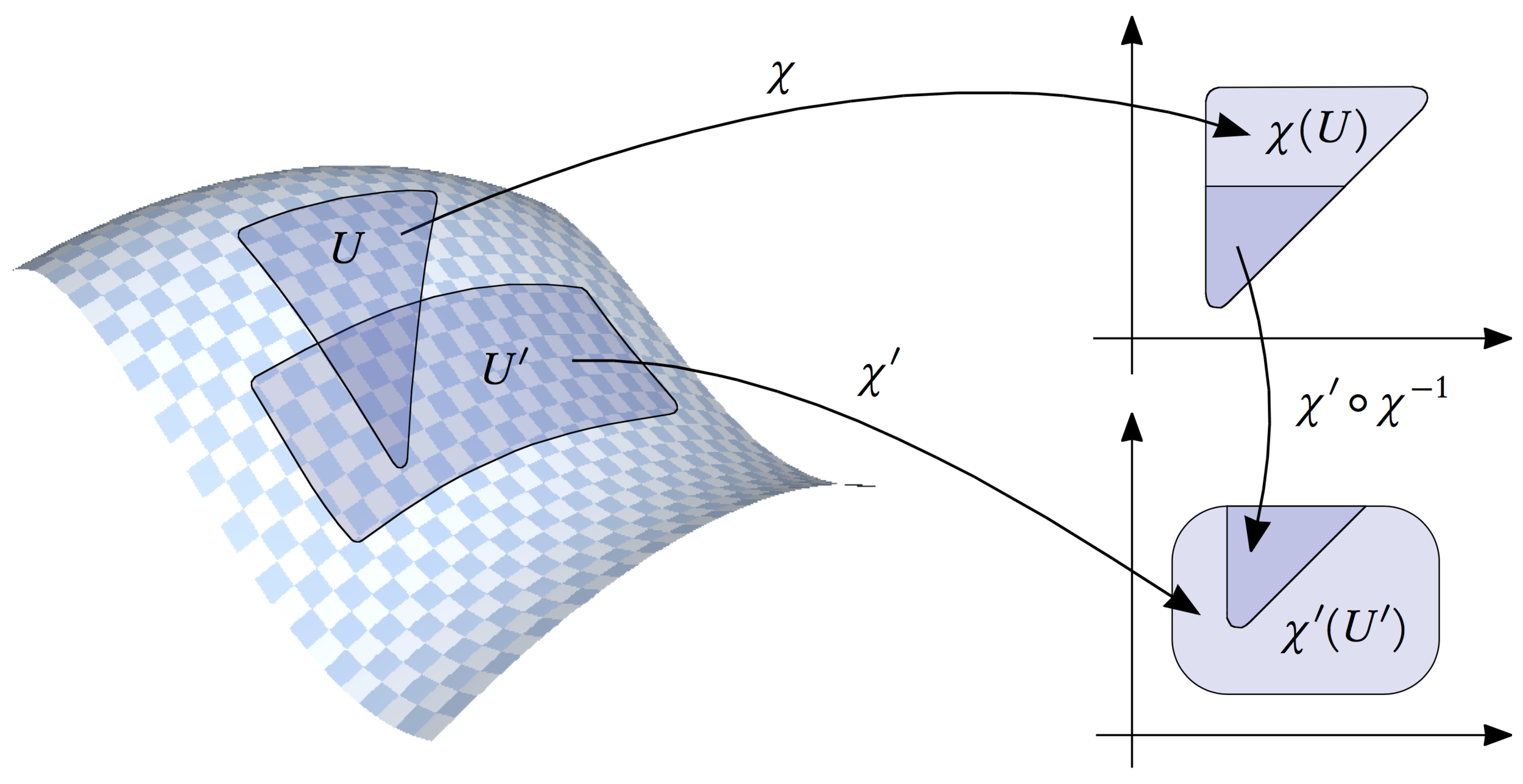
Riemannian manifold
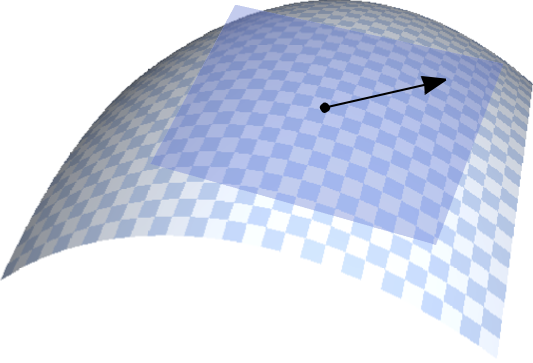
v
g_x(v,v) = \langle v,v\rangle_x
\displaystyle L(\gamma) = \int_0^1 \sqrt{g_{\gamma(s)}\big(\gamma'(s),\gamma'(s)\big)}\mathrm{d}t
x
\displaystyle A(\gamma) = \int_0^1 g_{\gamma(s)}\big(\gamma'(s),\gamma'(s)\big)\mathrm{d}t
Information geometry


\displaystyle p(x;\mu,\Sigma) = \frac{1}{\sqrt{(2\pi)^n|\Sigma|}}\exp(-\frac{1}{2}(x-\mu)^\top \Sigma^{-1}(x-\mu))
[Amari, ~80's]
Information geometry


\displaystyle p(x;\Sigma) = \frac{1}{\sqrt{(2\pi)^n|\Sigma|}}\exp(-\frac{1}{2}x^\top \Sigma^{-1}x)
[Amari, ~80's]
Manifold of inverse covariance matrices
P(n) = \{ W\in \mathbb{R}^{n\times n}\mid W=W^\top, W>0 \}

\displaystyle p(x;W^{-1}) = \sqrt{\frac{|W|}{(2\pi)^n}}\exp(-\frac{1}{2}x^\top W x)
Fisher-Rao metric on P(n)
T_W P(n) = \{ U\in \mathbb{R}^{n\times n}\mid U=U^\top \}
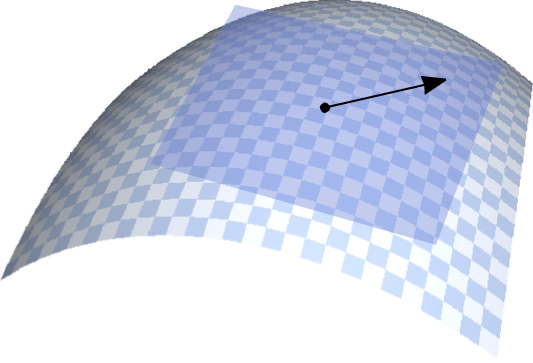
U
W
g_W(U,U) = \frac{1}{2}\mathrm{tr}(W^{-1}UW^{-1}U)
Geodesics on P(n)

\ddot W - \dot W W^{-1}\dot W = 0
Explicit distance function
\displaystyle d(W_0,W_1)^2 = \frac{1}{2}\mathrm{tr}\big(\log(W_1W_0^{-1})\log(W_1W_0^{-1}) \big)
Geodesic equation
W_0
W_1
Where is QR?!
Homogeneous space structure
I
fiber
\pi
fiber
I
W_1
P(n)
A
Q
\mathrm{GL}(n)
\mathrm{O}(n)\backslash \mathrm{GL}(n) = \{ [A] \mid A\in\mathrm{GL}(n), [A]=\mathrm{O}(n)\cdot A \}
\mathrm{O}(n)\backslash \mathrm{GL}(n) \simeq P(n) \quad\text{by}\quad \pi\colon A\mapsto A^\top A
Principal bundle
Fisher-Rao invariance

U
W
g_W(U,U) = \frac{1}{2}\mathrm{tr}(W^{-1}UW^{-1}U)
\mathrm{GL}(n)\times P(n) \ni (A,W) \mapsto A^\top W A \in P(n)
Right action of GL(n) on P(n)
g_{A^\top W A}(A^\top U A,A^\top U A) = g_W(U,U)
Compatible metric on GL(n)
\displaystyle \bar g_A(V,V) = \frac{1}{2}\mathrm{tr}\big(\ell(VA^{-1})^\top\ell(VA^{-1})+\sigma(VA^{-1})\sigma(VA^{-1}) \big)

V
A
horizontal slice
I
R
fiber
\pi
fiber
I
W_1
K
P(n)
A
Q
Horizontal distribution
\mathrm{Hor}_A = \{ V\in T_A\mathrm{GL}(n) \mid \ell(VA^{-1}) = 0 \}
K = \{ R\in \mathrm{GL}(n)\mid \ell(R)=0, R_{ii}>0 \} \Rightarrow T_R K = \mathrm{Hor}_R
horizontal slice
I
R
fiber
\pi
fiber
I
W_1
K
P(n)
A
Q
QR and Cholesky in one go
Voilà!
horizontal slice
I
R
I
W_1
A
Lifted gradient flow
K
\mathrm{P}(n)
- Convex functional on with
- Lifted functional on
- Consider gradient flow on horizontal slice
F
\mathrm{P}(n)
\nabla_{g}F(W_1) = 0
\mathrm{GL}(n)
\bar F(A) = F(\pi(A)) = F(A^\top A)
\dot R = -\nabla_{\bar g} \bar F(R)
Use relative entropy
H(W) = \frac{n}{2}- \frac{1}{2}\mathrm{tr}(W_1W^{-1}) + \frac{1}{2}\log(\det(W_1W^{-1}))
\displaystyle \dot R = \nabla_{\bar g}\bar H(R), \qquad \bar H(R) = H(R^\top R)
Final gradient flow
\displaystyle \dot R = \frac{1}{2} R^{-\top}(W_1-R^\top R) + ZR, \qquad Z\in\mathfrak{o}(n)
Use your favorite Runge-Kutta method!
That is, use RK4
Convergence
Convexity lemma:
-\mathrm{Hess}(\bar H)_R = \bar g_R
Corollary:
\bar d^2(R(t),R_\infty) \leq \, \mathrm{e}^{-2 t} \bar d^2(R(0),R_\infty)
R = \begin{bmatrix}
3 & -1 \\
0 & 2
\end{bmatrix}

W_1 = \pi(R) = R^\top R
Example
Example
-\bar H(R(t))

\bar d(R(t),R_\infty)^2
\text{slope of }\exp(-2t)