Symplectic integrators for classical spin systems
Klas Modin


Joint work with
Robert McLachlan
Massey University
Olivier Verdier
Western Norway University


Outline
- Symplectic integrators on \(\mathbb{R}^{2n}\)
- Slightly dissipative systems
- Spherical midpoint method
Illustration
- Non-linear pendulum \(H(q,p) = p^2/2 -\cos(q)\)
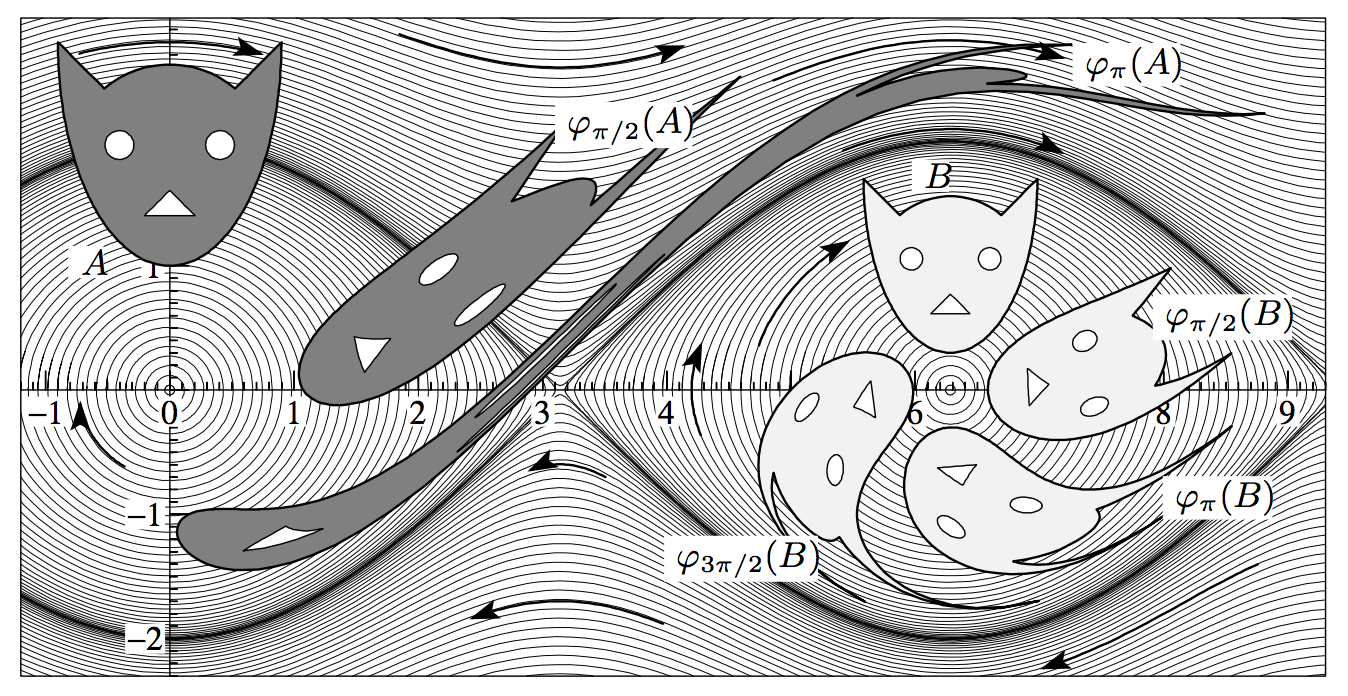
Illustration
- Non-linear pendulum \(H(q,p) = p^2/2 -\cos(q)\)
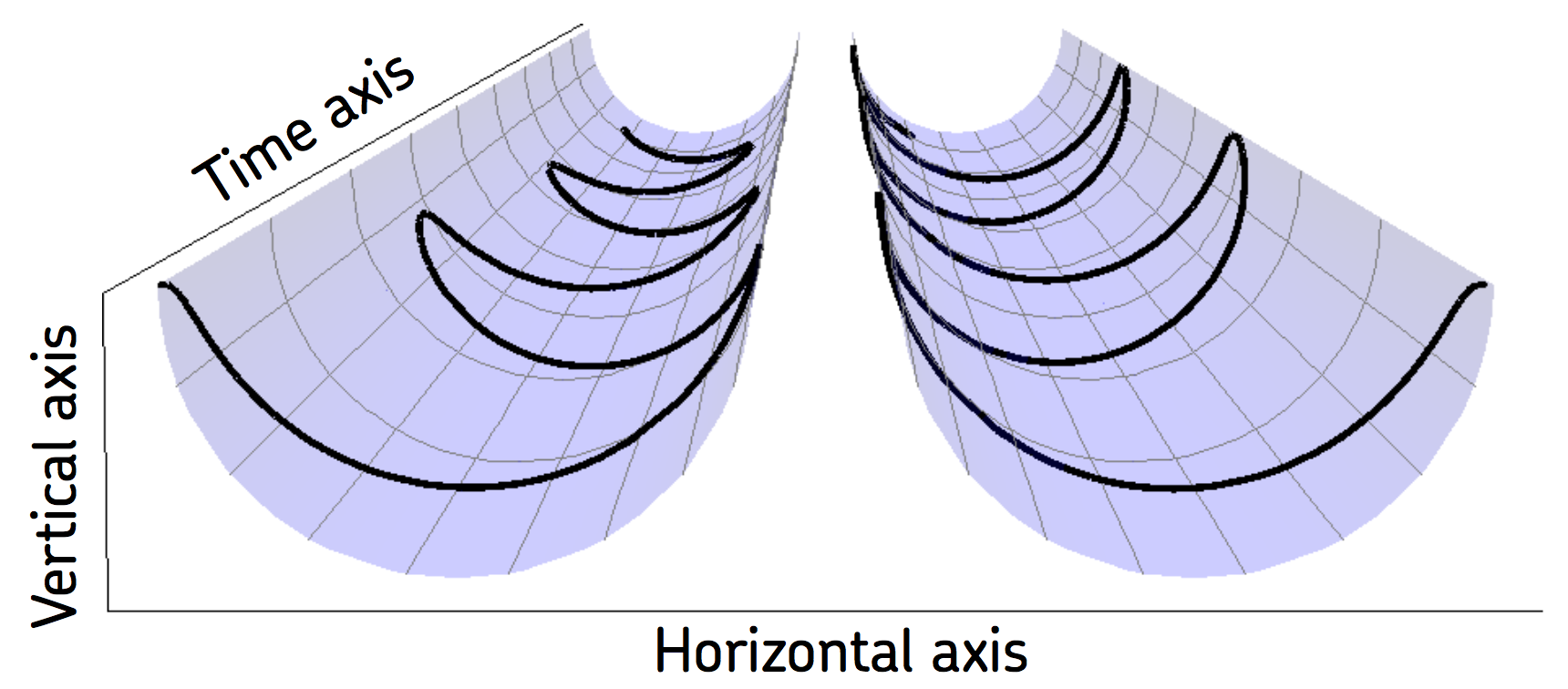
Illustration
- Non-linear pendulum \(H(q,p) = p^2/2 -\cos(q)\)
Why?
Hamiltonian dynamics on co-tangent bundles
Phase space \(T^*Q\)
Simplest case \(T^*\mathbb{R}^n\simeq \mathbb{R}^{2n}\)
Typical examples: celestial mechanics, molecular dynamics
Symplectic property of the flow
Symplectic 2-form:
On \(\mathbb{R}^{2n}\):
Hamiltonian vector fields fulfill (defining property)
Flow \(\varphi_t\) preserves the symplectic form:
Geometric interpretation: the "symplectic area" of 2D surfaces in phase space are preserved
Consequences of symplecticness
This explains why symplectic integrators are superior!
- "Almost" conservation of tori for Hamiltonian perturbations of integrable systems (KAM theory)
- Convergence towards correct macroscopic equilibrium (e.g. temperature in MD)
Common symplectic integrators on \(\mathbb{R}^{2n}\)
- Verlet scheme (many names: Leap-frog, Störmer-Verlet, symmetric splitting, Strang splitting, etc) for \(H(q,p) = T(p) + V(q)\)
- Midpoint method
Slightly dissipative systems
- Elastic 3D pendulum
Slightly dissipative systems
- Elastic 3D pendulum
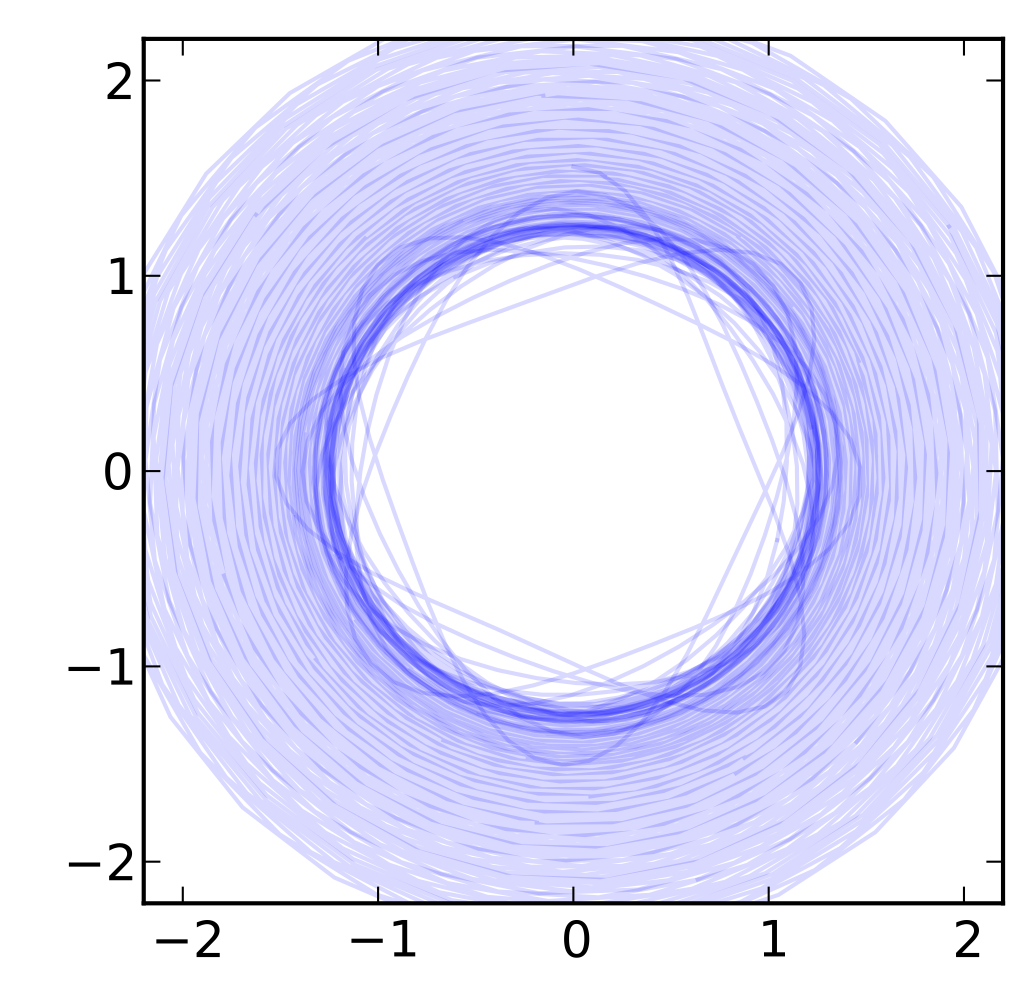
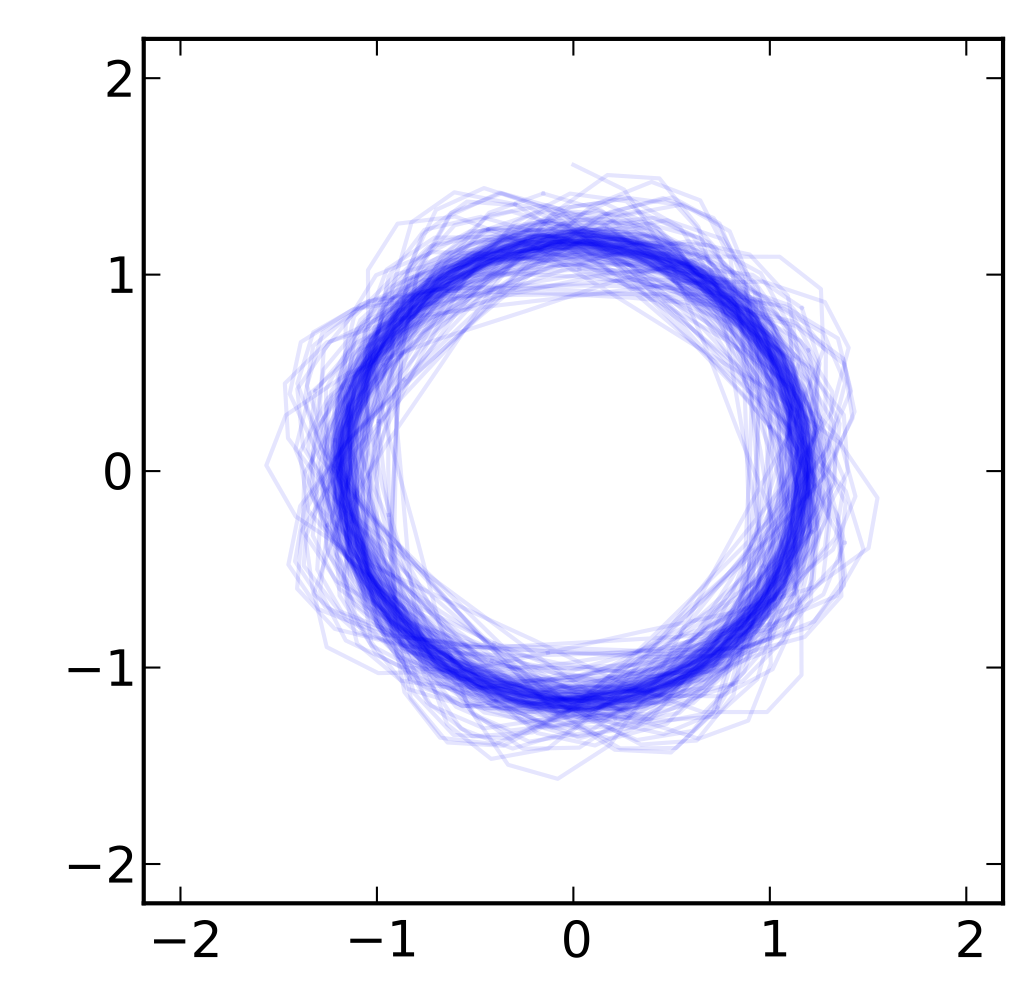
non-symplectic
symplectic
Slightly dissipative systems
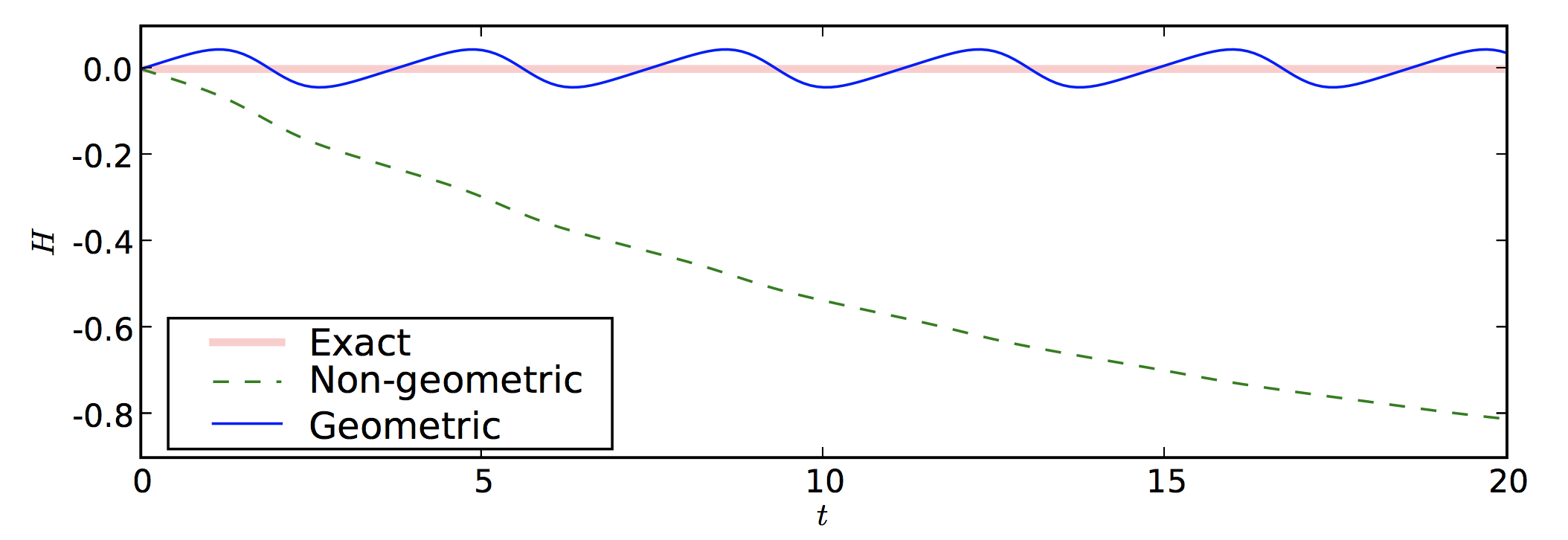
- Elastic 3D pendulum
Energy behaviour
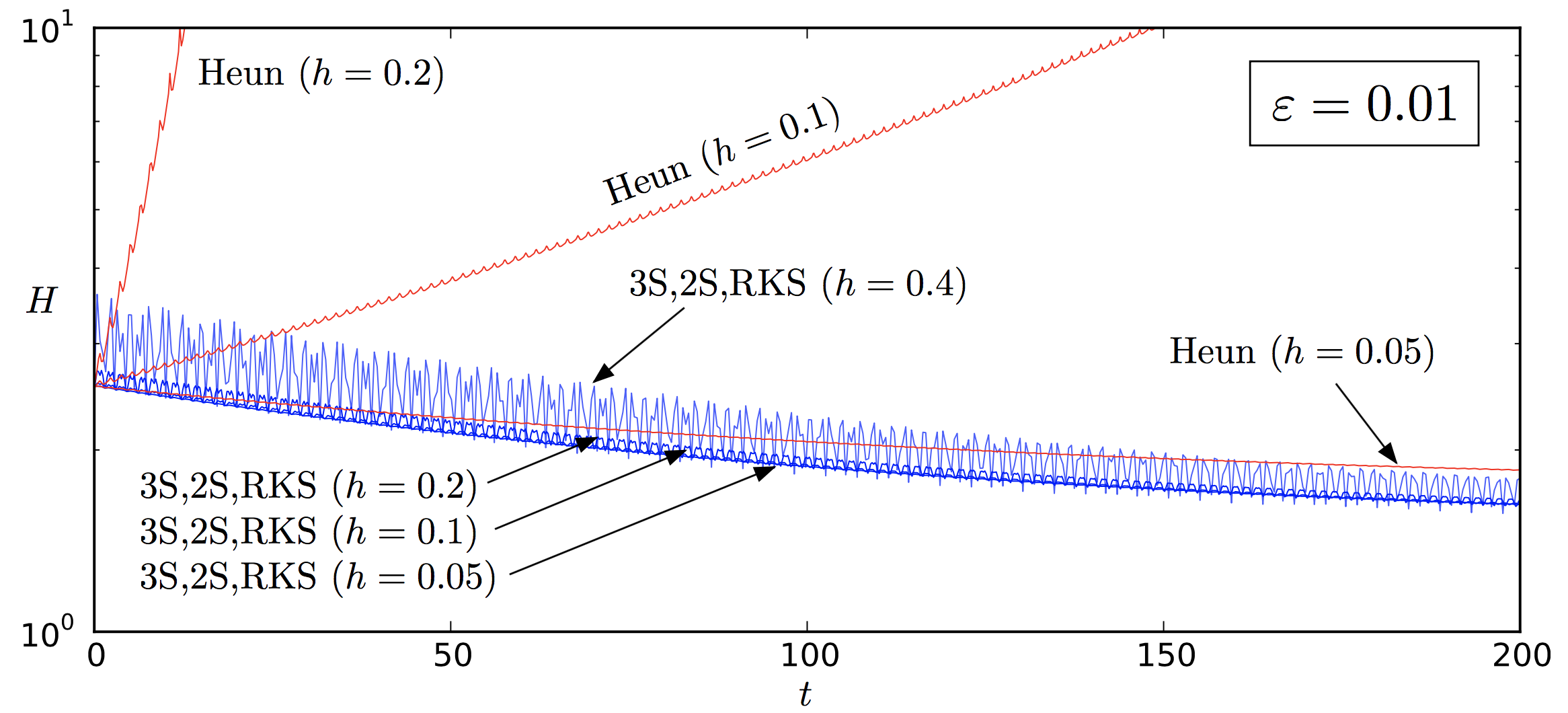
Classical spin systems
Phase space \((S^2)^n\)

Symplectic structure on \(S^2\) \[\Omega_w(u,v)=\mathrm{det}(w,u,v)\]

Motivation for spin systems
-
Abundance in physics
(e.g. atomistic spin dynamics)
-
Simplest Kähler manifold
-
Simplest coadjoint orbit
-
Simplest inexact symplectic form
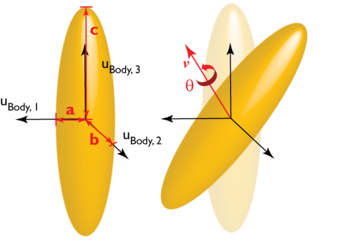
Some example spin systems
Free rigid body \[\dot w = w\times I^{-1}w \]
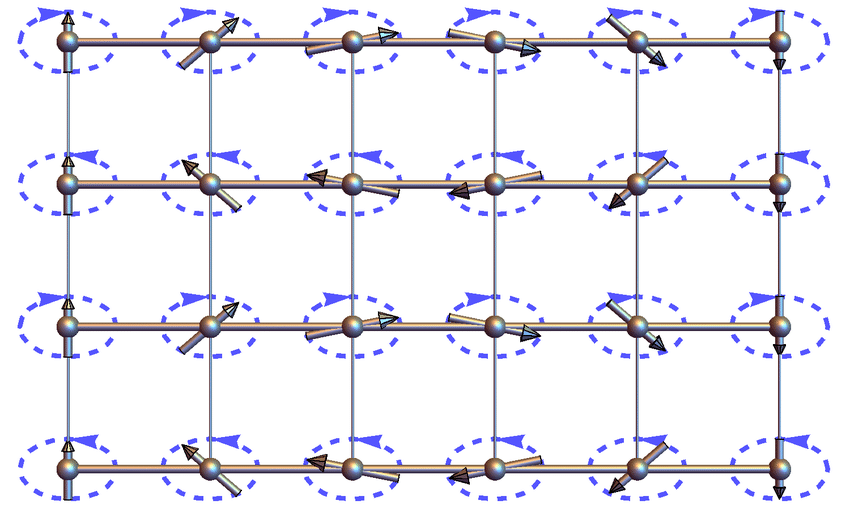
Heisenberg spin chain
(discrete Landau-Lifshitz) \[\dot w_i = w_i\times (w_{i-1}+w_{i+1}) \]
Fluid particle tracking on sphere \[\dot w = \xi(t,w), \quad \xi(t,\cdot)\in \mathfrak{X}_\mu(S^2) \]
Point vortex dynamics on spheres
(Jupiter's great red spot)

Known symplectic integrators
- Splitting methods
- \(S^2\) coadjoint orbit of reduced system on \(T^*SU(2) \)
RATTLE \(\Rightarrow\) 9 variables
Variational Lie \(\Rightarrow\) 8 variables
- Collective symplectic integrator
\(\Rightarrow\) 4 variables

Drawbacks: many auxiliary variables, complicated, large error constants
Minimum variables (=3)
and symplectic?
- Classical midpoint method on \(\mathbb{R}^3\)
- Riemannian midpoint method on \(S^2\)
\(\Rightarrow\) not symplectic
\(\Rightarrow\) not symplectic
Candidates:
Spherical midpoint method
Main result
- Second order
- Equivariant w.r.t. \(SO(3)^n\)
- Symplectic
- Preserves single-spin quadratic invariants
- Self-adjoint
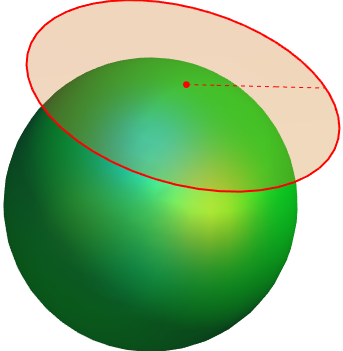
Hopf fibration
Extended Hopf fibration
Classical
midpoint
Riemannian
midpoint
Simple interpretation
Classical midpoint method applied to \(\bar X_H\)
Example 1: free rigid body

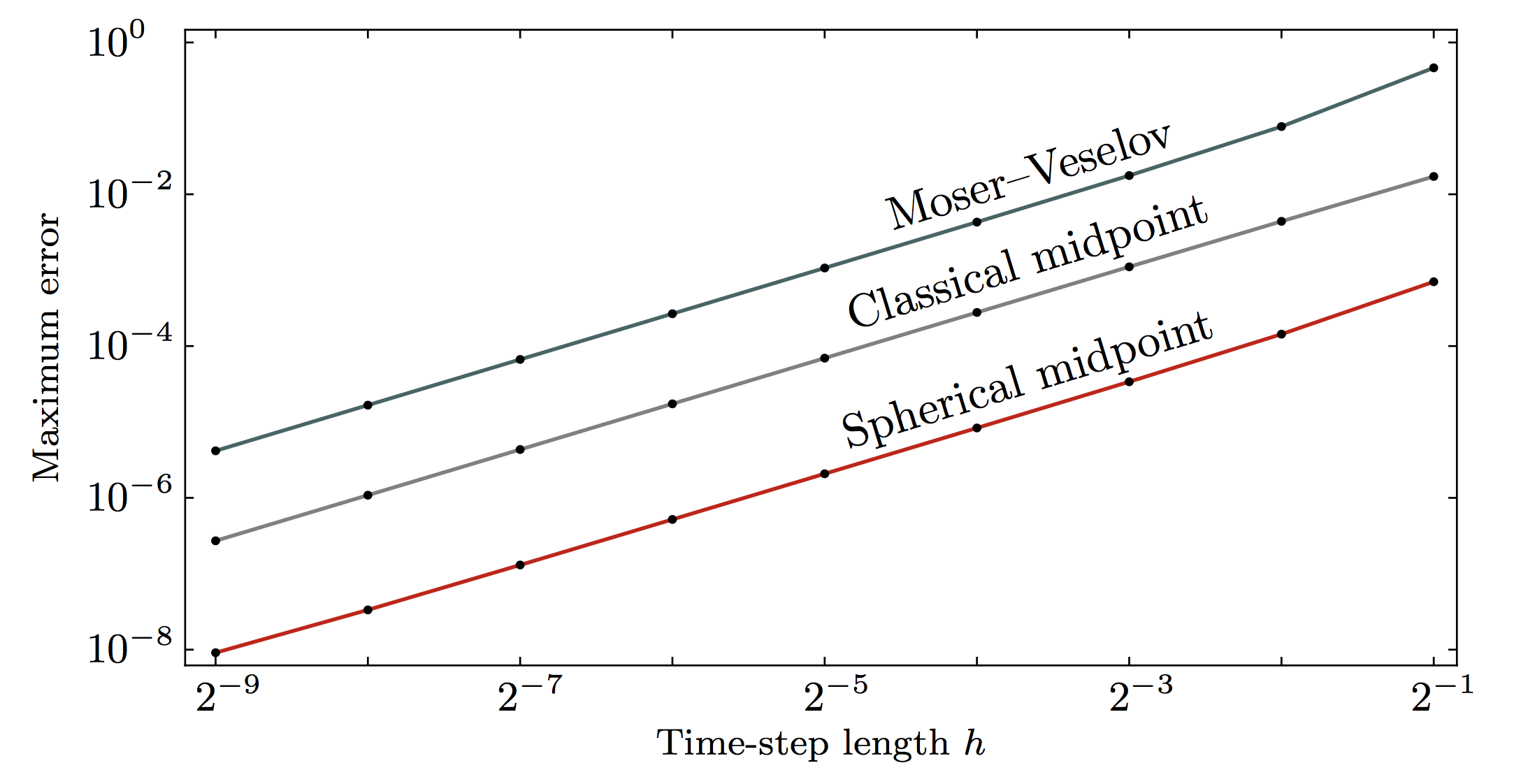
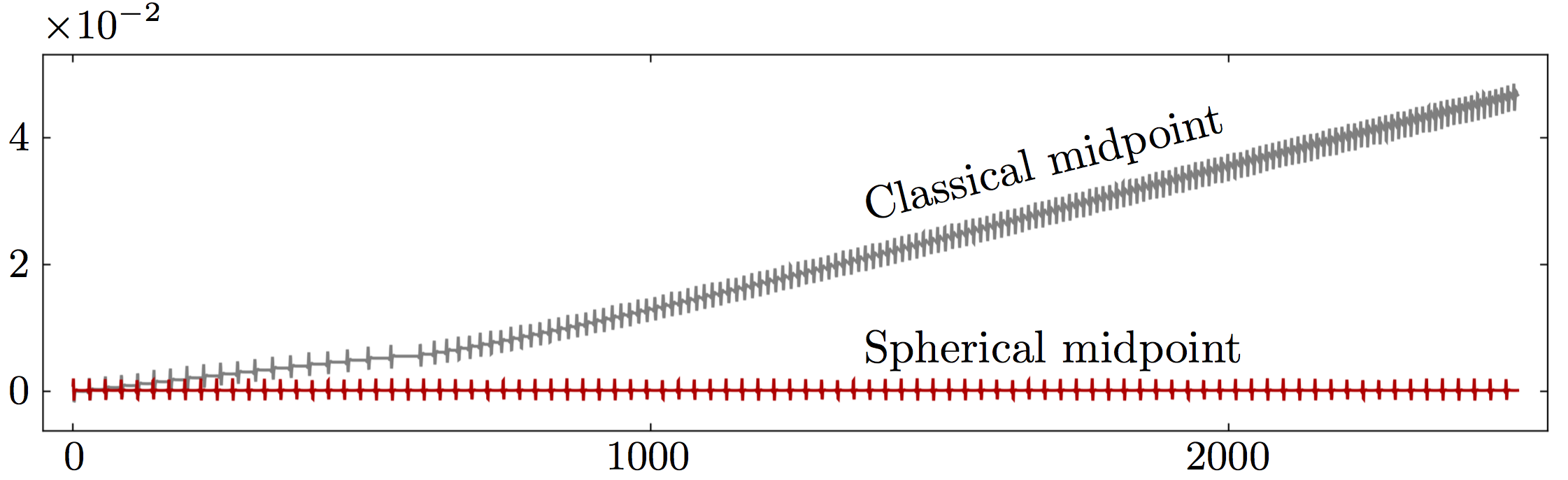
Example 2: irreversible rigid body


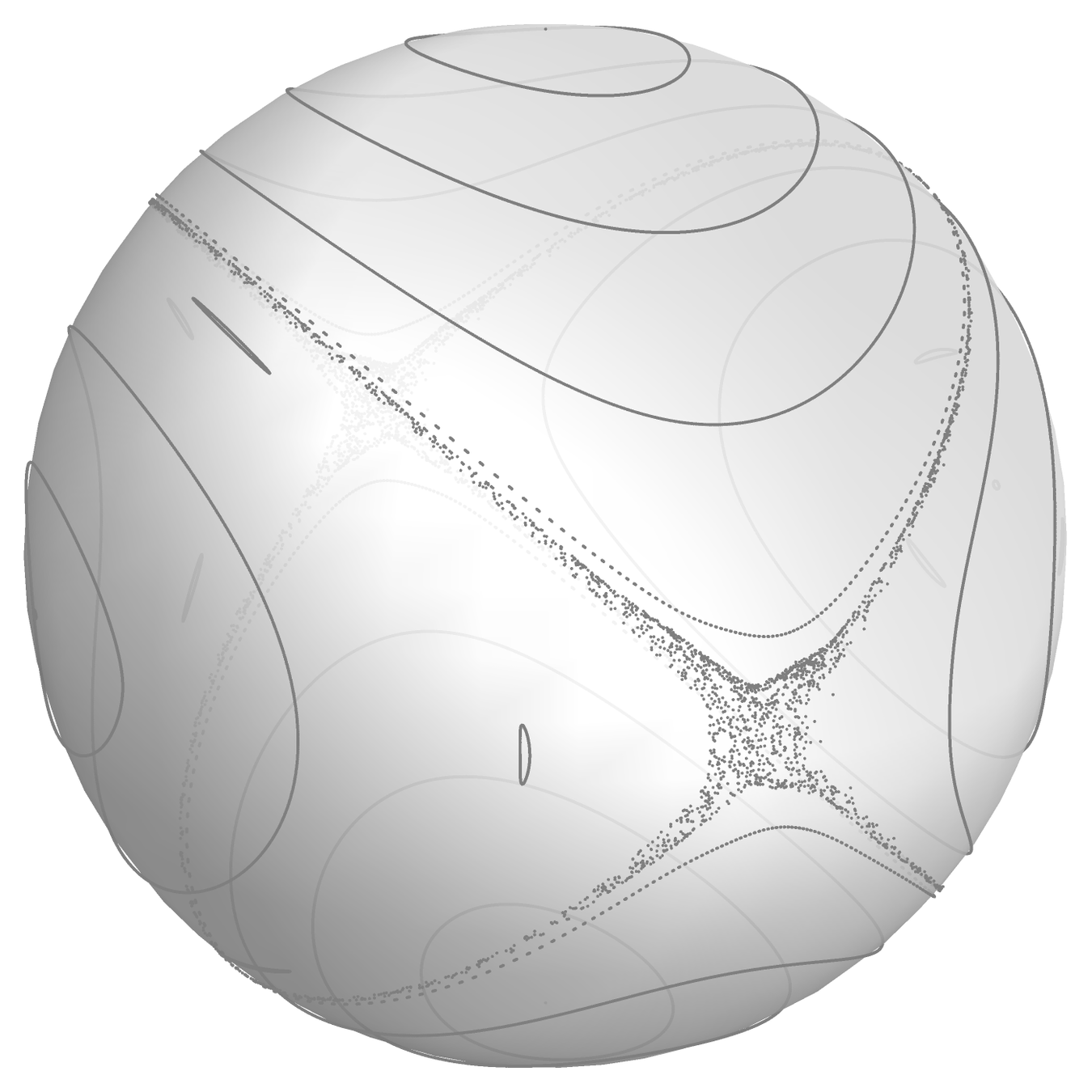
Example 3: development of chaos

Example 4: Landau-Lifshitz PDE
Example 5: atomistic spin dynamics ???

THANKS!
References:
Symplectic integrators for spin systems, Phys. Rev. E, 89:061301, 2014
A minimal-variable symplectic integrator on spheres, Math. Comp., 86, 2325-2344, 2016
Geometry of discrete-time spin systems, J. Nonlin. Sci., 26(5):1507-1523, 2016

*slides at slides.com/kmodin