Long-time simulation of spherical hydrodynamics via quantization
Klas Modin



Collaborator: Milo Viviani

Euler equations of ideal hydrodynamics

Leonhard Euler
Make sense on any Riemannian manifold

Motivation for 2D Euler: geophysical fluid dynamics

Vorticity formulation
Apply curl to \(v\)

level-sets of \(\omega\)
Geometry of 2D Euler
Lie-Poisson system on \(\mathfrak{X}_\mu(S^2)^* \simeq C^\infty_0(S^2) \)

\(G=\mathrm{Diff}_\mu(S^2)\)
\(T_e^*G\simeq\mathfrak g^*\)
Casimir functions:
Finite-dim (weak) co-adjoint orbits:
Statistical mechanics theories for 2D Euler
Idea by Onsager (1949):
- Approximate \(\omega\) by PV for large \(N\)
- Find invariant measure and presume ergodicity
Hamiltonian function:

Statistical mechanics theories for 2D Euler
Idea by Onsager (1949):
- Approximate \(\omega\) by PV for large \(N\)
- Find invariant measure and presume ergodicity
Hamiltonian function:
Onsager's observation:
Pos. and neg. strengths \(\Rightarrow\) energy takes values \(-\infty\) to \(\infty\)

Statistical mechanics theories for 2D Euler
Idea by Onsager (1949):
- Approximate \(\omega\) by PV for large \(N\)
- Find invariant measure and presume ergodicity
Hamiltonian function:
Onsager's observation:
Pos. and neg. strengths \(\Rightarrow\) energy takes values \(-\infty\) to \(\infty\)
\(\Rightarrow\) phase volume function \(v(E)\) has inflection point

Statistical mechanics theories for 2D Euler
Idea by Onsager (1949):
- Approximate \(\omega\) by PV for large \(N\)
- Find invariant measure and presume ergodicity
Hamiltonian function:

Problems with Onsager's theory
- PV solutions far from smooth (\(H^{-1}\) but never \(L^p\))
- \(\Rightarrow\) No Casimir functions
- But experiments and numerical simulations strongly indicate that Casimirs affect long-time behavior

Statistical mechanics theories for smooth solutions
Miller (1990) and Robert & Sommeria (1991): (MRS)
- Maximize entropy of probability distribution of macroscopic states under energy and Casimir constraints
Is the MRS prediction correct?
No!
2D Euler equations are not ergodic
...but perhaps MRS is "generically" correct

Flow ergodic except at "KAM islands"
Poincaré section of finite dimensional Hamiltonian system
A problem for geometric
numerical integration
To test MRS we need to:
- Run long simulations
- Preserve the Casimirs
(energy + enstrophy alone not enough) - Preserve the Lie-Poisson structure
(criterion in MRS)
On \(\mathbb{T}^2\) such discretization exists (sine-bracket)
[Zeitlin 1991, McLachlan 1993]
based on quantization theory by Hoppe (1989)
[Abramov & Majda 2003]
A torus is not a sphere
MRS generally assumed valid also on \(S^2\)
However, non-structure preserving simulations by Dritschel, Qi, & Marston (2015) contradict MRS on \(S^2\)

DQM simulation yield persistent unsteadiness
Our mission: trustworthy discretization on \(S^2\)
2D Euler to isospectral flow via Berezin-Toeplitz quantization
Exists if \(M\) compact quantizable Kähler manifold
Idea: approximate Poisson algebra with matrix algebras
From 2D Euler
To isospectral
Lie-Poisson isospectral flows
Let \(B\colon\mathfrak{g}\to\mathfrak{g}\)
isospectral flow
Analytic function \(f\) yields first integral
Casimir function
Hamiltonian case
Hamiltonian function
Note: Non-canonical Poisson structure (Lie-Poisson)
Explicit B-T quantization on \(S^2\)
[Hoppe, 1989]
- Express \(\omega\) in spherical harmonics expansion \[ \omega = \sum_{l=1}^\infty \sum_{m=-l}^l \omega^{lm}Y_{lm}\]
- Truncate at \(l_{\it max}=N-1\)
- For fixed \(m\), linear map between \((\omega^{lm})_{l=1}^{N-m})\) and \(m\):th diagonal of \(W\)
- Gives \(N\) linear maps
Complicated coefficients, expressed by Wigner 3-j symbols of very high order
Discrete \(S^2\) Laplacian on \(\mathfrak{su}(N)\)
- "Magic" formula [Hoppe & Yau, 1998]
\[\Delta_N W =\frac{N^2-1}{2}\left([X^N,[X^N,W]]- \frac{1}{2}[X_+^N,[X_-^N,W]]- \frac{1}{2}[X_-^N,[X_+^N,W]] \right) \]
banded matrices
Recall
What is \(\Delta_N\) and how compute \(\Delta_N^{-1}W\) ?
(Naive approach requires \(O(N^3)\) operations with large constant)
\(O(N^2)\) operations
- \(\Delta_N\) admits sparse \(LU\)-factorization with \(O(N^2)\) non-zeros
Spatial discretization obtained!
Note: corresponds to
\(N^2\) spherical harmonics
\(O(N^2)\) operations
\(O(N^3)\) operations
Isospectral flow \(\Rightarrow\) discrete Casimirs
Time discretization
Aim: numerical integrator that is
-
isospectral, \(W_{k}\to W_{k+1}\) an isospectral map
necessary to preserve Casimirs
-
symplectic, \(W_{k}\to W_{k+1}\) a Lie-Poisson map \(\mathfrak{su}(N)^*\to\mathfrak{su}(N)^*\)
necessary to (nearly) preserve energy and phase space structure
What about symplectic Runge-Kutta methods (SRK)?
- Not Lie-Poisson preserving!
- Not isospectral!
Isospectral Symplectic
Runge-Kutta methods
[M. & Viviani 2019]
Given \(s\)-stage Butcher tableau \((a_{ij},b_i)\) for SRK
Theorem: method is isospectral and Lie-Poisson preserving on any reductive Lie algebra
Isospectral midpoint method
What now?
Numerical results
Evolution of quantized vorticity with \(N=501\)
Let's run it fast...

Strong numerical evidence against MRS!
Alignment with
point-vortex dynamics
Other initial conditions
What are "generic" initial conditions?
Our interpretation: sample from Gaussian random fields on \(H^{1+\epsilon}(S^2)\)
Non-zero angular momentum
\(N=501\)
Mechanism for long-time behaviour
Observation: large scale motion quasiperiodic
Assumptions for new mechanism:
- Small formations merge to larger (inverse energy cascade)
- Well-separated blobs interact approximately by blob vortex dynamics (BVD)
- Dynamics is not integrable \(\Rightarrow\) blobs continue to merge
- \(k\)-BVD integrable \(\Rightarrow\) quasi-periodicity prevents further mixing
Integrability of PVD and BVD on \(S^2\)
Known since long: \(k\)-PVD integrable for \(k\leq 3\)
What about the 4-blob formations?
4-PVD on \(S^2\) non-integrable in general, but integrable for zero-momentum [Sakajo 2007]
Aref (2007) on PVD:
"a classical mathematics playground"
"many strands of classical mathematical physics come together"
Predictions for Euler on \(S^2\)
For generic initial conditions:
- Momentum small \(\Rightarrow\) 4-PVD is KAM-integrable \(\Rightarrow\) expect 4 non-steady vortex blobs
- Momentum intermediate \(\Rightarrow\) 3-PVD is integrable \(\Rightarrow\) expect 3 non-steady vortex blobs
- Momentum large \(\Rightarrow\) expect 2 large and 1 small vortex blobs
Canonical scale separation
Canonical splitting by stabilizer projection:



initial time
intermediate time
long time
Canonical scale separation
Canonical splitting by stabilizer projection:
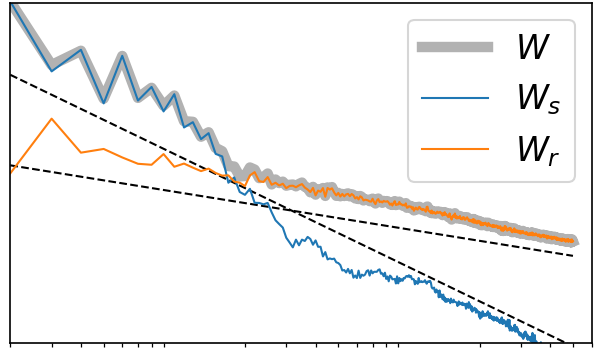
wave number
energy
Thank you!
- M. & Viviani, A Casimir preserving scheme for long-time simulation of spherical ideal hydrodynamics, J. Fluid Mech., 2020
- M. & Viviani, Lie-Poisson methods for isospectral flows, Found. Comp. Math., 2020
- M. & Viviani, Integrability of point-vortex dynamics via symplectic reduction, Arnold Math. J., 2020.
- M. & Viviani. Canonical scale separation in two-dimensional incompressible hydrodynamics, preprint, 2021
- Slides at slides.com/kmodin
- Videos at bitbucket.org/kmodin/euler-sphere-quantization
