Wasserstein-Otto geometry


Klas Modin

Riemannian principal bundles
Invariant Riemannian metric on \(E\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
Invariant Riemannian metric on \(E\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
left co-sets \([g] = g\cdot H \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion


Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion



Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion





Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion





Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion





Riemannian principal bundles
left co-sets \([g] = g\cdot G_{b_0} \)
Semi-invariant Riemannian metric on \(G\)
\(\Rightarrow\) \(\pi\) Riemannian submersion






polar cone
Optimal mass transport (OMT)


Monge problem, \(L^2\) version
Optimal mass transport (OMT)


Monge problem, \(L^2\) version
Riemannian structure of OMT
Riemannian metric
Induced metric
[Benamou & Brenier (2000), Otto (2001)]
Invariance: \(\eta\in\mathrm{Diff}_{\mu_0}(M)\)



Geodesics on \(\operatorname{Diff}(\mathbb{R}^n)\)
Geodesic equation:







Easy to prove:
Polar cone \(K\) is isomorphic to strictly convex smooth functions via \(\phi \mapsto \nabla\phi\)
Hard to prove:
Polar cone \(K\) a section of principal bundle
Geodesics on \(\operatorname{Diff}(\mathbb{R}^n)\)
Geodesic equation:







Easy to prove:
Polar cone \(K\) is isomorphic to strictly convex smooth functions via \(\phi \mapsto \nabla\phi\)
Hard to prove:
Polar cone \(K\) a section of principal bundle
Brenier's decomposition of transport maps
Geodesic distance on \(\operatorname{Diff}(\mathbb{R}^n)\)
Geodesic curve:







In particular:
Monge-Ampere equation on \(\mathbb{R}^n\)
Geodesic curve:







In particular:
Monge-Ampere equation on \(\mathbb{R}^n\)
Geodesic curve:







In particular:
Linear optimal mass transport
Trivial observation: \(\varphi_0(x) = A_0 x\), \(\varphi_1(x) = A_1 x\) linear diffeomorphisms \(\Rightarrow\) geodesic consists of linear diffeomorphisms
Consequence: \(GL(n)\) is totally geodesic subgroup of \(\operatorname{Diff}(\mathbb{R}^n)\)
Corresponding subspace of densities (statistical submanifold): multivariate Gaussians with zero mean
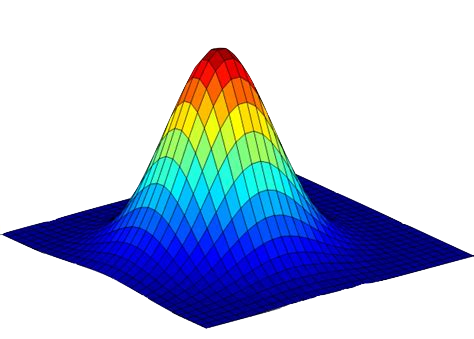
Bundle structure




Bundle structure




Bundle structure




Monge-Ampere equation:
Bundle structure




Factorization theorem:
Bundle structure




Vertical gradient flow:

Bundle structure




Vertical gradient flow:

Bundle structure




Vertical gradient flow:

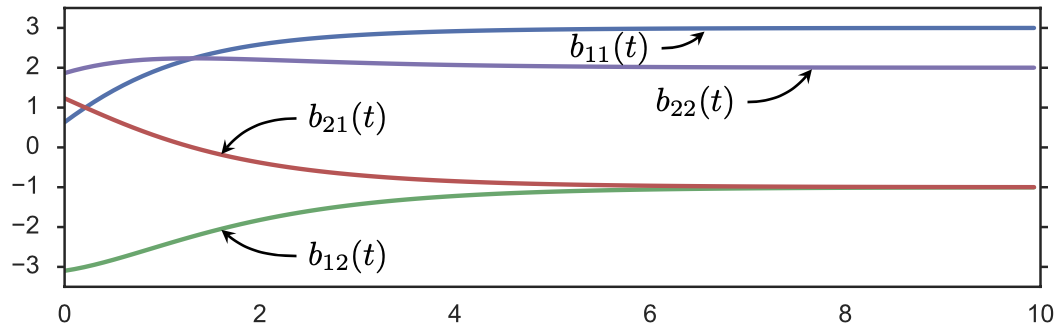
Bundle structure


Horizontal gradient (heat) flow:

Relative entropy
(Kullback-Leibler)
Bundle structure


Horizontal gradient (heat) flow:

Relative entropy
(Kullback-Leibler)
Bundle structure


Horizontal gradient (heat) flow:

Lifted gradient flow on \(K\) for
Bundle structure


Horizontal gradient (heat) flow:

Lifted gradient flow on \(K\) for
Hessian of \(F(P)\) strictly positive on \(K\) \(\Rightarrow\) unique limit!
Bundle structure


Horizontal gradient (heat) flow:

Lifted gradient flow on \(K\) for
Hessian of \(F(P)\) strictly positive on \(K\) \(\Rightarrow\) unique limit!
Bundle structure


Horizontal gradient (heat) flow:

Lifted gradient flow on \(K\) for
Hessian of \(F(P)\) strictly positive on \(K\) \(\Rightarrow\) unique limit!
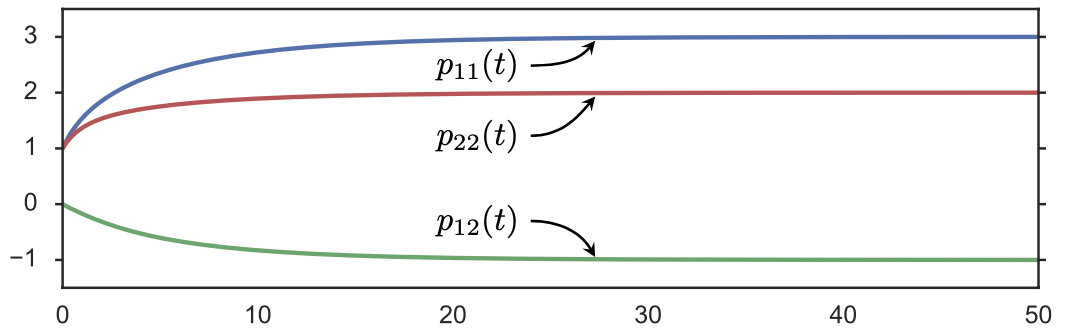
Bundle structure


Horizontal gradient (heat) flow:

Lifted gradient flow on \(K\) for
Hessian of \(F(P)\) strictly positive on \(K\) \(\Rightarrow\) unique limit!
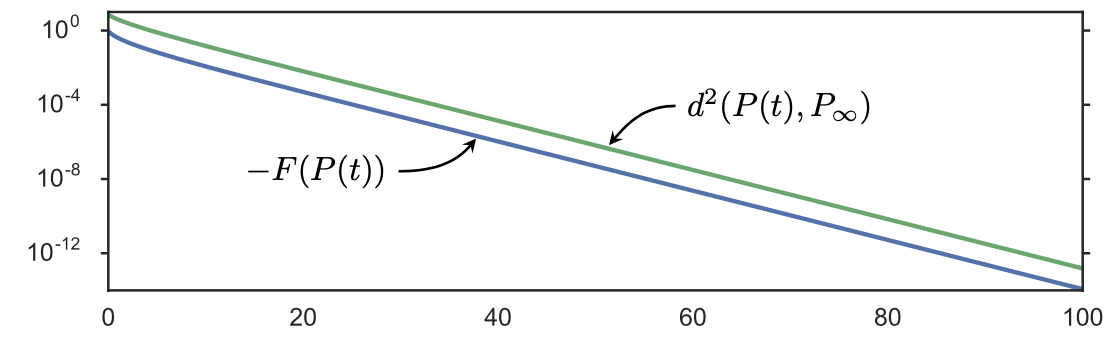
Wasserstein-Otto vs. Fisher-Rao

Wasserstein
Fisher-Rao
Dependent on Riemannian structure of \(M\)
Independent of Riemannian structure of \(M \Rightarrow \mathrm{Diff}(M)\)-invariance
Brockett flow

\(H_N(W)\) relative entropy functional
Functional \(F(Q) = H_N(Q^\top W_1 Q)\) on \(O(n)\)
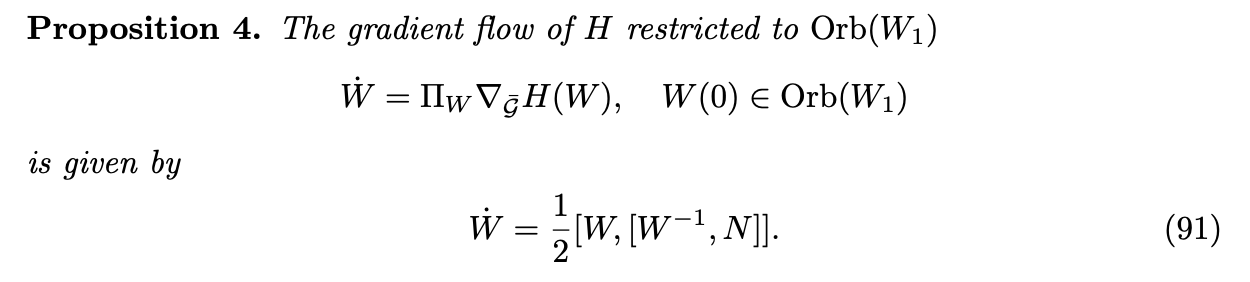
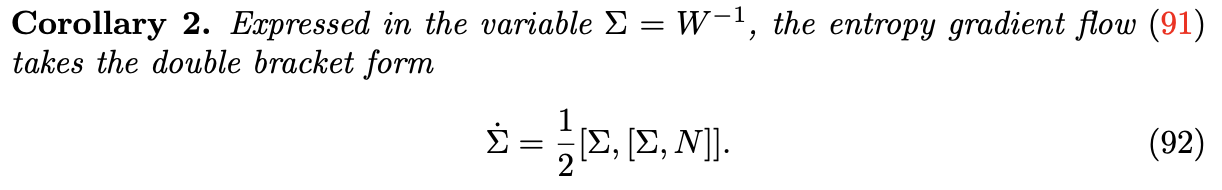

Relative entropy
Heat flow
Wasserstein-Otto metric
\(\Rightarrow\) Riemannian gradient flow \(\dot\rho = -\nabla_{\overline{\mathcal G}}F(\rho)\)
Take \(F(\rho) = \int_M \log(\rho) \rho \Rightarrow \delta F = \log(\rho)+1\)
IPM and Toda
same potential, different Riemannian metrics:
IPM: \(L^2\) on velocity (\(H^{1}\) on stream function)
TODA: \(H^{-1}\) on velocity (\(L^2\) on stream function)
gradients flows on \(\mathrm{Diff}_\mu(S^2)\)
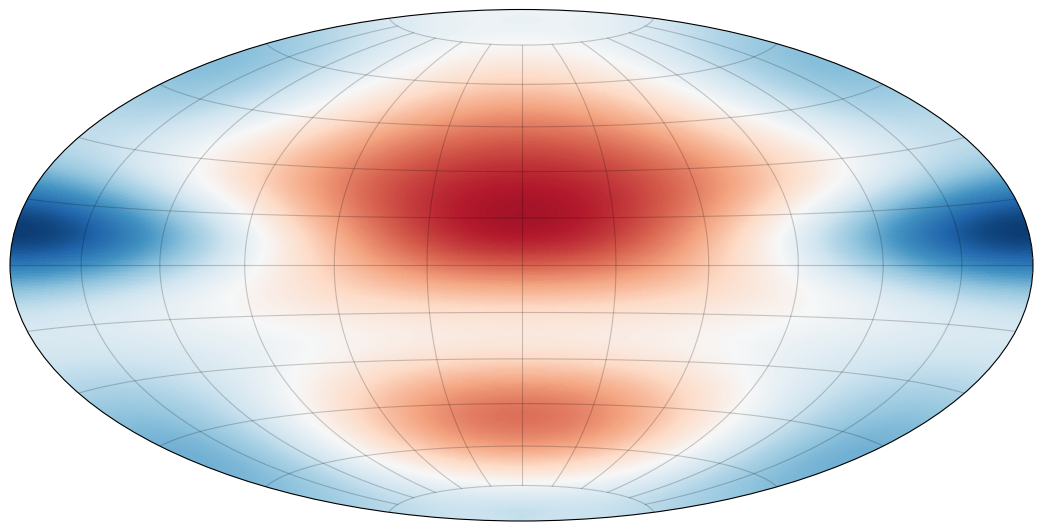
gravity
low density
(light particles)
high density
(heavy particles)


IPM results
Toda results
IPM vs Toda results
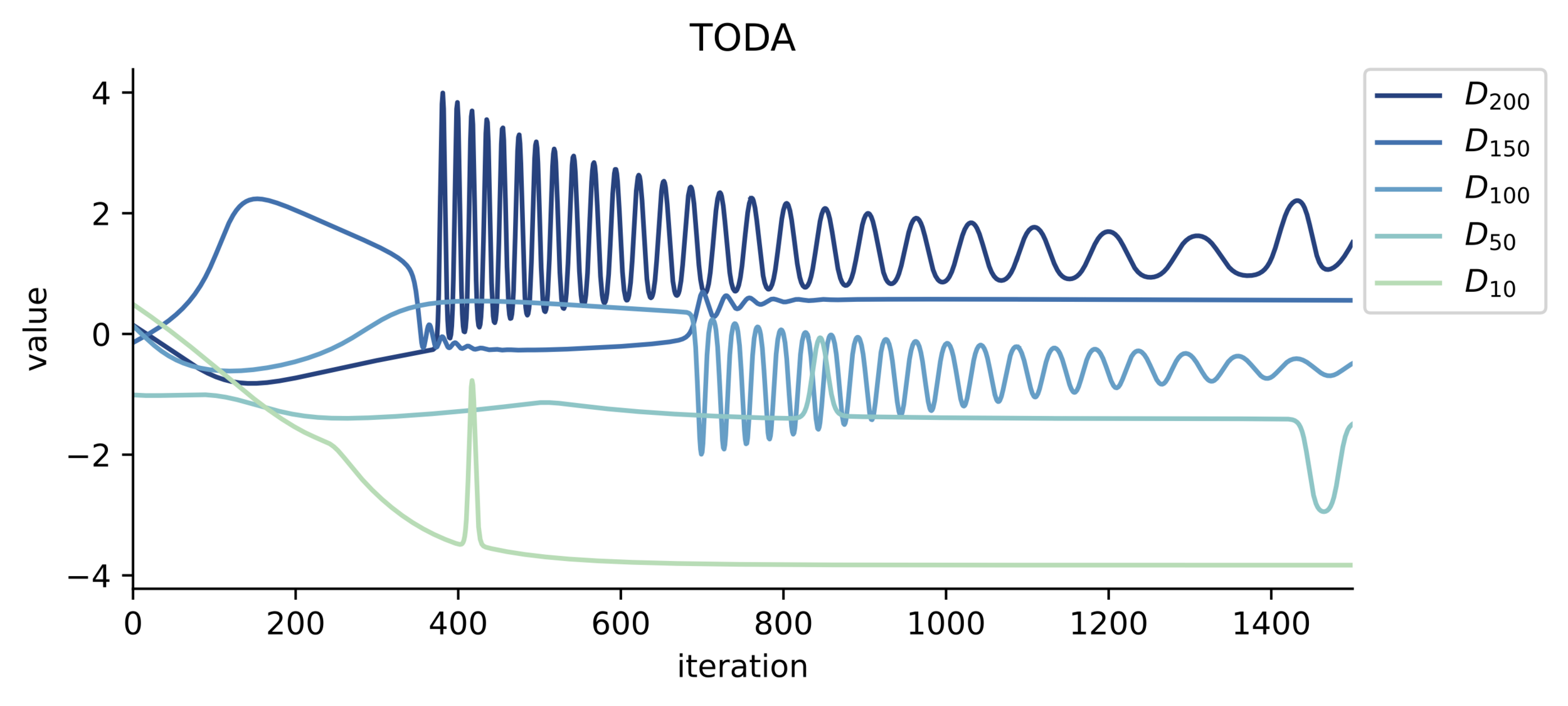
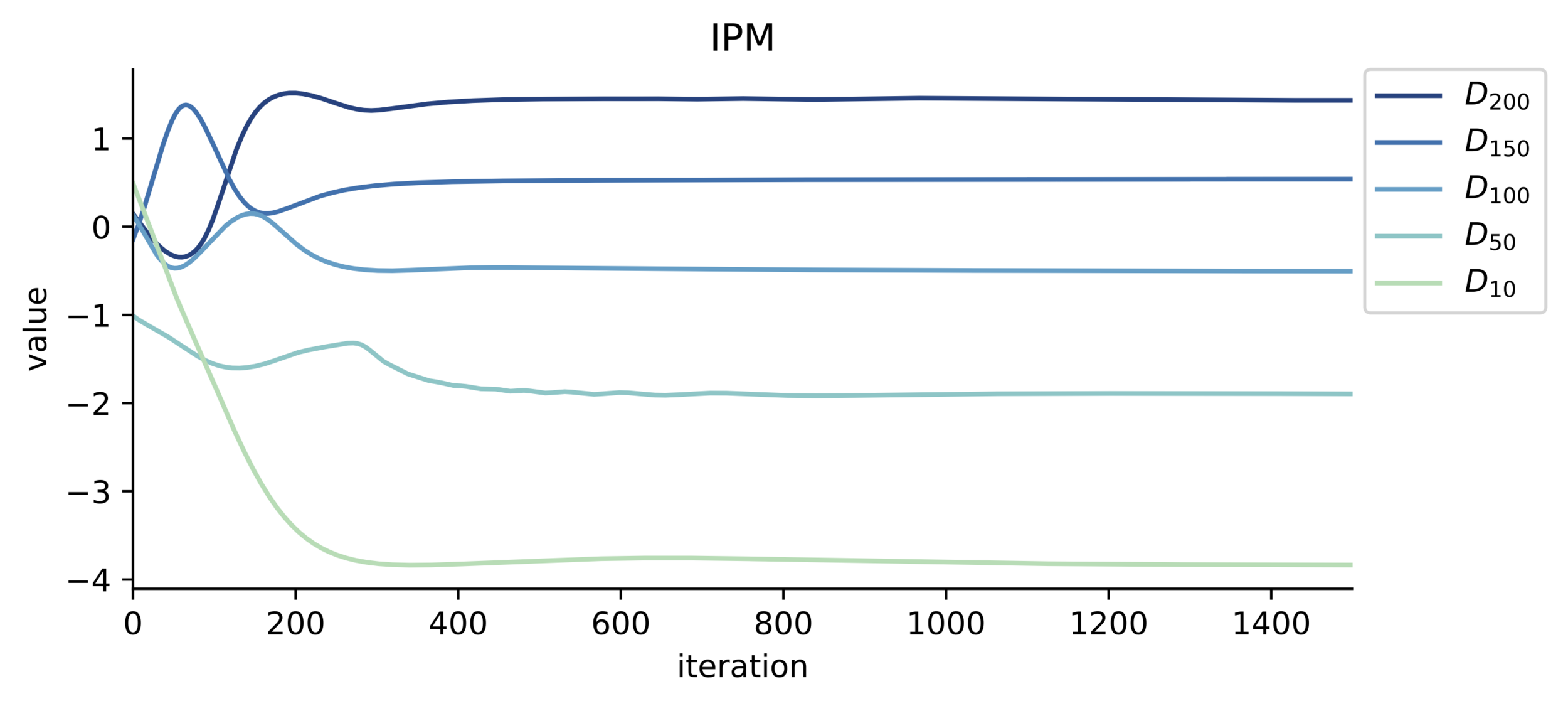
IPM vs Toda results
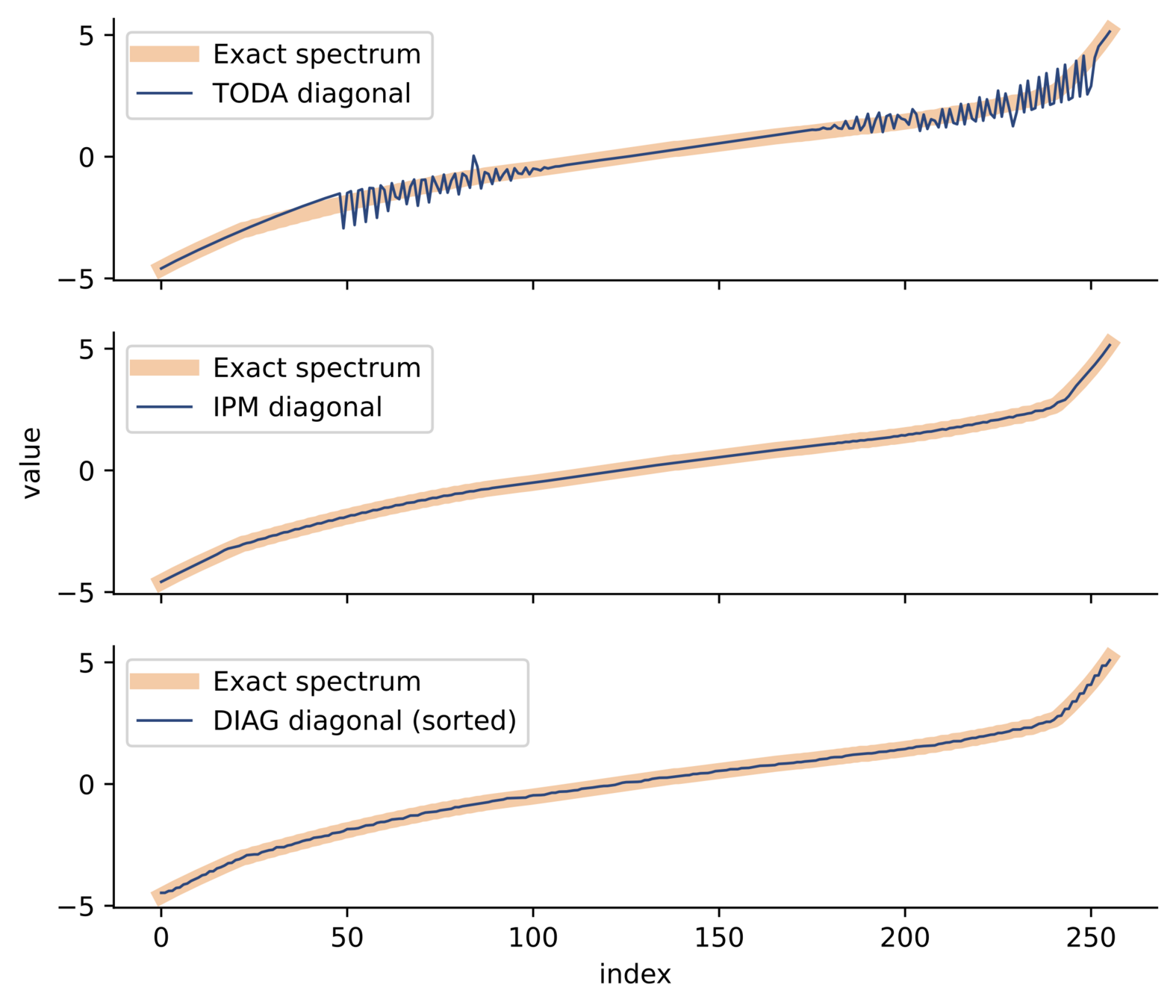
Summary
- IPM and Toda \(\Rightarrow\) Riemannian gradient flows on \(\mathrm{Diff}_\mu(M)\) (or quantized on \(\mathrm{SO}(n)\))
- same potential function
- different (right-invariant) Riemannian metrics
IPM: \(L^2\) Toda: \( H^{-1} \) - Stronger metric \(\Rightarrow\) more regular flow
IPM: ODE on \(\mathrm{Diff}_\mu^s(M)\) (for \(s>2\))
Toda: not ODE on \(\mathrm{Diff}_\mu^s(M)\)