Quantifying the minimum ensemble size

for asymptotic accuracy

of the ensemble Kalman filter

using the degrees of instability

Data Assimilation Seminar

2026/02/02 @RIKEN RCCS, Kobe

* This is joint work with Dr. Miyoshi (Team Principal)

 Nagoya University, Japan

* The author was supported by RIKEN Junior Research Associate Program and JST SPRING JPMJSP2110.

\Psi
\Psi

Kota Takeda

Self-introduction

Kota Takeda

Assistant Prof.

at Nagoya Univ., Japan

https://kotatakeda.github.io/en

Research topics:

Uncertainty Quantification

Fluid mechanics

Data assimilation

Nagoya

Contents

  • Introduction
    • Prediction, m^*, accuracy, Our contributions
  • Background
    • State estimation by EnKF
      • Mathematical formulation, Ensemble Kalman filter, accuracy
    • ​Dynamical instability
      • ​LEs, Unstable subspace literature, Conjecture
  • ​Our approach
  • ​Numerical Result
    • ​Result supporting the conjecture
  • ​Summary

Numerical Weather Prediction

Introduction

Prediction is Hard

(Insert Image: Past Slide p.6 - Typhoon/Chaos)
  • Chaos: Sensitivity to initial conditions makes long-term prediction impossible. -> need ensemble to estimate uncertainty
  • Goal: Estimate the true state from noisy observations to initialize forecasts.

Note: As we all know, weather prediction is difficult due to chaos. We use data assimilation to estimate the current state.

Note: As we all know, weather prediction is difficult due to chaos. We use data assimilation to estimate the current state.

Note: As we all know, weather prediction is difficult due to chaos. We use data assimilation to estimate the current state.

Unpredictable in long-term

Numerical Weather Prediction

State estimation of High dimensional chaotic system

Numerical Weather Prediction

Numerical Weather Prediction

State estimation of High dimensional chaotic system

 Unpredictable in long-term

e.g., Typhoon forecast circles

\sim 10^8

3D grid × variable

Numerical Weather Prediction

Numerical Weather Prediction

State estimation of High dimensional chaotic system

\sim 10^8

3D grid × variable

→ Estimating uncertainty in prediction by ensemble

Fundamental Problem

  • EnKF is standard for high-dimensional geophysical systems .
  • Constraint: Ensemble size ($m$) is limited by computational cost.
    • Real systems: $N_x \sim 10^9$, $m \sim 100$.
  • Risk: Small $m$ leads to Filter Divergence.
  • Question: What is the theoretical minimum $m$ to guarantee "accuracy"?

Orange: Estimate

State estimation by EnKF

Large ensemble

Small ensemble

Success

Failed

(Filter divergence)

Green: True state

Formulation of accuracy: why focus on Noise Scaling?

  • (Standard) Fixed Noise ($r$) Analysis:
    Vary $m^*$ depending on $r$
    Hard to distinguish accuracy similar with the observation noise level.
  • (Our) Asymptotic ($r \to 0$) Analysis:
    • Convergent: Error $\propto r^2$ (Slope 2).
    • Divergent: Error $\approx O(1)$ (Flat).

(Insert Image: Past Slide p.26 - Log-Log Schematic)
Fig: Schematic of Noise-scaled Accuracy

Note: Instead of looking at a fixed noise level, we look at the scaling behavior as noise goes to zero. This gives us a sharp, qualitative distinction between success and failure.

Our Contributions

  1. Reformulation: "Noise-scaled filter accuracy" ($r$-asymptotic accuracy).
  2. The Conjecture: Minimum size is determined by "positive Lyapunov exponents": $$m^* = N_+ + 1$$
  3. Methodology: "Ensemble spin-up and downsizing" strategy.

Note: We propose that $N_+$ is the key number.

Background

Notation: model dynamics

\mathbb{R}^{N_x}
t
\frac{d \boldsymbol{x}}{dt} = \boldsymbol{f}(\boldsymbol{x})
(\boldsymbol{f}: \mathbb{R}^{N_x} \rightarrow \mathbb{R}^{N_x}, \boldsymbol{x}(0) = \boldsymbol{x}_0 \in \mathbb{R}^{N_x})
\boldsymbol{x}(t) = \boldsymbol{\Psi}_t (\boldsymbol{x}_0)

Continuous-time

Evolution map

(\boldsymbol{\Psi}_t : \mathbb{R}^{N_x} \rightarrow \mathbb{R}^{N_x}, t \ge 0)
\boldsymbol{x}_{t_1}
\boldsymbol{x}(t+t_1)
\boldsymbol{\Psi}_t

Discrete-time

\boldsymbol{x}_n = \boldsymbol{\Psi} (\boldsymbol{x}_{n-1})
\boldsymbol{\Psi} = \boldsymbol{\Psi}_\tau \ (\text{for fixed } \tau > 0)

from

\boldsymbol{y}_{1:n} = \{\boldsymbol{y}_i \mid i \le n\}

Filtering problem

\boldsymbol{x}_n

Estimate

n \in \mathbb{N},

known:

\boldsymbol{\Psi},
H,

Obs. up to now

True

Obs.

Estim.

\mathbb{R}^{N_x}
\mathbb{R}^{N_y}
\mathbb{R}^{N_x}
H

...

\boldsymbol{x}_1
\boldsymbol{x}_2
\boldsymbol{x}_0
\boldsymbol{y}_1
\boldsymbol{y}_2
\boldsymbol{\Psi}

...

\overline{\boldsymbol{x}}_1
\overline{\boldsymbol{x}}_2
\overline{\boldsymbol{x}}_0

...

\boldsymbol{\Psi}
\boldsymbol{\Psi}
\boldsymbol{\Psi} = \boldsymbol{\Psi}_t.

Induced from differential equations:

: Model dynamics

\Psi

State space model

\begin{cases} \boldsymbol{x}_n = \boldsymbol{\Psi}(\boldsymbol{x}_{n-1}), \\ \boldsymbol{y}_n = H \boldsymbol{x}_n + \boldsymbol{\xi}_n. \end{cases}
H

: Observation matrix

Assume

H = I.
\boldsymbol{\xi}_n

: Gaussian noise

\sim \mathcal{N}(\boldsymbol{0}, r^2 I).

Filtering Problem

\boldsymbol{\Psi}
\boldsymbol{\Psi}
\boldsymbol{\Psi}
\mathcal{N}(\boldsymbol{0}, r^2 I).

- Estimates by ensemble

- Update:

- Correct mean and covariance 

  using observations

\mathbb{R}^{N_x}
t
y_1
y_2
t_1
t_2
t_3
\tau
t_0

Repeat (I) & (II)...

(II)Analysis

(I) Forecast

\Psi
\boldsymbol{x}_0^{a(1)}
\boldsymbol{x}_0^{a(m)}
\boldsymbol{x}_0^{a(2)}
\boldsymbol{x}_1^{f(1)}
\boldsymbol{x}_1^{a(1)}
\vdots
\boldsymbol{x}_1^{f(m)}
\boldsymbol{x}_1^{a(m)}

Just evolve each sample

Correct samples based on the least squares

X_{n-1}^a \overset{\text{(I)}}{\rightarrow} X_n^f \overset{\text{(II)}}{\rightarrow} X_n^a
\overline{\boldsymbol{x}}_n = \frac{1}{m} \sum_{k=1}^m \boldsymbol{x}_n^{a(k)}

Estimate

X_n^a = (\boldsymbol{x}_n^{a(k)})_{k=1}^m, \\ X_n^f = (\boldsymbol{x}_n^{f(k)})_{k=1}^m

ensemble

ensemble

(Evensen2009)

Ensemble Kalman filter (EnKF)

How to generate estimates?: EnKF

(I) Forecast

\mathrm{rank}(P_n^f) \le m - 1.

Remark:  the rank is restricted as

P_n^f = \operatorname{Cov}_m(\boldsymbol{X}_n^f).

Estimate forecast uncertainty using eigenvalues and vectors of forecast covariance:

(II) Analysis

Stronger correction in higher uncertainty along the direction.

→ rank-deficient

m \le N_x
P_n^f

Why ensemble?

→ No correction in the degenerated direction.

\boldsymbol{x}_1^{f(1)}
\boldsymbol{x}_1^{f(3)}
\boldsymbol{x}_1^{f(2)}
\Psi

Multiplicative inflation

"accutual"

\mathrm{trace}({P_n^f})
P_n^f \rightarrow \alpha^2 P_n^f \ (\alpha \ge 1).

Compensate for underestimated variability of forecasts with a limited ensemble.

(*An efficient implementation is used in practice.)

\mathrm{trace}({\alpha^2 P_n^f})

* The rank of covariance is not improved

\mathrm{rank}({P_n^f}) = \mathrm{rank}({\alpha^2 P_n^f})

Covariance inflation

m

ensemble size

Question: minimum ensemble

Question

How many samples are required

for 'accurate state estimation' using EnKF?

m^*
N.

Disadvantage

-       varies depending on    (out of our scope).
- Hard to distinguish accuracy similar with the observation noise level.

Formulation of accuracy

Question

What is the minimum ensemble size       required

for 'accurate state estimation' using EnKF?

The standard metric for accuracy

obs. noise leve.

m^*
r

for large

\mathrm{mean}_{n \ge N}\mathbb{E}[\mathrm{RMSE}_n] = \mathbb{E}\left[\textstyle{\frac{|\boldsymbol{\delta}_n|}{\sqrt{N_x}}}\right] < r
\limsup_{n\rightarrow \infty}\mathbb{E}[|\delta_n|^2] = O(r^2),

(r-asymptotic) filter accuracy

\boldsymbol{\delta}_n = \boldsymbol{x}_n - \overline{\boldsymbol{x}}_n

: state estimation error.

r^2

: variance of obs. noise,

where

r

squared error

log-log

O(r^2)

Formulation of accuracy

→ Commonly used in mathematical studies.

\mathrm{SE}_n
m^*

Question

What is the minimum ensemble size       required

for 'accurate state estimation' using EnKF?

ensemble

Large

m

Accurate

m

Small

m

ensemble

Inaccurate

Qualitative distinction

← Find minimum 

m = m^*

achieving accuracy!

m^*

Question

What is the minimum ensemble size       required

for 'accurate state estimation' using EnKF?

Advantage:

Qualitative distinction

Summary of EnKF

- Mechanism of EnKF <-> dynamical instability

- Question: minimum ensemble size m*

- (Our) Reformulate accuracy

Dynamical instability

Dynamical instability

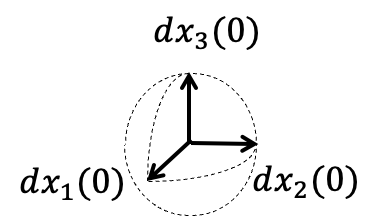
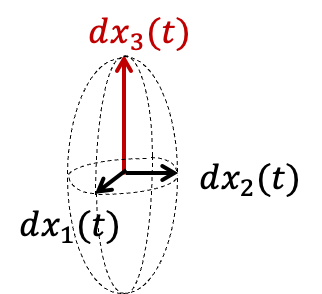
infinitesimal perturbation

D_{\boldsymbol{x}}\boldsymbol{\Psi}_t

expanded

contracted

Jacobian matrix

→ High forecast uncertainty along this direction.

\boldsymbol{x} \mapsto \boldsymbol{\Psi}_t(\boldsymbol{x})
\delta \boldsymbol{x}(t) = D_{\boldsymbol{x}}\boldsymbol{\Psi}_t \delta \boldsymbol{x}(0)

Tangent linear model

linearize

Meaning

     : Asymptotic exponential growth/decay rate

of the i-th principal axis.

positive → growth

negative → decay

Lyapunov exponents

\delta\boldsymbol{x}^{(i)}_t
\delta\boldsymbol{x}^{(i)}_0
\boldsymbol{\Psi}_t
\boldsymbol{\Psi}_t
|\delta\boldsymbol{x}^{(i)}_t| \approx e^{\lambda_i t} |\delta\boldsymbol{x}^{(i)}_0|

Lyapunov exponents:

\lambda_i
\sigma_i(A)

：

A
i
\sigma_i(A)

：

A
i

-singular value of

\lambda_1 \ge \dots \ge \lambda_{N_x}
\lambda_i = \lim_{t \rightarrow \infty} \frac{1}{t} \log \sigma_i(D_{\boldsymbol{x}}\boldsymbol{\Psi}_t)).

Exponents

N_+ := \#\{i \mid \lambda_i > 0\}

Unstable dimension

Low-dimensional unstable subspace

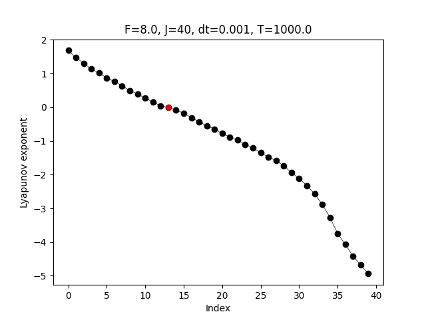
ex.) 40-dim. Lorenz 96 model (chaotic toy model)

\lambda_i
i
0

unstable

stable

  • Navier-Stokes equations

  • Primitive equations

    (core of atmospheric model)

Other dissipative systems too

N_+ = 13 \ll 40 = N_x

Lyapunov exponents

Ansatz (low-dimensional structure):

Most geophysical flows satisfy

N_+ \ll N_x.

Literature: DA

Literature: Math.

(de Wiljes+2018, T.+2024) 

(Sanz-Alonso+2025) 

(González-Tokman+2013) 

m \ge N_x + 1
m \ge 6 N_y
m \ge N_+ + 1

for

using

'Stability' of

\Psi

in unobserved sp.

\Psi

'Lipschitz'

using

too many

additional factor

Accurate initial ensemble aligning with the unstable subspace.

Mathematical analyses have revealed sufficient conditions for      .

m

Literature: Math.

(de Wiljes+2018, T.+2024) 

(Sanz-Alonso+2025) 

(González-Tokman+2013) 

m \ge N_x + 1
m \ge 6 N_y
m \ge N_+ + 1

for

using

'Stability' of

\Psi

in unobserved sp.

\Psi

'Lipschitz'

using

too many

additional factor

Accurate initial ensemble aligning with the unstable subspace.

unrealistic (should be relaxed)

Mathematical analyses have revealed sufficient conditions for      .

m

Focus on

Exploiting Low Dimensionality

Conjecture the minimum ensemble size for filter accuracy with the EnKF is

m^* = N_+ + 1.

(※ with any initial ensemble)

González-Tokman+2013 assume this.

→ How to obtain?

\Psi
\Psi

Tracking only the unstable directions

unstable direction

: critical small ensemble

Exploiting Low Dimensionality

Efficient & Accurate Weather Prediction

Conjecture the minimum ensemble size for filter accuracy with the EnKF is

m^* = N_+ + 1.

(※ with any initial ensemble)

Ansatz

N_+ \ll N_x
m \ll N_x
r

squared error

log-log

O(r^2)

EnKF with

N_{spinup}

: 小

m

: 大

m_0

パラメータ

N_{spinup}

：spin up期間

m_0

：最初のアンサンブル数

m

：削減後のアンサンブル数

n

ねらい：最初は多数のアンサンブルを使うことで真値に近く，不安定方向を向いた「良い」アンサンブルを構成．

Ensemble reduction

                     でアンサンブル数を削減．

SVD/PCAに基づき共分散行列を低ランク近似．

n=N_{spinup}
\mathbb{R}^{N_u}
0

How to obtain?

Algorithm: Downsizing

At step $n = N_{spinup}$:

  1. Take ensemble perturbations $V \in \mathbb{R}^{N_x \times m_0}$.
  2. Compute SVD: $V = U \Sigma W^T$.
  3. Retain leading $m$ singular vectors: $$V_{new} = U[:, 1:m] \Sigma[1:m, 1:m]$$.

Result: Efficient ensemble aligned with instability.

Note: This ensures that when we test $m=14$, for example, those 14 members are the "best possible" 14 members, capturing the most variance.

Require:

Why Spin-up Works? (Alignment)

(Insert Image: Past Slide p.38 - Ensemble Alignment)
  • Natural Alignment: Random perturbations naturally align with the Unstable Subspace (Backward Lyapunov Vectors) over time.
  • Strategy: Spin-up with large $m$, then downsize.
    • Ensures $V^f$ captures the unstable subspace efficiently.

Note: Why do we use spin-up? Because the dynamics naturally rotate the ensemble into the unstable subspace. This gives us an "optimal" initialization for testing the limit.

Summary: Dynamical instability

- Characterize instability via LEs

- key: ensemble alignment connects LEs and m*

- (Our) Proposing method

Numerical Result

Supporting the conjecture

Experimental Setup

  • Model: Lorenz 96 ($N_x = 40$).
  • DA algorithm: ETKF (one of EnKF)
  • Settings:
    • Full observation ($H=I$).
    • Regimes: $F=8$ and $F=16$.
  • Metric: Log-log slope of Squared Error vs. Noise Variance $r^2$.

Numerical Result

To support the conjecture, we perform numerical experiments estimating synthetic data generated by the Lorenz 96 model.

Setup (T.+2025)

obs.:

N_u=40, F=8.0

model：Lorenz96 (                                )

H=I
\eta_n \sim N(0, r^2 I), r > 0

noise: 

EnKF:

m = 12, 13, \dots, 18

(others are chosen appropriately)

dt = 0.01

numerical integration: RungeKutta

obs. interval:

5
N_+ = 13
N_{steps} = 72000

For each     , we compute the dependency of the worst error

on    .

\limsup_{n \rightarrow \infty} \mathbb{E}[|\delta_n|^2]
m
r

Model

To support the conjecture, we perform numerical experiments estimating synthetic data generated by the Lorenz 96 model.

Model

To support the conjecture, we perform numerical experiments estimating synthetic data generated by the Lorenz 96 model.

\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + f
\bm{u} = (u^i)_{i=1}^{N_x} \in \mathbb{R}^{N_x}, f \in \R,

(Lorenz1996, Lorenz+1998)

u^0 = u^{N_x}, u^{-1} = u^{N_x-1}, u^{N_x + 1} = u^1.

Mimics chaotic variation of

physical quantities at equal latitudes.

u

non-linear conserving

linear dissipating

forcing

Lorenz 96 model

(i = 1, \dots, N_x),

Model

To support the conjecture, we perform numerical experiments estimating synthetic data generated by the Lorenz 96 model.

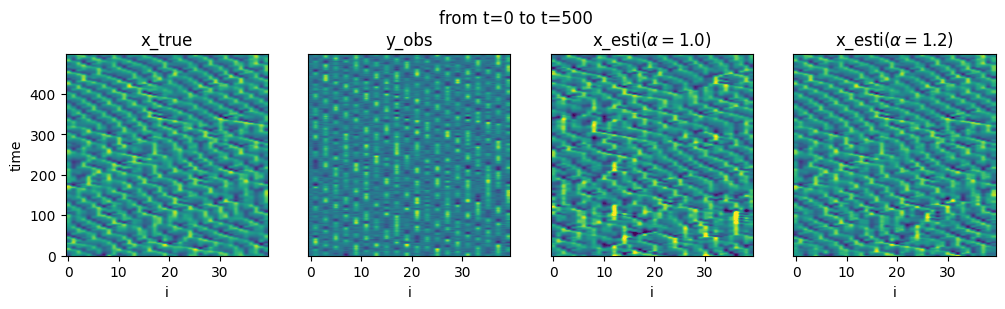
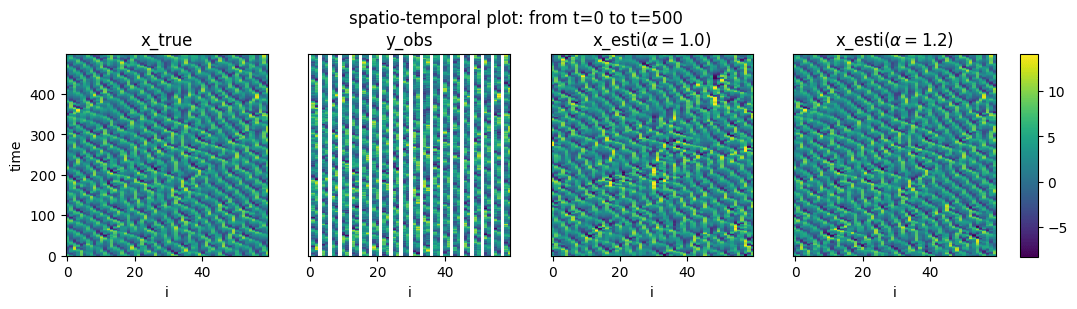
Spatio-temporal plot

u^{i}(t)

Case 1: $F=8$ (Lyapunov Spectrum)

(Insert Image: Past Slide p.37 - Spectrum F=8)
  • Result: 13 Positive Exponents ($N_+ = 13$).
  • Prediction: Minimum size should be $m^ = 14$*.

Note: For F=8, we have 13 positive exponents. Note that N_x is 40, so the instability is low-dimensional.

Case 1: $F=8$ (Accuracy Scaling)

(Insert Image: Past Slide p.47 - Scaling F=8 with highlight)
  • $m \ge 14$ (Red/Gray): Convergent (Slope $\approx 2$).
  • $m < 14$ (Blue): Divergent (Flat).
  • Conclusion: The boundary is exactly at $N_+ + 1$.

Note: Here is the main result. Look at the slope. m=12, 13 are flat (divergent). m=14 and above follow the O(r^2) line. The theory holds.

Case 1: $F=8$ (Ensemble spin-up effect1)

(Insert Image: Fig.3 in manuscript)

$m=14$ (border size)

  • w/ Spin-up: fast Convergent.
  • w/o Spin-up: slow Convergent.
  • Conclusion: Spin up suppress slow-convergence

Case 1: $F=8$ (Ensemble spin-up effect2)

(Insert Image: Fig.4 in manuscript)

$m=14$ (border size), mean-accurate init.

  • w/ Spin-up: fast Convergent.
  • w/o Spin-up: first divergent then slow Convergent.
  • Conclusion: Spin up ensemble alignment

Numerical Result

O(r^2)

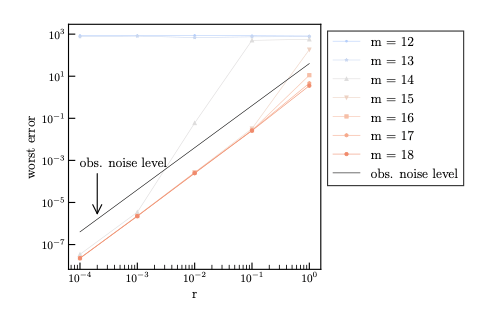
blue

(m <= N_+)

red

(m >= N_+ + 2)

gray

(m = N_+ + 1)

For each     , we compute the dependency of the worst error

on     → log-log plot.

m
r
r
N_+ = 13

Numerical Result

O(r^2)
O(r^2)
r

blue

(m <= N_+)

red

(m >= N_+ + 2)

gray

(m = N_+ + 1)

For each     , we compute the dependency of the worst error

on     → log-log plot.

m
r
N_+ = 13

Numerical Result

O(r^2)
O(r^2)

blue

(m <= N_+)

red

(m >= N_+ + 2)

gray

(m = N_+ + 1)
N_+ + 1

accurate

→ This supports the conjecture.

Inaccurate

r

For each     , we compute the dependency of the worst error

on     → log-log plot.

m
r
N_+ = 13

(filter accuracy)

Case 2: $F=16$ (Higher Instability)

(Insert Image: Paper Fig 5 - Spectrum F=16)
(Insert Image: Paper Fig 6 - Scaling F=16)
  • Spectrum: $N_+ = 15$.
  • Result: Accuracy achieved at $m \ge 16$.
  • Consistency: The rule $m^* = N_+ + 1$ holds for different instability regimes.

Note: We repeated this for F=16. The threshold moved exactly to 16, matching the number of positive exponents plus one.

Summary

New framework: 

$r$-asymptotic filter accuracy

$$ \limsup_{n\rightarrow \infty}\mathbb{E}[\mathrm{SE}_n] = O(r^2)$$

distinguishes convergence/divergence qualitatively.

Main Finding:

The minimum ensemble size is given by

$$m^* = N_+ + 1$$

(numerically verified for Lorenz 96 with).

New supporting method:

The ensemble downsizing for faster alignment of the ensemble with the unstable space.

ensemble

Future work

Future work

Numerical studies: Further experiments validating for high-dimensional & complex systems with multi. zero LEs.

Theoretical analysis: Mechanism of ensemble alignment in the spin-up period.

Extension: Extending this theory to localized methods.

Paper: K.T. and T. Miyoshi (preprint), Quantifying the minimum ensemble size for asymptotic accuracy of the ensemble Kalman filter using the degrees of instability.

Thank you

Code: github.com/KotaTakeda/enkf_ensemble_downsizing

Thank you for your attention

Visit my website!

(T.+2024)

K. T. and T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335,

DOI: 10.1137/24M1637192.

(T.+2025)

K. T. and T. Miyoshi, EGUsphere preprint, https://egusphere.copernicus.org/preprints/2025/egusphere-2025-5144/.

https://kotatakeda.github.io/en/

References

  • (T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
  • (T. 2025) Kota Takeda, Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
  • (Kelly+2014) D. T. B. Kelly, K. J. H. Law, and A. M. Stuart (2014), Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time, Nonlinearity, 27, pp. 2579–260.
  • (Al-Ghattas+2024) O. Al-Ghattas and D. Sanz-Alonso  (2024), Non-asymptotic analysis of ensemble Kalman updates: Effective dimension and localization, Information and Inference: A Journal of the IMA, 13.
  • (Tong+2016a) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability and ergodicity of ensemble based Kalman filters, Nonlinearity, 29, pp. 657–691.
  • (Tong+2016b) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation, Comm. Math. Sci., 14, pp. 1283–1313.
  • (Kwiatkowski+2015) E. Kwiatkowski and J. Mandel (2015), Convergence of the square root ensemble Kalman filter in the large ensemble limit, Siam-Asa J. Uncertain. Quantif., 3, pp. 1–17.
  • (Mandel+2011) J. Mandel, L. Cobb, and J. D. Beezley (2011), On the convergence of the ensemble Kalman filter, Appl.739 Math., 56, pp. 533–541.

References

  •  (de Wiljes+2018) J. de Wiljes, S. Reich, and W. Stannat (2018), Long-Time Stability and Accuracy of the Ensemble Kalman-Bucy Filter for Fully Observed Processes and Small Measurement Noise, Siam J. Appl. Dyn. Syst., 17, pp. 1152–1181.

  • (Evensen2009)Evensen, G. (2009), Data Assimilation: The Ensemble Kalman Filter. Springer, Berlin, Heidelberg.

  • (Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.

  • (Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.

  • (Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.

  • (Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.

  • (Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.

References

  • (Azouani+2014) A. Azouani, E. Olson, and E. S. Titi (2014), Continuous Data Assimilation Using General Interpolant Observables, J. Nonlinear Sci., 24, 277–304.

  • (Sanz-Alonso+2025), D. Sanz-Alonso and N. Waniorek (2025), Long-Time Accuracy of Ensemble Kalman Filters for Chaotic Dynamical Systems and Machine-Learned Dynamical Systems, SIAM J. Appl. Dyn. Syst., pp. 2246–2286.

  • (Biswas+2024), A. Biswas and M. Branicki (2024), A unified framework for the analysis of accuracy and stability of a class of approximate Gaussian filters for the Navier-Stokes Equations, arXiv preprint, https://arxiv.org/abs/2402.14078.

  • (T.2025) K. T. (2025), Error analysis of the projected PO method with additive inflation for the partially observed Lorenz 96 model, arXiv preprint, https://doi.org/10.48550/arXiv.2507.23199.

  • (González-Tokman+2013) C. González-Tokman and B. R. Hunt (2013) Ensemble data assimilation for hyperbolic systems, Physica D: Nonlinear Phenomena, 243(1), pp. 128–142.

  • (T.+2025) K. T. and T. Miyoshi, Quantifying the minimum ensemble size for asymptotic accuracy of the ensemble Kalman filter using the degrees of instability, EGUsphere preprint, https://egusphere.copernicus.org/preprints/2025/egusphere-2025-5144/.

A. Why Squared Error (SE)?

The Problem with RMSE

  • Standard Practice: Time-averaged RMSE at fixed $r$.
  • Limitation: Hard to distinguish "convergence to large error" from "divergence".

Our Solution: Expectation of SE

  • We bound $\mathbb{E}[SE_n] = \mathbb{E}[|x_n - \bar{x}_n^a|^2]$.
  • Jensen's Inequality: $$\mathbb{E}[SE_n] \ge (\mathbb{E}[\text{RMSE}_n])^2$$
  • Implication: Bounding $\mathbb{E}[SE]$ is a stronger condition. If this holds, RMSE is also bounded.

B. Robustness at Large Noise ($r=1.0$)

(Insert Image: Paper Fig B1 - Large Noise Result)
  • Scenario: Large observation noise ($r=1.0$), which violates the small noise assumption.
  • Solution: Shorten the observation interval ($n_{obs}=1, \Delta t=0.001$).
  • Result: Error scales with $r^2$ (or $N_x r^2$).
  • Conclusion: The theory holds even for large noise if observations are frequent enough.

C. Sensitivity to Inflation

(Insert Image: Paper Fig 3 - Inflation Sensitivity)
  • We manually tuned multiplicative inflation $\alpha$.
  • Observation:
    • With Downsizing: Stable for a wide range of $\alpha$.
    • Without Downsizing: Diverges easily or converges very slowly.
  • Future Work: Adaptive inflation (e.g., EnKF-N) would be ideal.

D. Why not Localization?

  • Scope of this study:
    • We focused on the global degrees of instability ($N_+$).
    • Localization modifies the effective dimension.
  • Future Direction:
    • "Local" Lyapunov exponents?
    • "Local" effective ensemble size?
    • Connecting $N_+$ to localization radius is a non-trivial open problem.

E. Ensemble downsizing bias

  • The current implementation of the ensemble downsizing method introduces bias $$mean(X) \neq mean(X_{reduced})$$
  • It still works.
  • An alternative unbiased method is already figured out.

F. Ensemble transform Kalman filter

(Evensen2009)

Require:

ETKF algorithm