Error Analysis of

the Ensemble Square Root Filter for Dissipative Dynamical  Systems

2025/01/23 @Kyoto University

Supervisors

Professor Takashi Sakajo, Kyoto University

Professor Takemasa Miyoshi, Kyoto University & RIKEN

Professor Sebastian Reich, University of Potsdam

Kota Takeda  

*

   Department of mathematics, Kyoto University

*

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

Data Assimilation (DA)

The seamless integration of data and models

Model

Dynamical systems and its numerical simulations

ODE, PDE, SDE,

Numerical analysis, HPC,

Fluid mechanics, Physics

chaos

error

Data

Obtained from experiments or measurements

Statistics, Data analysis,

Radiosonde/Radar/Satellite observation

noise

limited

×

\partial_t \bm{u} + (\bm{u} \cdot \nabla) \bm{u} = - \frac{1}{\rho} \nabla p + \nu \triangle \bm{u} + \bm{f}

Each has uncertainty! (incomplete)

Numerical Weather Prediction (NWP)

Numerical Weather Prediction (NWP) uses atmospheric models

 → Unpredictable in long-term

Typhoon route circles

\partial_t \bm{u} + (\bm{u} \cdot \nabla) \bm{u} = - \frac{1}{\rho} \nabla p + \nu \triangle \bm{u} + \bm{f} \text{ \& } \dots

A small initial error can

grow exponentially fast.

state

time

true/nature state

simulated state

 → Chaotic

NWP and DA

→ chaotic

→ unpredictable in long-term

Numerical Weather Prediction (NWP) uses atmospheric models

Data Assimilation (DA):

simulate

true state

prediction

\widehat{v}_n
v_{n-1}
u_{n-1}

(not accessible directly)

u_n

Atmospheric

model

observation

y_n

Correct using observations (noisy, partial)

Correct      using

v_n

indirect information from the true state

\widehat{v}_n
\partial_t \bm{u} + (\bm{u} \cdot \nabla) \bm{u} = - \frac{1}{\rho} \nabla p + \nu \triangle \bm{u} + \bm{f}

time

t_{n-1}
t_n

NWP & DA

in DA for Numerical Weather Prediction:

chaotic

(x,y,z)\mapsto(x,y)

noisy

partial

observation

true state

\mathbb{R}^3

Example: the trajectory of the Lorenz 63 equation and observations.

Estimating the time series of states of

chaotic dynamical system

using noisy and partial observations.

Three difficulties

Considered

in this talk

Not considered

in this talk

Data Assimilation (DA)

  1. Control
    • ​Nudging/Continuous Data Assimilation
  2. Bayesian Filtering
    • Particle Filter (PF)
    • ​Ensemble Kalman filter (EnKF)
  3. Variational
    • ​​Four-dimensional Variation method (4DVar)

Several formulations & algorithms of DA:

Focus on the main results

(T.+2024) & Thesis

Related to partial observations

cf. Section 5

Not covered

cf. Section 1

Mathematics on DA:

Functional analysis, Probability theory, Dynamical systems,

Partial differential equations, (Numerical analysis)

cf. Section 2, 5

Control formulation

Problem

Keywords/Mathematics

(Olson+2003), (Azouani+2011)

Nudging/Continuous Data Assimilation

Squeezing property, Determining mode/node

AOT-algorithm

\frac{du}{dt} = \mathcal{F}(u),
v = \mathcal{P} u + q, \quad \frac{dq}{dt} = (I - \mathcal{P})\mathcal{F}(v).

If we have noiseless & continuous time observations

through an orthogonal projection

→ copy obs. to the simulated state

(true)

(simulate)

\mathcal{P}: \mathcal{U} \rightarrow \mathcal{Y}.
\text{Estimate the smallest rank of } \mathcal{P} \text{ s.t.}
\lim_{t \rightarrow \infty}|v(t) -u(t)| \rightarrow 0.

PDE (Partial Differential Equations)

Control theory/Synchronization

Incomplete atmospheric data

(Charney+1969)

u = \sum_{|k| \le \lambda} u_k \phi_k + \sum_{|k| >\lambda} u_k \phi_k
v = \sum_{|k| \le \lambda} u_k\phi_k + \sum_{|k| >\lambda} v_k \phi_k
\mathcal{P}_{\lambda} u

copy

converge

(t\rightarrow\infty)
\lambda > 0: \text{ threshold for wavelength}

observed

unobserved

Variational formulation

Problem

Keywords/Mathematics

(Law+2015), (Korn+2009)

Four-dimensional Variational method (4DVar)

Adjoint method to compute gradient

Optimization, Iteration method

\text{Well-posedness of a mininization problem}
v_0 = \argmin_{u_0} J(u_0; \theta)

To estimate the initial state

from observation data

y_1, \cdots, y_N \in \mathcal{Y}
J(u_0;\theta) = \sum_{n=1}^N \|R^{-1/2} (y_n - h(\Psi_{\tau n}(u_0;\theta)))\|^2
u_0 \in \mathcal{U}

minimize a cost function.

\nabla_{u_0} J(u_0)
u_0
y_1
y_2
y_3
y_4
u_1
u_2
u_3
u_4

Supervised Learning

(\theta: \text{ model parameters})
\widehat{\theta} = \argmin_{\theta} J(u_0; \theta)

Back propagation

\text{Suppose } y_n \sim \mathcal{N}(h(u_n), R).

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

State estimation with chaos, noise

Setup: Model

\frac{d u}{dt} = \mathcal{F}(u)
(\mathcal{F}: \mathcal{U} \rightarrow \mathcal{U}, u(0) = u_0 \in \mathcal{U})
u(t) = \Psi_t (u_0)

Model dynamics in

Semi-group in

\mathcal{U}
\mathcal{U}

generates

\mathcal{U}
(\Psi_t : \mathcal{U} \rightarrow \mathcal{U}, t \ge 0)

(assume)

: separable Hilbert space

: separable Hilbert space (state space)

The known model generates

the unknown true trajectory.

t

unknown trajectory

unknown

See Section 3 for other formulations.

Setup: Observation

Discrete-time model (at obs. time)

\mathcal{U}
(\Psi = \Psi_\tau, \tau > 0 \text{: observation interval})

We have noisy observations in

t
y_n = H u_n + \eta_n, \ n \in \mathbb{N}.
(H: \mathcal{L}(\mathcal{U}, \mathcal{Y}), \eta_n \sim N(0, R))

Noisy observation

u_n = \Psi(u_{n-1})

observe

u_1
y_1
u_2
y_2
t_1
t_2
t_3

...

\tau

bounded linear

\in \mathcal{Y}
\mathcal{Y}

(another Hilbert space)

\in \mathcal{Y}
\Psi

at discrete time steps.

(6.4)

(6.2)

Sequential state estimation

\mathcal{U}
t
y_1
y_2
t_1
t_2
t_3

...

\tau

given

\bm{y}_n = \{y_i \mid i \le n\}

Problem

u_n

estimate

\text{For } n \in \mathbb{N},

known:

\Psi,
H,

obs. noise distribution.

y_2
y_3
u_1
u_2
u_3
\Psi
\Psi

Bayesian Data Assimilation

Approach: Bayesian Data Assimilation

\mathbb{P}^{v_n} = \mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

→ construct a random variable       so that

v_n

In other words, compute (approximate)

the conditional distribution                   .

\mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n)

(filtering distribution)

given

\bm{y}_n = \{y_i \mid i \le n\}

Problem

u_n

Estimate

\text{※ } v_n \text{ should be adopted to the filtration } F_n = \sigma(\bm{y}_n).

Sequential Data Assimilation

\mathbb{P}^{v_{n-1}}
y_n
\mathcal{U}
y_n
y_{n+1}
t
t_{n-1}
t_n
t_{n+1}
\tau

For n, two steps with auxiliary variable     .

\hat{v}_n
\Rightarrow \mathbb{P}^{v_n} = \mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

Proposition

\text{Assume } \mathbb{P}^{v_0} = \mathbb{P}^{u_0}.

The n-iterations (I) & (II)

Decomposition into the iterative algorithm

Definition 3.7, 10

(I) Prediction

\Psi

(I) Prediction

\mathbb{P}^{\hat{v}_n}

by model

(II)Analysis

(II) Analysis

\mathbb{P}^{v_n}

by Bayes' rule

\mathbb{P}^{v_n} \propto L_{y_n} \cdot \mathbb{P}^{\hat{v}_n}

likelihood function

Prediction

...

Repeat (I) & (II)

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

State estimation with chaos, noise.

Compute

\mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

Filtering algorithms

Only focus on the Gaussian-based Algorithms

Many filtering algorithms

PF

Ensemble based

EnKF

"Gaussian based"

KF

KF & EnKF

Kalman filter (KF) [Kalman 1960]

  • All Gaussian distribution
  • Closed update of mean and covariance.

Assume: linear F, Gaussian noises

\mathbb{P}^{v_n} = \mathcal{N}(\varpi_n, P_n).
\mathbb{P}^{v_n} \approx \frac{1}{m} \sum_{k=1}^m \delta_{v_n^{(k)}}.

Ensemble Kalman filter (EnKF)

Non-linear extension by Monte Carlo method

  •  
  • Update of ensemble
V_n = [v_n^{(1)},\dots,v_n^{(m)}] \in \mathcal{U}^m

(Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.

(Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.

KF & EnKF

Kalman filter(KF)

Assume: linear F, Gaussian noises

\varpi_n, P_n
\widehat{\varpi}_n, \widehat{P}_n
\varpi_{n-1}, P_{n-1}
y_n

Linear F

Bayes' rule

predict

analysis

Ensemble Kalman filter (EnKF) 

Non-linear extension by Monte Carlo method

V_n
V_{n-1}
\widehat{V}_n
y_n
V_n = [v_n^{(k)}]_{k=1}^m, \widehat{V}_n = [\widehat{v}_n^{(k)}]_{k=1}^m.
\text{nonlinear } \mathcal{F}
\widehat{\varpi}_n, \widehat{P}_n
\varpi_n, P_n

approx.

ensemble

\approx
\approx
\varpi_n \approx \overline{v}_n = \frac{1}{m} \sum_{k=1}^m v^{(k)}_n
P_n = \operatorname{Cov}_m(V_n) = \frac{1}{m-1} \sum_{k=1}^m (v^{(k)}_n - \overline{v}_n) \otimes (v^{(k)}_n - \overline{v}_n)

Two variants

→ next slide

Definition 4.1

  • Two major variants of EnKF:
    • Perturbed Observation (PO): stochastic → sampling error
    • Ensemble Transform Kalman Filter (ETKF): deterministic

Two EnKF variants

\mathcal{U}
t
y_1
y_2
t_1
t_2
t_3

...

\tau
t_0

Repeat (I) & (II)

(II)Analysis

(I) Prediction

\Psi
v_0^{(1)}
v_0^{(m)}
v_0^{(2)}
\widehat{v}_1^{(1)}
v_1^{(1)}
\vdots

(Burgers+1998)

(Bishop+2001)

PO (stochastic EnKF)

\widehat{v}^{(k)}_n = \Psi(v^{(k)}_{n-1}), \quad k = 1, \dots, m.
(I) V_{n-1} \rightarrow \widehat{V}_n: \text{ Evolve each member by model dynamics } \Psi,

(Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.

Stochastic!

Perturbed Observation

\cdot^\top

: A transpose (adjoint) of a matrix (linear operator)

Definition 4.10

y^{(k)}_n = y_n + \eta_n^{(k)}, \quad \eta_n^{(k)} \sim N(0, R), \quad k = 1, \dots, m.
(II) \widehat{V}_n, y_n \rightarrow V_n: \text{Replicate observations,}\\
\text{Then, update each member,}
(\bigstar)
v_n^{(k)} = (I - K_n H) \widehat{v}_n^{(k)} + K_n y_n^{(k)}, \quad k = 1, \dots, m,
\text{where } K_n = \widehat{P}_n H^\top (H \widehat{P}_n H^\top + R)^{-1}, \widehat{P}_n = \operatorname{Cov}_m(\widehat{V}_n).

ETKF (deterministic EnKF)

\widehat{v}^{(k)}_n = \Psi(v^{(k)}_{n-1}), \quad k = 1, \dots, m.
(I) V_{n-1} \rightarrow \widehat{V}_n: \text{ Evolve each member by model dynamics } \Psi,

(Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.

Deterministic!

\text{with the transform matrix } T_n \in \mathbb{R}^{m \times m} \text{ s.t. }
(II) \widehat{V}_n, y_n \rightarrow V_n: \text{Decompose } \widehat{V}_n =\overline{\widehat{v}}_n + d\widehat{V}_n.\\
\overline{v}_n = (I - K_n H)\overline{\widehat{v}}_n + K_n y_n , \quad dV_n = d\widehat{V}_n T_n.
\text{Then, update separately,}
\frac{1}{m-1} d\widehat{V}_n T_n (d\widehat{V}_n T_n)^\top = (I - K_n H) \widehat{P}_n

The explicit representation exists!

(\bigstar)

Ensemble Transform Kalman Filter

Definition 4.13

ETKF (deterministic EnKF)

Ensemble Transform Kalman Filter

\text{The transform matrix } T_n \in \mathbb{R}^{m \times m} \text{ satisfying}
\frac{1}{m-1} d\widehat{V}_n T_n (d\widehat{V}_n T_n)^\top = (I - K_n H) \widehat{P}_n

Lemma (Theorem 4.1)

\text{is uniquely given by}
T_n = \left(I+ \frac{1}{m-1} d\widehat{V}_n^\top H^\top R^{-1} H d\widehat{V}_n \right)^{-\frac{1}{2}}.
\text{(up to unitary transformation)}

ETKF is one of the deterministic EnKF algorithms known as ESRF (Ensemble Square Root Filters).

※ESRF (deterministic EnKF)

ESRF

ETKF

\frac{1}{m-1} d\widehat{V}_n T_n (d\widehat{V}_n T_n)^\top = (I - K_n H) \widehat{P}_n.
T_n \in \mathbb{R}^{m \times m}

EAKF (Ensemble Adjustment Kalman Filter)

\frac{1}{m-1} A_n d\widehat{V}_n (A_n d\widehat{V}_n)^\top = (I - K_n H) \widehat{P}_n.
A_n \in \mathcal{L}(\mathcal{U})

: bounded linear

(Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.

Key perspective of EnKF (KF)

v_n = (I - K_n H) \widehat{v}_n + K_n y_n,
(\bigstar)
\text{where } K_n = \widehat{P}_n H^\top (H \widehat{P}_n H^\top + R)^{-1}.

The analysis state     is the weighted average of

the prediction     and observation

v_n
\widehat{v}_n
y_n

The weight       is determined by estimated uncertainties

K_n
R

: uncertainty in observation (prescribed)

\widehat{P}_n

: uncertainty in prediction (approx. by ensemble)

Inflation (numerical technique)

Issue: Underestimation of covariance       through the DA cycle

→ Overconfident in the prediction → Poor state estimation

(I) Prediction → inflation → (II) Analysis → ...

Rank is improved

Rank is not improved

\widehat{P}_n

Idea: inflating the covariance before (II)

Two basic methods of inflation

\text{Additive } (\alpha \ge 0)
\text{Multiplicative } (\alpha \ge 1)
\text{ETKF}: d\widehat{V}_n \rightarrow \alpha d\widehat{V}_n.
\text{where } d\widehat{V}_n = [\widehat{v}^{(k)}_n - \overline{\widehat{v}}_n]_{k=1}^m, \overline{\widehat{v}}_n = \frac{1}{m} \sum_{k=1}^m \widehat{v}^{(k)}_n.
\text{PO}: \widehat{P}_n \rightarrow \alpha^2\widehat{P}_n,
\text{Only for PO}: \widehat{P}_n \rightarrow \widehat{P}_n + \alpha^2 I_{\mathcal{U}}.

※depending on the implementation

※

Section 4.4

PO

Two EnKF variants

Simple

Stochastic

Require many samples

ETKF

Complicated

Deterministic

Require few samples

Practical !

Inflation: add., multi.

Inflation: only multi.

※depending on the implementation

※

Filtering algorithms

Many filtering algorithms

PF

Ensemble based

EnKF

"Gaussian based"

KF

Deterministic

Stochastic

PO

ETKF

EAKF

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

State estimation with chaos, noise.

Compute

\mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

EnKF: Ensemble & Gaussian approximation.

Error analysis of EnKF

Assumptions on model

(Reasonable)

Assumption on observation

(Strong)

We focus on finite-dimensional state spaces

(\mathcal{U} = \R^{N_u} \text{ for } N_u \in \mathbb{N})

(T.+2024) K. T. & T. Sakajo (2024), SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.

Assumptions for analysis

N_y = N_u, H = I_{N_u}, \eta \sim \mathcal{N}(0, r^2 I_{N_u}), r > 0.

Assumption (obs-1)

"full observation"

Strong!

\exist \rho > 0 \text{ s.t. } \forall u_0 \in B(\rho), \forall t > 0, u(t ; u_0) \in B(\rho).
\exist \beta > 0 \text{ s.t. } \forall u \in B(\rho), \forall v \in \mathbb{R}^{N_u}, \langle F(u) - F(v), u - v \rangle \le \beta | u - v|^2.
\exist \beta > 0 \text{ s.t. } \forall u, v \in B(\rho), |F(u) - F(v)| \le \beta |u - v|.

Assumption (model-1)

Assumption (model-2)

Assumption (model-2')

\forall u_0 \in \R^{N_u}, \frac{du}{dt}(t) = F(u(t)) \text{ has an unique solution, and}

Reasonable

(B(\rho) = \{u \in \R^{N_u} \mid |u| \le \rho \})

"one-sided Lipschitz"

"Lipschitz"

"bounded"

or

Dissipative dynamical system

Dissipative dynamical system

Section 3, 5

Dissipative dynamical systems

Lorenz 63, 96 equations, widely used in geophysics,

\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + f \quad (i = 1, \dots, N_u),

Example (Lorenz 96)

\bm{u} = (u^i)_{i=1}^{N_u} \in \mathbb{R}^{N_u}, f \in \R,

non-linear conserving

linear dissipating

forcing

Assumptions (model-1, 2, 2')

hold

incompressible 2D Navier-Stokes equations (2D-NSE) in infinite-dim. setting

Lorenz 63 eq. can be written in the same form.

→ We can discuss ODE and PDE in a unified framework.

can be generalized

\frac{du}{dt} =
B(u, u)
+
A u
+
f.

bilinear operator

linear operator

dissipative dynamical systems

Mimics chaotic variation of

physical quantities at equal latitudes.

(Lorenz1996) (Lorenz+1998)

u

Dissipative dynamical systems

The orbits of the Lorenz 63 equation.

Literature review

  • Consistency (Mandel+2011, Kwiatkowski+2015)

  • Sampling errors (Al-Ghattas+2024)

  • Stability (Tong+2016a,b)

  • Error analysis (full observation                )

    • PO + add. inflation (Kelly+2014) → next slide

    • ETKF + multi. inflation (T.+2024) → current

    • EAKF + multi. inflation (T.)

  • Error analysis (partial observation) → future  (partially solved, T.)

H = I_{N_u}

How EnKF approximate KF?

How EnKF approximate

the true state?

※ Continuous time formulation (EnKBF)

  • EnKBF with full-obs. (de Wiljes+2018)

Section 6

(m \rightarrow \infty)

Error analysis of PO (prev.)

\text{Let us consider the PO method with additive inflation } \alpha > 0.
\text{Let } e^{(k)}_n = v^{(k)}_n - u_n \text{ for } k = 1, \dots, m.

(Kelly+2014) D. Kelly et al. (2014), Nonlinearity, 27(10), 2579–2603.

\widehat{P}_n \rightarrow \widehat{P}_n + \alpha^2 I_{N_u}

Strong effect! (improve rank)

Theorem (Kelly+2014)

\mathbb{E} [|e^{(k)}_n|^2] \le \theta^n \mathbb{E} [|e^{(k)}_0|^2] + 2m r^2 \frac{1 - \theta^n}{1-\theta}
\text{Then, } \exist \theta = \theta(\beta, \tau, r, \alpha) \in (0, 1), \text{ s.t. }
\text{Let Assumptions (obs-1, model-1,2) hold and }\alpha \gg 1.
\text{for } n \in \mathbb{N}, k = 1, \dots, m.

exponential decay

initial error

\mathbb{E} [\cdot] \text{ : expectation w.r.t. obs. noise and initial uncertainty}

Error analysis of PO (prev.)

\text{Let us consider the PO method with additive inflation } \alpha > 0.
\text{Let } e^{(k)}_n = v^{(k)}_n - u_n \text{ for } k = 1, \dots, m.

variance of observation noise

uniformly in time

(Kelly+2014) D. Kelly et al. (2014), Nonlinearity, 27(10), 2579–2603.

\widehat{P}_n \rightarrow \widehat{P}_n + \alpha^2 I_{N_u}

Strong effect! (improve rank)

Corollary (Kelly+2014)

\limsup_{n \rightarrow \infty} \mathbb{E} [|e^{(k)}_n|^2] \le \frac{2 m}{1-\theta}r^2
\text{Then, } \exist \theta = \theta(\beta, \tau, r, \alpha) \in (0, 1), \text{ s.t. }
\text{Let Assumptions (obs-1, model-1,2) hold and }\alpha \gg 1.
\text{for } k = 1, \dots, m.
\mathbb{E} [\cdot] \text{ : expectation w.r.t. obs. noise and initial uncertainty}

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

State estimation with chaos, noise.

Compute

\mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

EnKF: Ensemble & Gaussian approximation.

PO+add. infl. (Kelly+2014)

Error analysis of ETKF (our)

\text{Let } e_n =\overline{v}_n - u_n \text{ where } \overline{v}_n = \frac{1}{m} \sum_{k=1}^m v^{(k)}_n.
\text{Let us consider the ETKF with multiplicative inflation } \alpha \ge 1.

(T.+2024) K. T. & T. Sakajo (2024), SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.

\mathbb{E}[|e_n|^2] \le \theta^n \mathbb{E}[|e_0|^2] + \frac{N_u r^2(1 - \theta^n)}{1-\theta} + \left(\frac{1 - \Theta}{1 - \theta} - 1\right)D.

Theorem 7.3 (T.+2024)

\text{where } \Theta = \Theta(\beta, \rho, \tau, r, m, \alpha) , D = D(\beta, \rho) > 0.
\text{Then, } \exist \theta = \theta(\beta, \rho, \tau, r, m, \alpha) < 1\text{ s.t.}
\text{Let Assumptions (obs-1, model-1,2') hold.}
\text{Suppose } m > N_u, \operatorname{rank}(P_0) = N_u,\alpha \gg 1, \text{ and}
v_n^{(k)} \in B(\rho) \text{ for } k = 1, \dots, m \text{ and } n \in \N.

※ The same result holds for the EAKF (Theisis)

Error analysis of ETKF (our)

\text{Let us consider the ETKF with multiplicative inflation } \alpha \ge 1.

(T.+2024) K. T. & T. Sakajo (2024), SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.

\limsup_{n \rightarrow \infty} \mathbb{E}[|e_n|^2] \le \frac{N_u r^2}{1-\theta} + \left(\frac{1 - \Theta}{1 - \theta} - 1\right)D.

Corollary 7.3 (T.+2024)

\text{where } \Theta = \Theta(\beta, \rho, \tau, r, m, \alpha) , D = D(\beta, \rho) > 0.
\text{Then, } \exist \theta = \theta(\beta, \rho, \tau, r, m, \alpha) < 1\text{ s.t.}
\text{Let Assumptions (obs-1, model-1,2') hold.}
\text{Suppose } m > N_u, \operatorname{rank}(P_0) = N_u,\alpha \gg 1, \text{ and}
v_n^{(k)} \in B(\rho) \text{ for } k = 1, \dots, m \text{ and } n \in \N.
\text{Let } e_n =\overline{v}_n - u_n \text{ where } \overline{v}_n = \frac{1}{m} \sum_{k=1}^m v^{(k)}_n.

Sketch: Error analysis of ETKF (our)

< e^{-\beta \tau}
= \frac{1}{1 + \alpha^2 r^{-2} \lambda_{min}(\widehat{P}_n)}

①

②

Key point!

\because
(1) \text{ We establish a lower bound of eigenvalues of } \widehat{P}_n \text{ by } \alpha \gg 1.
(2) \text{ If } \widehat{P}_n \text{ is positive-difinite, we have a bound by } \alpha \gg 1.
e^{\beta \tau}

Error growth at (I)

\|(I + \alpha^2 r^{-2} \widehat{P}_n)^{-1}\|_{op}

Error contraction at (II)

norm of error

t

Sketch: Error analysis of ETKF (our)

Strategy: estimate the changes in DA cycle

\widehat{e}_n
(\widehat{e}_n = \overline{\widehat{v}}_n - u_n)
(I)
(II)

expanded

by dynamics

contract &

noise added

e_{n-1}
e_n

Applying Gronwall's lemma to the model dynamics,

(I)
| \widehat{e}_n | \le e^{\beta \tau} |e_{n-1}|

+ {additional term}.

①

\overline{v}_n = (I - K_n H)\overline{\widehat{v}}_n + K_n y_n
e_n = (I - K_n H) \widehat{e}_n + K_n (y_n - H u_n).

subtracting          yields

(II)

From the Kalman update relation

(\bigstar)
u_n

prediction error

② contraction

③ obs. noise effect

estimated by op.-norm

Sketch: Error analysis of ETKF (our)

Key estimates in

Using Woodbury's lemma, we have

I - K_n H = (I + \widehat{P}_n H^\top R^{-1} H)^{-1}.

② contraction

③ obs. noise

(II)
\| \cdot \|_{op}: \text{operator norm}
\|I - K_n H\|_{op} = \|(I + \widehat{P}_n H^\top R^{-1} H)^{-1}\|_{op}

Contraction (see the next slide)

= \|(I + \alpha^2 r^{-2}\widehat{P}_n)^{-1}\|_{op}.
H = I, R = r^2 I

assumption

\|K_n\|_{op} = \|(I + \alpha^2 r^{-2}\widehat{P}_n)^{-1} \alpha^2 r^{-2}\widehat{P}_n\|_{op} \le 1.
(\forall \alpha, r \ge 0, \widehat{P}_n \text{: positive-definite})

Sketch: Error analysis of ETKF (our)

\text{Let } \widehat{\lambda}_n = \lambda_{min}(\widehat{P}_n), \lambda_n = \lambda_{min}(P_n).
(1) \text{ We establish a lower bound of eigenvalues of } \widehat{P}_n \text{ by } \alpha \gg 1.
\widehat{\lambda}_{n-1} \rightarrow \lambda_n \rightarrow \widehat{\lambda}_n
\Rightarrow \widehat{\lambda}_n \ge \frac{e^{-c\tau} \alpha^2 \widehat{\lambda}_{n-1}}{1 + \alpha^2 r^{-2} \widehat{\lambda}_{n-1}}
\therefore \liminf_{n \rightarrow \infty} \widehat{\lambda}_n \ge \frac{r^2 (e^{-c\tau} \alpha^2 - 1)}{\alpha^2} > 0.

estimate the change

\widehat{\lambda}_{n-1} \rightarrow \lambda_n

(inflation & analysis)

\lambda_n = \frac{\alpha^2 \widehat{\lambda}_{n-1}}{1 + \alpha^2 r^{-2} \widehat{\lambda}_{n-1}}
\lambda_n \rightarrow \widehat{\lambda}_n

(prediction)

\widehat{\lambda}_n \ge e^{-c\tau} \lambda_n
\left(c = \frac{8m \beta\rho^2}{m-1}\right)

Comparison

\limsup_{n \rightarrow \infty} \mathbb{E}[|e^{(k)}_n|^2] \le \frac{2 m}{1-\theta}r^2,
\limsup_{n \rightarrow \infty} \mathbb{E}[|e_n|^2] \le \frac{N_u r^2}{1-\theta} + \left(\frac{1 - \Theta}{1 - \theta} - 1\right)D.
\text{Suppose } m > N_u \text{ and } \alpha \gg 1,
\text{Suppose } \alpha \gg 1,

ETKF with multiplicative inflation (our)

PO with additive inflation (prev.)

= O(r^2)
r \rightarrow 0

accurate observation limit

= O(r^2)
O(r^4)
\text{for } k = 1, \dots, m.

Two Gaussian-based filters (EnKF) are assessed in terms of the state estimation error.

due to

due to

Numerical results

Observing System Simulation Experiment (OSSE)

A standard numerical test framework for DA algorithms.

Numerical results

Observing System Simulation Experiment (OSSE)

t
t_1
t_2
t_3
\tau
u_1
u_2
u_3

(1) Compute the true solution       to (6.2).

u_n
\mathcal{U}

Numerical results

Observing System Simulation Experiment (OSSE)

t
t_1
t_2
t_3
\tau
u_1
u_2
u_3

(2) Generate random observations       as in (6.4).

y_n

(1) Compute the true solution       to (6.2).

u_n
\mathcal{U}
y_1
y_2
y_3

Numerical results

Observing System Simulation Experiment (OSSE)

t
t_1
t_2
t_3
\tau
v_n

(3) Assimilate the observed data      and obtain the analysis states       using a data assimilation algorithm.

y_n

(2) Generate random observations       as in (6.4).

y_n

(1) Compute the true solution       to (6.2).

u_n
\mathcal{U}
v_1
v_2
v_3
y_1
y_2
y_3

DA algorithm

Numerical results

Observing System Simulation Experiment (OSSE)

t
t_1
t_2
t_3
\tau

(2) Generate random observations       as in (6.4).

y_n

(1) Compute the true solution       to (6.2).

u_n
\mathcal{U}
v_1
v_2
v_3

(3) Assimilate the observed data      and obtain the analysis states       using a data assimilation algorithm.

y_n
v_n

(4) Compute the error between       and       for n = 1, 2, ...

u_n
v_n
e_1
e_2
e_3
u_1
u_2
u_3

Numerical results

OSSE: ETKF for the Lorenz 96 equation

N_u = 40, m = N_u+1 = 41, r = 1.0.
SE = \mathbb{E}[|e_n|^2]
n
\le N_u r^2 + ...

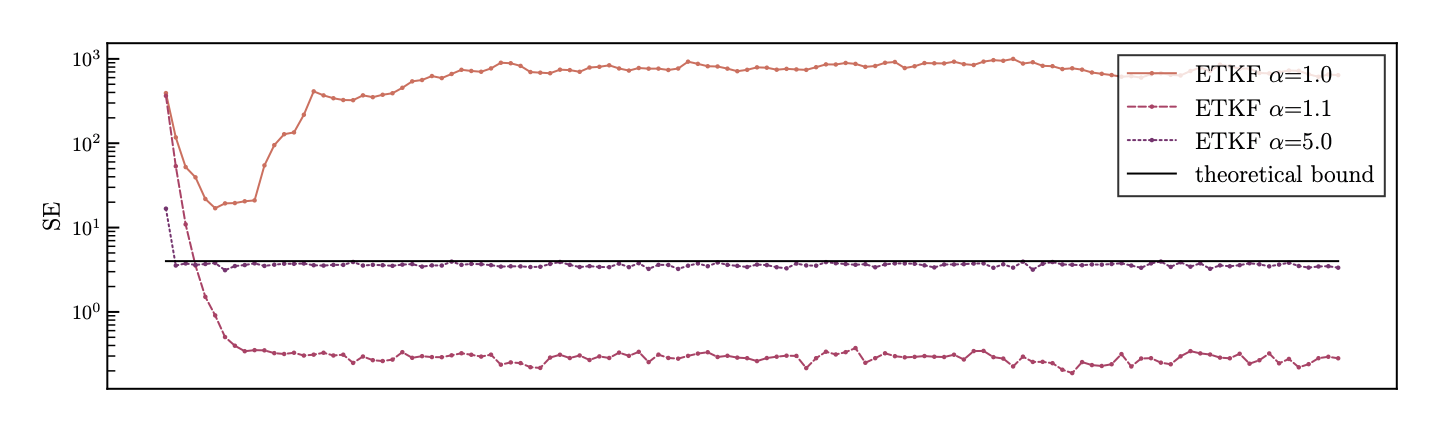
From Theorem 7.3

→ theoretical bound

(\text{Suppose } \theta \ll 1)

strong inflation

weak inflation

no inflation

Numerical results

O(r^2)

Dependency on observation noise variance     .

r^2

Numerical results

Animation

Introduction

Setup

​ Bayesian filtering

 Algorithms

Results (Error analysis)

​ Existing results for EnKF

 My results

Summary & Discussion

Contents

Related sections in Thesis

 Section 1, 2, 5

 

 Section 3

 Section 4

 

 Section 6

 Section 7

Section 8

State estimation with chaos, noise.

Compute

\mathbb{P}^{u_n}({}\cdot{} | \bm{y}_n).

EnKF: Ensemble & Gaussian approximation.

PO+add. infl. (Kelly+2014)

ESRF+multi. infl. (T.+2024)

Summary

We focus on

The sequential state estimation using model and data.

Results

Error analysis of a practical DA algorithm (ETKF)

under an ideal setting (T.+2024).

Discussion

Two issues with extending our analysis.

→ should be relaxed in the future

(rank deficient, non-symmetric)

Discussion

Current

(T.+2024)

1. Partial observation

2. Small ensemble

m \le N_u
N_y < N_u, H \in \mathbb{R}^{N_y \times N_u}

3. Infinite-dimension

\text{state space } \mathcal{U}: \text{Hilbert space},
\text{observation space } \mathcal{Y} \subset \mathcal{U}.

partially solved (T.)

extend

Future

→ Issue 1, 2

→ Issue 1

→ Issue 1

Issues:

  1. rank deficient
  2. non-symmetric

Discussion

\|(I + \widehat{P}_n H^\top R^{-1} H)^{-1}\|_{op} \ge 1.
\text{If } m \le N_u \text{ or } N_y < N_u, H \in \mathbb{R}^{N_y \times N_u}, R \in \mathbb{R}^{N_y \times N_y},

Issue 1 (rank deficient)

\text{then,}

② Error contraction in (II)

1. Partial observation

2. Small ensemble

Discussion

\|(I + \widehat{P}_n H^\top R^{-1} H)^{-1} \widehat{P}_n H^\top R^{-1} H\|_{op} \le 1.
\text{Let } N_y < N_u, H \in \mathbb{R}^{N_y \times N_u}, R \in \mathbb{R}^{N_y \times N_y}.

Issue 2 (non-symmetric)

\text{If } \widehat{P}_n H^\top R^{-1} H \text{ is symmetric then,}

③ bound of obs. noise

If non-symmetric, it doesn't hold in general.

Example

A = \left[ \begin{array}{cc} a & 0 \\ b & 0 \end{array} \right] \Rightarrow \|(I + A)^{-1} A\|_{op} = \frac{\sqrt{a^2 + b^2}}{1+a} > 1.
(a > 0, b^2 \ge 1 + 2a)

Discussion

Infinite-dimension

Theorem (Kelly+2014) for PO + add. infl.

Theorem (T.+2024) for ETKF + multi. infl.

\text{state space } \mathcal{U}: \text{Hilbert space},
\text{observation space } \mathcal{Y} \subset \mathcal{U} \text{: Hilbert space}.

doesn't hold

(due to Issue 1: rank deficient)

※with full-observations

(ex: 2D-NSE with the Sobolev space)

(     improve rank)

\because

still holds

Summary

I focus on

Sequential state estimation using model and data.

Results

Error analysis of a practical DA algorithm (ETKF)

under an ideal setting (T.+2024).

Discussion

Two issues with extending our analysis.

→ should be relaxed

(rank deficient, non-symmetric)

→ other problems in the future

Future Plans

NWP /

Fluid Mechanics

Thesis

DA

UQ

UQ (Uncertainty Quantification):

The quantitative studies of uncertainties in the real world applications.

Mathematics:

Functional analysis

Gronwall's inequality

Future Plans

NWP /

Fluid Mechanics

Thesis

DA

UQ

Collaborating with

Numerics, Machine Learning

Contributing to NWP

Continuing

Developing

novel algorithms

Other applications

Mathematics:

Functional analysis

Gronwall's inequality

Numerical analysis

Lyapunov analyis

Large deviations

Operator algebra

Computational topology

...

UQ (Uncertainty Quantification):

The quantitative studies of uncertainties in the real world applications.

Data Assimilation (DA)

  1. Control
    • ​Nudging/Continuous Data Assimilation
  2. Bayesian
    • Particle Filter (PF)
    • ​Ensemble Kalman filter (EnKF)
  3. Variational
    • ​​Four-dimensional Variation method (4DVar)

PDE

Machine

Learning

Back Prop.

Supervised Learning

Optimization

Dynamical system

SDE

Dynamics

Uncertainty Quantification

Probability/Statistics

& related topic

Random ODE

Numerical Analysis

structure-preserving

Numerical error

Lyapunov

analysis

Operator Algebra

Koopman operator

Quantum DA

Optimal Transport

Diffusion AI

Future plan

References

  • (T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
  • (T.) Kota Takeda, Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
  • (Kelly+2014) D. T. B. Kelly, K. J. H. Law, and A. M. Stuart (2014), Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time, Nonlinearity, 27, pp. 2579–260.
  • (Al-Ghattas+2024) O. Al-Ghattas and D. Sanz-Alonso  (2024), Non-asymptotic analysis of ensemble Kalman updates: Effective dimension and localization, Information and Inference: A Journal of the IMA, 13.
  • (Tong+2016a) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability and ergodicity of ensemble based Kalman filters, Nonlinearity, 29, pp. 657–691.
  • (Tong+2016b) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation, Comm. Math. Sci., 14, pp. 1283–1313.
  • (Kwiatkowski+2015) E. Kwiatkowski and J. Mandel (2015), Convergence of the square root ensemble Kalman filter in the large ensemble limit, Siam-Asa J. Uncertain. Quantif., 3, pp. 1–17.
  • (Mandel+2011) J. Mandel, L. Cobb, and J. D. Beezley (2011), On the convergence of the ensemble Kalman filter, Appl.739 Math., 56, pp. 533–541.

References

  •  (de Wiljes+2018) J. de Wiljes, S. Reich, and W. Stannat (2018), Long-Time Stability and Accuracy of the Ensemble Kalman-Bucy Filter for Fully Observed Processes and Small Measurement Noise, Siam J. Appl. Dyn. Syst., 17, pp. 1152–1181.

  • (Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.

  • (Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.

  • (Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.

  • (Dieci+1999) L. Dieci and T. Eirola (1999), On smooth decompositions of matrices, Siam J. Matrix Anal. Appl., 20, pp. 800–819.

  • (Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.

  • (Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.

Appendix

Further result for partial obs.

The projected PO + add. infl. with partial obs. for Lorenz 96

\text{Let } N_u = 3N \text{ for } N \in \mathbb{N}, H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top \in \mathbb{R}^{N_y \times N_u},
\text{where } (\phi_i)_{i=1}^{N_u} \text{ is a standard basis of } \mathbb{R}^{N_u}.

Illustration (partial observations for Lorenz 96 equation)

○

○

×

○

○

×

○

○

×

○

○

×

○: observed

×: unobserved

u^1
u^2
u^3
u \in \mathbb{R}^{3N}
N_u = 3N, N_y = 2N

the special partial obs. for Lorenz 96

Further result for partial obs.

The projected PO + add. infl. with partial obs. for Lorenz 96

Theorem (T.)

\limsup_{j \rightarrow \infty} \mathbb{E}[\| e^{(k)}_j \|^2] \le \frac{4 \min\{m, N_u\}}{1-\theta}r^2
\text{For } h \ll 1 \text{ and } \alpha \gg 1, \exist \theta = \theta(\beta, h, r, \alpha) \in (0, 1), \text{ s.t. }
\text{for } k = 1, \dots, m.
\text{Let } N_u = 3N \text{ for } N \in \mathbb{N}, H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top \in \mathbb{R}^{N_y \times N_u},
\text{where } (\phi_i)_{i=1}^{N_u} \text{ is a standard basis of } \mathbb{R}^{N_u}, \text{ and let } \|\cdot\| = \sqrt{|\cdot|^2 + |H\cdot|^2}.
\text{Let } v_j^{(k)} \in B(\rho) \text{ for } k = 1, \dots, m, \text{ and } j \in \N.

The projected add. infl.:

\widehat{C}_j \rightarrow H^\top H(\widehat{C}_j + \alpha^2 I_{N_u})H^\top H

key 2

key 1

Problems on numerical analysis

  1. Discretization/Model errors
  2. Dimension-reduction for dissipative dynamics
  3. Numerics for Uncertainty Quantification (UQ)
  4. Imbalance problems

1. Discretization/Model errors

Motivation

- Including discretization errors in the error analysis.

- Consider more general model errors and ML models.

- Error analysis with ML/surrogate models.

cf.: S. Reich & C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press.

 

Question

- Can we introduce the errors as random noises in models?

- Can minor modifications to the existing error analysis work?

\widetilde{\Psi}_t(x) = \Psi_t(x) + \eta_t ?

2. Dimension-reduction for dissipative dynamics

Motivation

- Defining "essential dimension"                      and relaxing the condition:

-          should be independent of discretization.

cf.: C. González-Tokman & B. R. Hunt (2013), Ensemble data assimilation for hyperbolic systems, Physica D: Nonlinear Phenomena, 243(1), 128-142.

N_{ess} \le N_x
m > N_x \rightarrow m > N_{ess}
N_{ess}

Question

- Dissipativeness, dimension of the attractor？

- Does the dimension depend on time and state? (hetero chaos)

- Related to the SVD and the low-rank approximation?

Attractor

3. Numerics for UQ

Motivation

- Evaluating physical parameters in theory.

- Computing the Lyapunov spectrum of atmospheric models.

- Estimating unstable modes (e.g., singular vectors of Jacobian).

cf.: T. J. Bridges & S. Reich (2001), Computing Lyapunov exponents on a Stiefel manifold. Physica D, 156, 219–238.

F. Ginelli et al. (2007), Characterizing Dynamics with Covariant Lyapunov Vectors, Phys. Rev. Lett. 99(13), 130601.

Y. Saiki & M. U. Kobayashi (2010), Numerical identification of nonhyperbolicity of the Lorenz system through Lyapunov vectors, JSIAM Letters, 2, 107-110.

Question

- Can we approximate them only using ensemble simulations?

- Can we estimate their approximation errors?

4. Imbalance problems

Motivation

- Assimilating observations can break the balance relations inherited from dynamics. → numerical divergence

(e.g., the geostrophic balance and gravity waves）

- Explaining the mechanism (sparsity or noise of observations?).

- Only ad hoc remedies (Initialization, IAU).

cf.: E. Kalney (2003), Atmospheric modeling, data assimilation and predictability, Cambridge University Press.

Hastermann et al. (2021), Balanced data assimilation for highly oscillatory mechanical systems, Communications in Applied Mathematics and Computational Science, 16(1), 119–154.

Question

- Need to define a space of balanced states?

- Need to discuss the analysis state belonging to the space?

- Can we utilize structure-preserving schemes?

balanced states