Michael Küffmeier (Carlsberg reintegration fellow)

On the role of infall on planet-forming disks

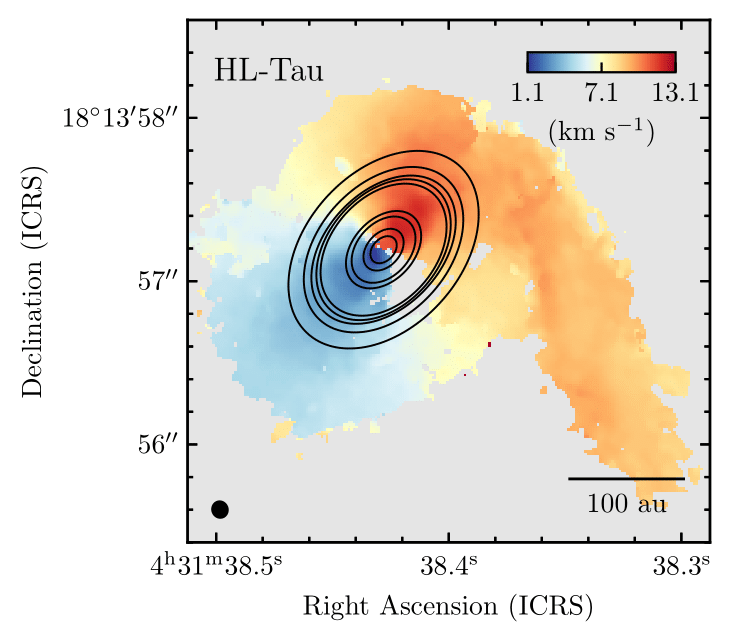
SU Aur

SU Aur

synthetic image

C. Granzow Holm, T. Haugbølle (NBI), J. Pineda (MPE), D. Segura-Cox (Rochester), S. Reißl, C. P. Dullemond (ITA)

Ginski et al. 2021

Krieger et al. 2021

History of modeling disk formation

spherical core collapse:

rotation

magnetization (mass-to-flux ratio)

non-ideal MHD effects

dust evolution

turbulence

useful for parameter studies

\rho(r) = \frac{\rho_{\rm c} R_{\rm c}^2}{R_{\rm c}^2 + r^2}

Bonnor-Ebert sphere

or uniform density

\rho(r) = \rho_{0}

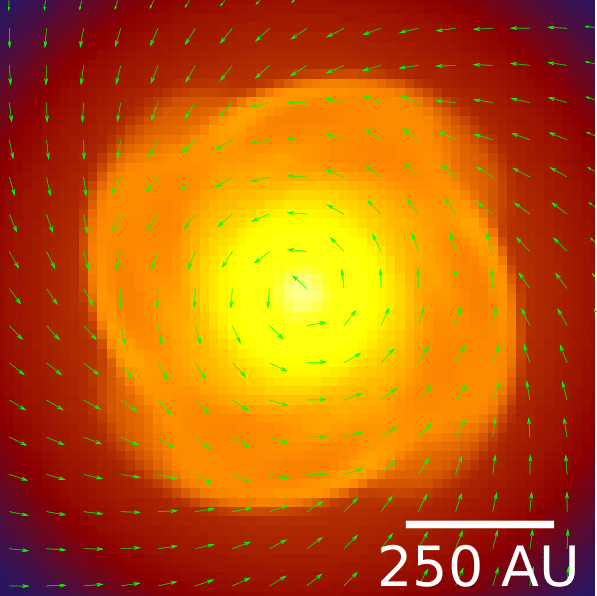
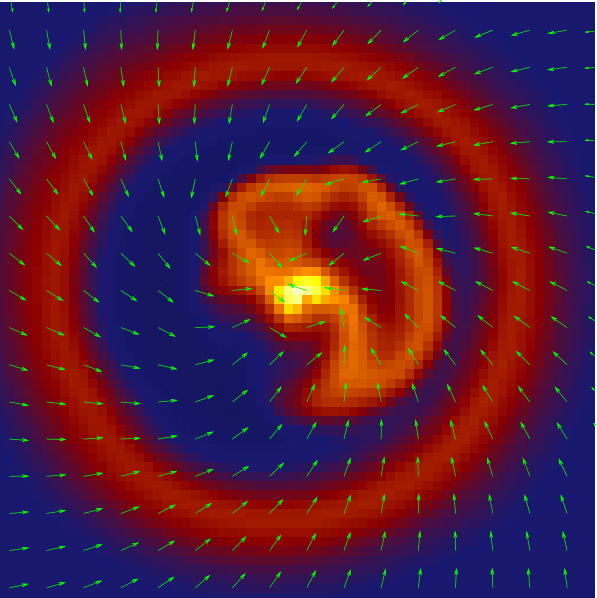
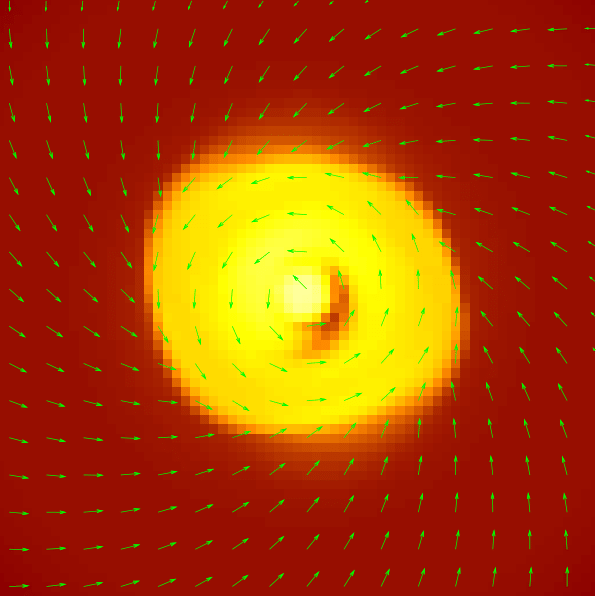
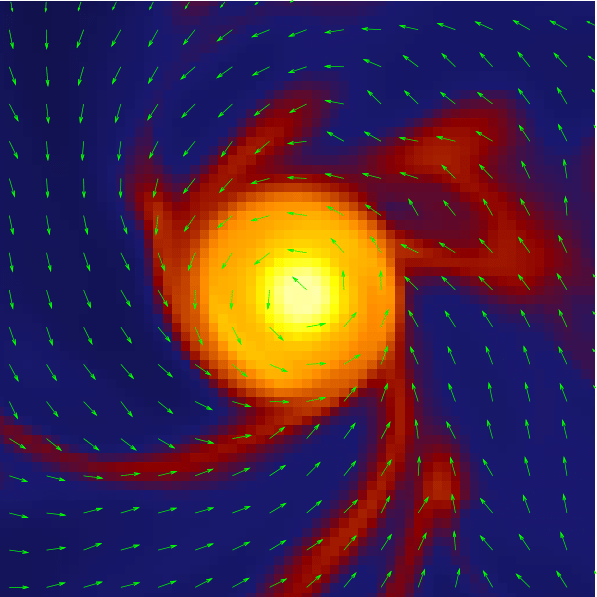
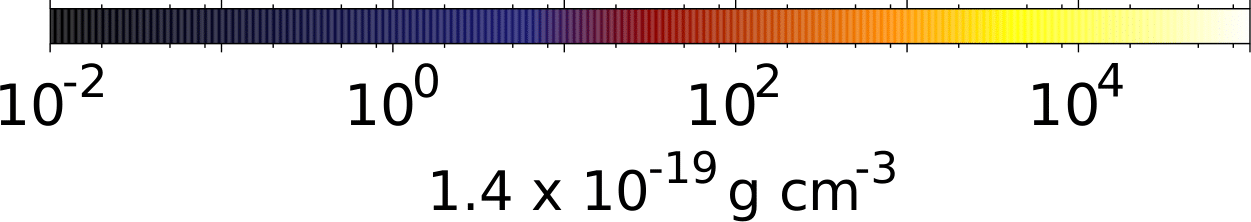
What about magnetic fields?

Help! Where is the disk?!

Ohmic, Ambipolar, Hall 

Turbulence

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

turbulence + MHD

History of modeling disk formation

for more references, see Patrick Hennebelle's talk and review articles:

Wurster & Li 2018, Zhao et al. 2020, Tsukamoto et al. 2023, Küffmeier 2024

We did learn a lot from spherical collapse models.

It is not the full picture though.

Credit: ALMA (ESO/NAOJ/NRAO)

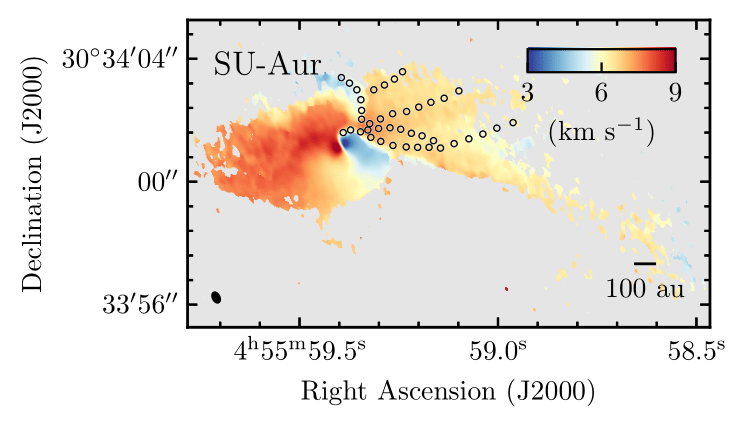
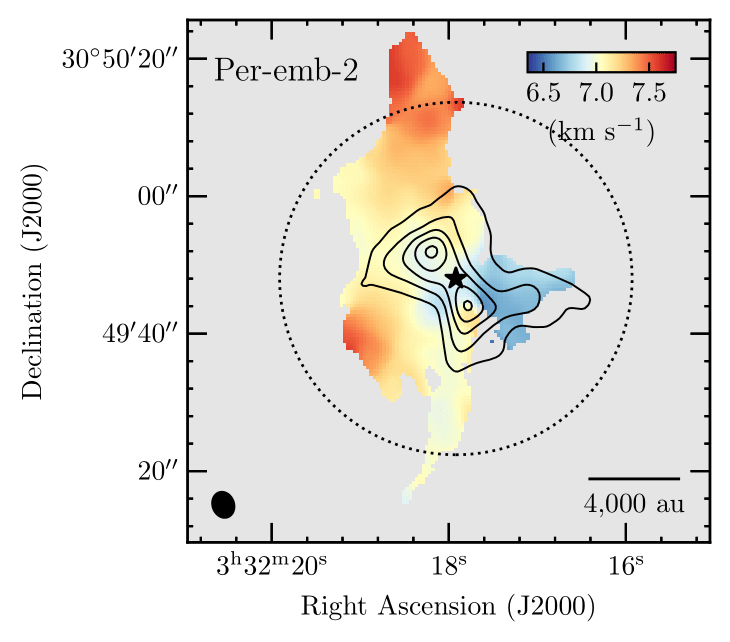
Ginski et al. 2021

Yen et al. 2019

Garufi et al. 2021

Pineda et al. 2020

50 au

BHB1 (Alves et al. 2020), GM Aur (Huang et al. 2021), IRS 63 (Podio et al. 2024, Segura-Cox in prep.), AB Aur (Grady et al. 1999 / Fukagawa et al. 2004), M512 Grant et al. 2021, Gupta et al. 2024, Cacciapuoti et al. 2024), PPVII review by Pineda et al. 2023, Antonio Garufi's talks

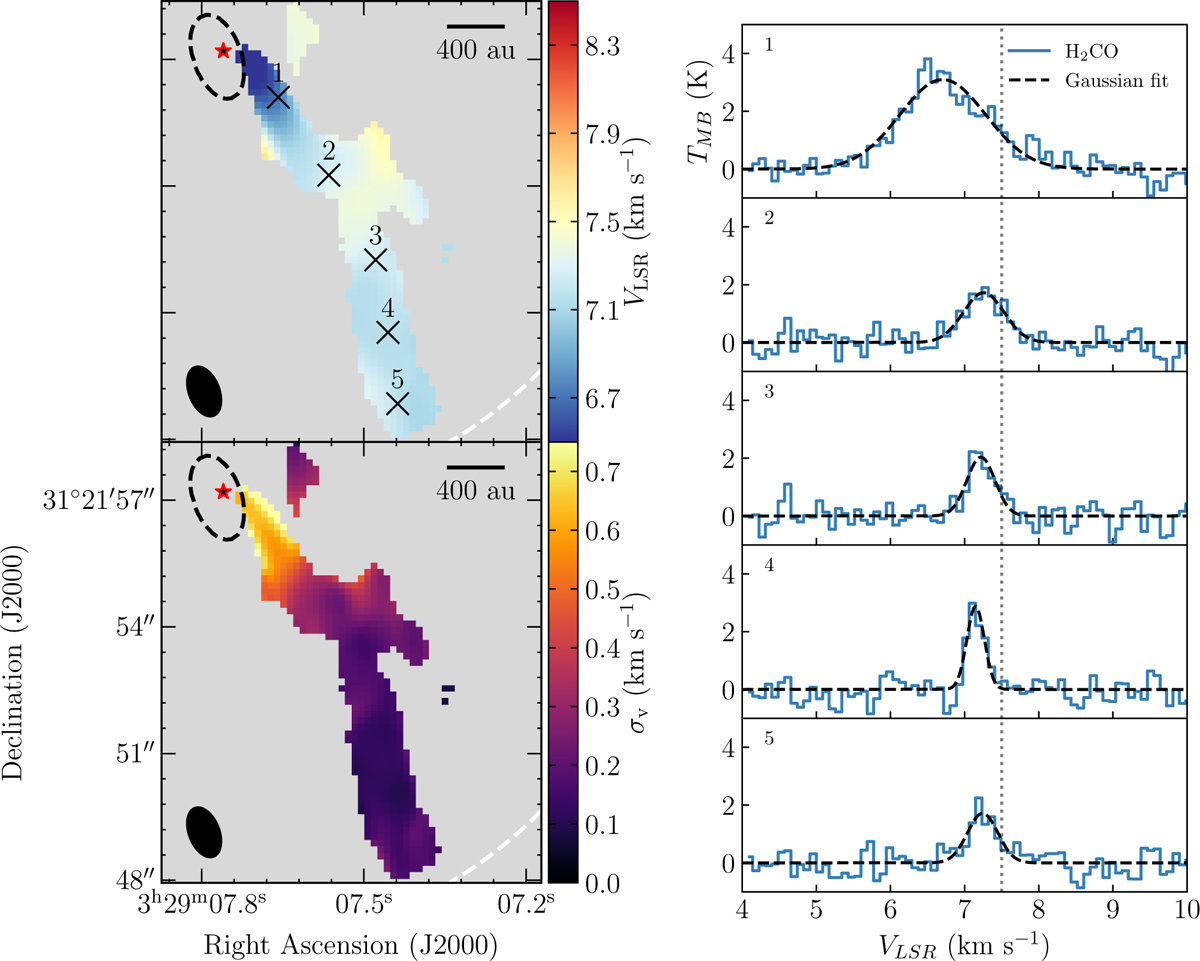
Per-emb-50

Valdivia-Mena et al. 2022 (see poster!)

Streamers:

Model star formation in a Molecular Cloud

isothermal magnetohydrodynamical (MHD) with driven turbulence

adaptive mesh refinement (AMR) simulations with RAMSES

maximum resolution: ≈25 au (level of refinement: 15), root grid about ≈1600 au (level 9)

Total mass: 3000 solar masses

periodic boundary conditions

altogether 321 sink particles at last snapshot (2 Myr after the formation of the first star)

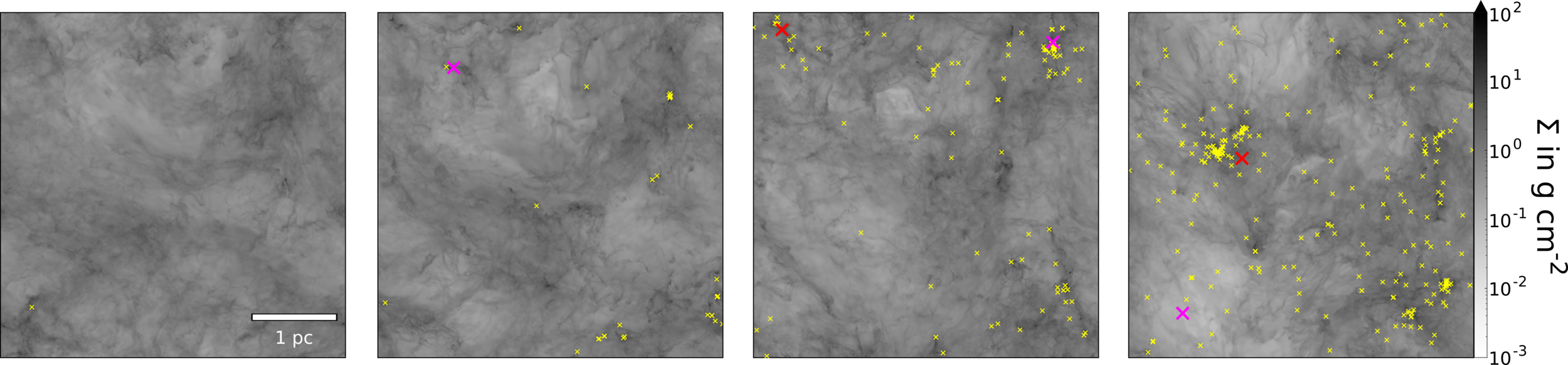
simulation setup including detailed description of sink recipe presented in Haugbølle+2018

Küffmeier, Jensen & Haugbølle '23

Two phase accretion process

Initial collapse followed by varying amount of post-collapse infall

(see also Smith+ 2011, Padoan et al. 2020, Pelkonen+ 2021)

Küffmeier, Jensen & Haugbølle '23

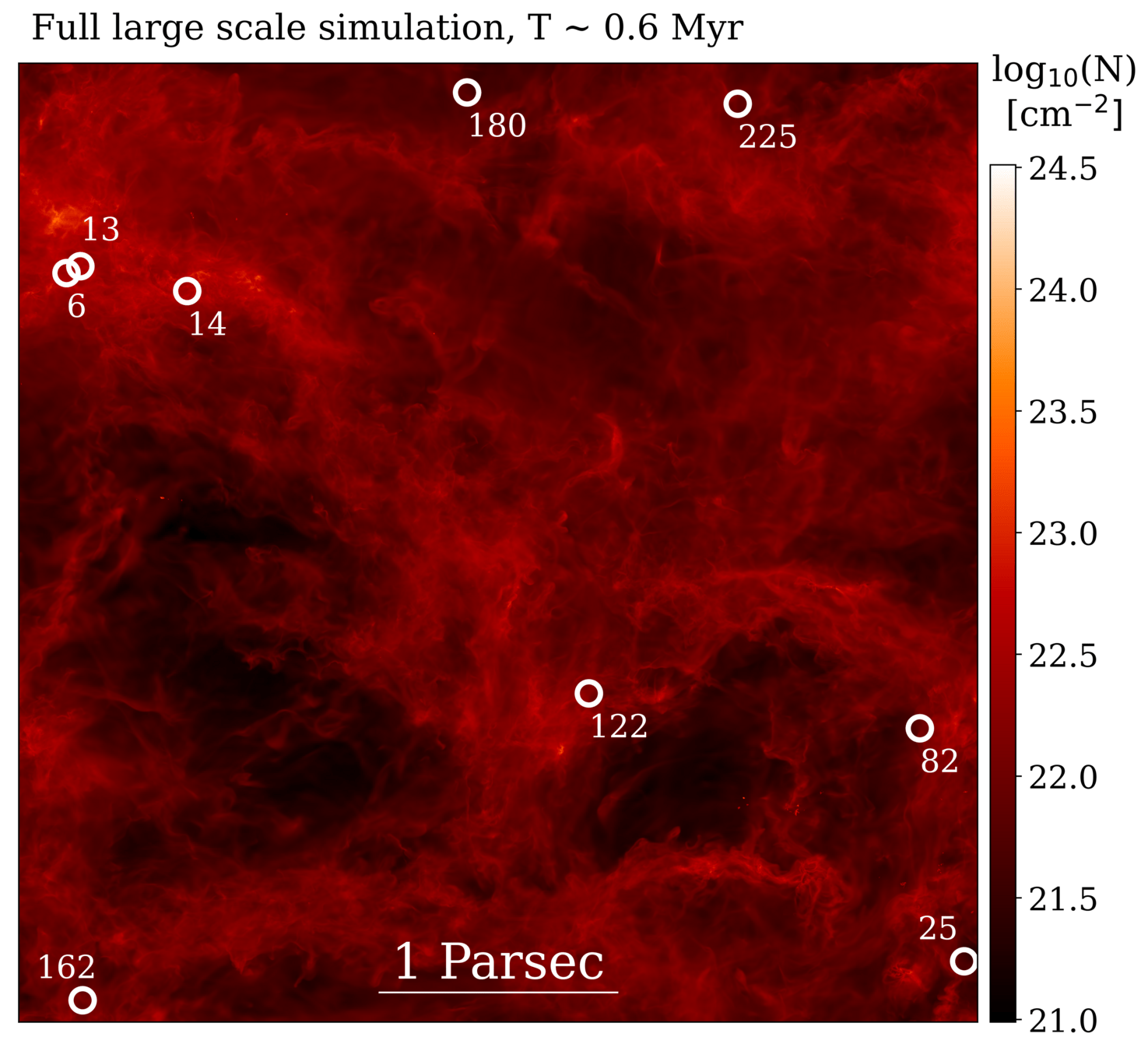
Zoom-in on early phase

The cloud

Christian G. Holm

Poster in S19

Zoom-in on the cores

Christian G. Holm

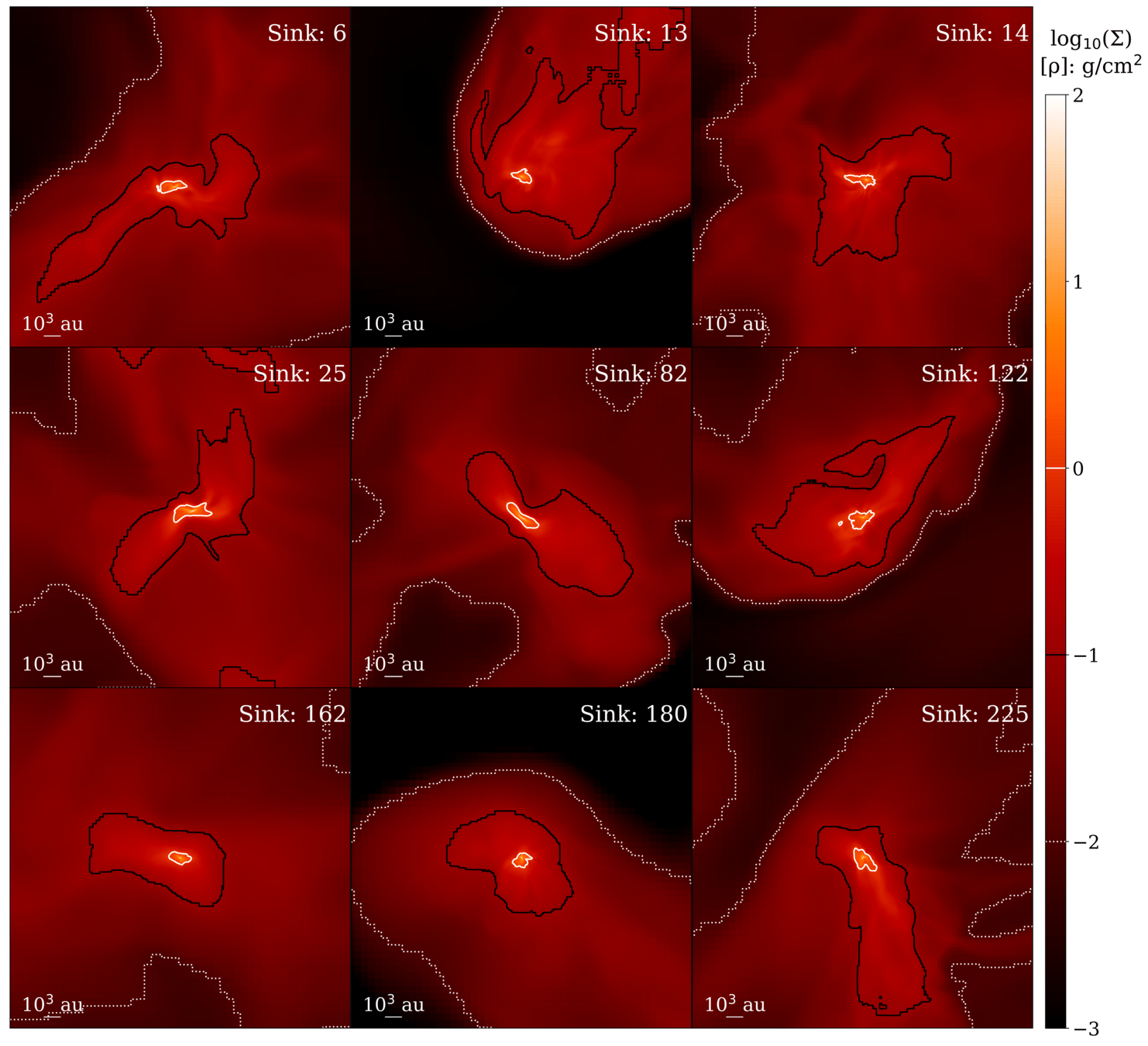
similar approach as in Küffmeier et al. 2017

How does (early) infall shape disk formation?

Christian G. Holm

Zoom-in simulation with DISPATCH, ~1 au resolution in disk, barotropic equation of state

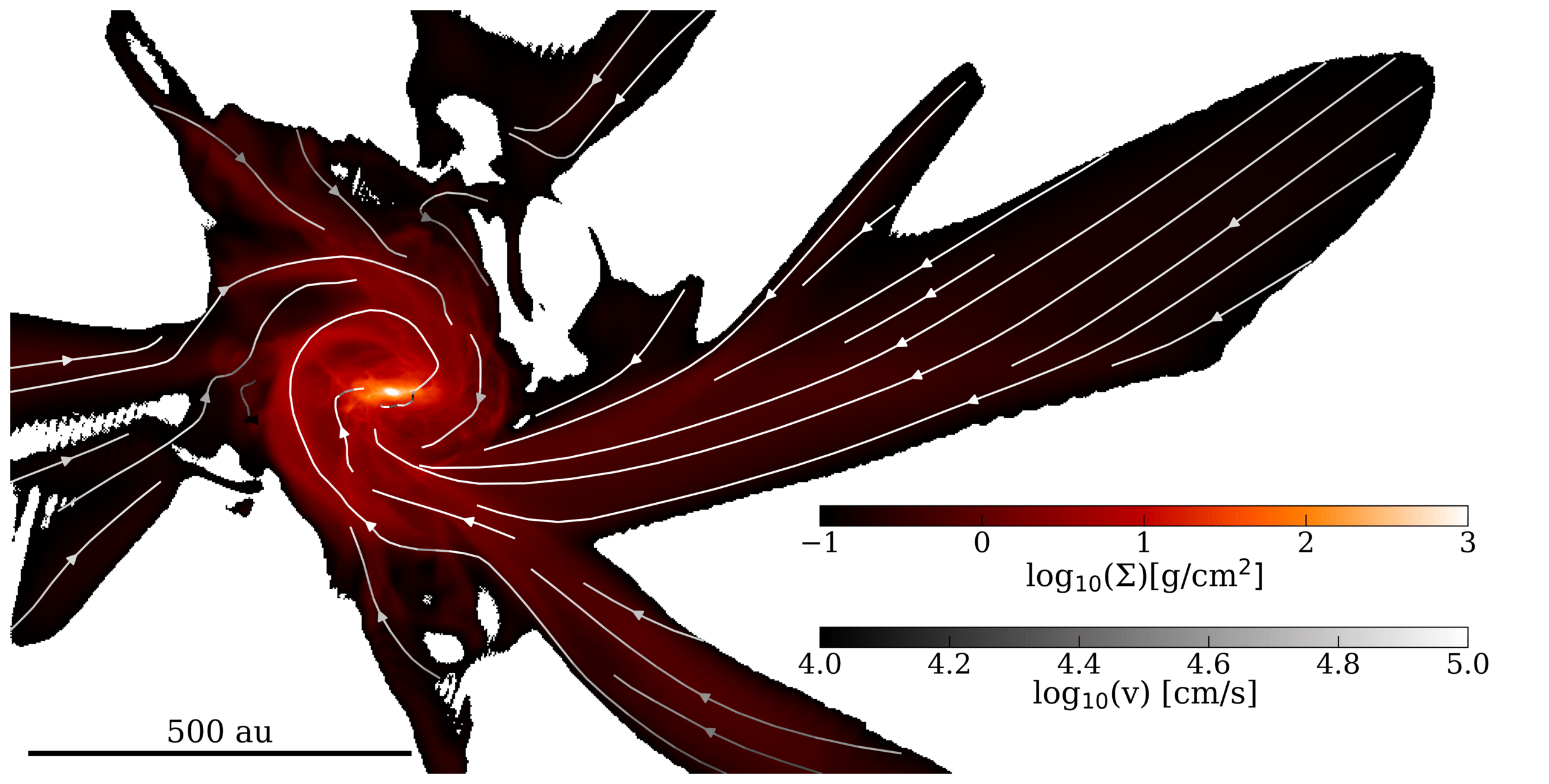
Visualizations: Berlok

Zoom-in on the forming disk

Christian G. Holm

Young embedded disks

Christian G. Holm

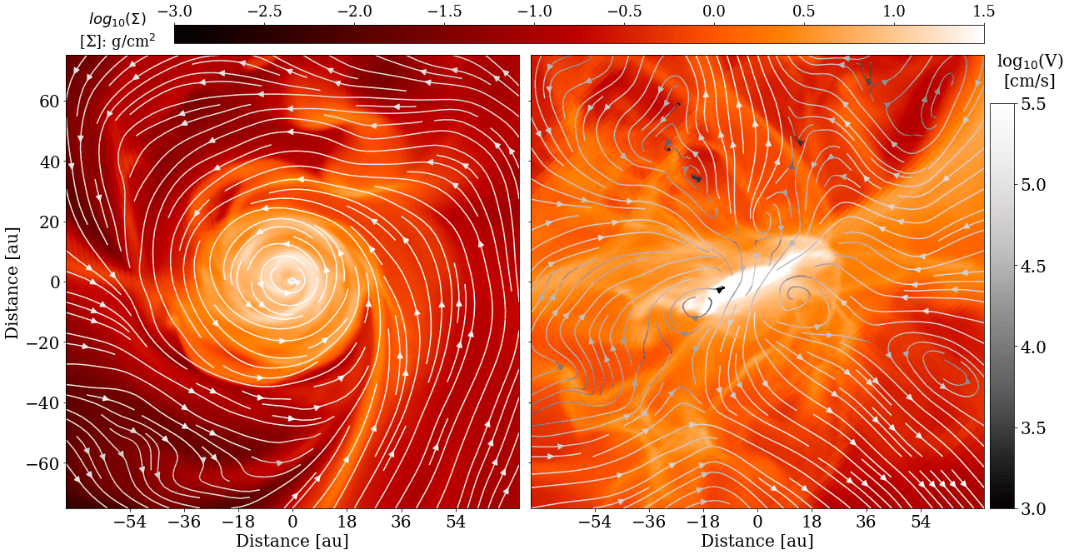
Zoom-in simulation with DISPATCH, ~1 au resolution in disk, barotropic equation of state

Poster in S19

Christian G. Holm

Infall fuels outflows

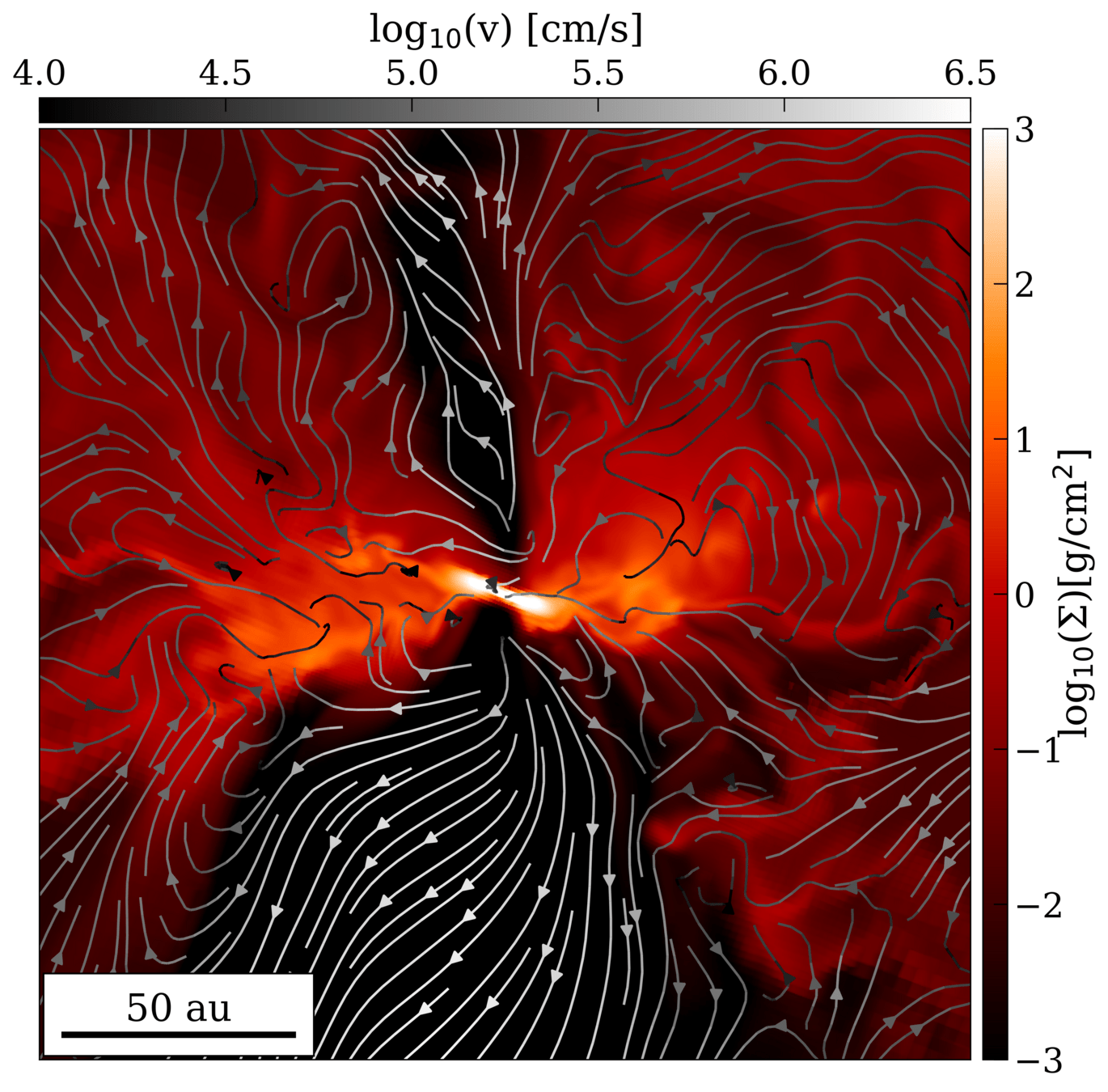
comparison of models (see also Lebreuilly et al. 2024) with observations (e.g., ALMA-DOT)

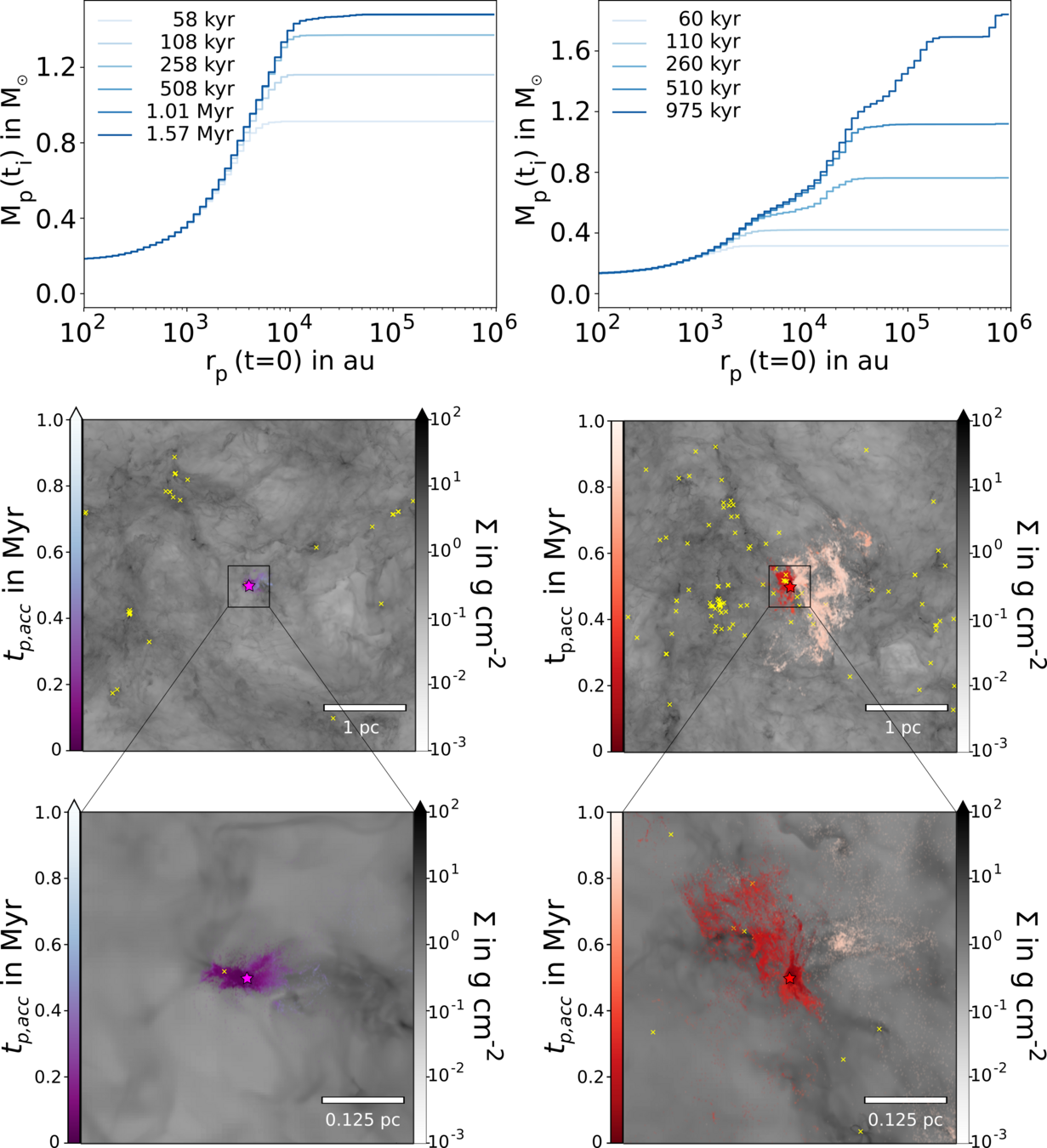
The post-collapse phase aka "late infall"

Post-collapse infall is common

On average, even solar mass stars gain ~50 % of their final mass through accretion of initially unbound material

Note that some protostars still accrete after 1.2 Myr

Küffmeier, Jensen & Haugbølle '23

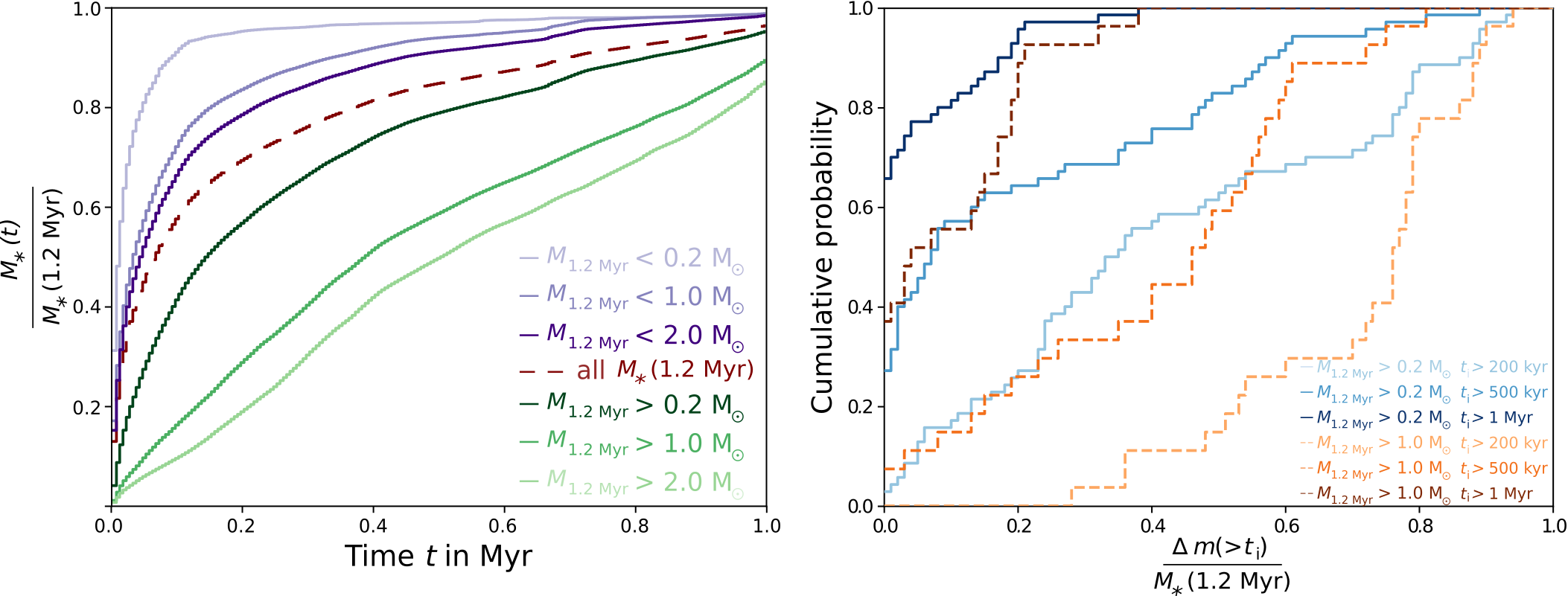
(Pelkonen et al. 2021)

YSOs can appear younger than they really are

How old is the protostar?

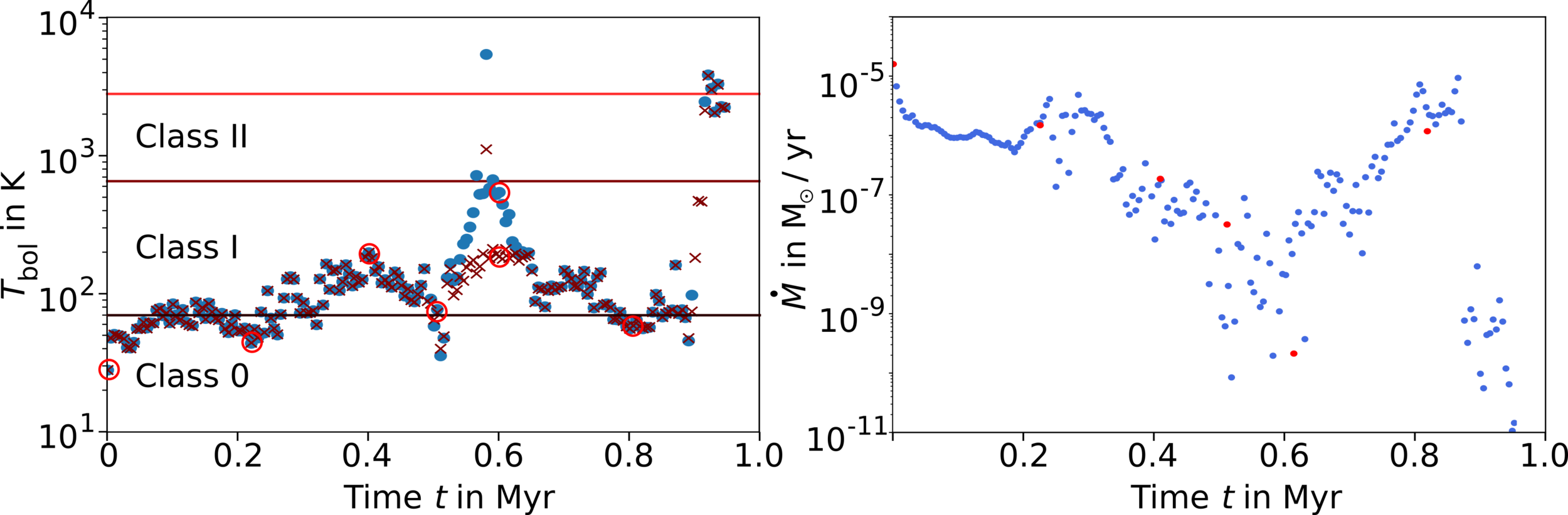
Küffmeier, Jensen & Haugbølle '23

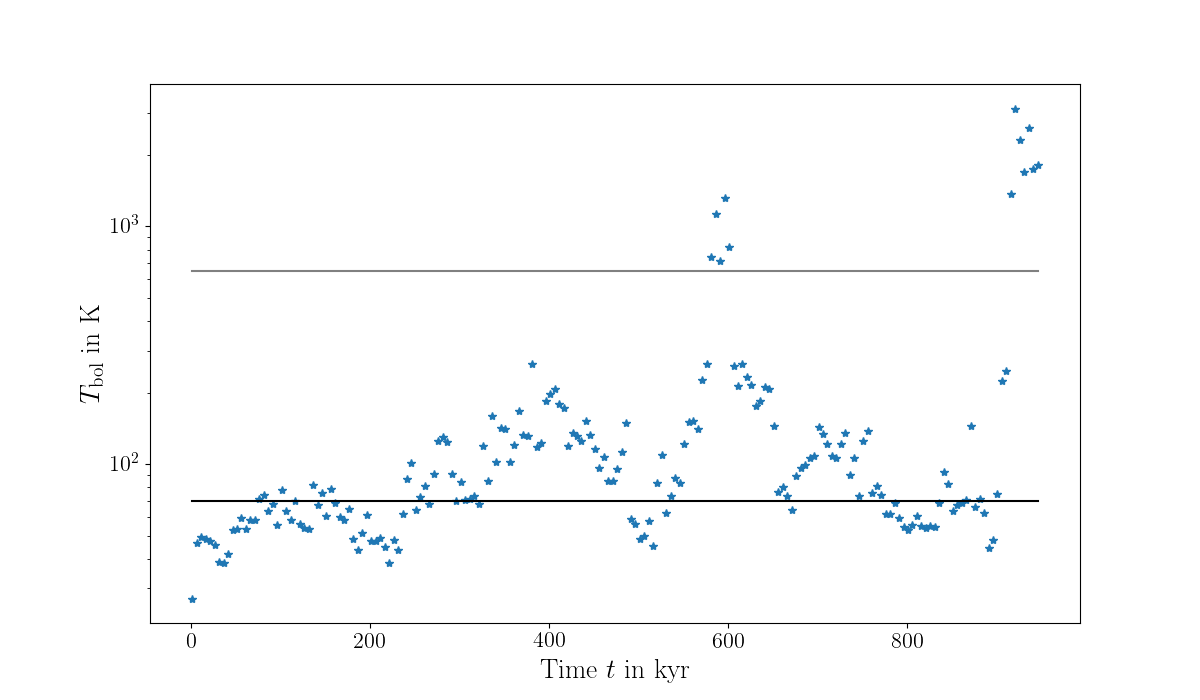
Class I

Class 0

Class II

Origin of accreting gas

"In the case of the more massive stars, accretion from the environment outside the original core volume is even more important than that from the core itself. [...]

The assumption of spherical symmetry cannot be applied to the majority of collapsing cores, and is never a good description of how stars accrete gas from outside the original core radius."

(Smith et al. 2011)

Spreading vs wind-driven?

Manara et al. 2023

Caveat!

Infall matters. Disks can easily be wind-driven and yet grow in size through infall of gas with high angular momentum.

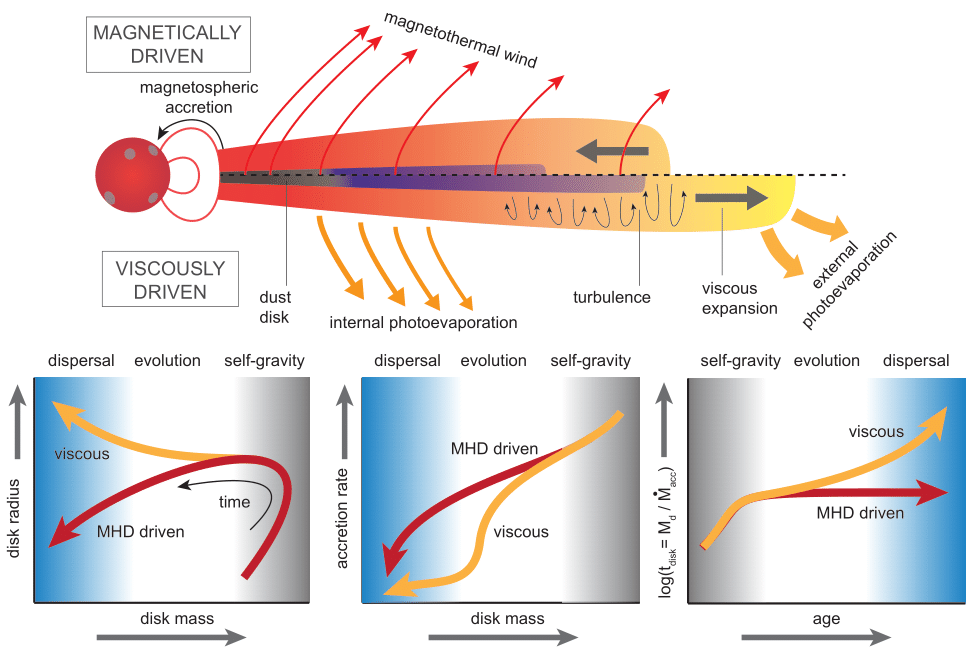
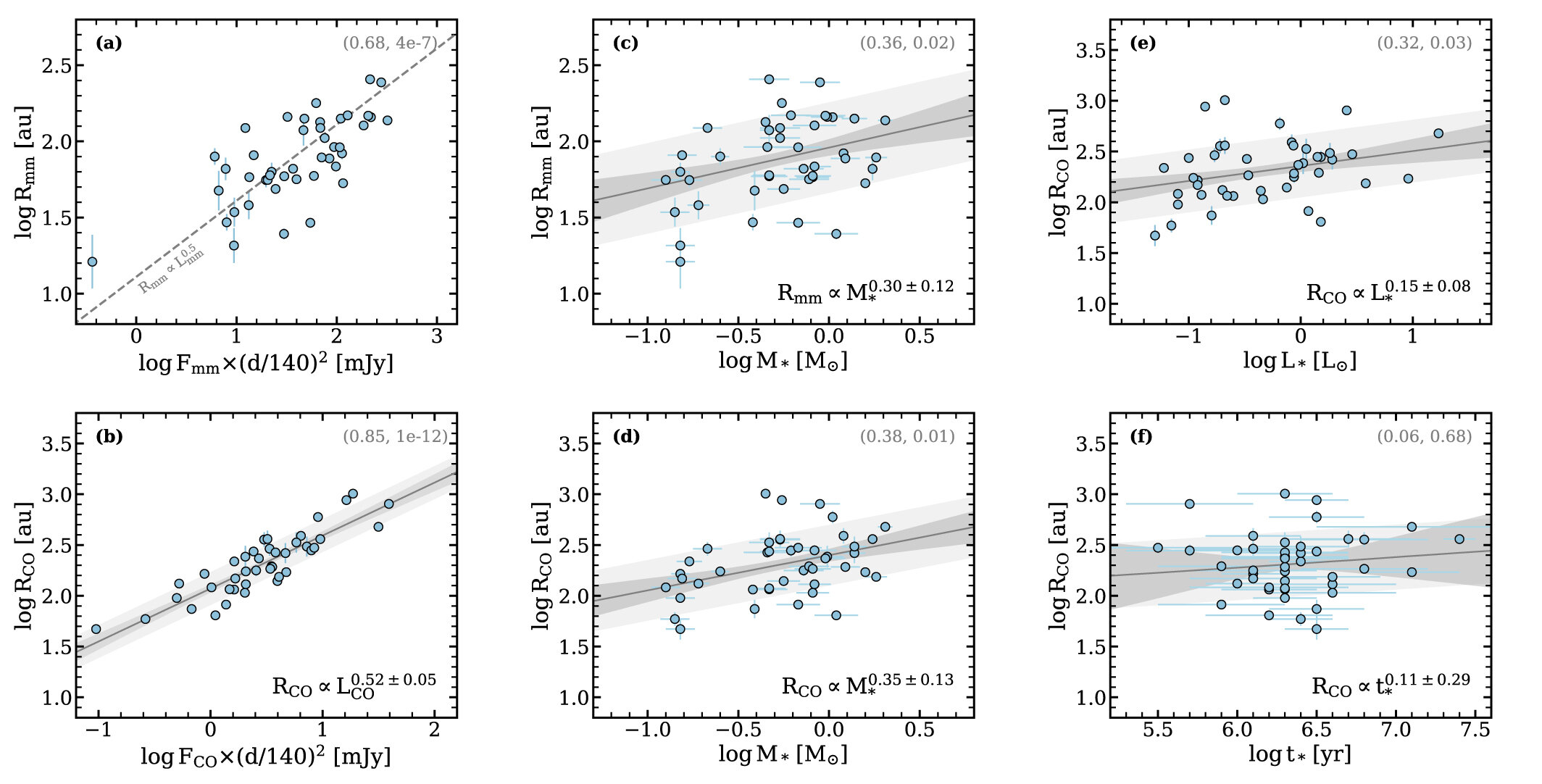
Long et al. 2022

?

Angular momentum budget

  • Large scatter of ang. mom.
  • Increasing specific angular momentum for increasing final stellar mass

Specific angular momentum computed from all accreting tracer particles at the first snapshot after star formation

  • subtle correlation with mass (inherited by disks?), important for WG7 (Miguel Vioque's talks)

"We find marginal relationships between disk sizes and M*." (Long+ 2022)

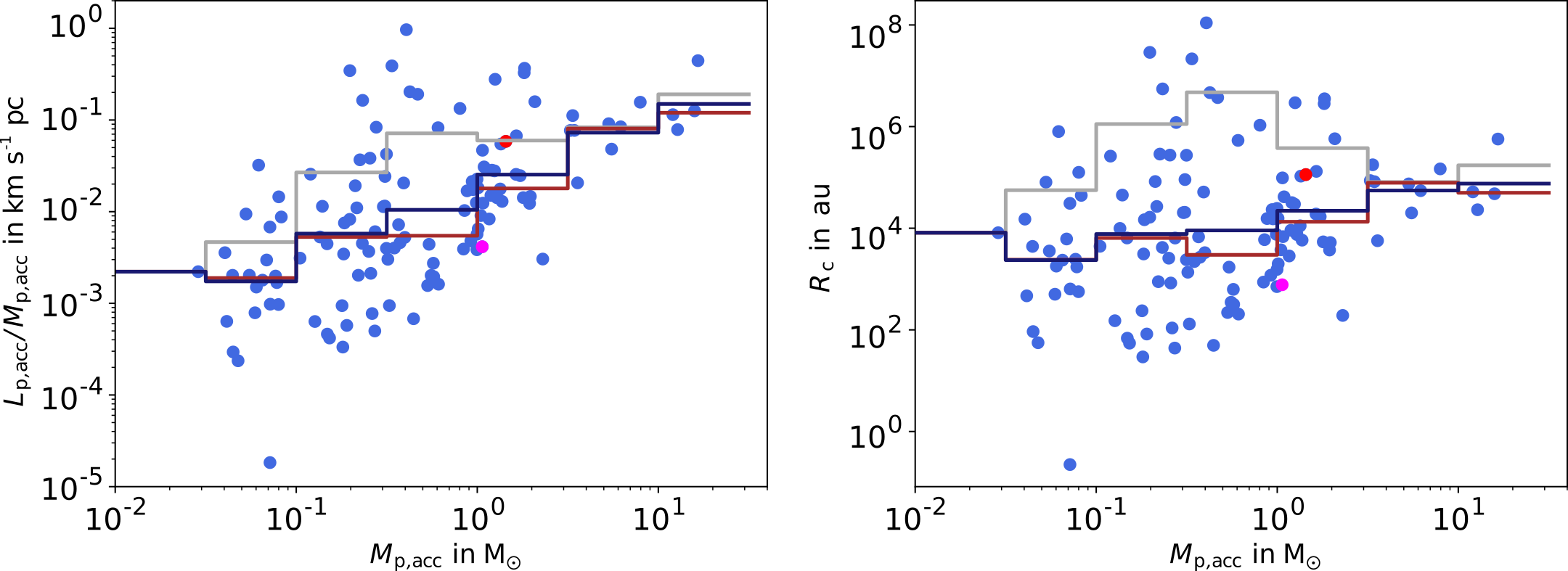
Küffmeier, Jensen & Haugbølle 2023

Long et al. 2022

see also recent papers by Padon et al. 2024, Winter et al. 2024

On average, stars with increasing final mass undergo prolonged infall

Orientation of star-disk systems can change substantially

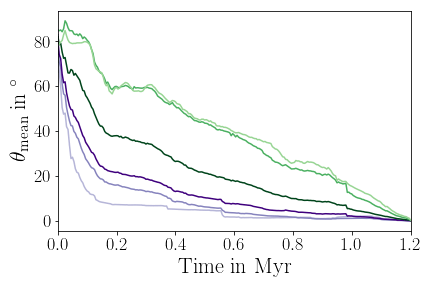
Orientation of infall

Küffmeier, Haugbølle, Pineda & Segura-Cox 2024

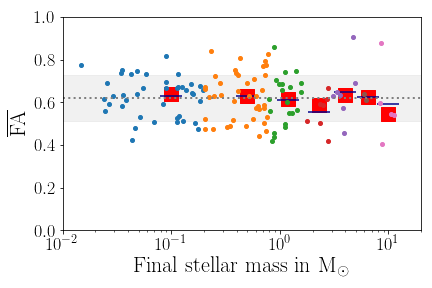
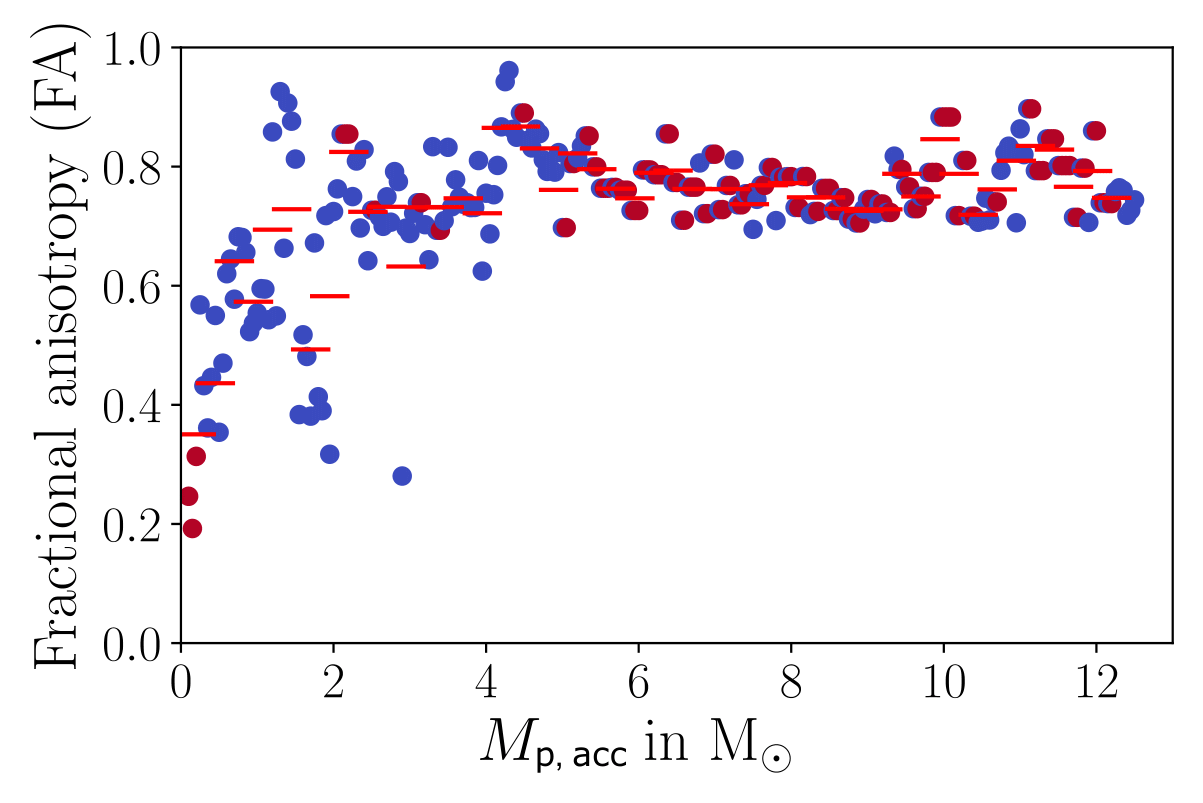
How to quantify anisotropy of accretion?

FA = 0: perfectly isotropic accretion

FA = 1: maximally anisotropic accretion

Küffmeier, Haugbølle, Pineda & Segura-Cox 2024

Fractional anisotropy based on tracer particles

Post-collapse infall is more anisotropic than initial collapse

Post-collapse accretion phase resembles Bondi-Hoyle

Post-collapse infall is more anisotropic than initial collapse

Anisotropic accretion

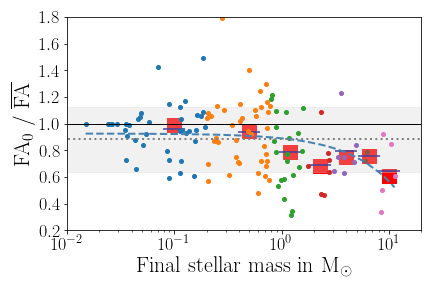
FA = 0: perfectly isotropic accretion

FA = 1: maximum anisotropic accretion

Küffmeier, Haugbølle, Pineda & Segura-Cox 2024

Late infall is more anisotropic than early collapse

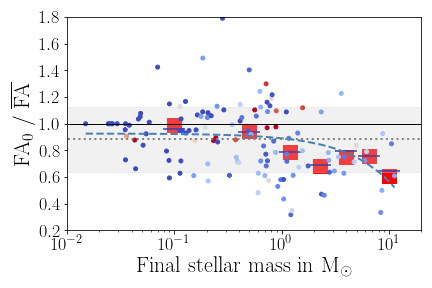
\mathrm{FA} = \sqrt{ \frac{1}{2}} \frac{\sqrt{(\lambda_1 - \lambda_2)^2 + (\lambda_2 - \lambda_3)^2 + (\lambda_3 - \lambda_1)^2}}{\sqrt{\lambda_1^2 + \lambda_2^2 + \lambda_3^2}}

Fractional anisotropy (FA) serves as a good measure for the (an-)isotropy of accretion.

FA=0: perfectly isotropic accretion, FA=1: maximally anisotropic

\frac{\Delta t_{\rm single}}{\Delta t_{\rm single}+\Delta t_{\rm mult}}
1
0

FA can also be a useful measure to compare (an)isotropy of stellar spins in clusters 

Streamers (and shadows) as signs of infall

Formation of misaligned configuration

Observable as shadows in outer disk

Küffmeier, Dullemond, Reissl & Goicovic 2021

SU Aur (Ginski et al. 2021)

300 au

Krieger, Küffmeier et al. 2024

Do we really know disk "lifetimes"?

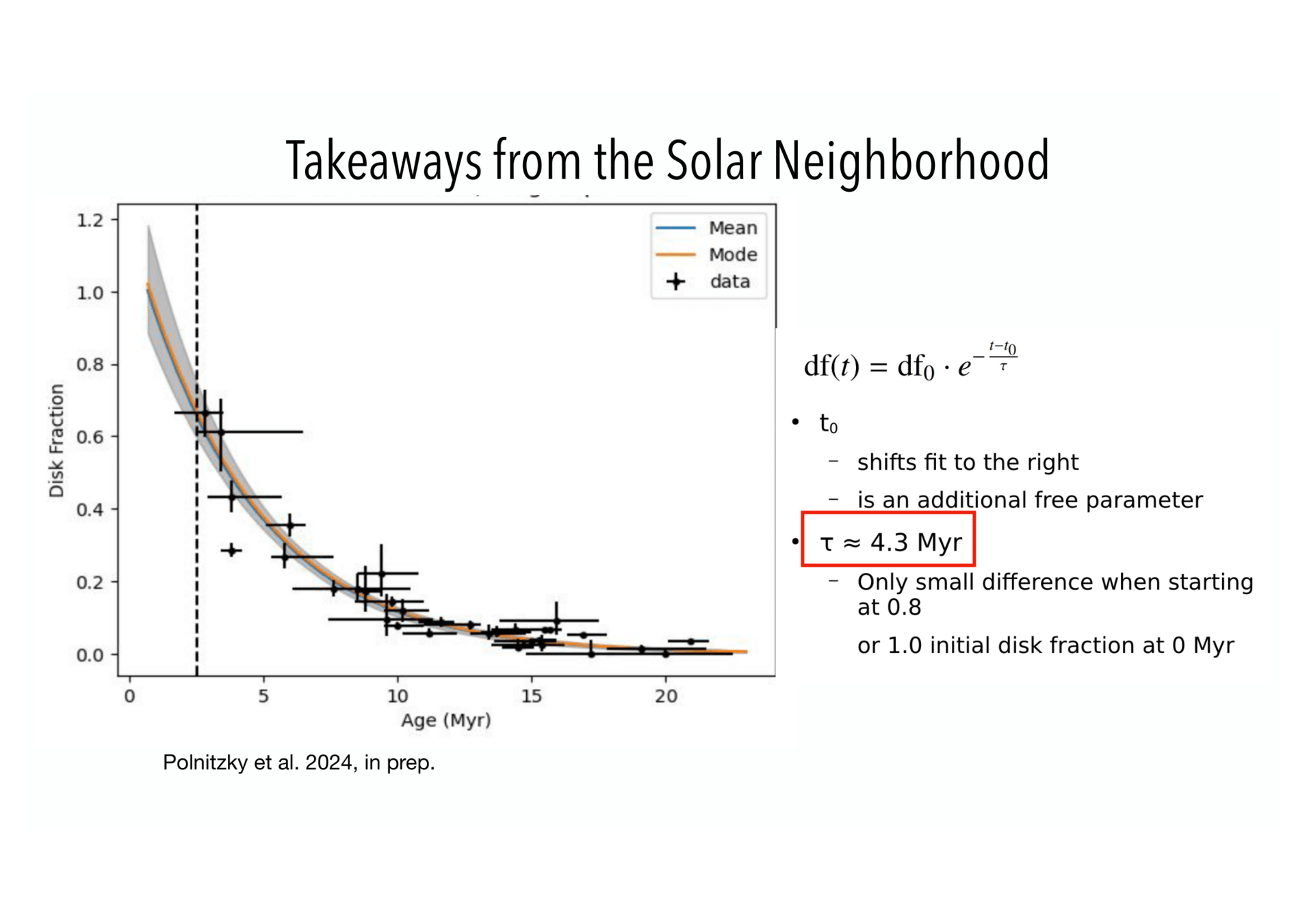
Polnitzky et al. 2024 in prep

Fraction reflecting occurrence of infall events instead of disk age?

Summary

Disks are replenished, distorted or even destroyed by misaligned infall

Protostellar environment and multiplicity matters 

Star formation is a two-phase process consisting of mandatory initial collapse and post-collapse infall phase

Küffmeier 2024, credit: Lützen

(although barely covered in this talk)

Planet-forming disks are not isolated entities

  • Is the disk solely replenished with fresh material?
  • Does infall frequently lead to the formation of a new misaligned outer disk (and if yes, for how long)?
  • Is (late) infall catastrophic? Does a completely new disk form?

Some questions to be addressed in upcoming work

Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

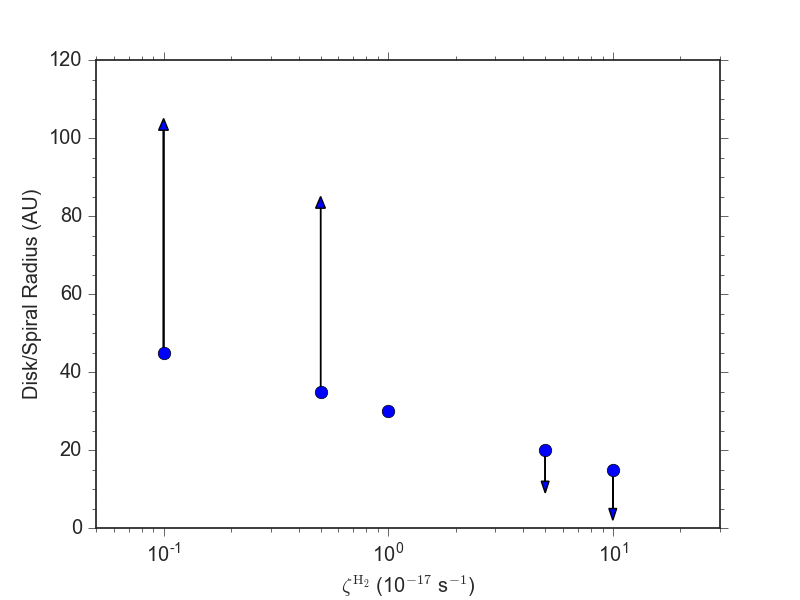
see also Wurster et al. 2018

Küffmeier, Zhao & Caselli 2020

What fraction of the gas and dust returns to the disk after being ejected by an outflow?

Key question

Credit: Tsukamoto et al. 2021

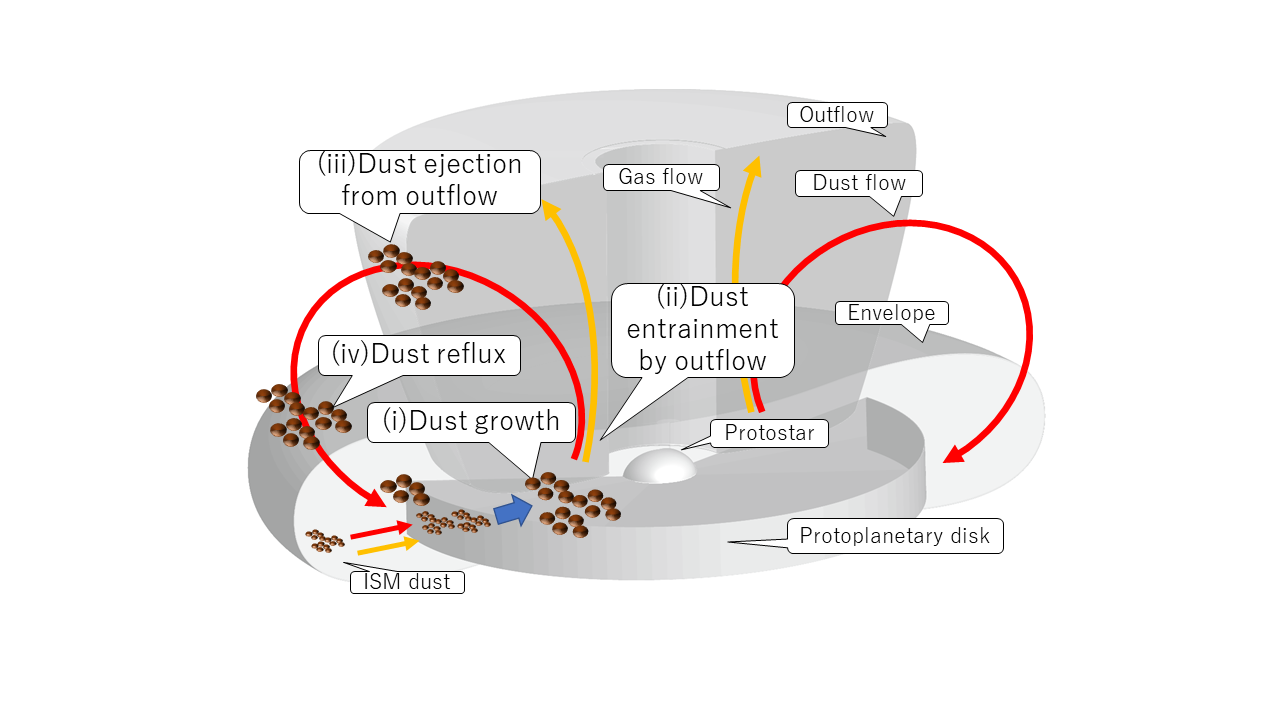
"Ash-fall" scenario aka conveyor belt

Increase in dust-to-gas ratio because dust can grow in disk and return

Tsukamoto et al. 2021

Zoom-in on embedded stars

Küffmeier et al.

2019

Küffmeier et al. 2018

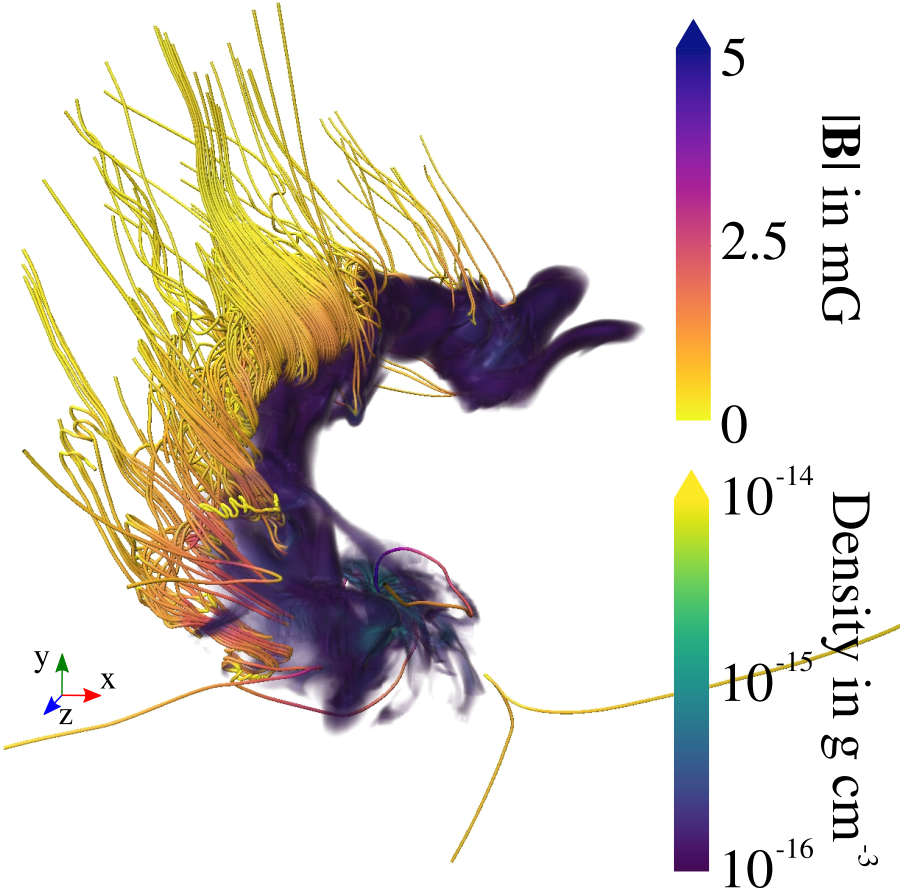
Küffmeier, Reißl et al. 2020

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

~1500 AU

Pro: self-consistent initial and boundary conditions for star formation

Con: computationally more expensive, more difficult analysis

for a similar concept, see also Lebreuilly et al. 2024

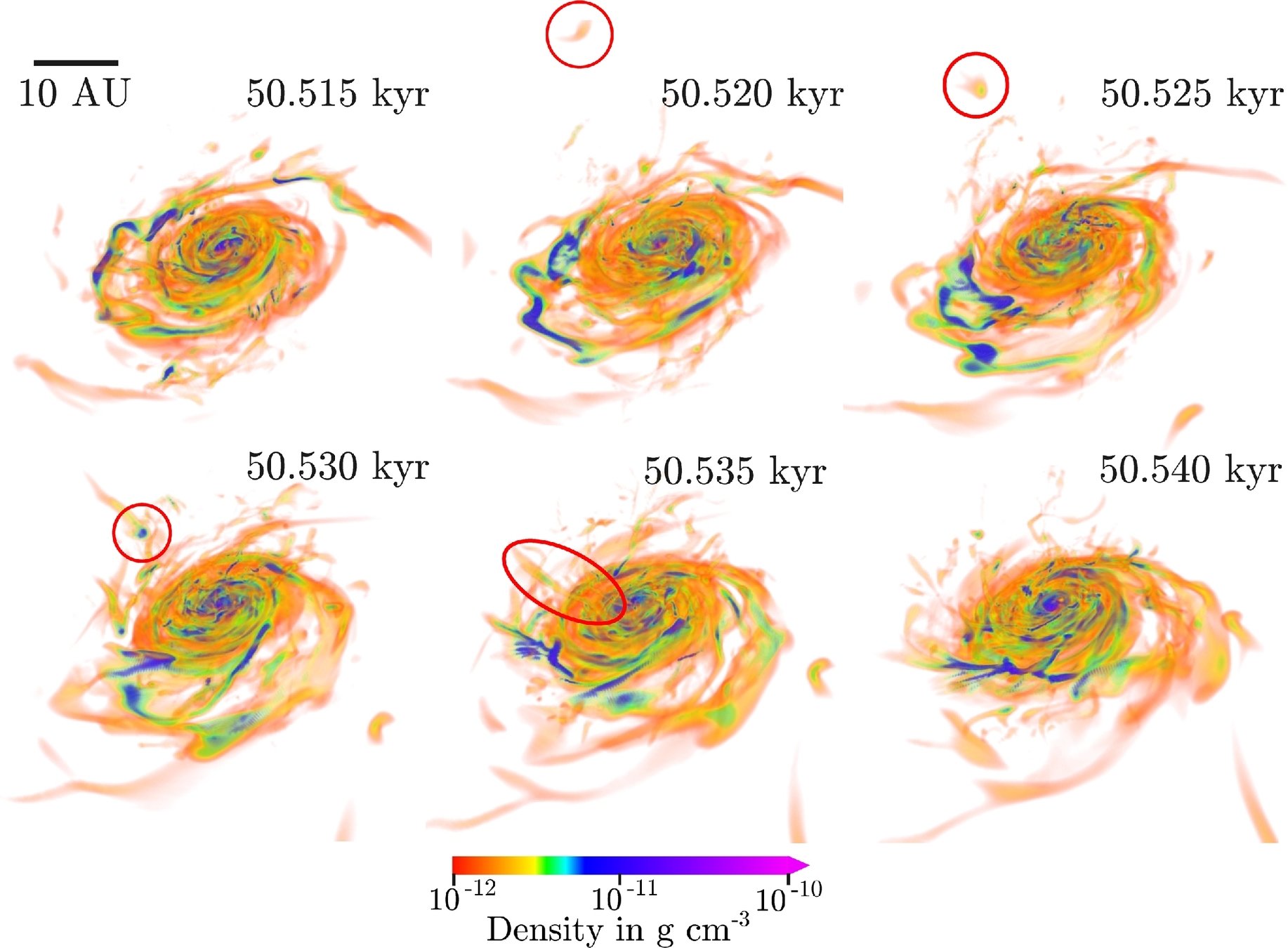
Christian G. Holm

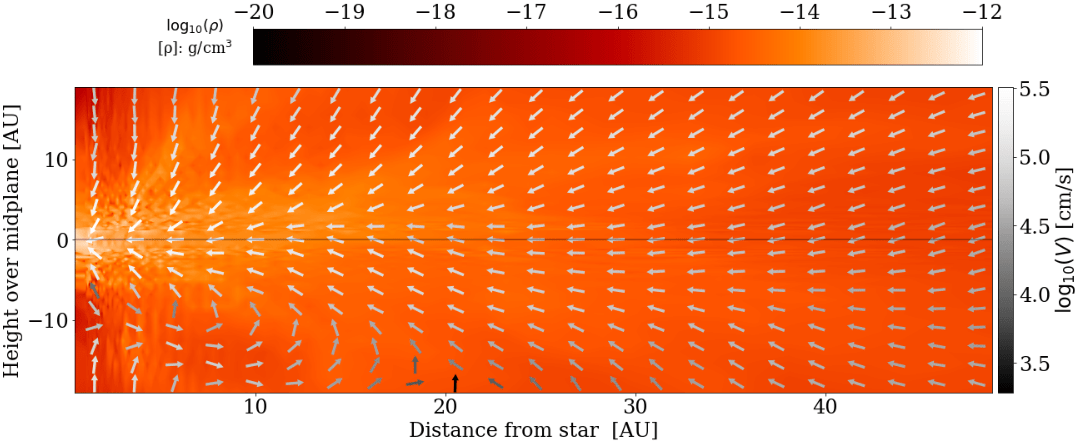
star A, t = 13 kyr

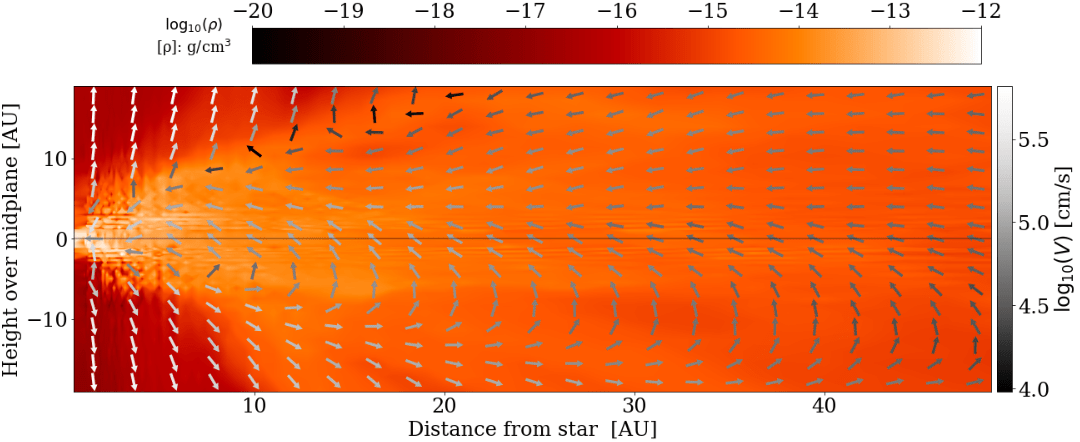
star A, t = 25 kyr

strong magnetic braking,

strong outflow

Gas accretes through the disk (little polar accretion)

Christian G. Holm

How do outflows affect disk formation?

star A, t = 13 kyr

star A, t = 25 kyr

strong magnetic braking,

strong outflow

Prospect to compare with observations of outflows (e.g., ALMA-DOT, PI: Podio)

Credit: NASA/ESA Hubble space telescope &

ALMA (ESO/NAOJ/NRAO)

The big challenge:

link planet to star formation

50 au

Implications for Al-26 heterogeneity

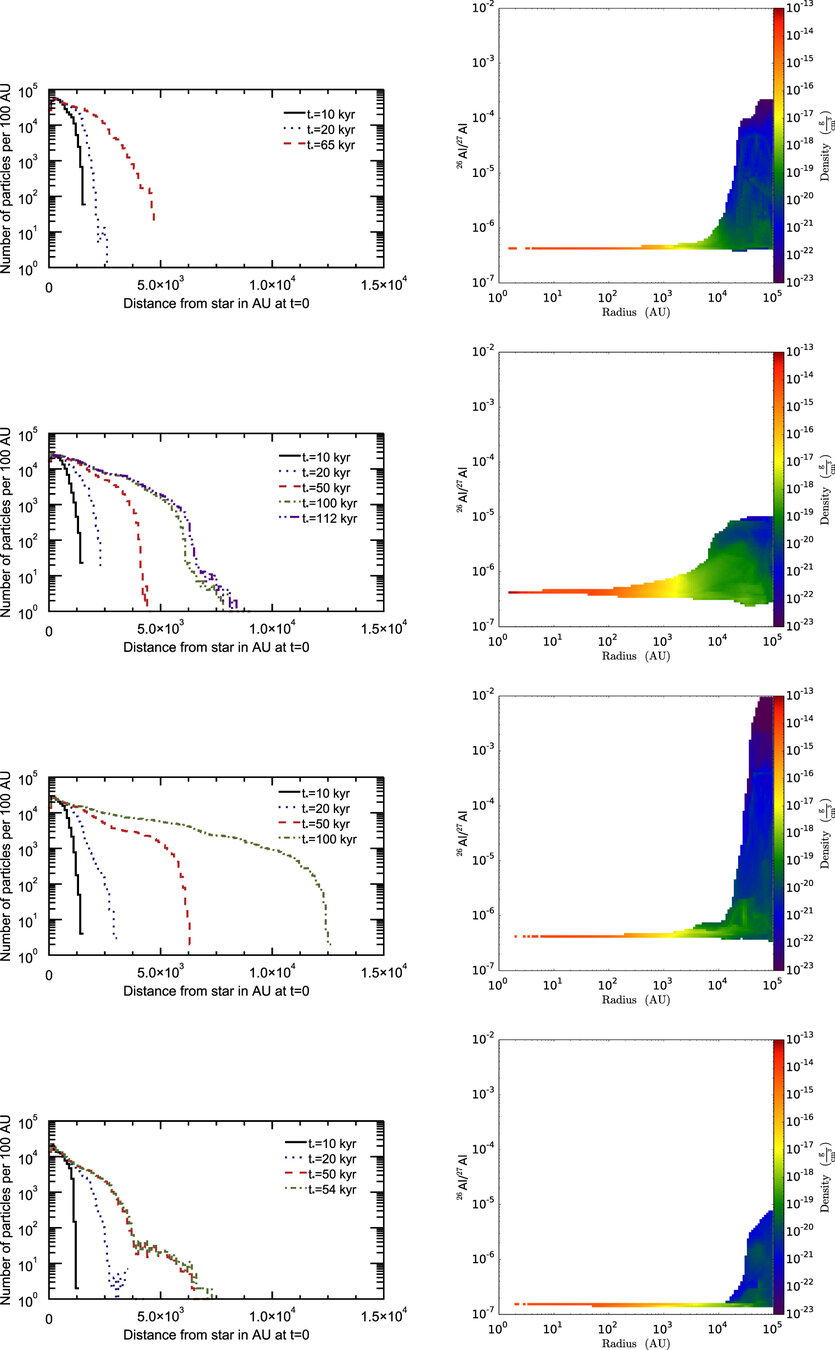
Küffmeier et al. 2016

  • Gas is well-mixed within core, and hence Al-26 abundance is fixed during CAI formation (t<~100 kyr).
  • BUT: significant deviations in Al-26 abundance beyond the core may likely be imprinted on disk afterwards!

Christian G. Holm

How do infall and outflow affect the disk?

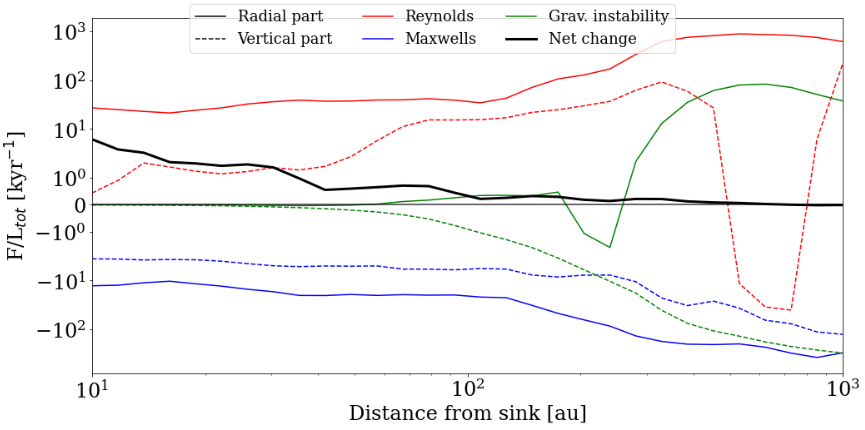
Angular momentum transport via magnetic braking

Zoom-in on embedded protostars

Küffmeier, Calcutt & Kristensen 2019

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

Küffmeier, Reißl et al. 2020

~1500 AU

Küffmeier et al. 2018

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]
\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal