Michael Küffmeier (Carlsberg reintegration fellow)

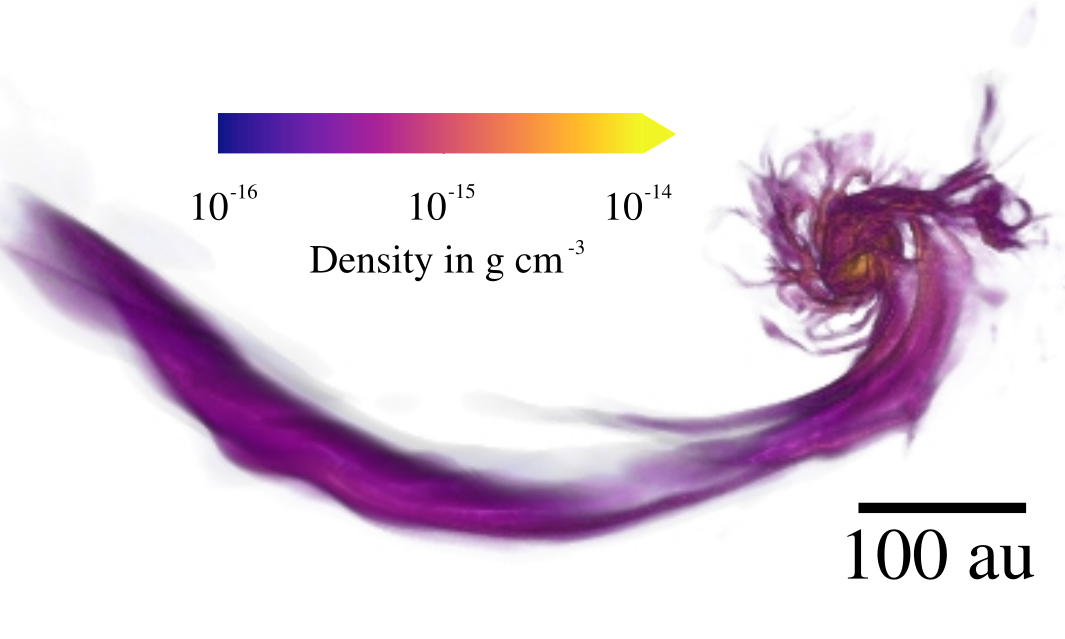
Revisiting star-disk formation in their birth environments

Sigurd Jensen, Jaime Pineda, Paola Caselli (MPE), Christian G. Holm, Troels Haugbølle (NBI), Stefan Reißl, Kees Dullemond (ITA)

Let's go back in time to the year 2014

Wow!

Credit: ALMA (ESO/NAOJ/NRAO)

Credit:

DSHARP team

10 au

50 au

The classical picture

credit: M. Persson

star formation

planet formation

History of modeling disk formation

spherical core collapse:

rotation

magnetization (mass-to-flux ratio)

non-ideal MHD effects

dust evolution

turbulence

useful for parameter studies

\rho(r) = \frac{\rho_{\rm c} R_{\rm c}^2}{R_{\rm c}^2 + r^2}

Bonnor-Ebert sphere

or uniform density

\rho(r) = \rho_{0}

History of modeling disk formation

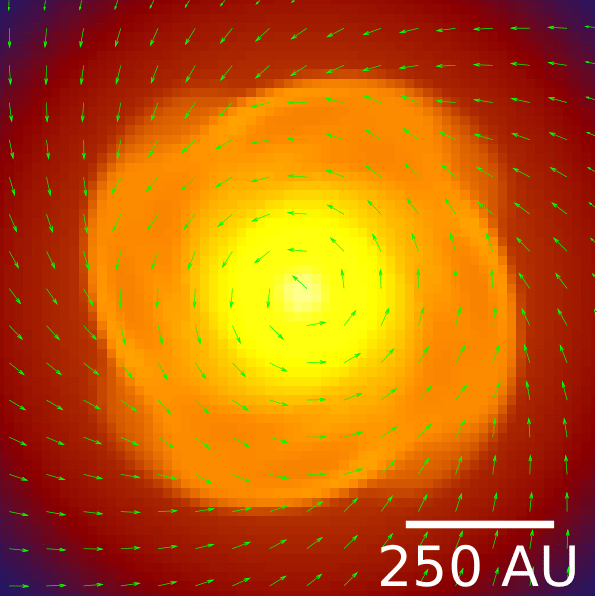
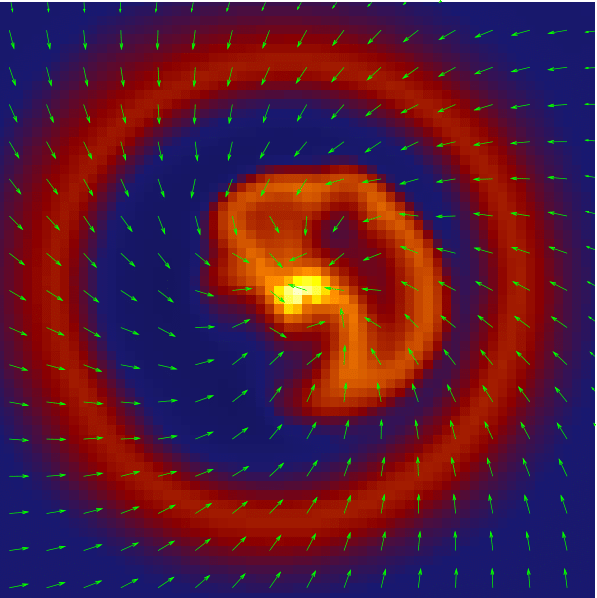
What about magnetic fields?

Help! Where is the disk?!

Santos-Lima et al. 2012

Hydro

ideal MHD

L_{\rm mag} = \int_{t_{\rm c}}^{t}\int^V r (\mathbf{J} \times \mathbf{B})_\phi \mathrm{d}V\mathrm{d}t

Magnetic braking catastrophe

Angular momentum is transported too efficiently away from the disk

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]
\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal

Non-ideal MHD

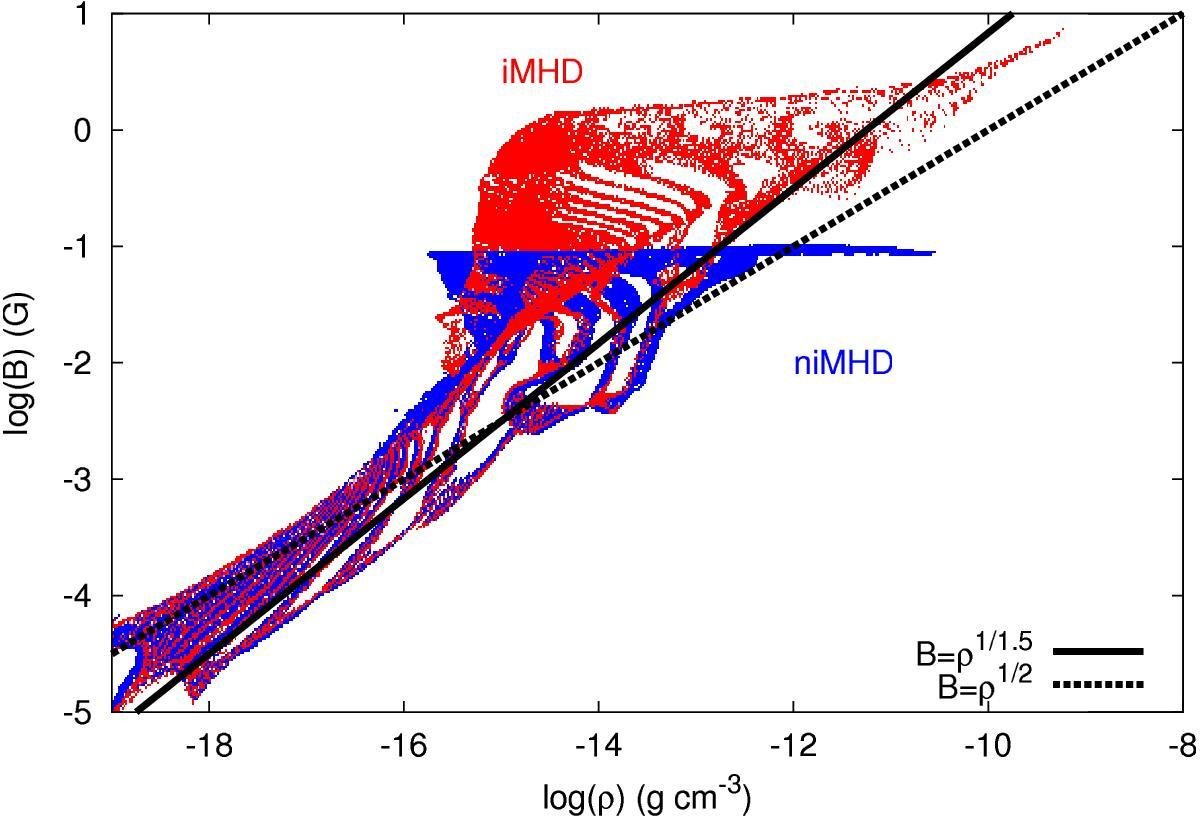
Masson et al. 2016

resistivities quench pile-up of magnetic field 

avoids magnetic braking catastrophe

see Hennebelle et al. 2016 or Lee et al. 2021 for analytical studies

more references in reviews by Wurster & Li 2018 and Tsukamoto et al. 2023

History of modeling disk formation

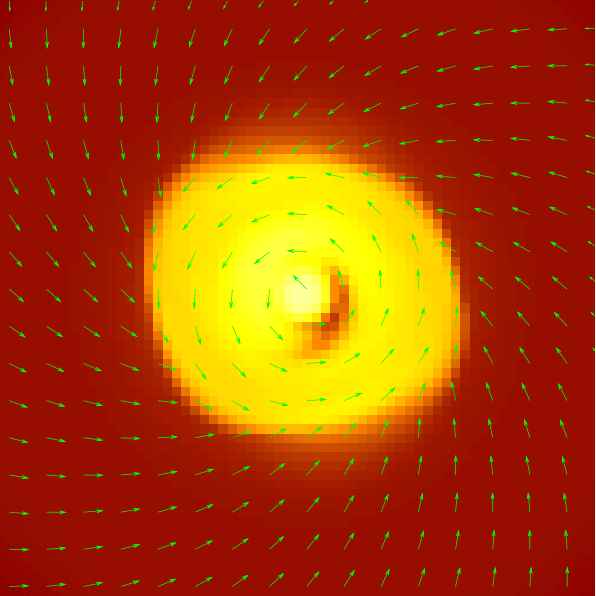
What about magnetic fields?

Help! Where is the disk?!

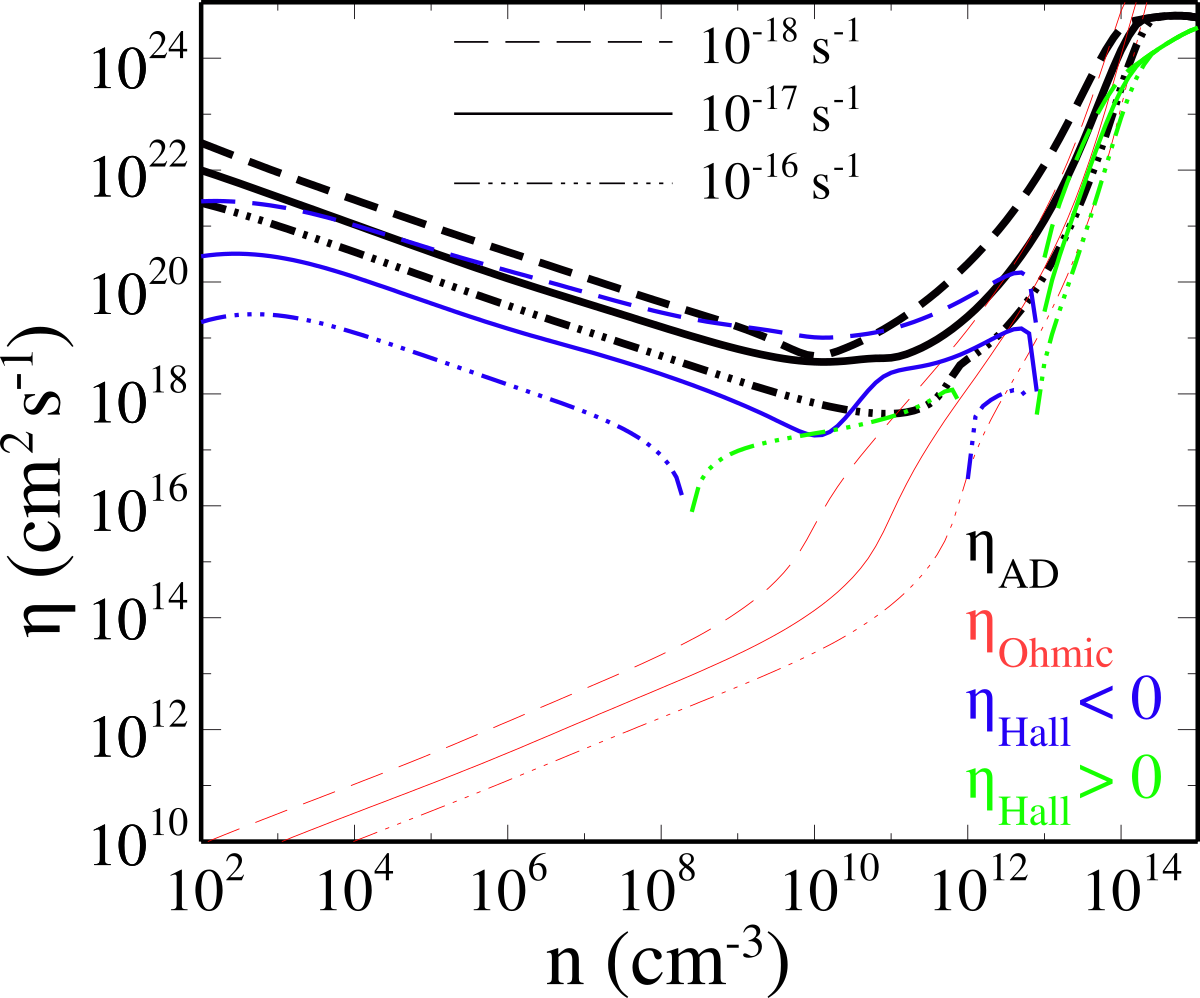
Ohmic, Ambipolar, Hall 

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

non-ideal MHD is not a single parameter that is turned on or off

Achtung!

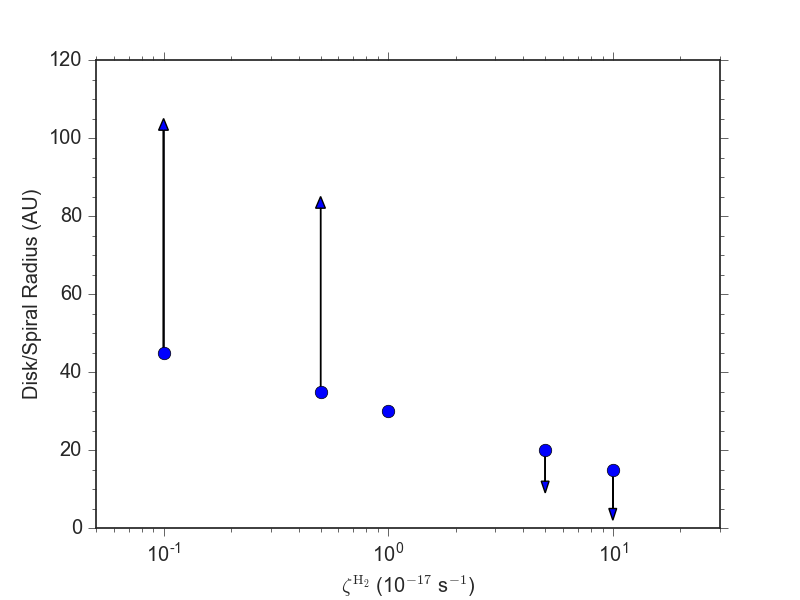
Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

Küffmeier, Zhao & Caselli 2020

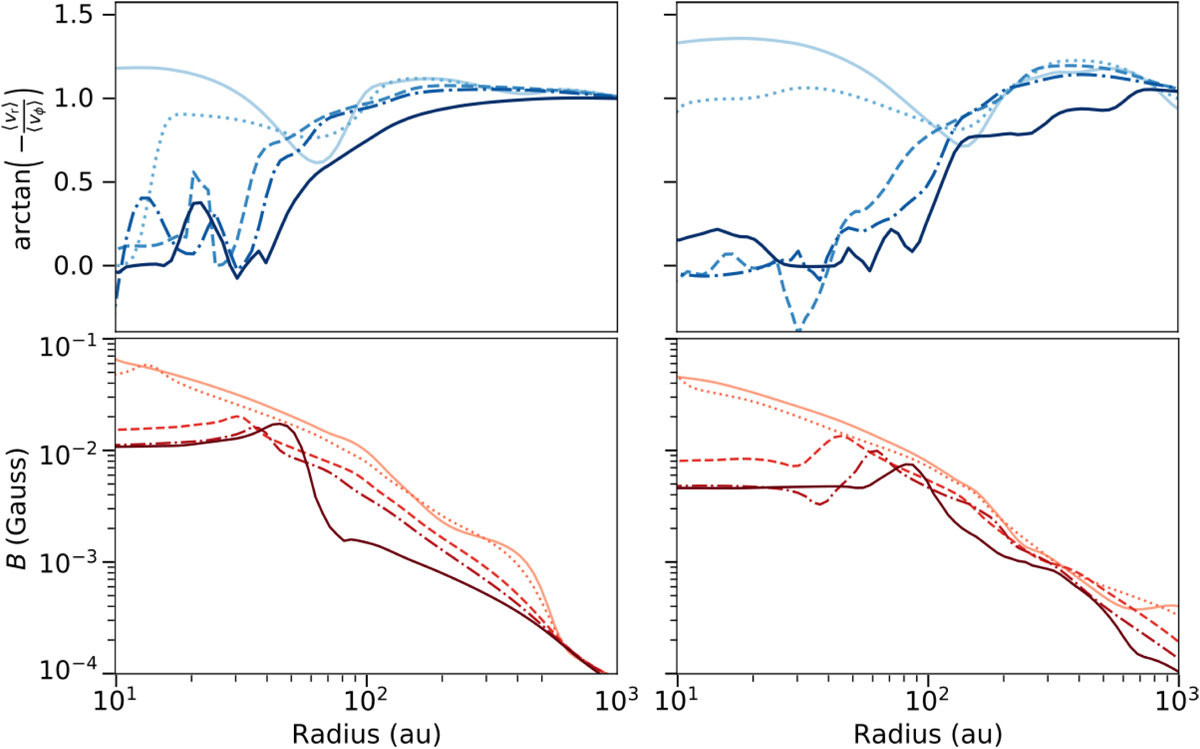
rotation

infall

from light to dark colors: high to low ionization rates

see also Wurster et al. 2018

Streamers!*

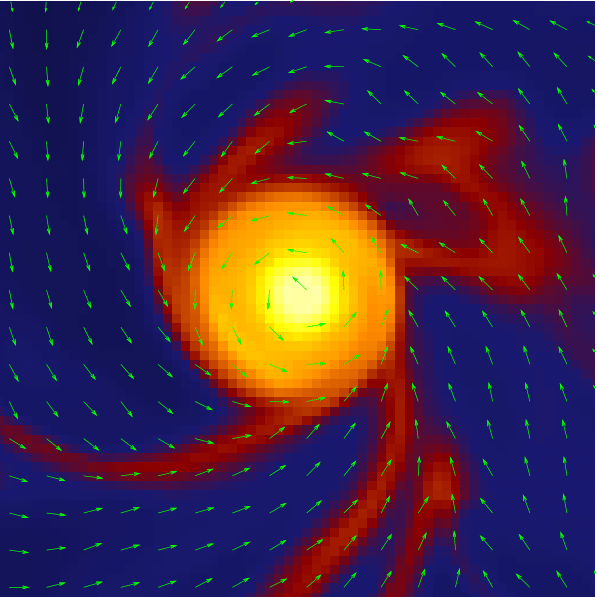
What about magnetic fields?

Help! Where is the disk?!

Ohmic, Ambipolar, Hall 

Turbulence

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

turbulence + MHD

Other effect: dust

dust growth weakens magnetic braking => larger disks

Zhao et al. 2018, Marchand et al. 2020

dust-rich disks from collapse

"ash-fall" scenario

Tsukamoto et al. 2021

 Lebreuilly et al. 2020

dust accumulates

*talk to Stefan Heigl!

Is this the full picture?

Credit: ALMA (ESO/NAOJ/NRAO)

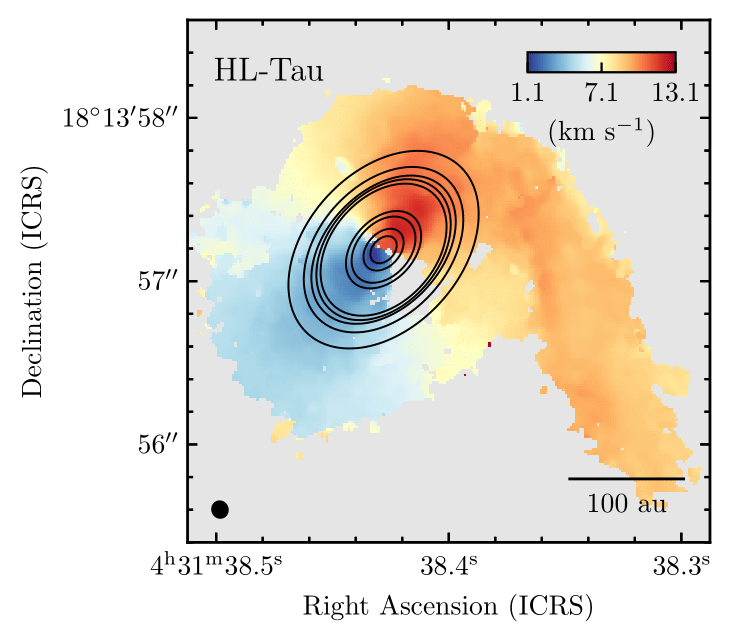
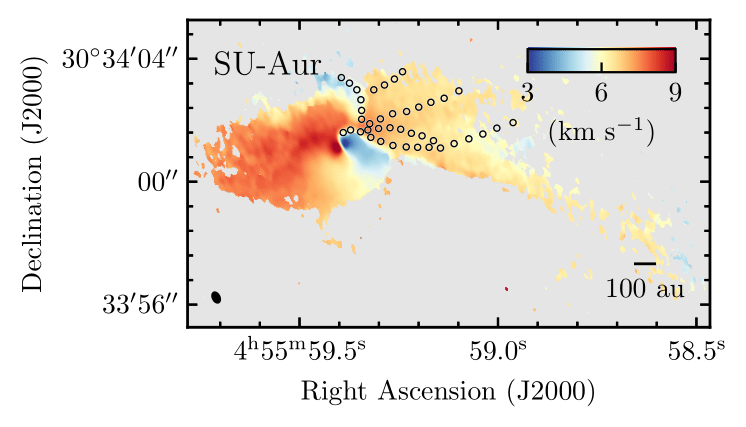
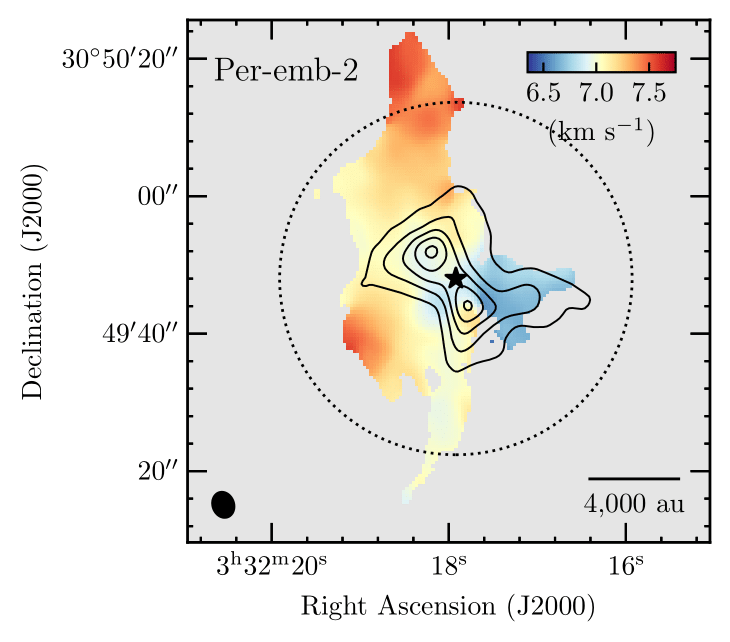
Ginski et al. 2021

Yen et al. 2019

Garufi et al. 2021

Pineda et al. 2020

50 au

BHB1 (Alves et al. 2020), GM Aur (Huang et al. 2021), IRS 63 (Segura-Cox in prep.), AB Aur (Grady et al. 1999 / Fukagawa et al. 2004), M512 Grant et al. 2021, Gupta et al. 2024, Cacciapuoti et al. 2024), ...

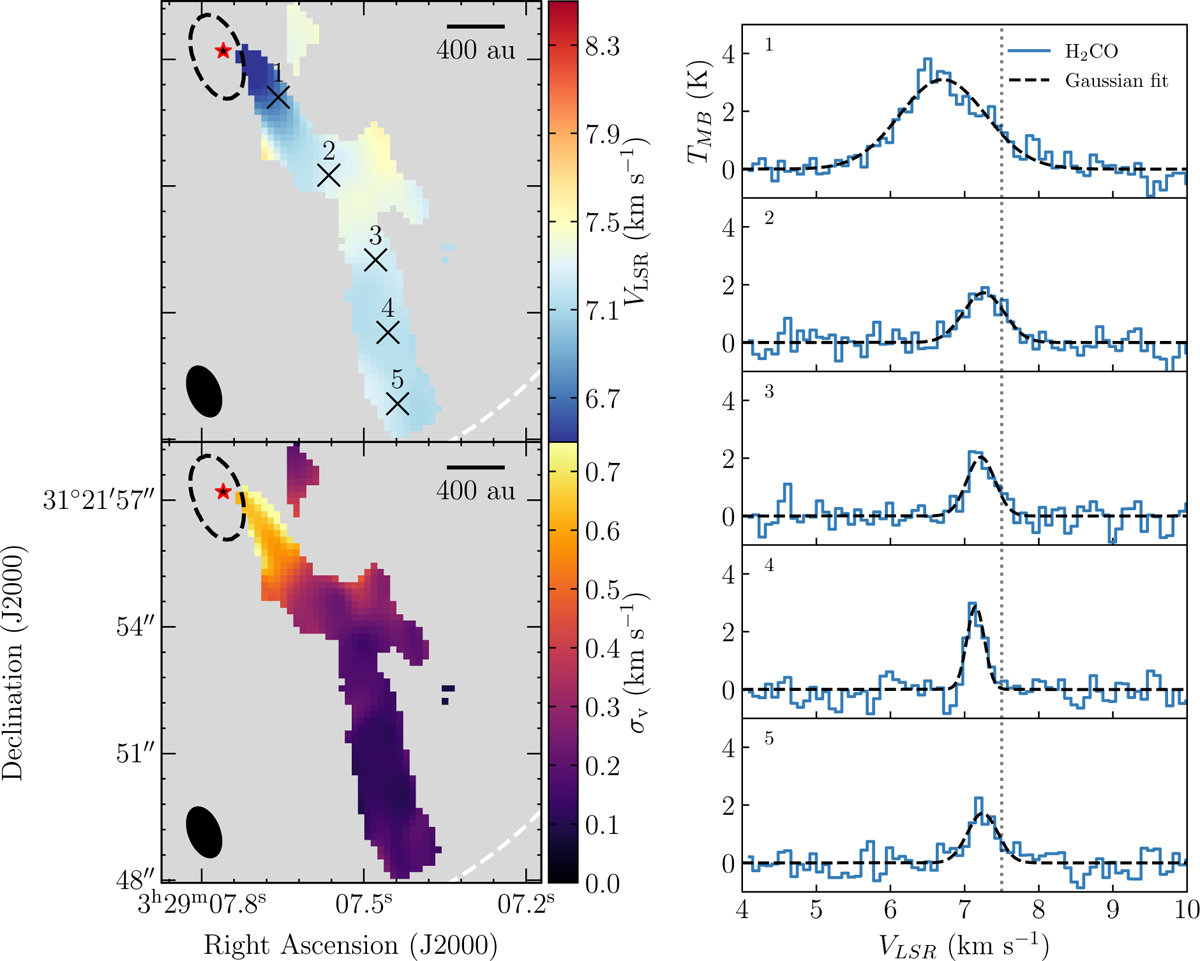
Per-emb-50

Valdivia-Mena et al. 2022

Science question:

Can we get better (statistical) constraints on the relevance and importance of (late) infall from existing simulation data? 

Streamers:

Model star formation in a Molecular Cloud

isothermal magnetohydrodynamical (MHD) with driven turbulence

adaptive mesh refinement (AMR) simulations with RAMSES

maximum resolution: ≈25 au (level of refinement: 15), root grid about ≈1600 au (level 9)

Total mass: 3000 solar masses

periodic boundary conditions

altogether 321 sink particles at last snapshot (2 Myr after the formation of the first star)

simulation setup including detailed description of sink recipe presented in Haugbølle+2018

Küffmeier, Jensen & Haugbølle '23

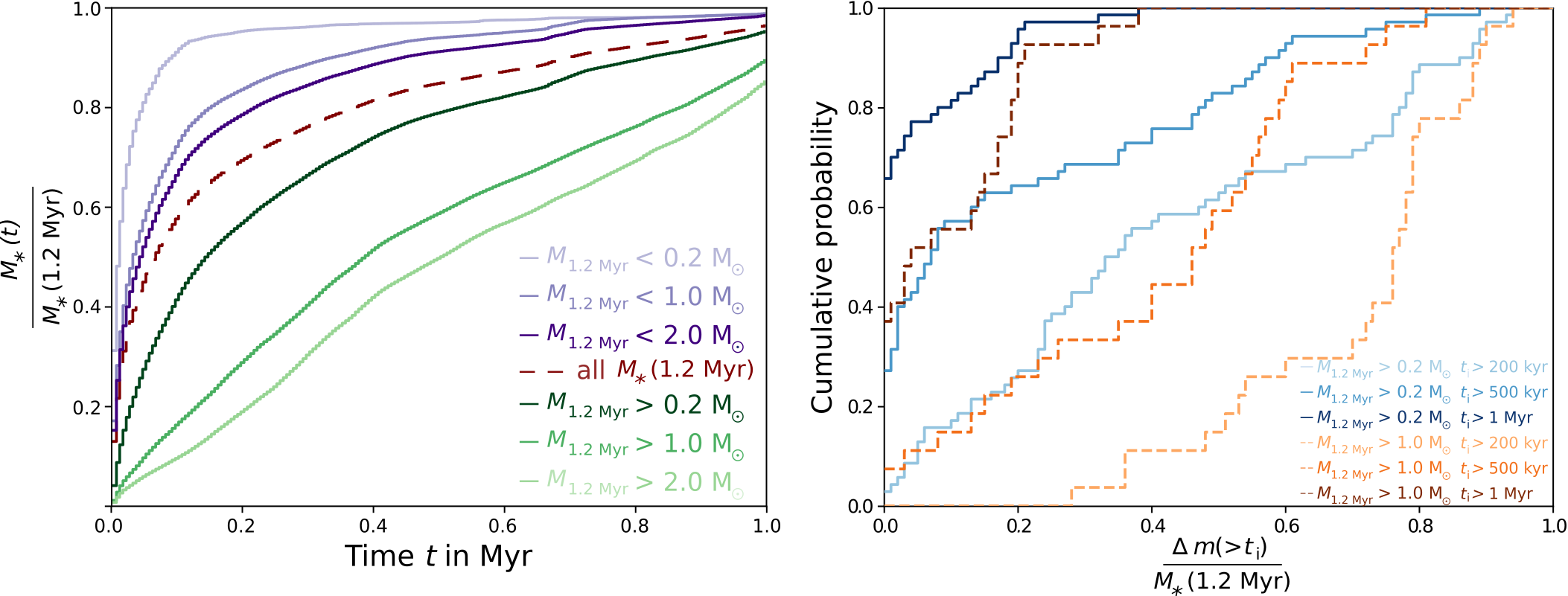
Late infall is common for stars*

 *unless they remain tiny

On average, stars with final masses of more than 1 solar mass accrete more than 50 % of their mass after 500 kyr

Note that some protostars still accrete after 1.2 Myr

Küffmeier, Jensen & Haugbølle '23

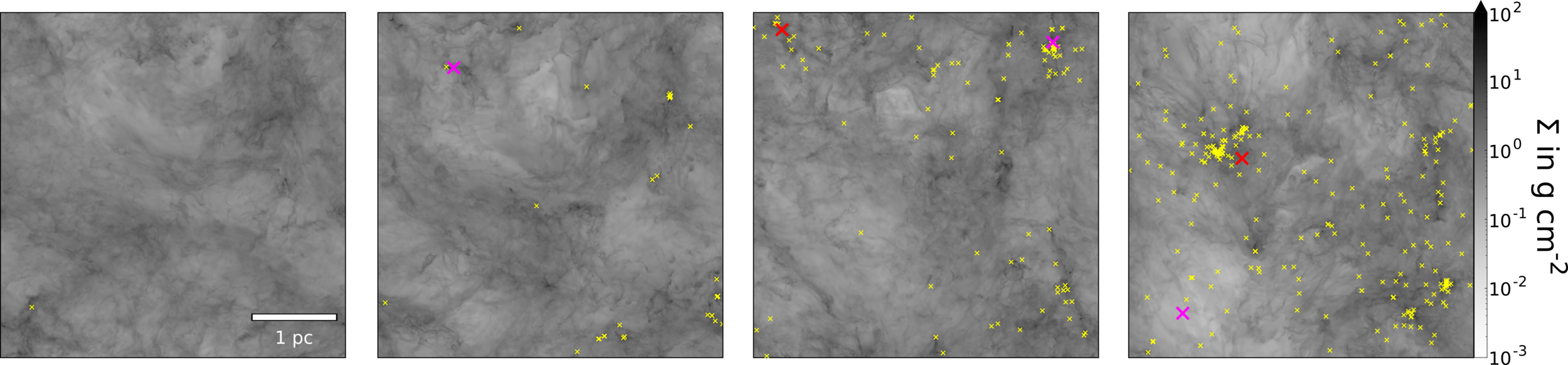
Origin of accreting gas

The accretion reservoir can extend beyond the core

(see also Smith+ 2011, Kuznetsova et al. 2020, Pelkonen+ 2021)

Two phase process:

Initial collapse followed by varying amount of post-collapse infall

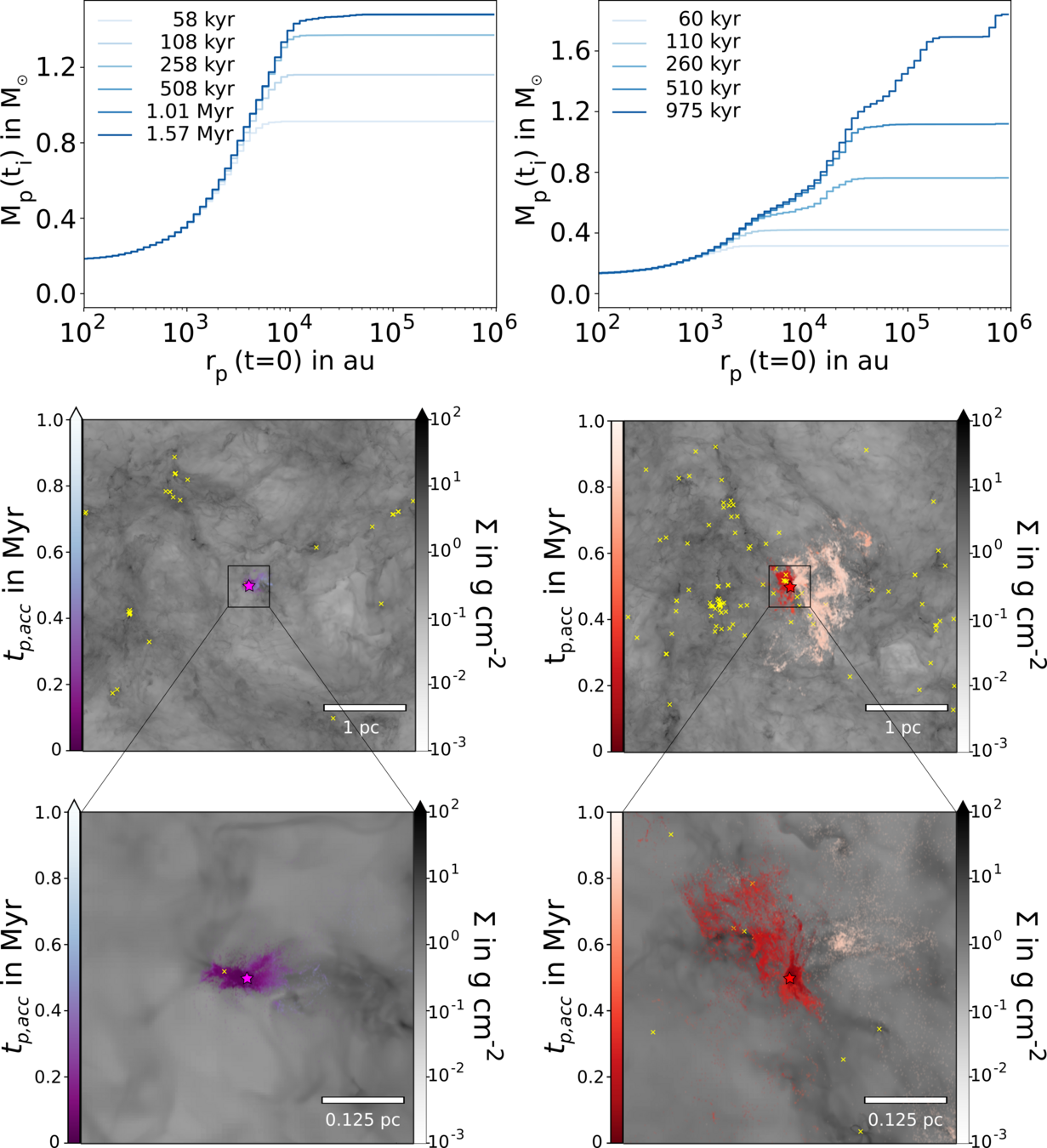
Results:

Possibility of replenishing and refreshing the mass and chemical budget

Küffmeier, Jensen & Haugbølle '23

YSOs can appear younger than they really are

How old is the protostar?

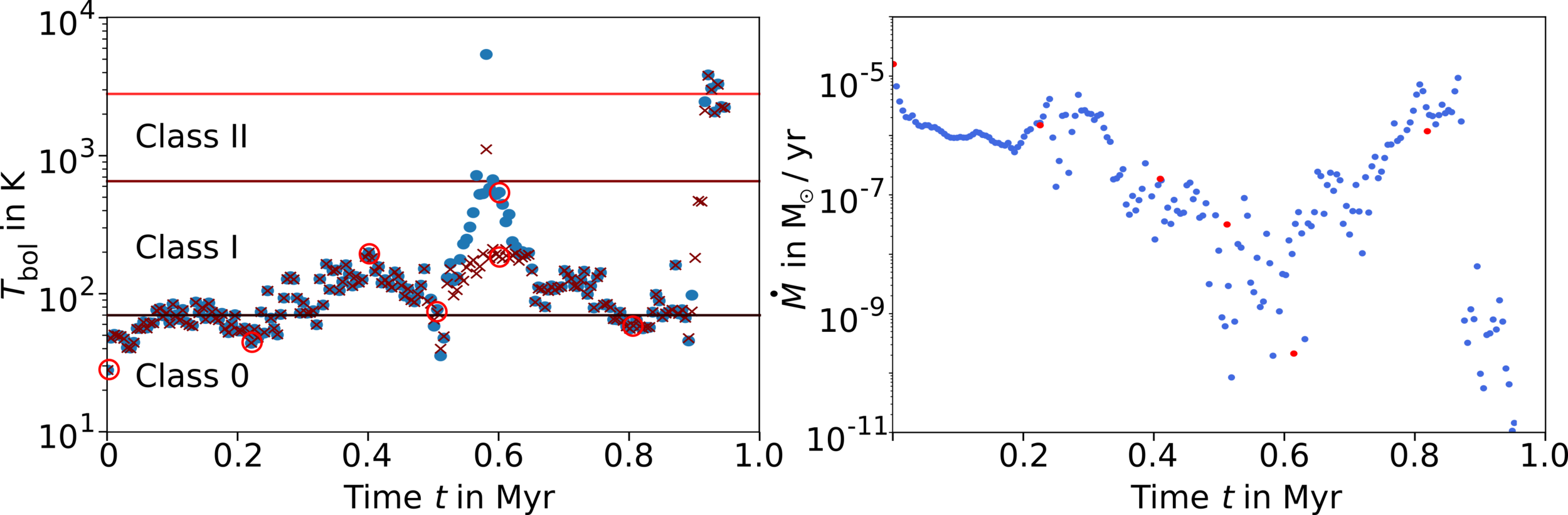
Küffmeier, Jensen & Haugbølle '23

Angular momentum budget

  • Large scatter of ang. mom.
  • Increasing specific angular momentum for increasing final stellar mass

Specific angular momentum computed from all accreting tracer particles at the first snapshot after star formation

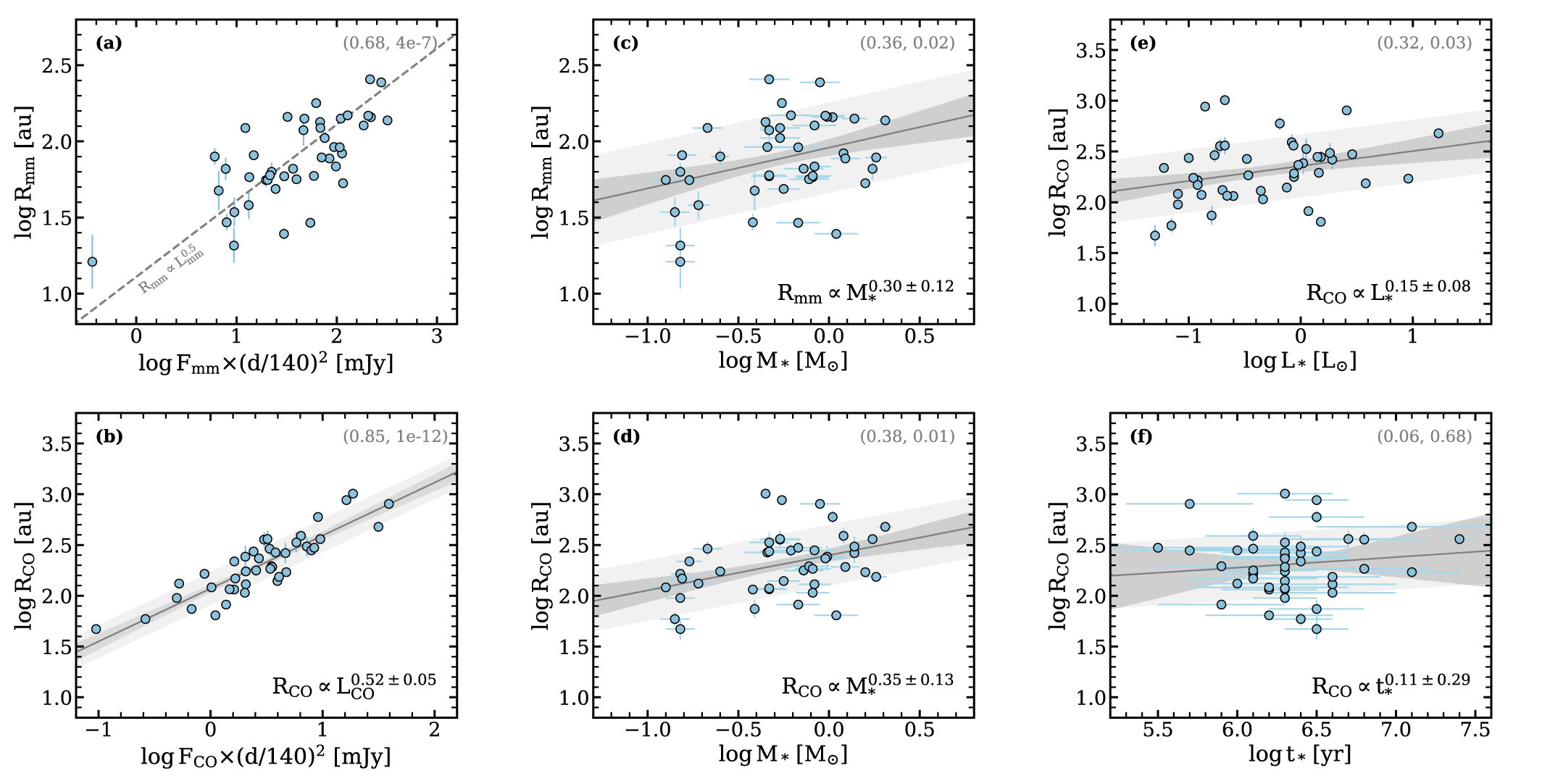
  • subtle correlation with mass (inherited by disks??)

"We find marginal relationships between disk sizes and M*." (Long+ 2022)

Küffmeier, Jensen & Haugbølle '23

On average, stars with increasing final mass undergo prolonged infall

Orientation of star-disk systems can change substantially

Küffmeier, Haugbølle, Pineda & Segura-Cox in prep

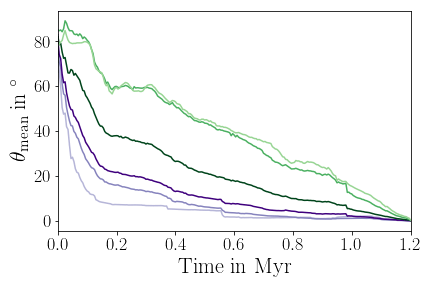
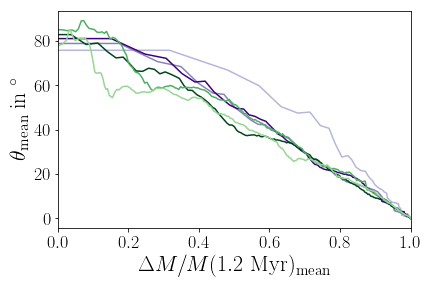
Post-collapse infall is more anisotropic than initial collapse

Orientation of infall

Streamers & shadows: signs of infall

Formation of misaligned configuration

synthetic image

Krieger, Küffmeier et al. subm.

Küffmeier, Dullemond, Reissl & Goicovic 2021

Ginski et al. 2021 (see also Labdon et al. 2023)

300 au

in agreement with Bate 2018

Credit: NASA/ESA Hubble space telescope &

ALMA (ESO/NAOJ/NRAO)

The big challenge:

link planet to star formation

50 au

Zoom-in on embedded stars

Küffmeier et al.

2019

Küffmeier et al. 2018

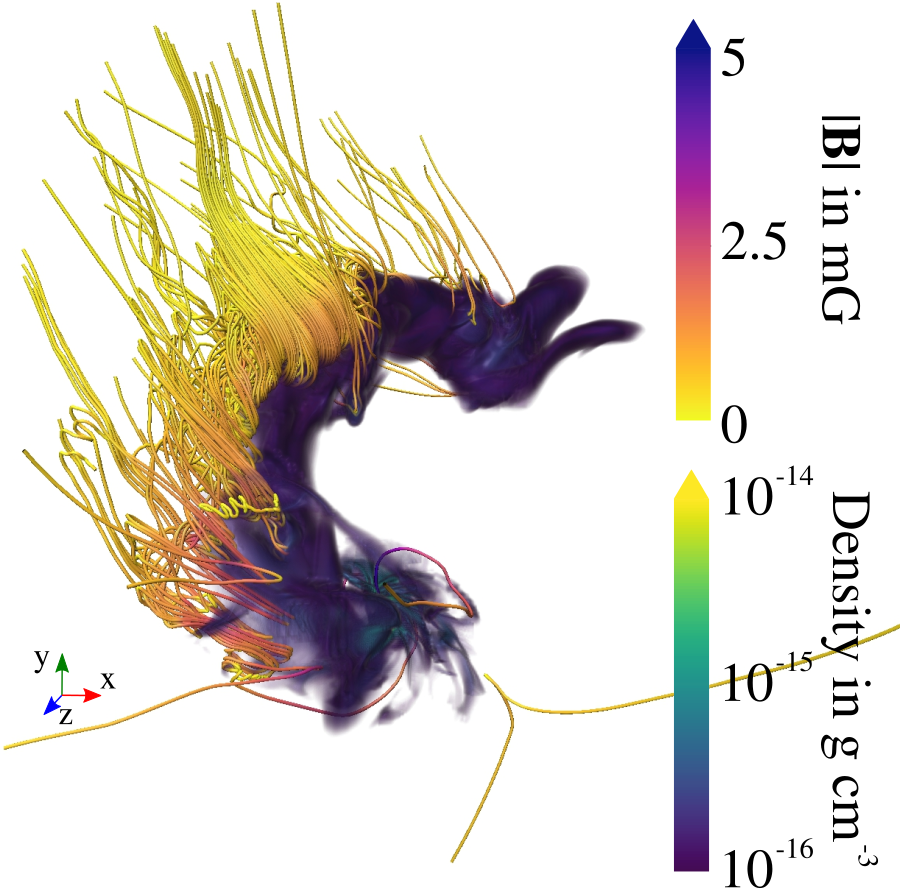
Küffmeier, Reißl et al. 2020

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

~1500 AU

Pro: self-consistent initial and boundary conditions for star formation

Con: computationally more expensive, more difficult analysis

for a similar concept, see also Lebreuilly et al. 2024

How do infall and outflow affect the disk?

Christian G. Holm

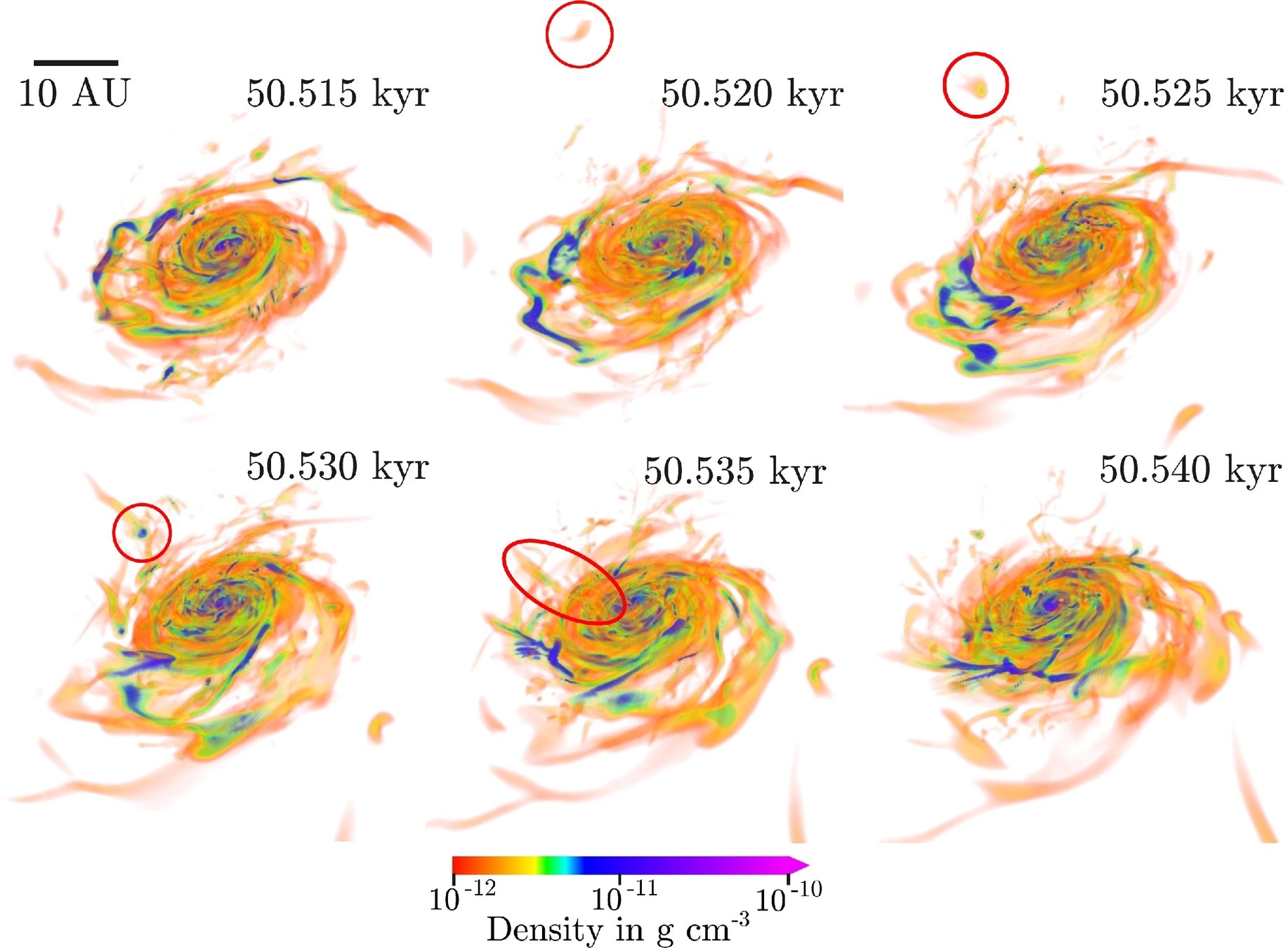
Zoom-in simulation*, 0.1 au resolution in disk, barotropic equation of state

*(run with DISPATCH: used only 1 instead of 24 nodes, yet ~10 times faster than RAMSES)

Christian G. Holm

How do infall and outflow affect the disk?

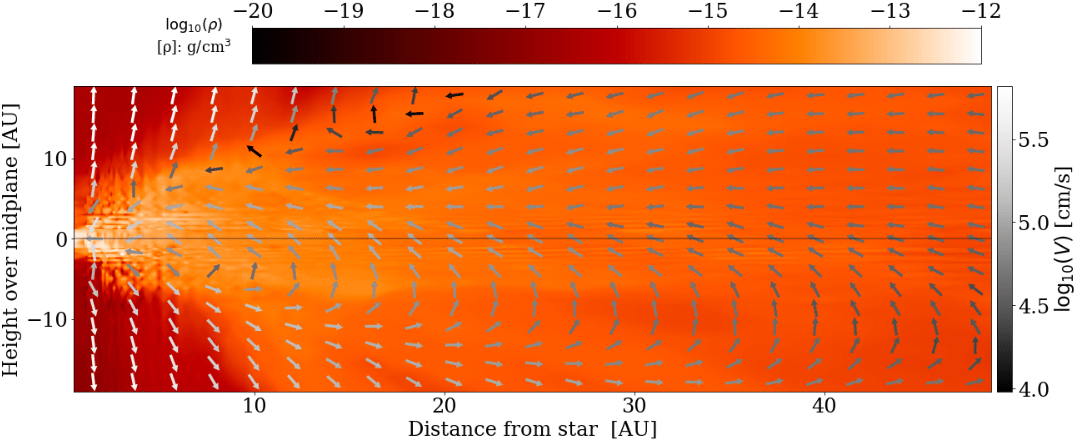
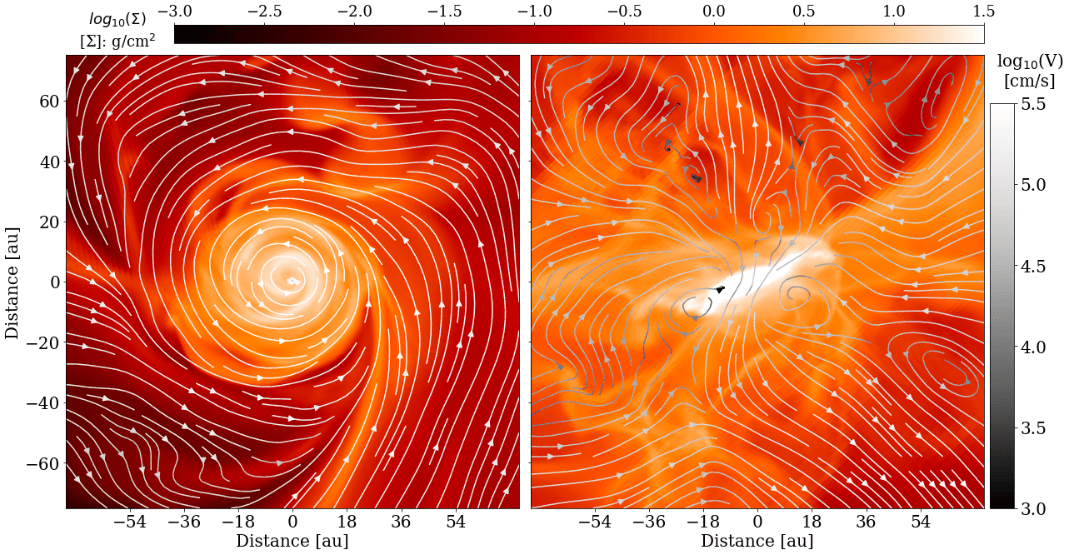
star A, t = 13 kyr

star A, t = 25 kyr

strong magnetic braking,

strong outflow

How do infall and outflow affect the disk?

Christian G. Holm

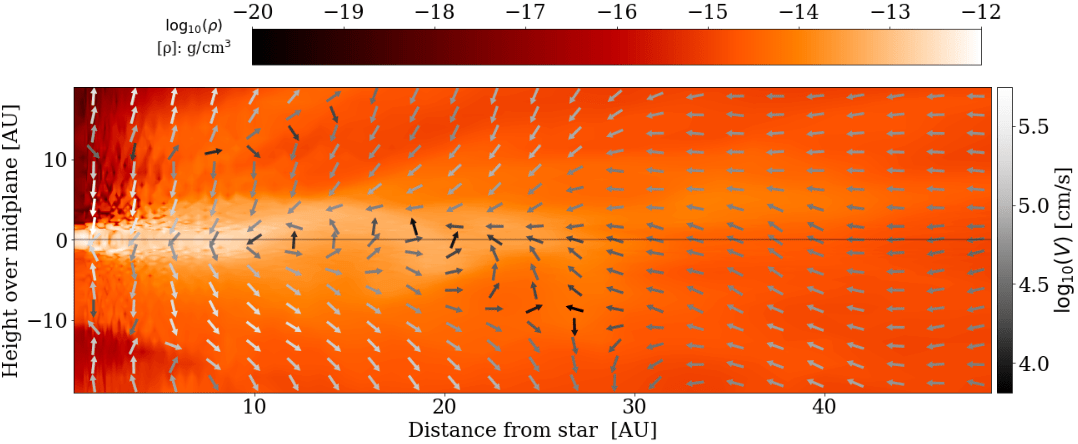
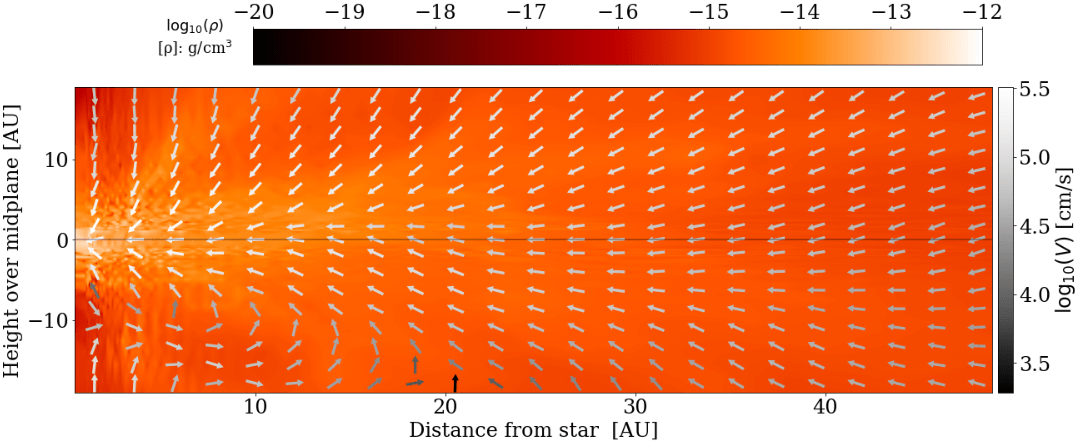
simultaneous infall and magnetically-driven outflow

star B, t = 30 kyr

  • Is the disk solely replenished with fresh material?
  • Does infall frequently lead to the formation of a new misaligned outer disk (and if yes, for how long)?
  • Is (late) infall catastrophic? Does it form a completely new one?

Key questions to be addressed in multi-scale models

  • Which percentage of ejected material returns?

(see Tsukamoto et al. 2021 ["ash-fall"], Cacciapuoti et al. 2024 ["protostellar chimney flues"])

Summary

Stars & disks are replenished and distorted by misaligned infall

YSOs can be rejuvenated

Star formation is a two-phase process consisting of mandatory initial collapse and a post-collapse infall phase (see also Smith+ '11)

Magnetic fields play an important role in:

  • regulating disk size (magnetic braking)
  • launching outflows

Lützen & Küffmeier

Christian G. Holm

How do infall and outflow affect the disk?

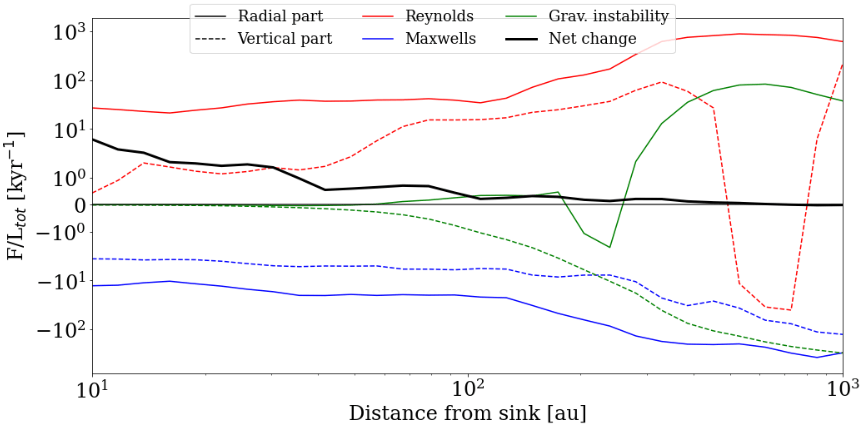
Angular momentum transport via magnetic braking

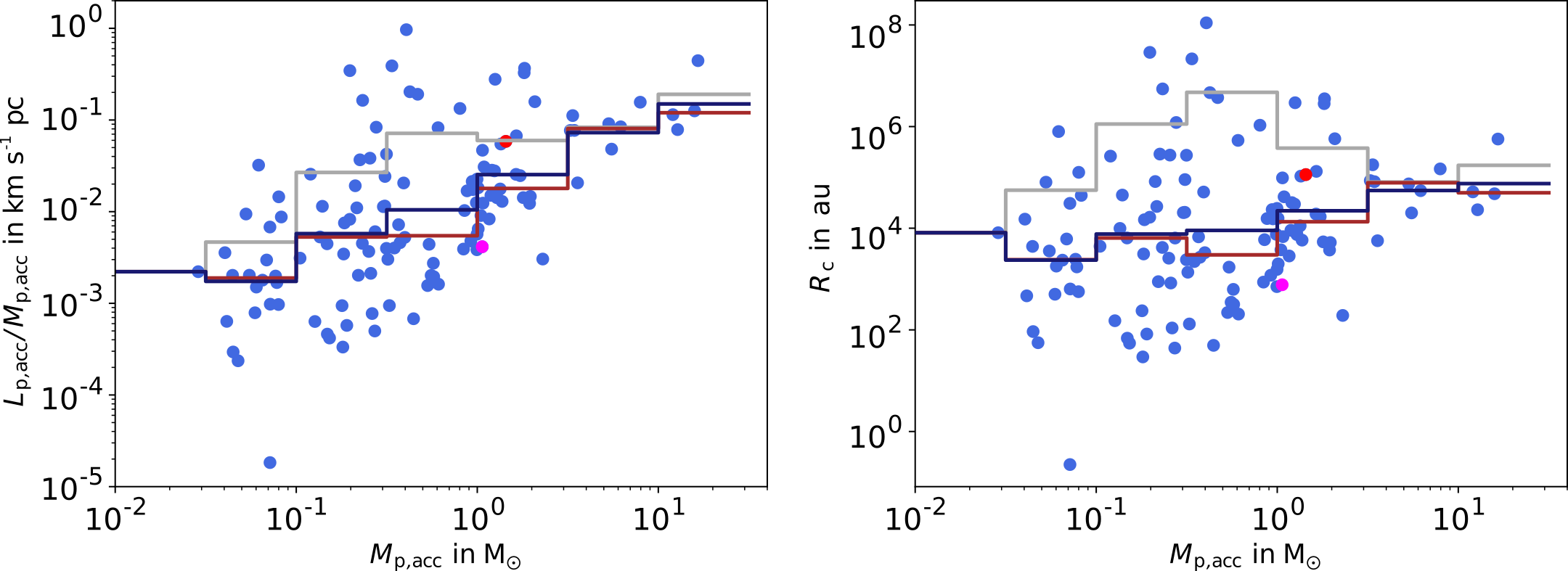
What fraction of the gas and dust returns to the disk after being ejected by an outflow?

Key question

Credit: Tsukamoto et al. 2021

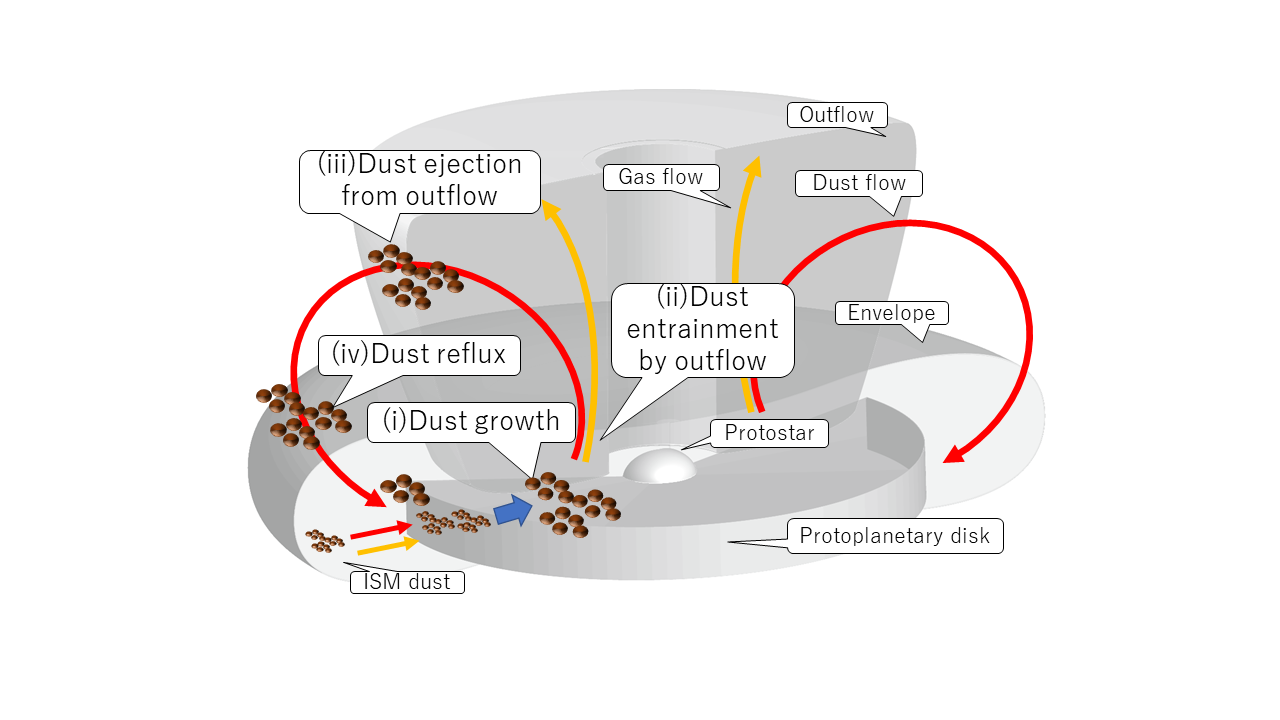
"Ash-fall" scenario aka conveyor belt

Increase in dust-to-gas ratio because dust can grow in disk and return

Tsukamoto et al. 2021

Zoom-in on embedded protostars

Küffmeier, Calcutt & Kristensen 2019

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

Küffmeier, Reißl et al. 2020

~1500 AU

Küffmeier et al. 2018

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]
\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}
\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal

Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

see also Wurster et al. 2018

Küffmeier, Zhao & Caselli 2020

Origin of accreting gas

"In the case of the more massive stars, accretion from the environment outside the original core volume is even more important than that from the core itself. [...]

The assumption of spherical symmetry cannot be applied to the majority of collapsing cores, and is never a good description of how stars accrete gas from outside the original core radius."

(Smith et al. 2011)