Molecular clouds

Stars & Planets (week 1)

Literature: Schulz, chapter 4

(see also: slides and videos by Troels Haugbølle from last year)

Michael Küffmeier

kueffmeier@nbi.ku.dk

Niels Bohr Institute

for the "real" slides, go here:

https://slides.com/kuffmeier/molecular-clouds

Recap questions

Why do the warmer phases of the interstellar medium have more blueshifted spectra compared to the colder phases?

Warmer regions have lower densities. The spectra are dominated by high-energy transitions, which causes more signal at smaller wavelengths (i.e., higher frequencies). Colder regions are denser and therefore more extinct. Light cannot easily pass through. Their spectra are dominated by lower-energy transitions, and thereby more signal at longer wavelengths.

Recap questions

Why do cooling and heating scale differently with density?

n^2\Lambda

n\Gamma

Cooling: atoms/molecules collide with electrons from the same region.

Heating: atoms/molecules are hit by external photons/atoms.

Recap questions

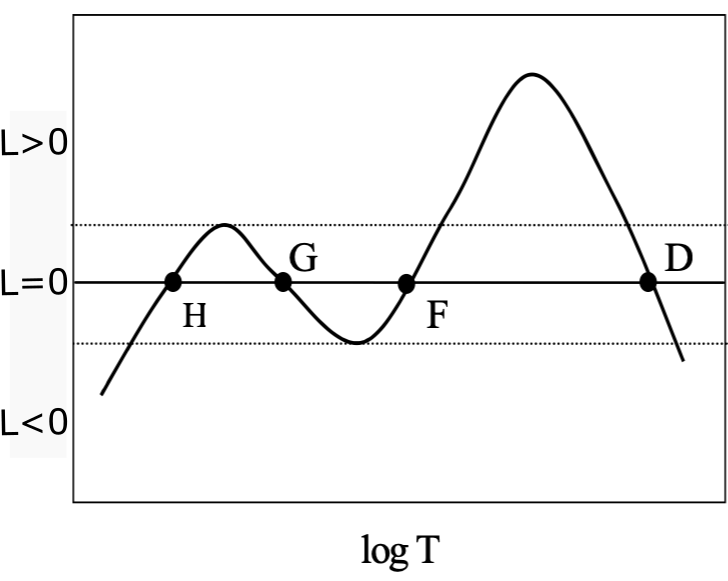
What are the stable equilibrium points and why?

cooling

L=n^2\Lambda-n\Gamma

heating

Cooling and heating have to be in balance. All marked points (H, G, F, D) fulfil that. However, only points with

\frac{\partial L}{\partial T}>0

are stable.

Consider a slight perturbation towards higher T on the curve. If we move toward higher temperatures from H, cooling dominates (L>0) and the system returns to point H.

Moving to higher temperatures from G and D, leads to more heating (L<0), and therefore runaway processes.

Molecular clouds

Molecular clouds

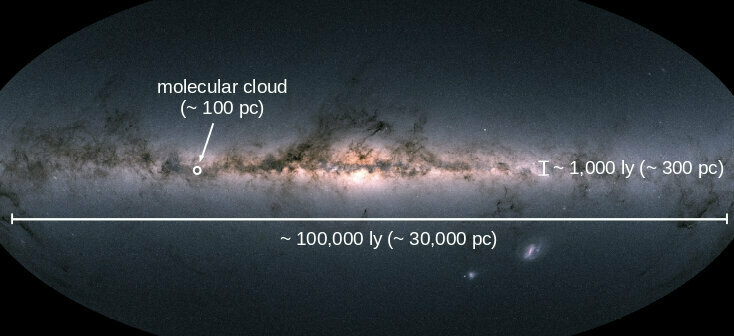
Molecular clouds only cover a tiny fraction of the volume

Molecular clouds

Molecular gas and dust

T \sim 10 \, \mathrm{K}

stars form in such molecular clouds

molecular clouds are the densest component of the ISM

Milky Way: Filling factor: <1 %, mass ~

2.5 \times 10^9 \, M_{\odot}

10^{2} \mathrm{cm}^{-3} < n < 10^{6} \mathrm{cm}^{-3}

consist of various molecules, but mostly molecular hydrogen

How do we know the mass?

Molecular clouds

Molecular gas and dust

T \sim 10 \, \mathrm{K}

Milky Way: Filling factor: <1 %, mass ~

2.5 \times 10^9 \, M_{\odot}

10^{2} \mathrm{cm}^{-3} < n < 10^{6} \mathrm{cm}^{-3}

consist of various molecules, but mostly molecular hydrogen

How do we know the mass?

Molecular hydrogen lacks dipole moment.

Its lowest energy transition occurs at > 500 K. T=10 K in molecular clouds. Too low!

Ideas?

Molecular clouds

CO is the second most abundant molecule in molecular clouds ...

... and it has dipole moments with low-energy transitions of

5 K < T < a few 100 K.

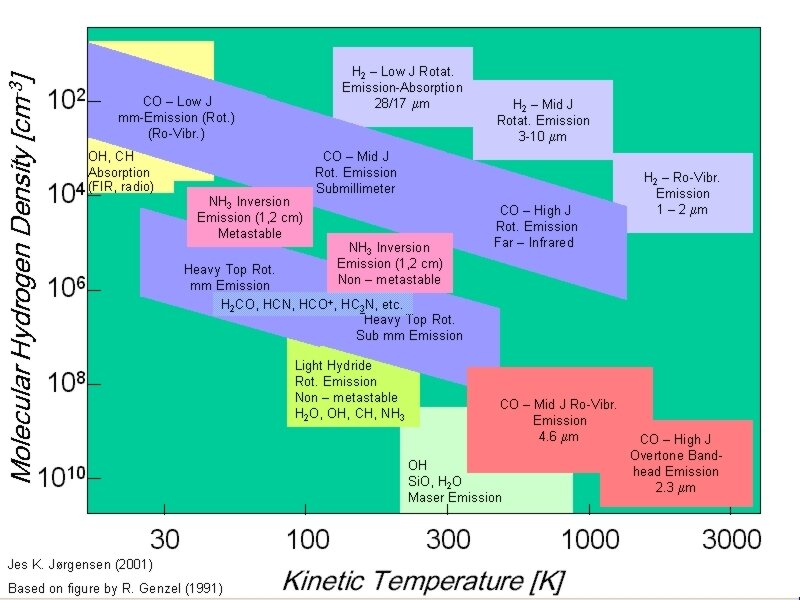
Molecular cloud survey CO J=??? (telescope: PLANCK)

Molecular gas and dust

T \sim 10 \, \mathrm{K}

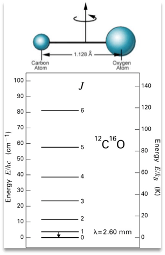
CO J=1->0: 5.5 K

CO J=2->1: 11 K

CO J=8->7: 185 K

Which transition is it?

Molecular clouds

Molecular gas and dust

T \sim 10 \, \mathrm{K}

Milky Way: Filling factor: <1 %, mass ~

2.5 \times 10^9 \, M_{\odot}

10^{2} \mathrm{cm}^{-3} < n < 10^{6} \mathrm{cm}^{-3}

consist of various molecules, but mostly molecular hydrogen

measurements of CO yield mass if CO-to-H mass-ratio is known

(see Schulz p. 53)

also possible to observe other molecules and get a more complete and comprehensive picture

Molecular clouds

Categorisation

dynamical entities and dominated by supersonic turbulence

From large to small

Molecular cores (<0.1 pc), gravitationally unstable and precursors of (proto)stars

Giant molecular clouds (~30 to 100 pc), 10 to 10 M

sun

Molecular clumps (~1 pc), ~100 M

sun

Molecular clouds (~5 to 10 pc), 10 to 10 M

sun

(diffuse clouds; only <25 % H )

Molecular clouds

Hierarchy

Larson's relations

dynamical, dominated by supersonic turbulence, and approx. isothermal at ~10 K (balance cosmic-ray heating and dust cooling)

v\approx1 \left(\frac{R}{1 \mathrm{pc}}\right)^{0.4} \mathrm{km} \, \mathrm{s}^{-1}

M\approx 230 \left(\frac{R}{1 \mathrm{pc}}\right)^{2.4} \mathrm{M}_{\odot}

n\approx 2000 \left(\frac{R}{1 \mathrm{pc}}\right)^{-1} \mathrm{cm}^{-3}

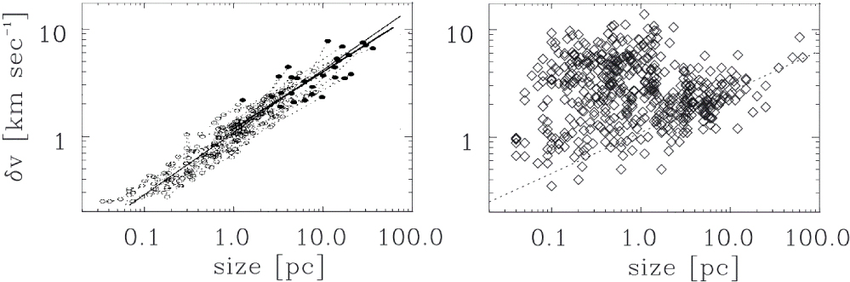
Reading recommendation! https://astrobites.org/2012/11/18/astrophysical-classics-larsons-laws/

based on data by Heyer et al. 2004

Molecular clouds

Virial theorem

\frac{1}{2} \frac{\partial^2I }{\partial t^2} = 2 \mathcal{T}+2\mathcal{U}+\mathcal{W}+\mathcal{M}

kinetic energy

moment of inertia

thermal energy

gravitational energy

magnetic energy

in principle only valid for isolated system

NO energy conservation in molecular clouds! Radiation keeps clouds at ~10 K despite plenty of shocks (conversion of kinetic to thermal energy)

...but "fresh" supply from larger scales yields statistical balance

Molecular clouds

Virial theorem

\frac{1}{2} \frac{\partial^2I }{\partial t^2} = 2 \mathcal{T}+2\mathcal{U}+\mathcal{W}+\mathcal{M}

kinetic energy

moment of inertia

thermal energy

gravitational energy

magnetic energy

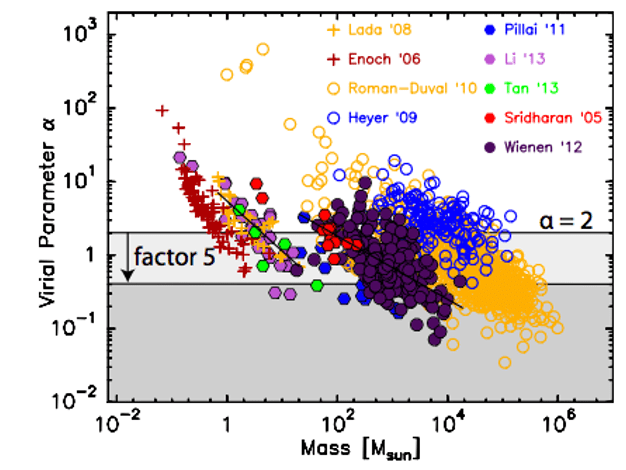
for a typical molecular cloud:

2\mathcal{T}\sim\mathcal{W}>\mathcal{M}\gg2\mathcal{U}

virial number indicates how easy a system collapses

\alpha_{\mathrm{vir}} = \frac{2\mathcal{T}}{\mathcal{W}} = \frac{2\cdot \frac{1}{2} M v^2_{\mathrm{rms}}}{\frac{3}{5}\frac{G \, M^2}{R}}=\frac{5}{3}\frac{v_{\mathrm{rms}}^2R}{GM}

Molecular clouds

Virial theorem

\alpha_{\mathrm{vir}} = \frac{2\mathcal{T}}{\mathcal{W}} =\frac{5}{3}\frac{v_{\mathrm{rms}}^2R}{GM}

What happens?

\alpha_{\rm vir} \gg 1

\alpha_{\rm vir} \ll 1

kinetic energy dominates, cloud disperses

gravitational energy dominates, cloud collapses

Molecular clouds

Virial theorem

\alpha_{\mathrm{vir}} = \frac{2\mathcal{T}}{\mathcal{W}} =\frac{5}{3}\frac{v_{\mathrm{rms}}^2R}{GM}

Molecular cloud lifetimes are determined by dynamical time

t_{\rm dyn}= \frac{R}{2}/v_{\rm rms}

computable using Larson's velocity-size relation

for

\alpha_{\mathrm{vir}} = 1

t_{\rm dyn} \approx t_{\rm ff}

gravity timescale is free-fall time

t_{\rm ff} = \left(\frac{3\pi}{32 G \rho} \right)^{0.5}

Molecular clouds

dynamical entities

Padon et al. 2017