Michael Küffmeier

C. Granzow Holm, T. Haugbølle (NBI), J. Pineda (MPE), D. Segura-Cox (Rochester), S. Reißl, C. P. Dullemond (ITA)

DSTREAM

Disk Systems That are Replenished and Evolve through Accretion of Material

Overview and history of star-disk formation

Let's go back in time to the year 2014

Wow!

Credit: ALMA (ESO/NAOJ/NRAO)

Credit:

DSHARP team

10 au

50 au

The classical picture

credit: M. Persson

star formation

planet formation

History of modeling disk formation

spherical core collapse:

rotation

magnetization (mass-to-flux ratio)

non-ideal MHD effects

dust evolution

turbulence

useful for parameter studies

\rho(r) = \frac{\rho_{\rm c} R_{\rm c}^2}{R_{\rm c}^2 + r^2}

Bonnor-Ebert sphere

or uniform density

\rho(r) = \rho_{0}

History of modeling disk formation

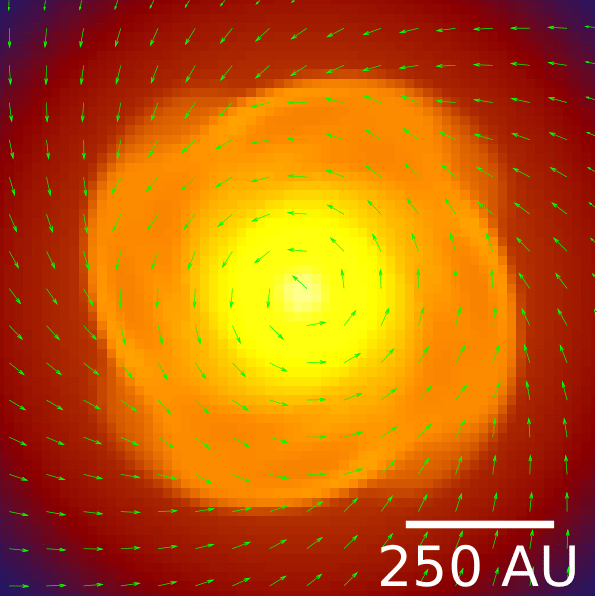
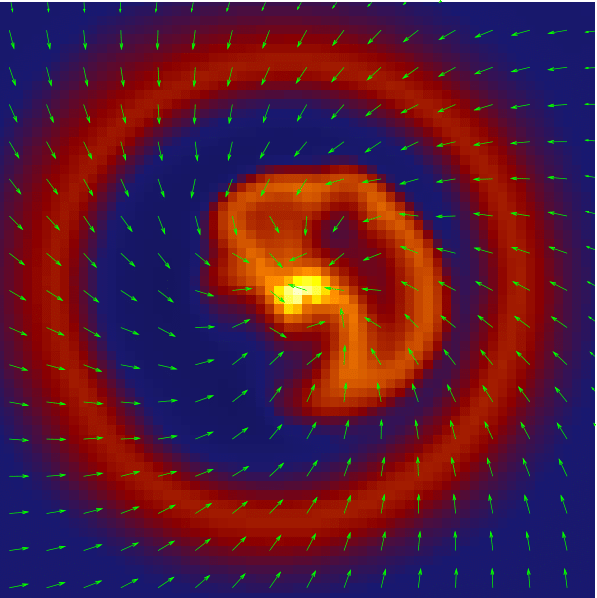
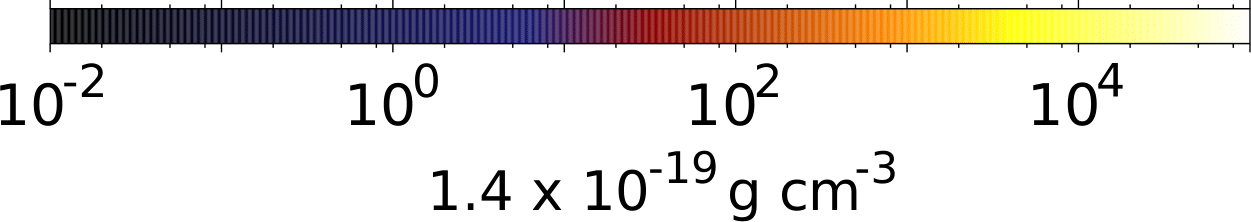
What about magnetic fields?

Help! Where is the disk?!

Santos-Lima et al. 2012

Hydro

ideal MHD

L_{\rm mag} = \int_{t_{\rm c}}^{t}\int^V r (\mathbf{J} \times \mathbf{B})_\phi \mathrm{d}V\mathrm{d}t

Magnetic braking catastrophe

Angular momentum is transported too efficiently away from the disk

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]

\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal

Non-ideal MHD

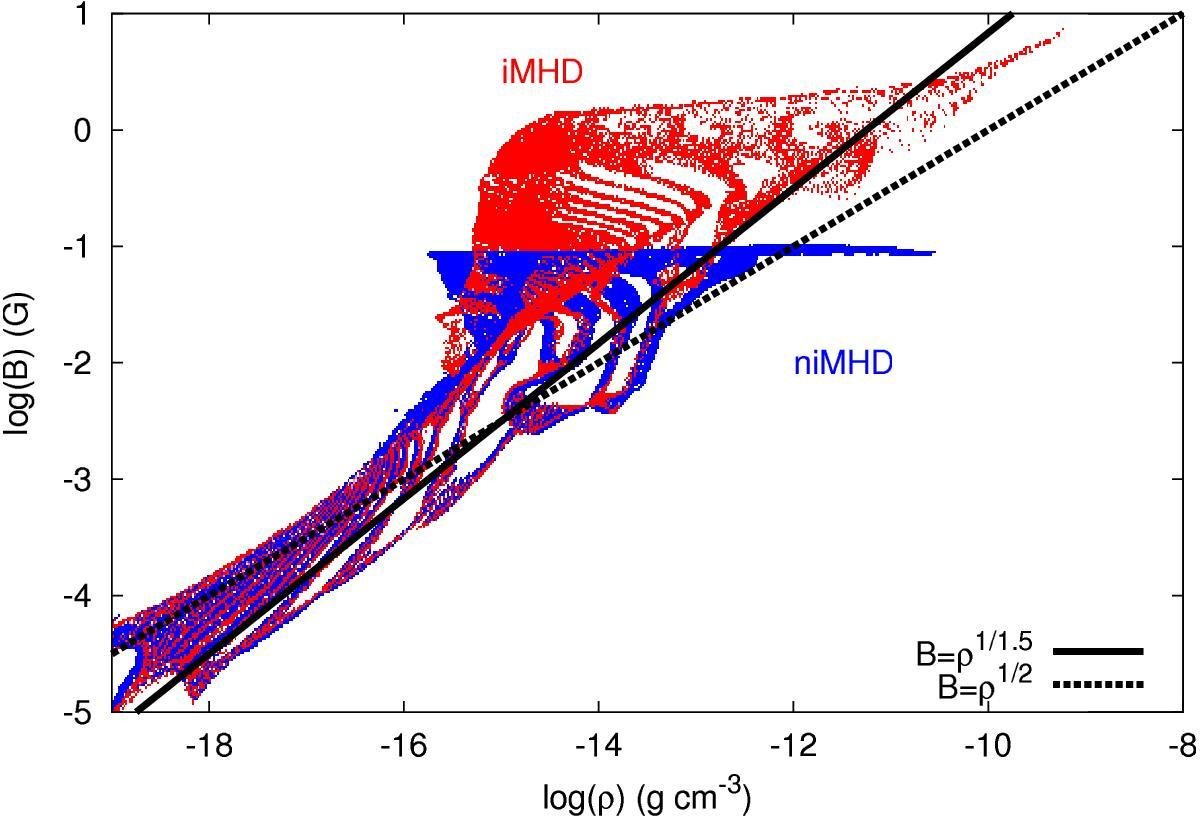
Masson et al. 2016

resistivities quench pile-up of magnetic field

avoids magnetic braking catastrophe

see Hennebelle et al. 2016 or Lee et al. 2021 for analytical studies

more references in reviews by Wurster & Li 2018 and Tsukamoto et al. 2023

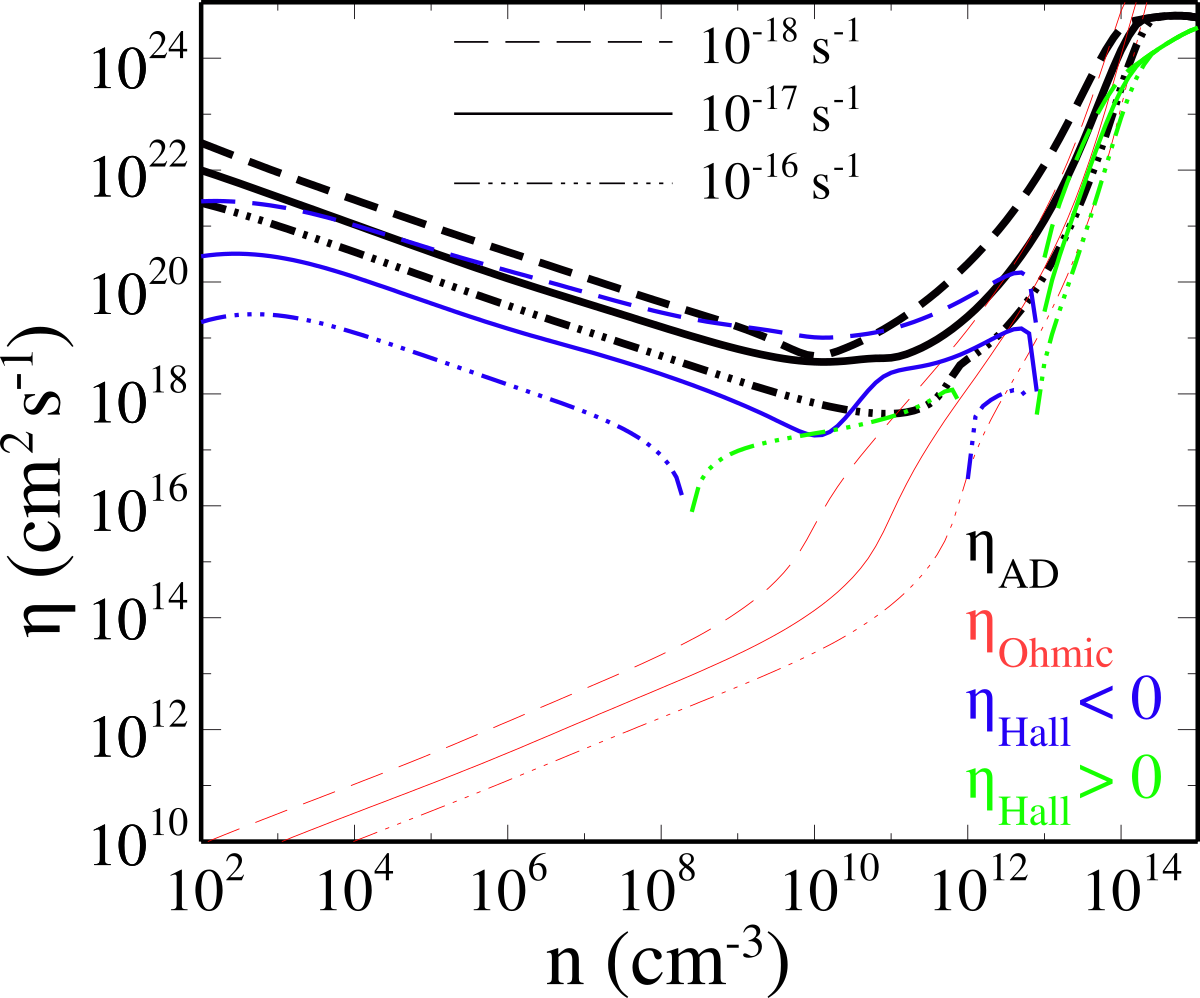
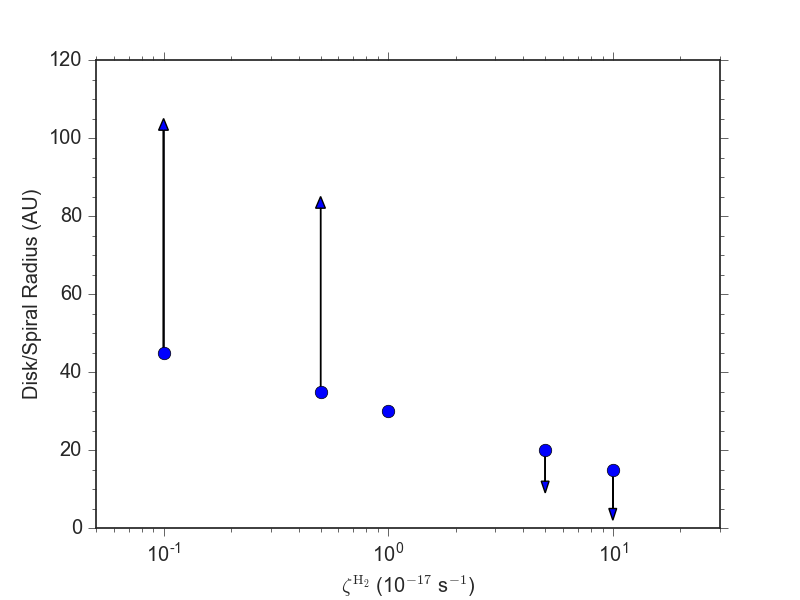
Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

Küffmeier, Zhao & Caselli 2020

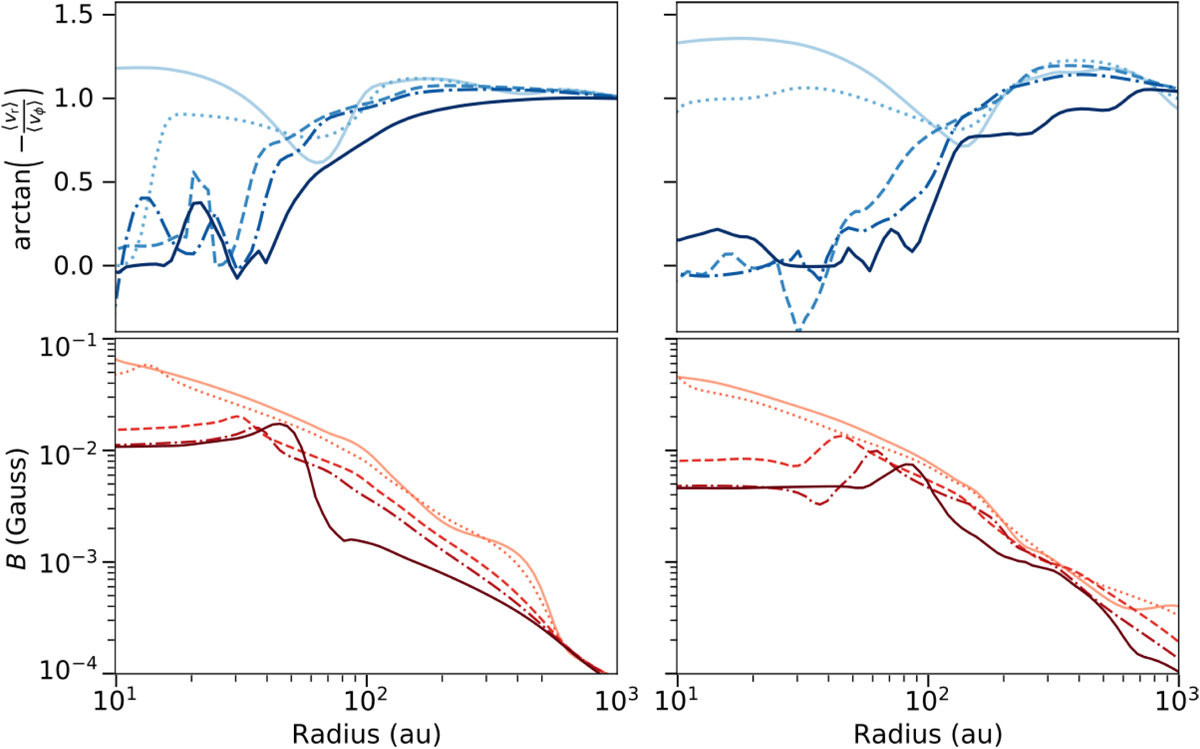
rotation

infall

from light to dark colors: high to low ionization rates

see also Wurster et al. 2018

History of modeling disk formation

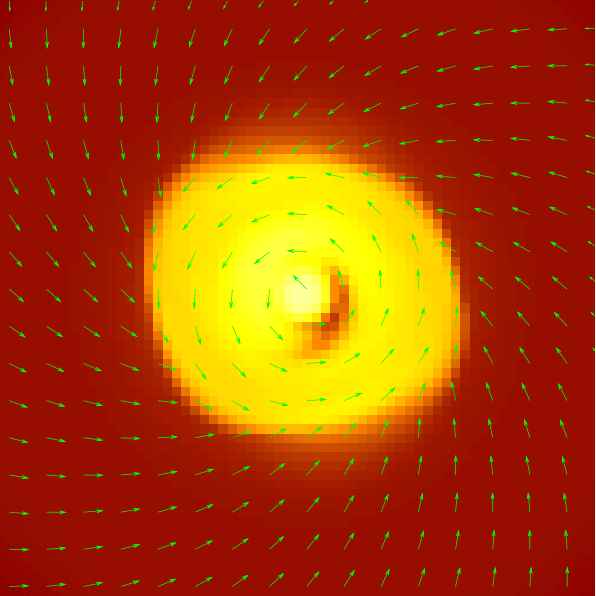
What about magnetic fields?

Help! Where is the disk?!

Ohmic, Ambipolar, Hall

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

non-ideal MHD is not a single parameter that is turned on or off!

It depends on ionization fraction.

Achtung!

see Wurster et al. 2018, Kuffmeier et al. 2020; reviews by Tsukamoto et al. 2023, Kuffmeier submitted

History of modeling disk formation

What about magnetic fields?

Help! Where is the disk?!

Santos-Lima et al. 2012

Hydro

ideal MHD

L_{\rm mag} = \int_{t_{\rm c}}^{t}\int^V r (\mathbf{J} \times \mathbf{B})_\phi \mathrm{d}V\mathrm{d}t

Magnetic braking catastrophe

Angular momentum is transported too efficiently away from the disk

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]

\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal

Non-ideal MHD

Masson et al. 2016

resistivities quench pile-up of magnetic field

avoids magnetic braking catastrophe

see Hennebelle et al. 2016 or Lee et al. 2021 for analytical studies

more references in reviews by Wurster & Li 2018, Tsukamoto et al. 2023 and Küffmeier 2024

History of modeling disk formation

Help! Where is the disk?!

Ohmic, Ambipolar, Hall

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

non-ideal MHD is not a single parameter

Caveat!

What about magnetic fields?

depends on cosmic-ray ionization rate!

for pioneering work see Galli & Shu 1993 a/b

Effect of ionization on disk size

Küffmeier, Zhao & Caselli 2020; see also Wurster et al. 2018

increasing ionization rate

enhanced magnetic braking

smaller disks

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

Maps of CR-ionization rates (e.g., NGC 1333 Pineda et al. 2024, or AG 351 & AG 354 Sabatini et al. 2023)

Küffmeier, Zhao & Caselli 2020; see also Kobayashi et al. 2023

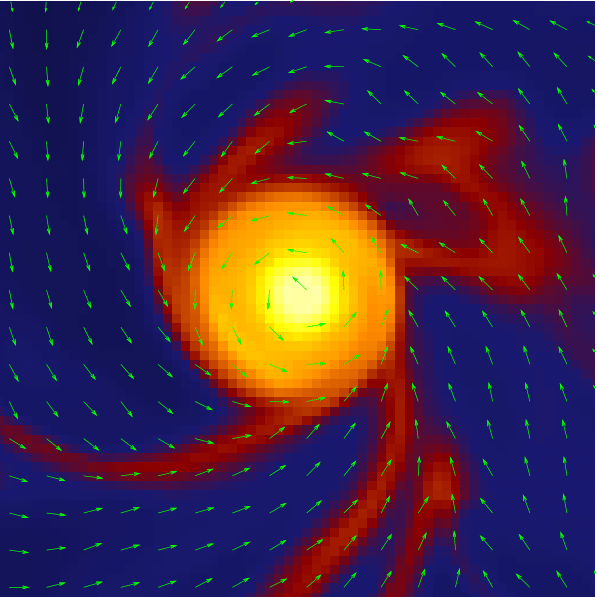
What about magnetic fields?

Help! Where is the disk?!

Ohmic, Ambipolar, Hall

Turbulence

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

turbulence + MHD

History of modeling disk formation

for more references, see reviews

(e.g., Wurster & Li 2018, Zhao et al. 2022, Tsukamoto et al. 2023, Küffmeier 2024)

see Seifried et al. 2012/13!

What about magnetic fields?

Help! Where is the disk?!

Ohmic, Ambipolar, Hall

Turbulence

Santos-Lima et al. 2012

Hydro

ideal MHD

non-ideal MHD

turbulence + MHD

Other effect: dust

dust growth weakens magnetic braking => larger disks

Zhao et al. 2018, Marchand et al. 2020

dust-rich disks from collapse

"ash-fall" scenario

Tsukamoto et al. 2021

Lebreuilly et al. 2020

dust accumulates

History of modeling disk formation

Revisiting star-disk formation from a Giant Molecular Cloud perspective

Is this the full picture?

Credit: ALMA (ESO/NAOJ/NRAO)

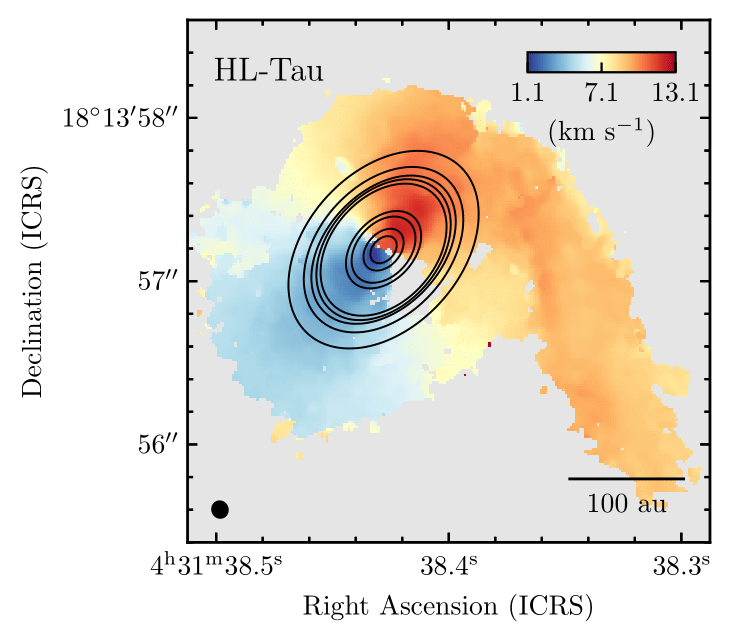
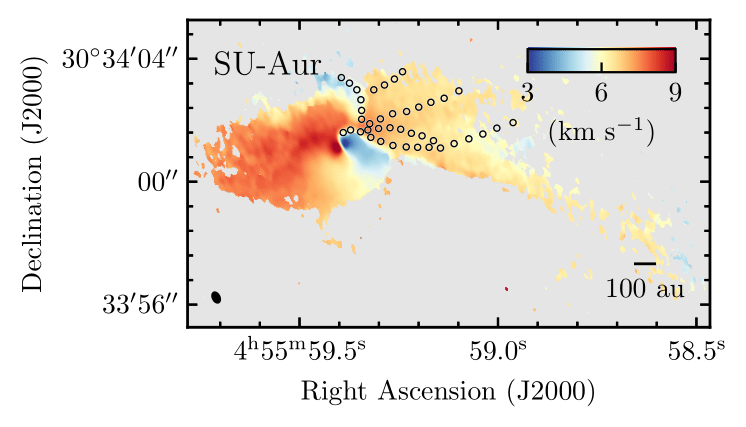
Ginski et al. 2021

Yen et al. 2019

Garufi et al. 2021

Pineda et al. 2020

50 au

BHB1 (Alves et al. 2020), GM Aur (Huang et al. 2021), IRS 63 (Segura-Cox in prep.), AB Aur (Grady et al. 1999 / Fukagawa et al. 2004), M512 Grant et al. 2021, Gupta et al. 2024, Cacciapuoti et al. 2024) ...

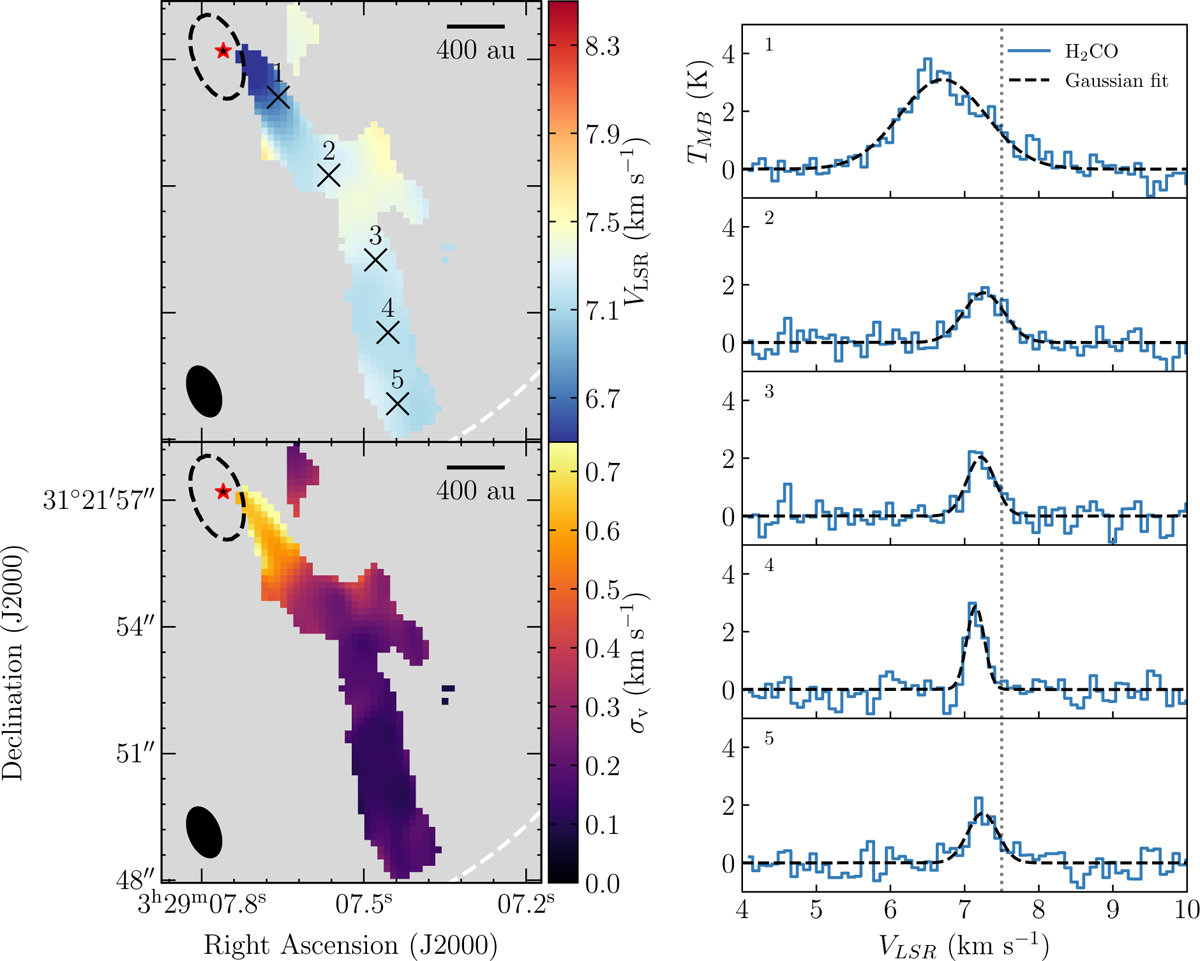
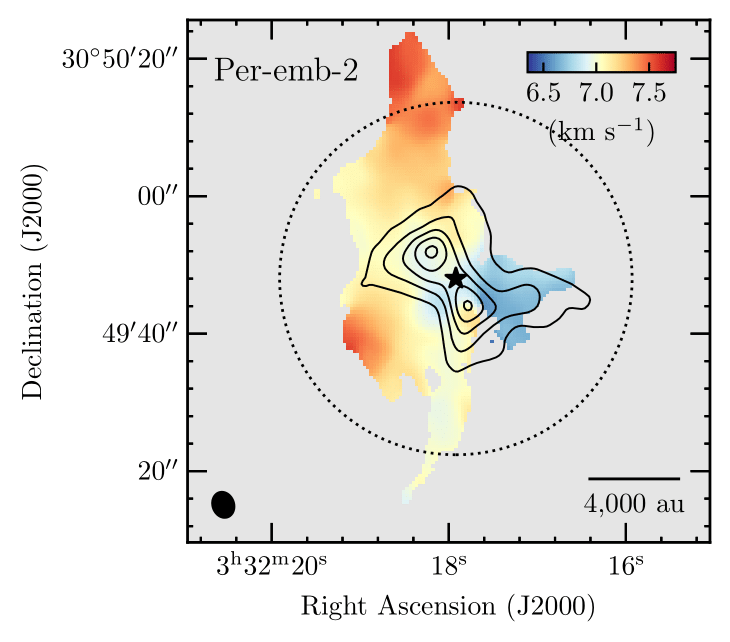
Per-emb-50

Valdivia-Mena et al. 2022

Science question:

Can we get better (statistical) constraints on the relevance and importance of (late) infall from existing simulation data?

Streamers:

Model star formation in a Molecular Cloud

isothermal magnetohydrodynamical (MHD) with driven turbulence

adaptive mesh refinement (AMR) simulations with RAMSES

maximum resolution: ≈25 au (level of refinement: 15), root grid about ≈1600 au (level 9)

3000 solar masses; periodic boundary conditions; 321 sinks forming within 2 Myr

simulation setup including detailed description of sink recipe presented in Haugbølle+2018

image based on Küffmeier, Jensen & Haugbølle '23

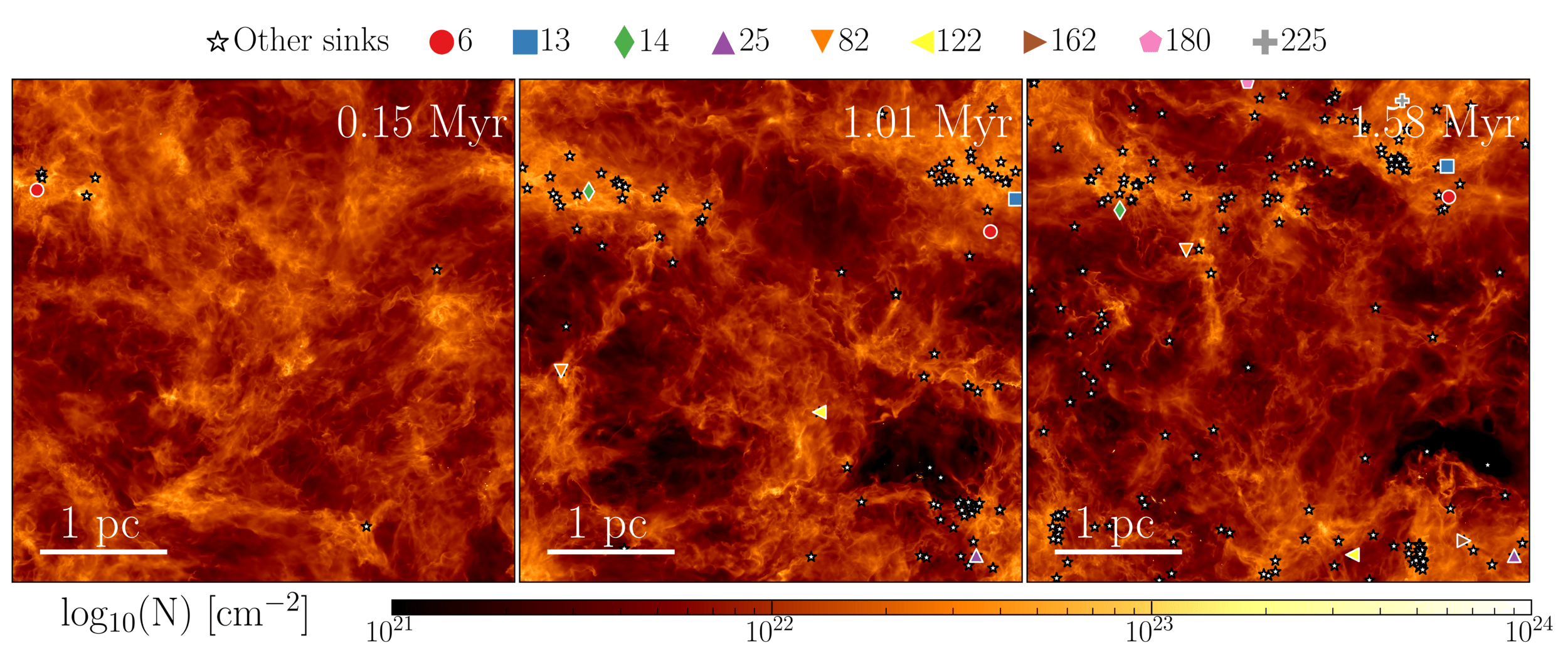
Late infall is common for stars

On average, even solar mass stars gain ~50 % of their final mass through accretion of initially unbound material

Note that some protostars still accrete after 1.2 Myr

Küffmeier, Jensen & Haugbølle '23

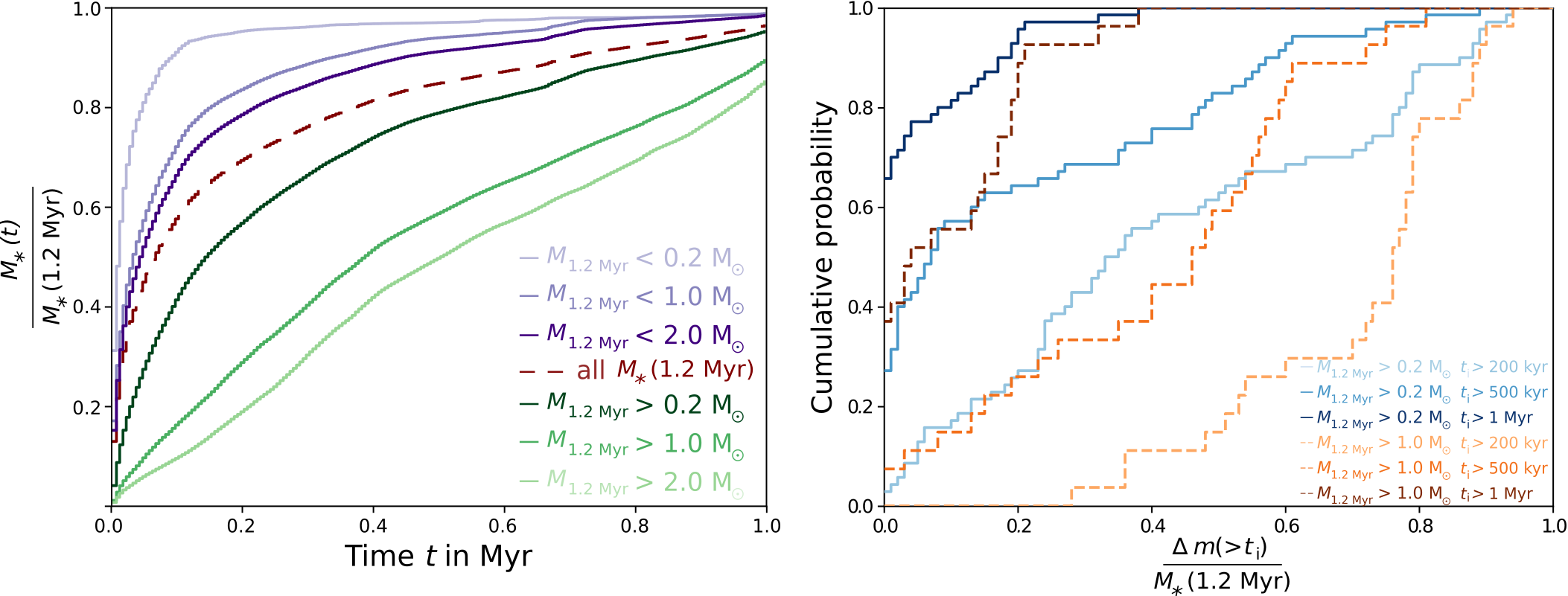
(Pelkonen et al. 2021)

Origin of accreting gas

Two phase process:

Initial collapse followed by varying amount of post-collapse infall

(see also Pelkonen+ 2021)

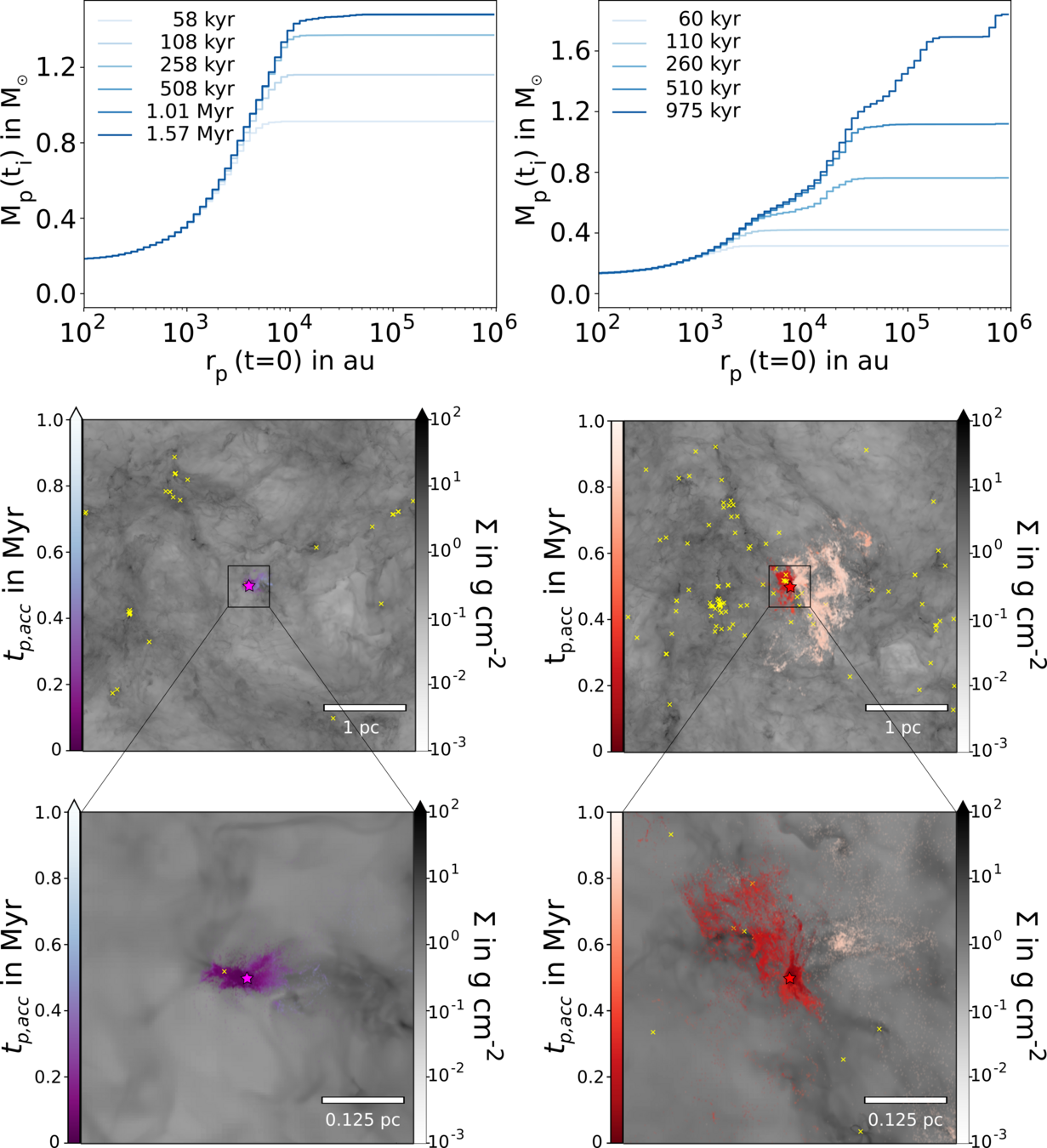
Küffmeier, Jensen & Haugbølle '23

Origin of accreting gas

"In the case of the more massive stars, accretion from the environment outside the original core volume is even more important than that from the core itself. [...]

The assumption of spherical symmetry cannot be applied to the majority of collapsing cores, and is never a good description of how stars accrete gas from outside the original core radius."

(Smith, Glover, Bonnell, Clark & Klessen 2011)

Implications of (late) infall

YSOs can appear younger than they really are

How old is the protostar?

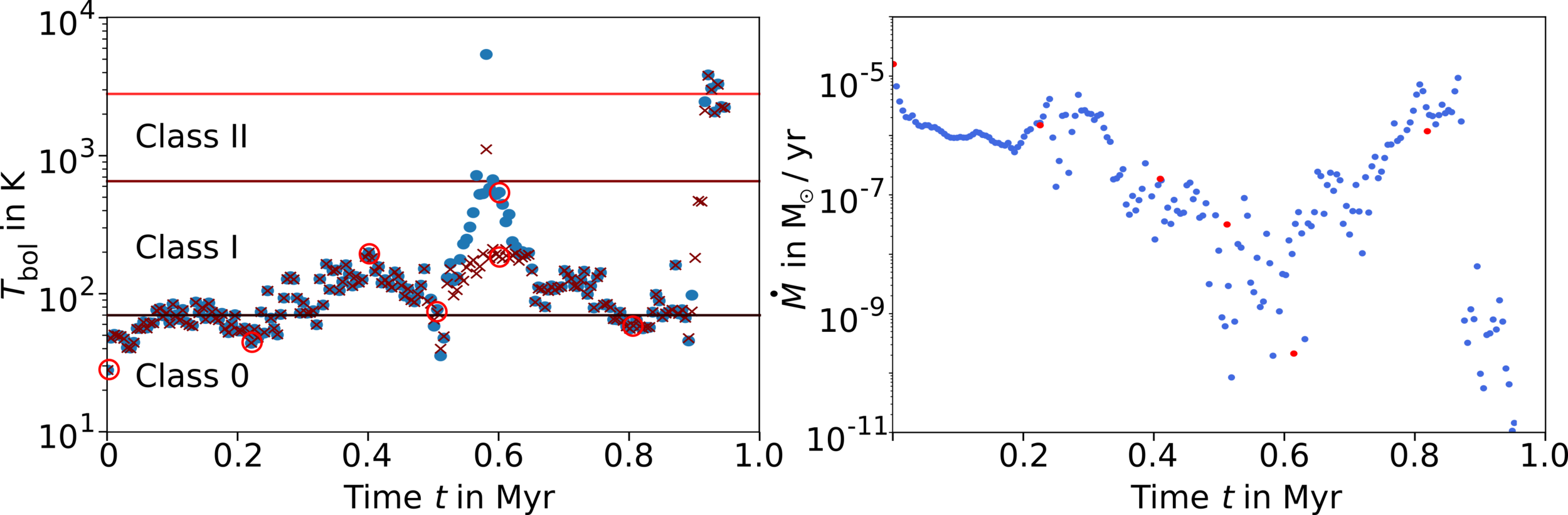
Küffmeier, Jensen & Haugbølle '23

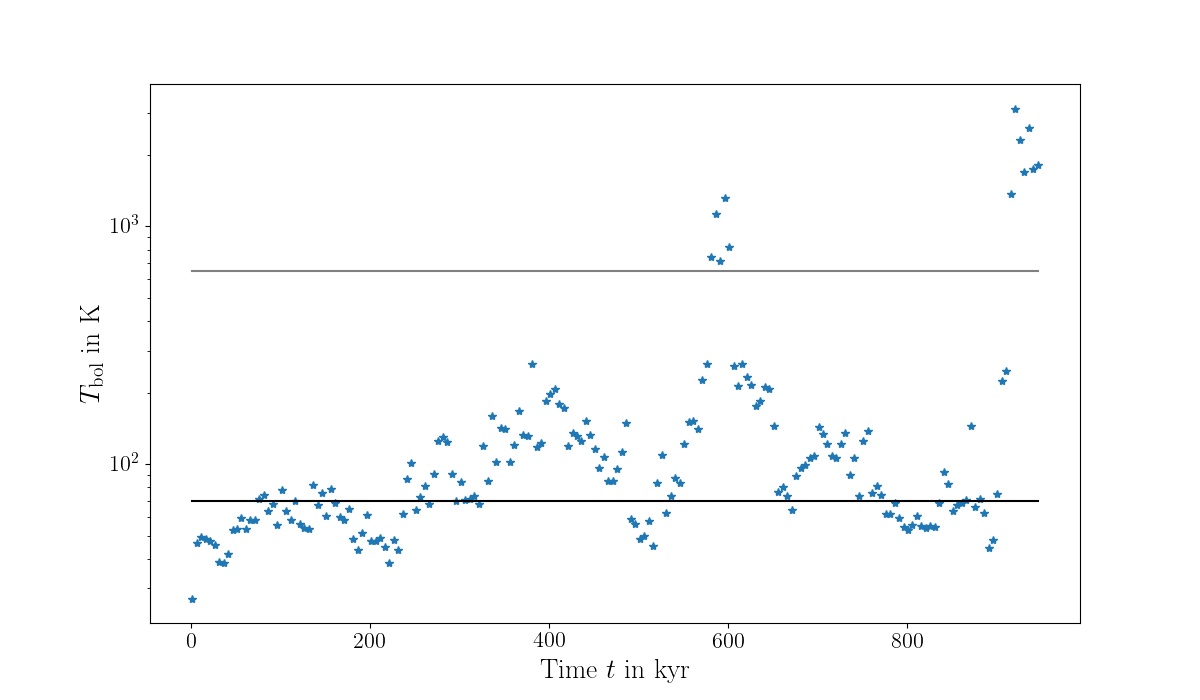
Class I

Class 0

Class II

Spreading vs wind-driven?

Manara et al. 2023

Caveat!

Infall matters. Disks can easily be wind-driven and yet grow in size through infall of gas with high angular momentum.

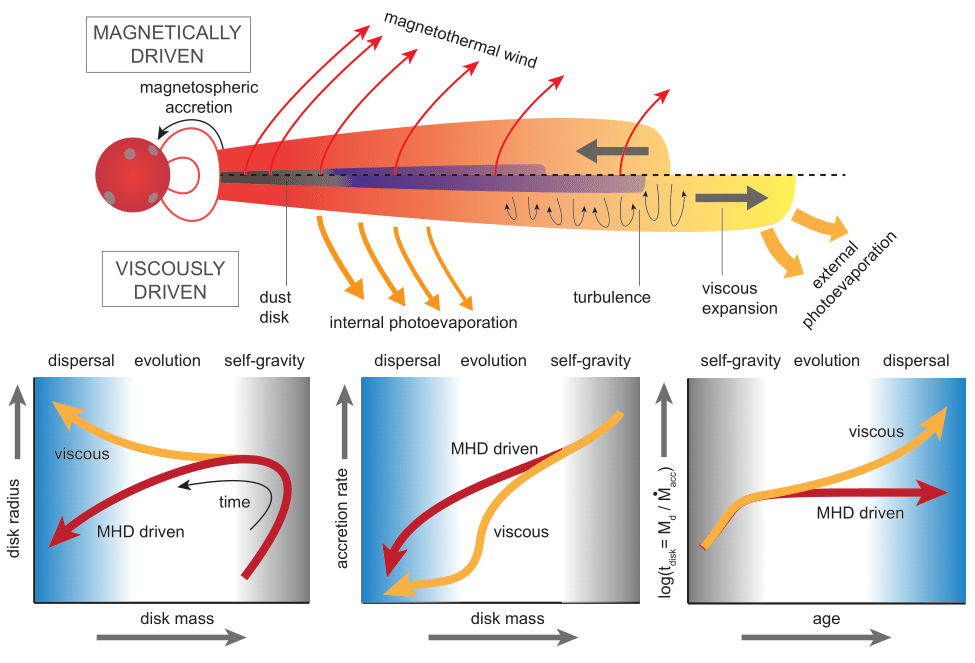
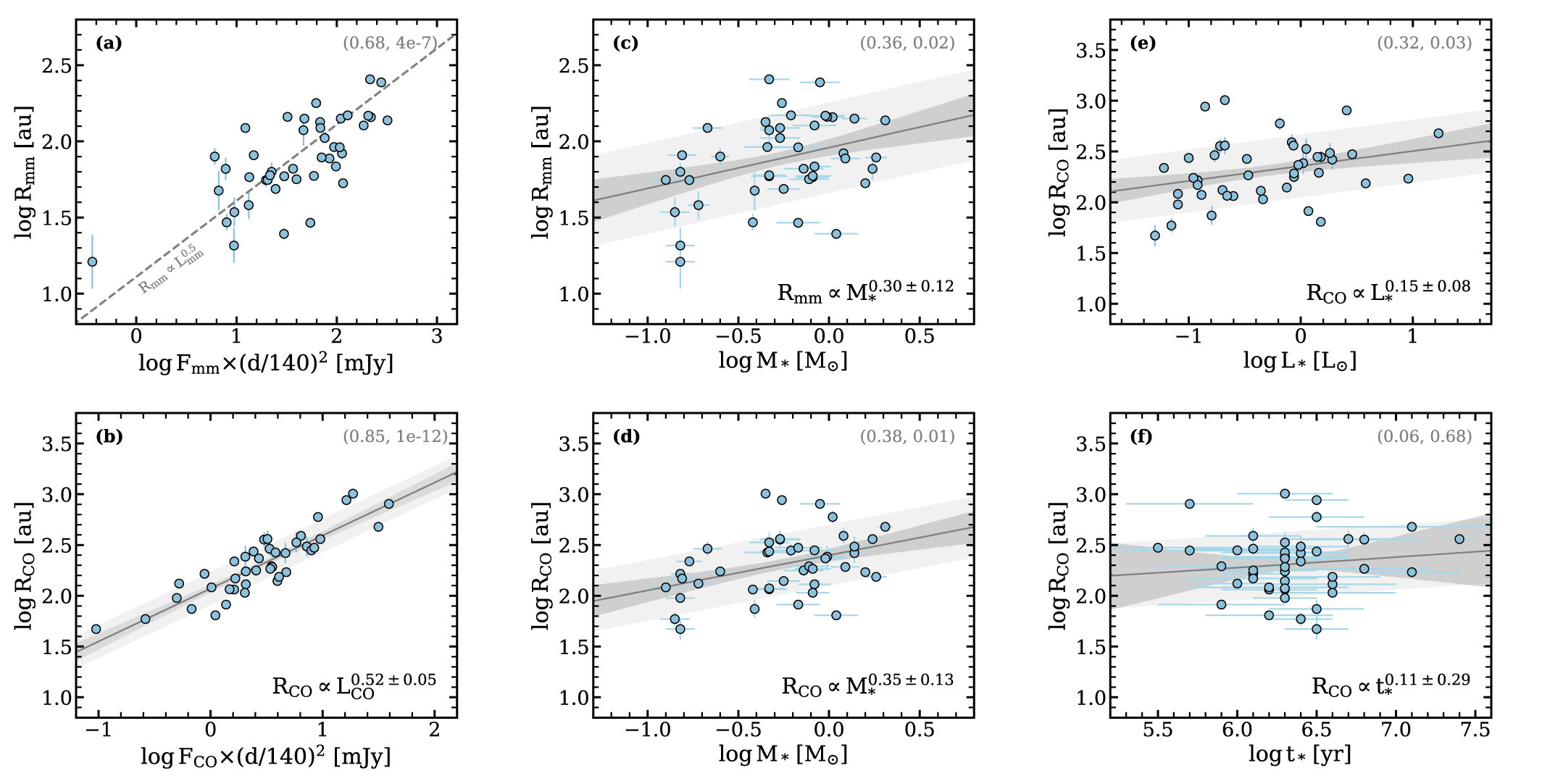
Long et al. 2022

Angular momentum budget

Large scatter of ang. mom.
Increasing specific angular momentum for increasing final stellar mass

Specific angular momentum computed from all accreting tracer particles at the first snapshot after star formation

subtle correlation with mass (inherited by disks??)

"We find marginal relationships between disk sizes and M*." (Long+ 2022)

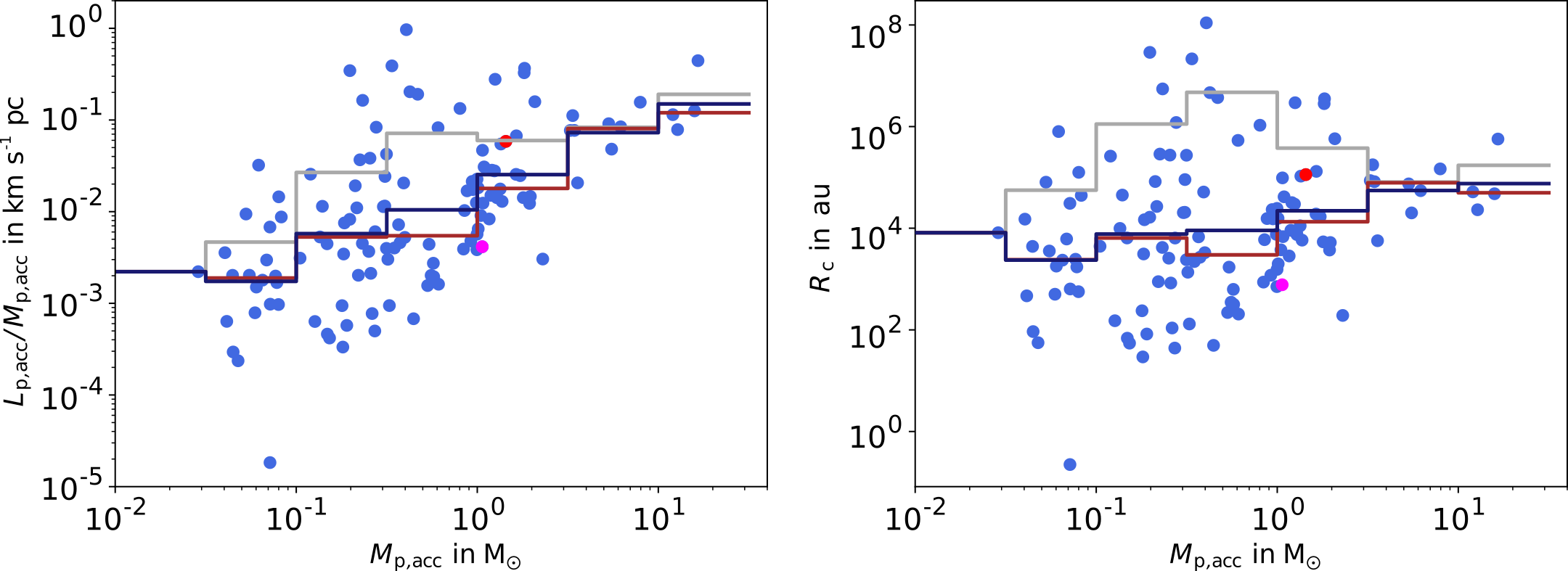
Küffmeier, Jensen & Haugbølle '23

Long et al. 2022

see also Padon et al. 2025, Winter et al. 2024

On average, stars with increasing final mass undergo prolonged infall

Orientation of star-disk systems can change substantially

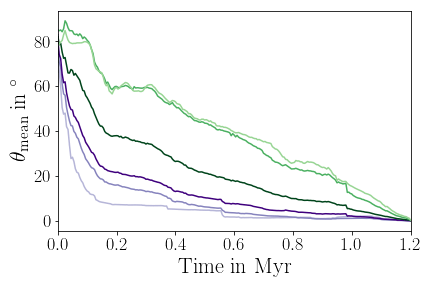
Orientation of infall

Küffmeier, Pineda, Segura-Cox & Haugbølle 2024

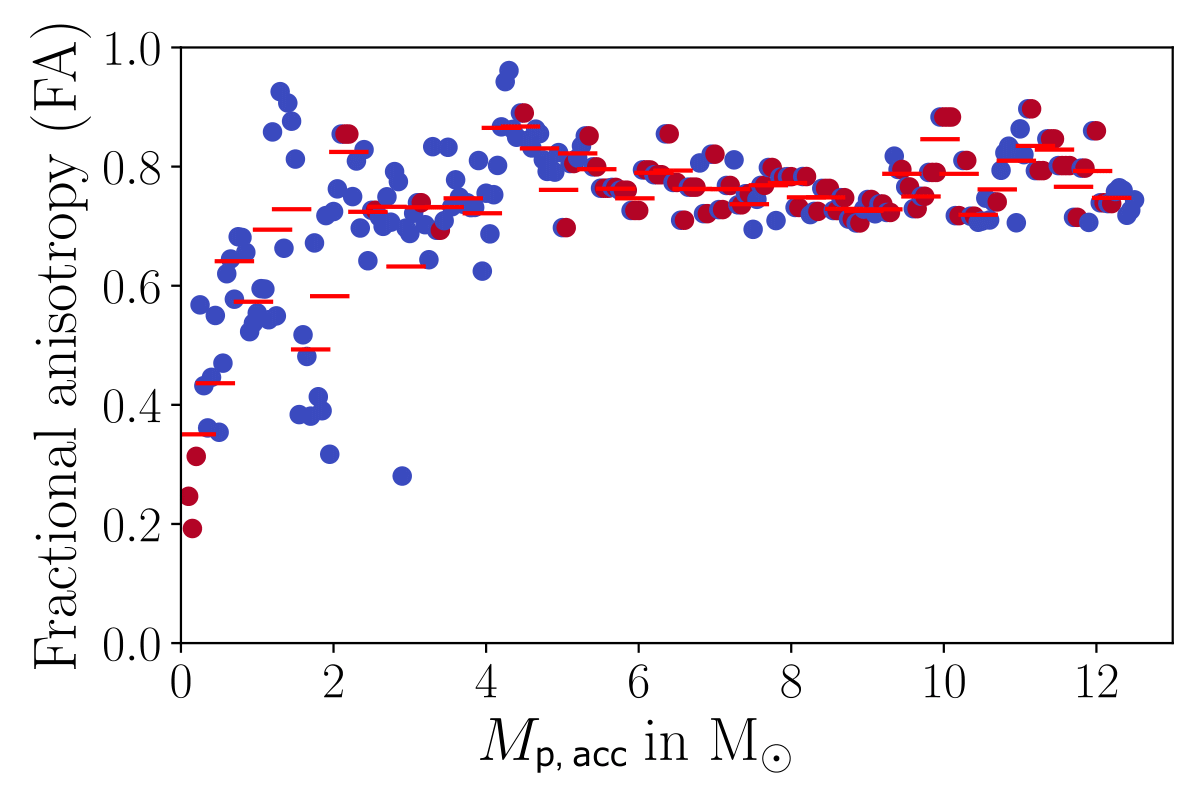
How to quantify anisotropy of accretion?

FA = 0: perfectly isotropic accretion

FA = 1: maximally anisotropic accretion

Fractional anisotropy based on tracer particles

Post-collapse infall is more anisotropic than initial collapse

Post-collapse accretion phase resembles Bondi-Hoyle

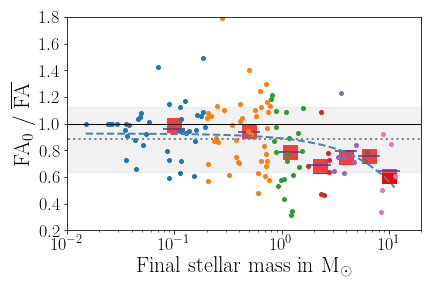
Küffmeier, Pineda, Segura-Cox & Haugbølle 2024

Post-collapse infall is more anisotropic than initial collapse

Anisotropic accretion

FA = 0: perfectly isotropic accretion

FA = 1: maximum anisotropic accretion

Küffmeier, Haugbølle, Pineda & Segura-Cox 2024

Late infall is more anisotropic than early collapse

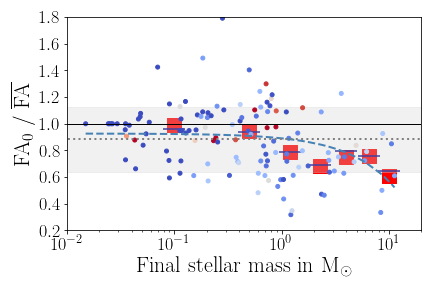
\mathrm{FA} = \sqrt{ \frac{1}{2}} \frac{\sqrt{(\lambda_1 - \lambda_2)^2 + (\lambda_2 - \lambda_3)^2 + (\lambda_3 - \lambda_1)^2}}{\sqrt{\lambda_1^2 + \lambda_2^2 + \lambda_3^2}}

Fractional anisotropy (FA) serves as a good measure for the (an-)isotropy of accretion.

FA=0: perfectly isotropic accretion, FA=1: maximally anisotropic

\frac{\Delta t_{\rm single}}{\Delta t_{\rm single}+\Delta t_{\rm mult}}

FA can also be a useful measure to compare (an)isotropy of stellar spins in clusters

Streamers (and shadows) as signs of infall

Formation of misaligned configuration

Observable as shadows in outer disk

Küffmeier, Dullemond, Reissl & Goicovic 2021

SU Aur (Ginski et al. 2021)

300 au

Krieger, Küffmeier et al. 2024

Do we really know disk "lifetimes"?

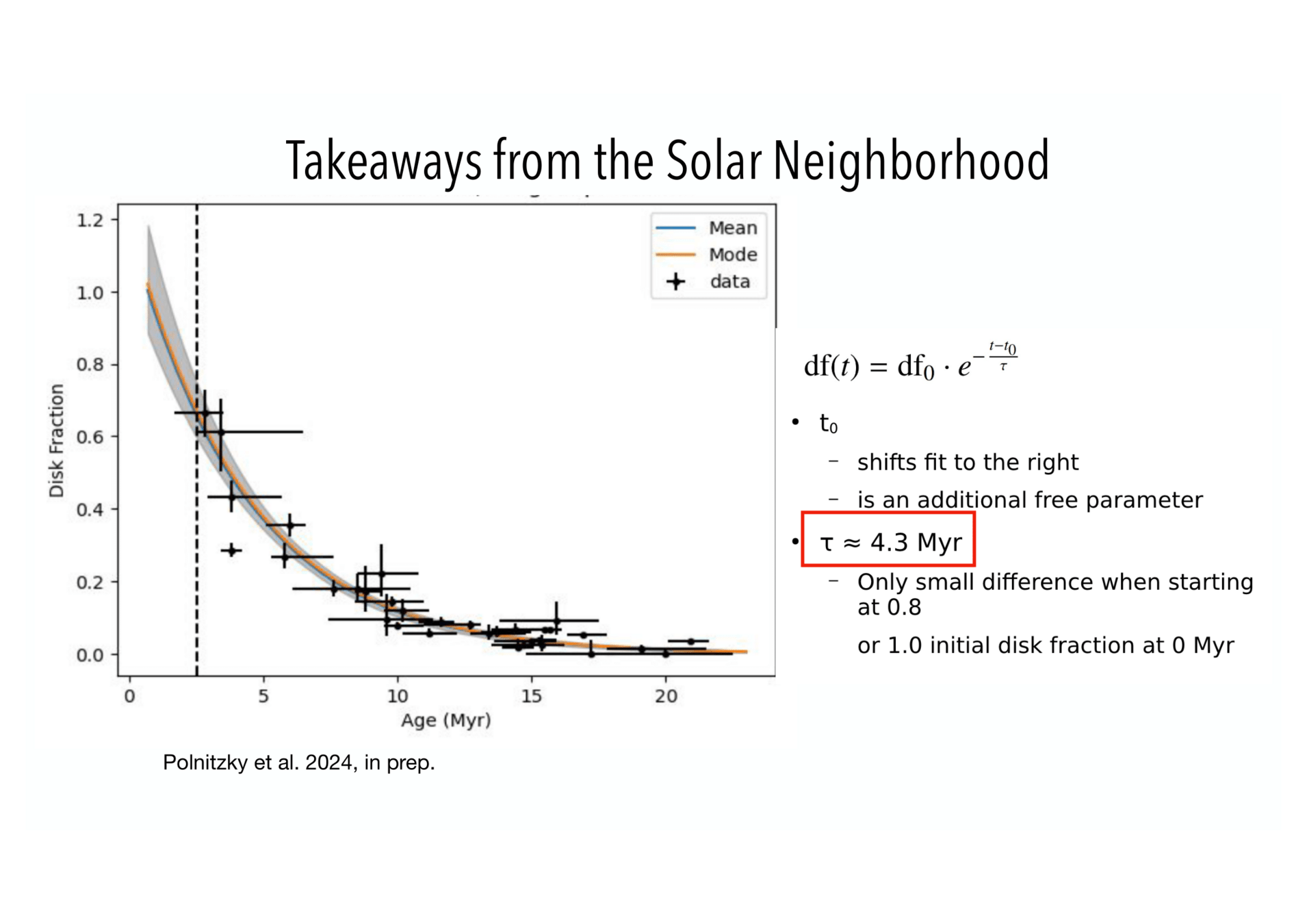
Polnitzky et al. 2024 in prep

Fraction reflecting occurrence of infall events instead of disk age?

Open questions and preliminary results

Credit: NASA/ESA Hubble space telescope &

ALMA (ESO/NAOJ/NRAO)

The big challenge:

link planet to star formation

50 au

Zoom-in on embedded stars

Küffmeier et al.

2019

Küffmeier et al. 2018

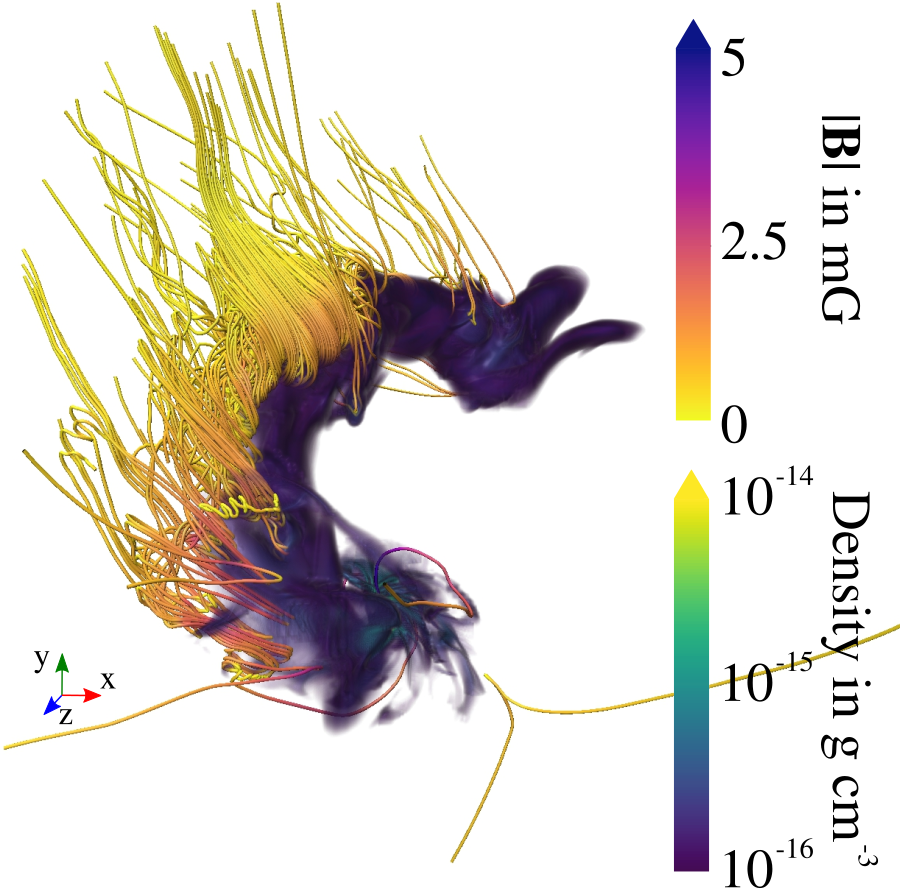
Küffmeier, Reißl et al. 2020

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

~1500 AU

Pro: self-consistent initial and boundary conditions for star formation

Con: computationally more expensive, more difficult analysis

for a similar concept, see also Lebreuilly et al. 2024, Yang & Federrath 2025

Zoom-in simulations

Christian G. Holm

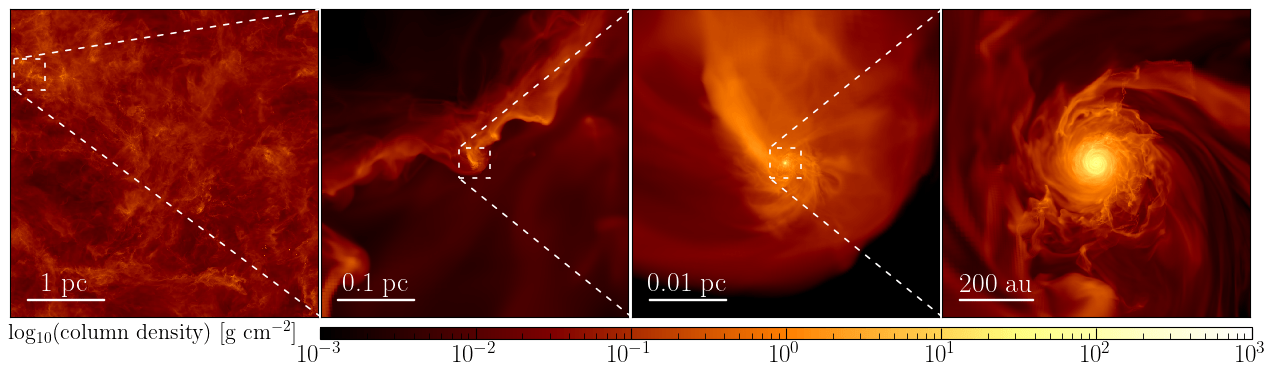
Zoom-in simulation*, ~1 au resolution in disk, barotropic equation of state

*(starting from previous RAMSES simulations and run with DISPATCH)

How does (early) infall shape disk formation?

Christian G. Holm

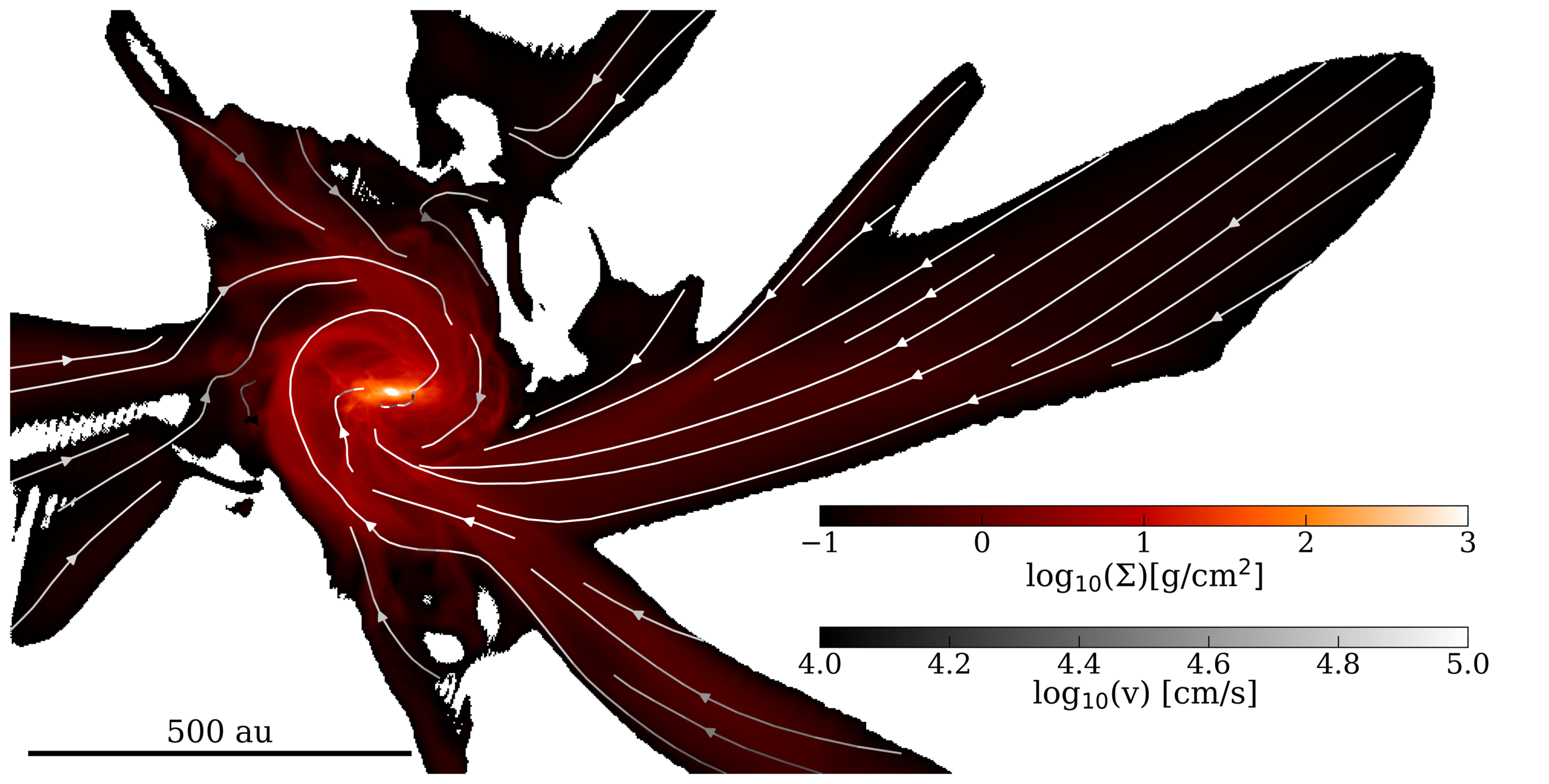
Zoom-in simulation, ~1 au resolution in disk, barotropic equation of state

Christian G. Holm

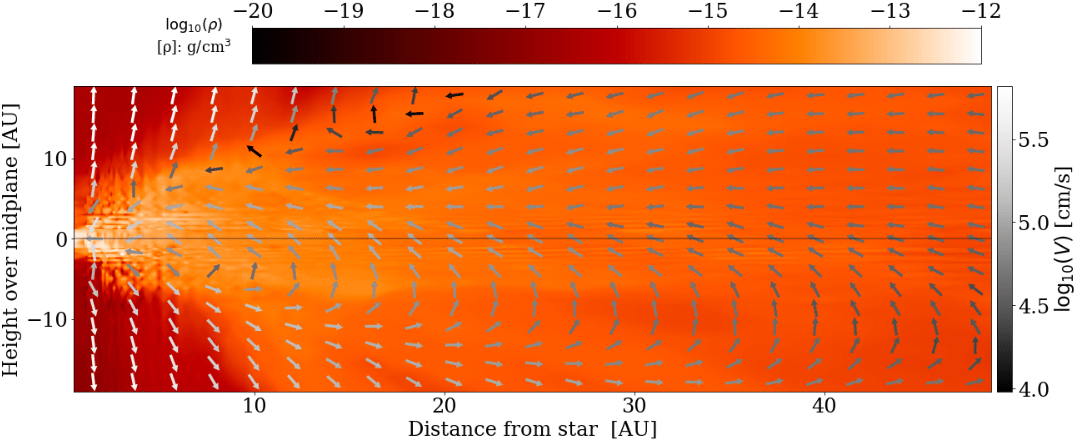
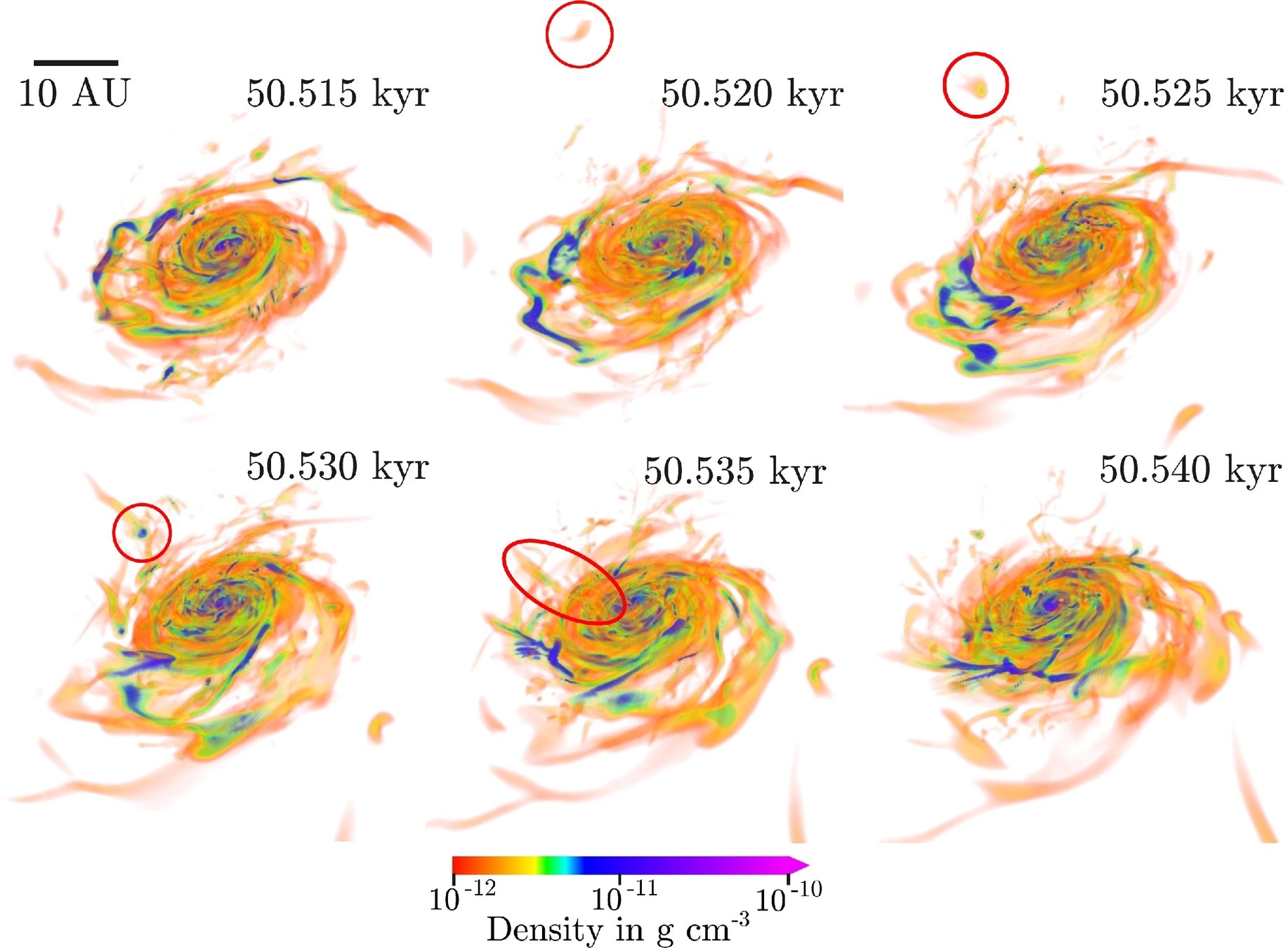
star A, t = 13 kyr

star A, t = 25 kyr

strong magnetic braking,

strong outflow

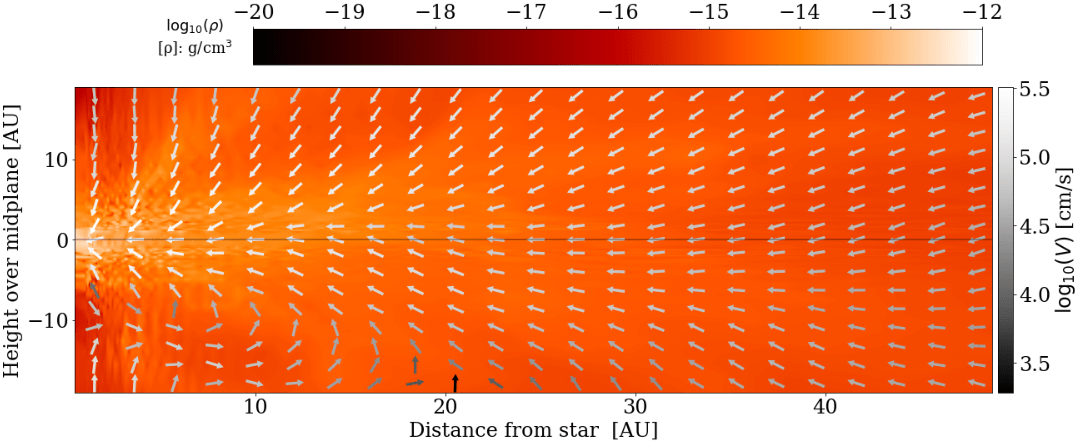
Gas accretes through the disk (little polar accretion)

Christian G. Holm

Gas accretes through the disk (little polar accretion)

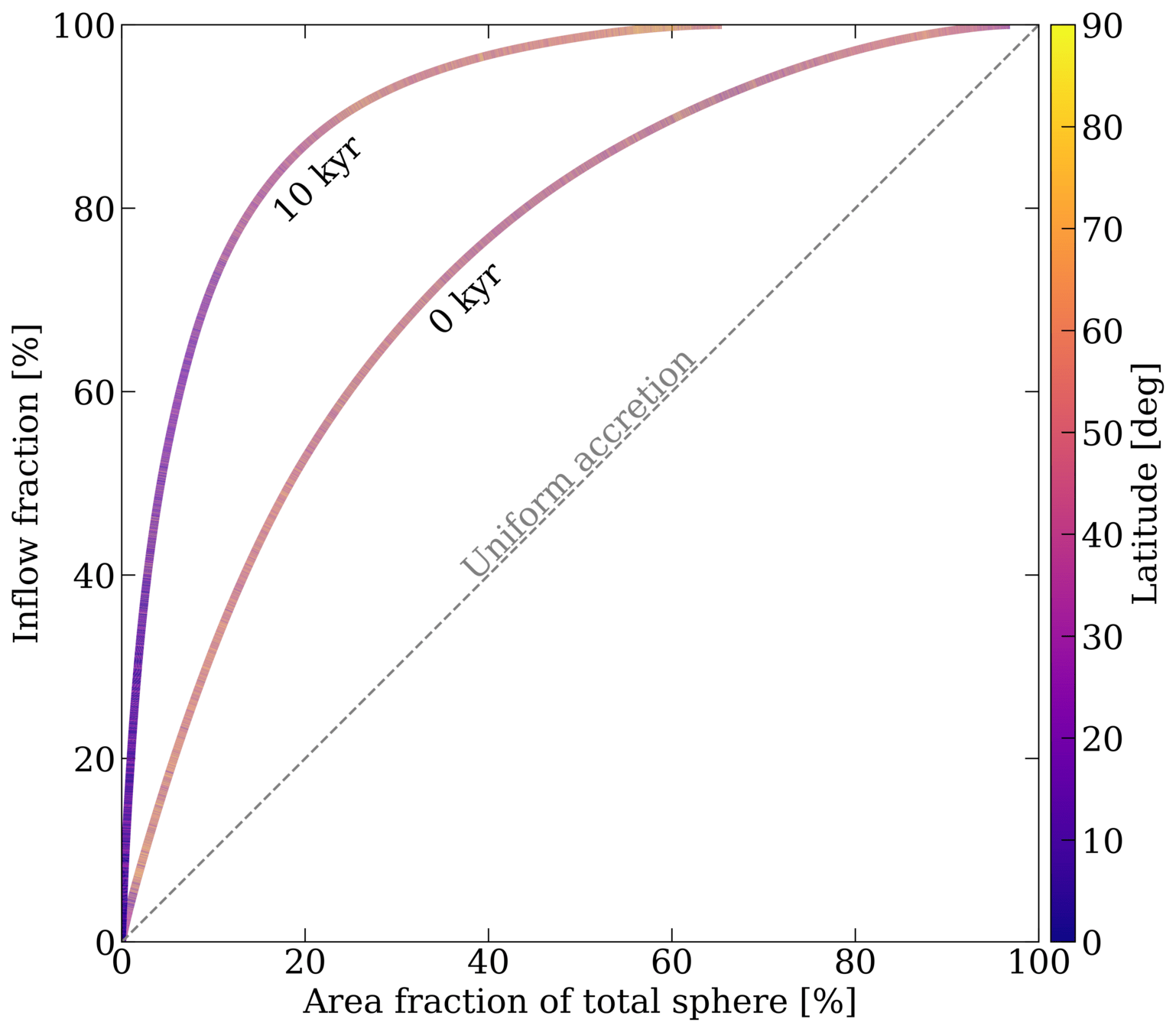
Young embedded disks

Christian G. Holm

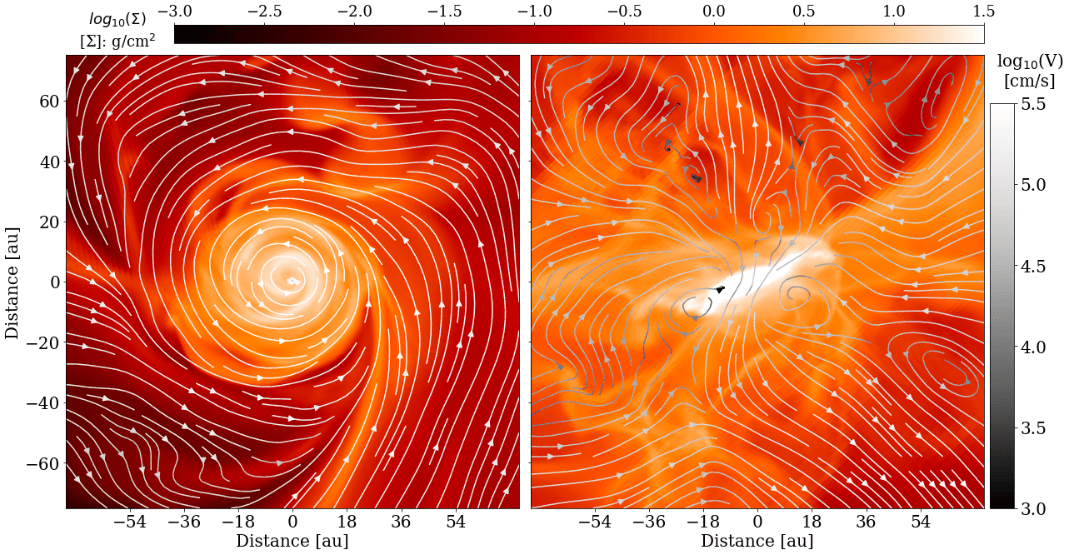
Zoom-in simulation*, ~1 au resolution in disk, barotropic equation of state

Christian G. Holm

How do outflows affect disk formation?

star A, t = 13 kyr

star A, t = 25 kyr

strong magnetic braking,

strong outflow

Prospect to compare with observations of outflows (e.g., ALMA-DOT, PI: Podio)

In progress: non-ideal MHD simulations and comparison with results by Lebreuilly et al. 2022

What fraction of the gas and dust returns to the disk after being ejected by an outflow?

Key question

Credit: Tsukamoto et al. 2021

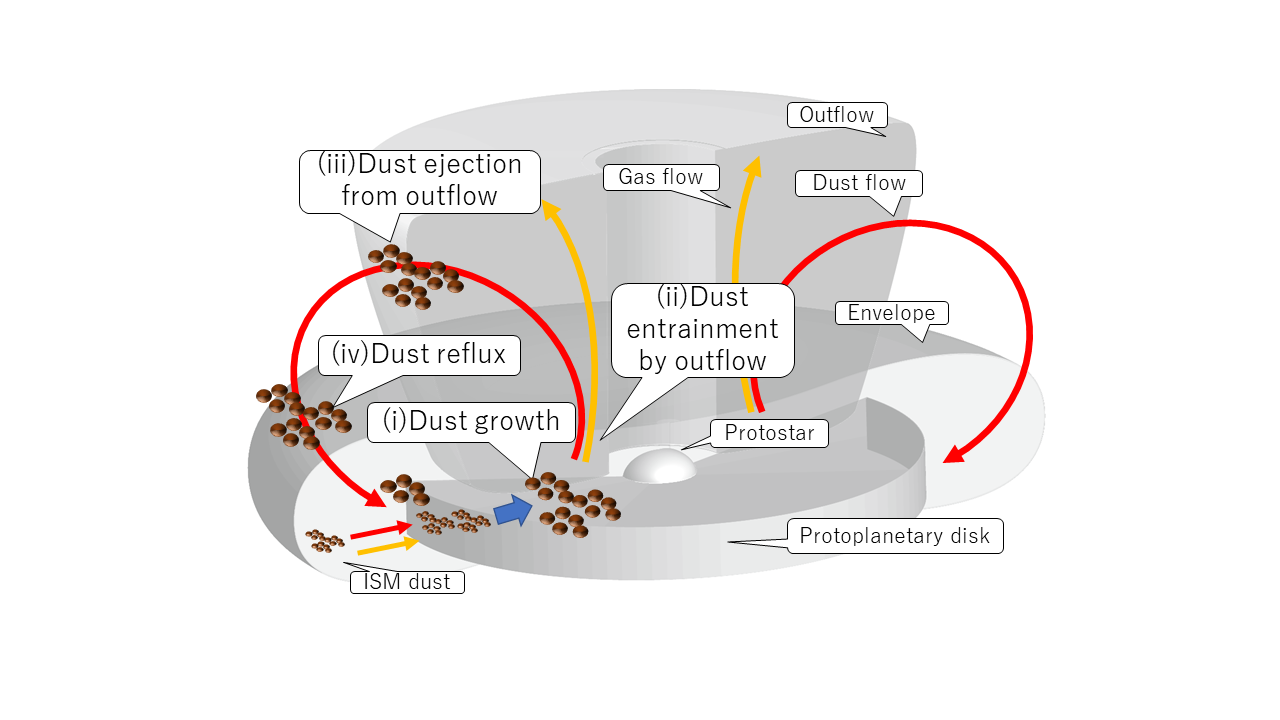
"Ash-fall" scenario aka conveyor belt

Increase in dust-to-gas ratio because dust can grow in disk and return

Tsukamoto et al. 2021

Upcoming work for DSTREAM

...solely replenishes the disk,

...plays an active role in triggering instabilities,

...induces dramatic changes such as misalignment.

III

DSTREAM will explore frequency and properties of infall onto star-disk systems that ...

images: A. Houge

Simulations: Holm, Haugbølle

Visualizations: Berlok

Summary

Disks are replenished, distorted or even destroyed by misaligned infall

Disks are dynamic entities

Star formation is a two-phase process consisting of mandatory initial collapse and post-collapse infall phase

Küffmeier 2024

Credit:

M. Lützen

EAS meeting Cork 2025, June 23-27

Symposium

Setting the stage for planet formation:

the importance of the environment for the evolution of protoplanetary discs

Special session

The chemistry of planet formation

Implications for Al-26 heterogeneity

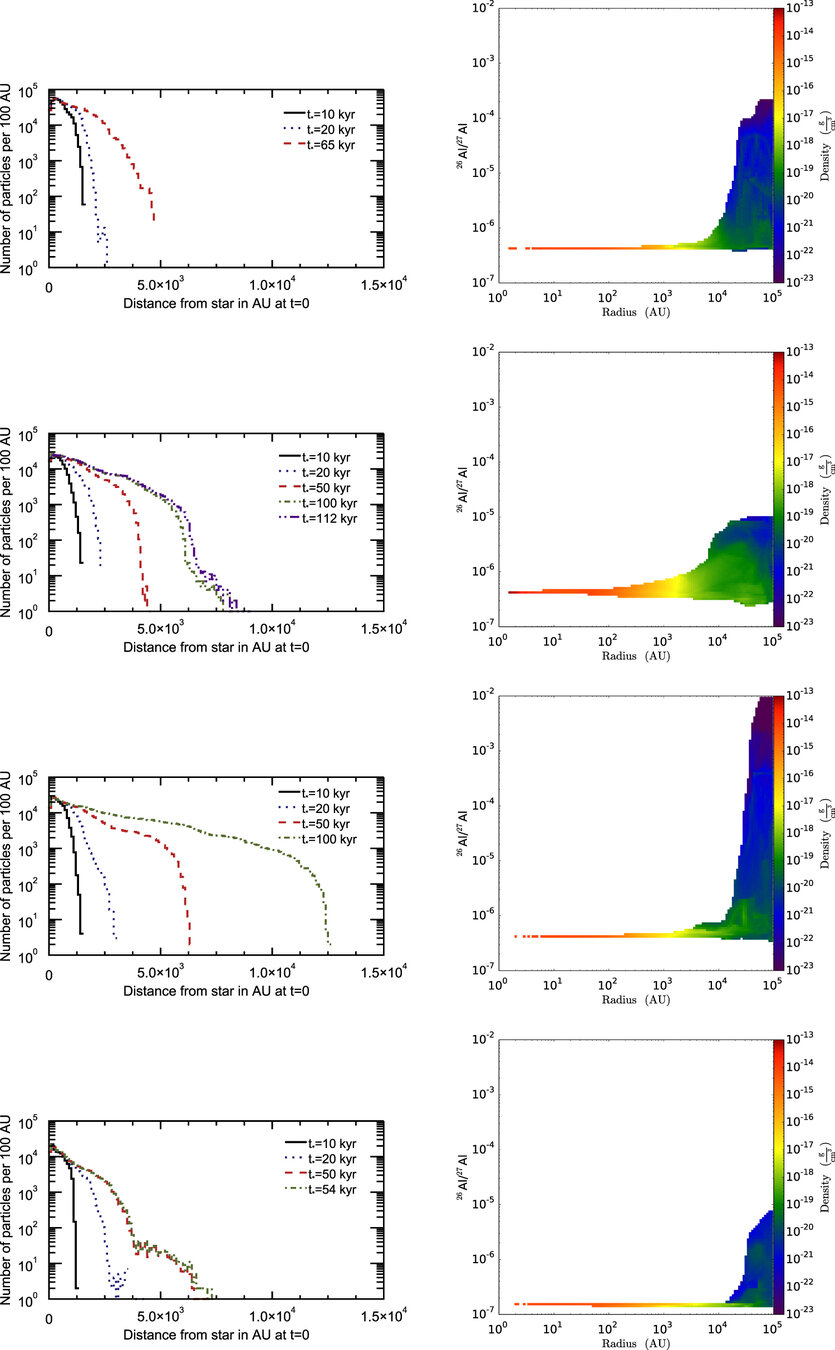
Küffmeier et al. 2016

Gas is well-mixed within core, and hence Al-26 abundance is fixed during CAI formation (t<~100 kyr).

BUT: significant deviations in Al-26 abundance beyond the core may likely be imprinted on disk afterwards!

Christian G. Holm

How do infall and outflow affect the disk?

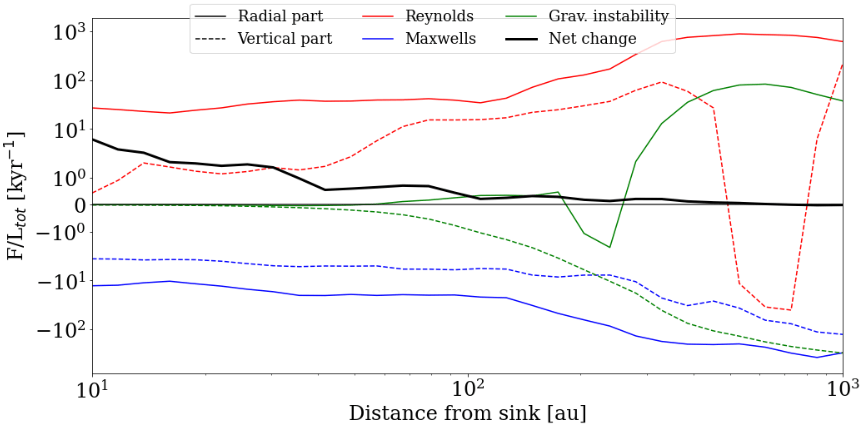
Angular momentum transport via magnetic braking

Zoom-in on embedded protostars

Küffmeier, Calcutt & Kristensen 2019

bridge structure similar to IRAS 16293--2422 (e.g. Sadavoy+ 2018, van der Wiel+ 2019, Maureira+ 2020)

Küffmeier, Reißl et al. 2020

~1500 AU

Küffmeier et al. 2018

magnetohydrodynamics

\frac{\partial \mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times\mathbf{B})

ideal MHD

\color{red}-\nabla\times[\eta_{\rm O} (\nabla \times \mathbf{B})]

\color{purple}-\nabla\times \{\eta_{\rm H} [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

\color{blue}-\nabla\times \{\eta_{\rm AD} \mathbf{B}/B \times [(\nabla \times \mathbf{B}) \times \mathbf{B}/B] \}

Ohmic dissipation

Hall

ambipolar diffusion

Non-ideal

Effect of ionization on disk size

increasing ionization rate

enhanced magnetic braking

smaller disks

see also Wurster et al. 2018

Küffmeier, Zhao & Caselli 2020