Topological and trivial gaps in graphene-based van der Waals heterostructures under strain and disorder
László Oroszlány
Department of Physics of Complex Systems, Eötvös Loránd University
and MTA-BME Lendület Topology and Correlation Research Group











Duncan and Kekulé
Charlie, Gene vs. August
Strained relationship

Kane, Mele, Phys. Rev. Lett. 95, 226801 (2005)
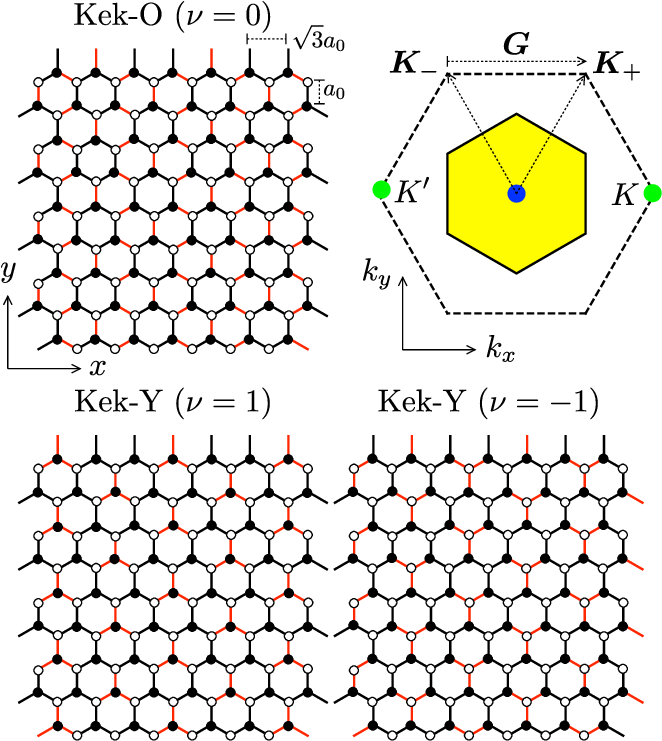
Act I
heterostructures, strain, gaps
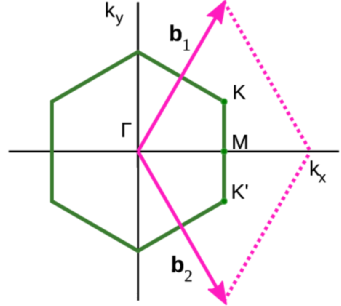
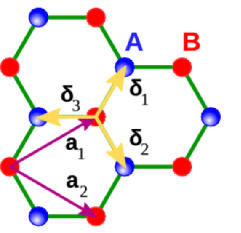
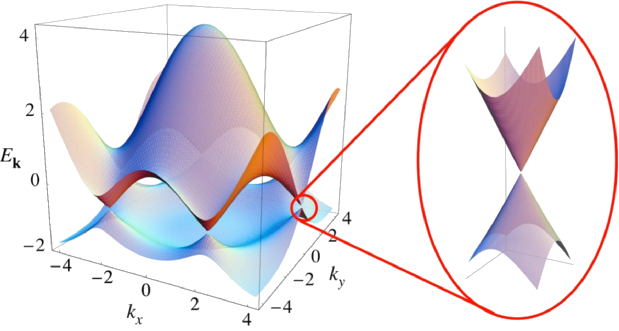
Graphene is ...
... a good template!
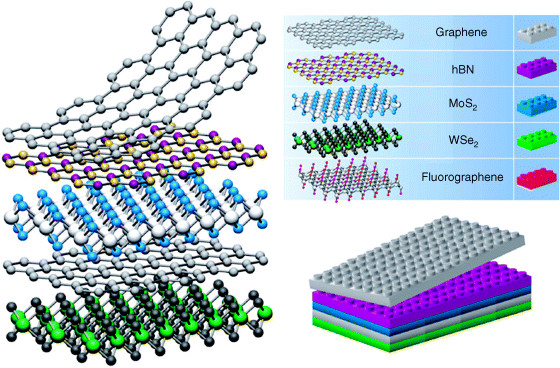
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
BiTeX: gigant spin-orbit coupling
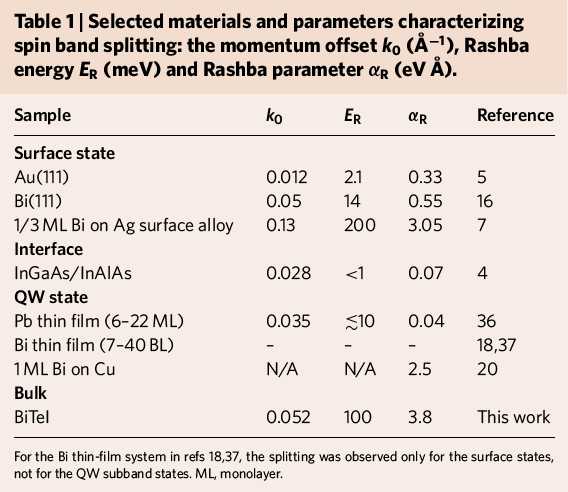
Ishizaka et al. Nature Materials 10, 521 (2011)
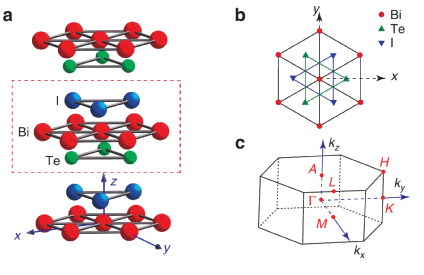
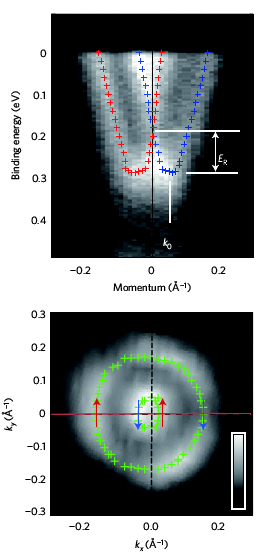

Fülöp et al. 2D Mater. 5, 031013 (2018)
Bulk
exfoliatin of a single trilayer
BiTeX/graphene heterostructures
Z. Tajkov el al. Nanoscale 11, 12704 (2019)
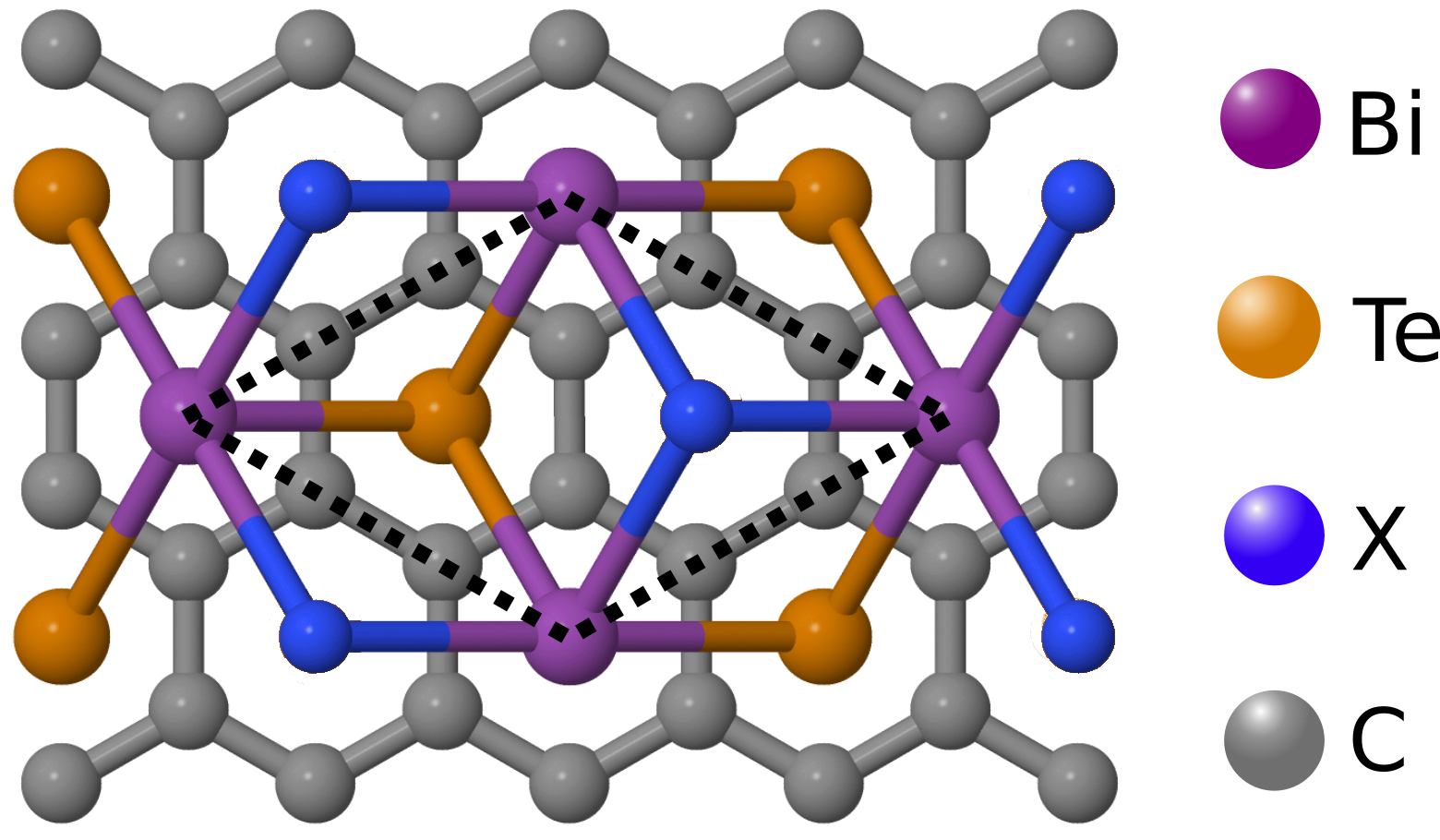
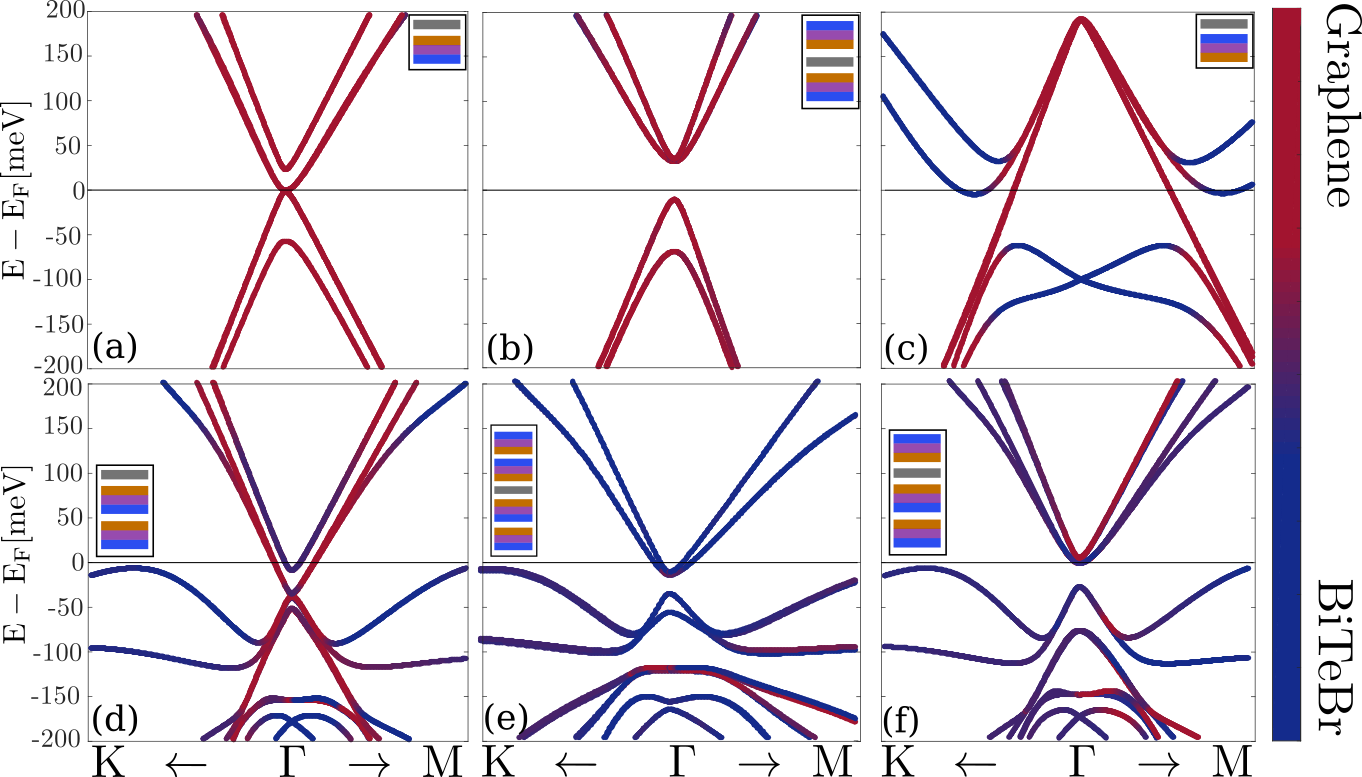
\(K \leftarrow \Gamma \rightarrow M \)



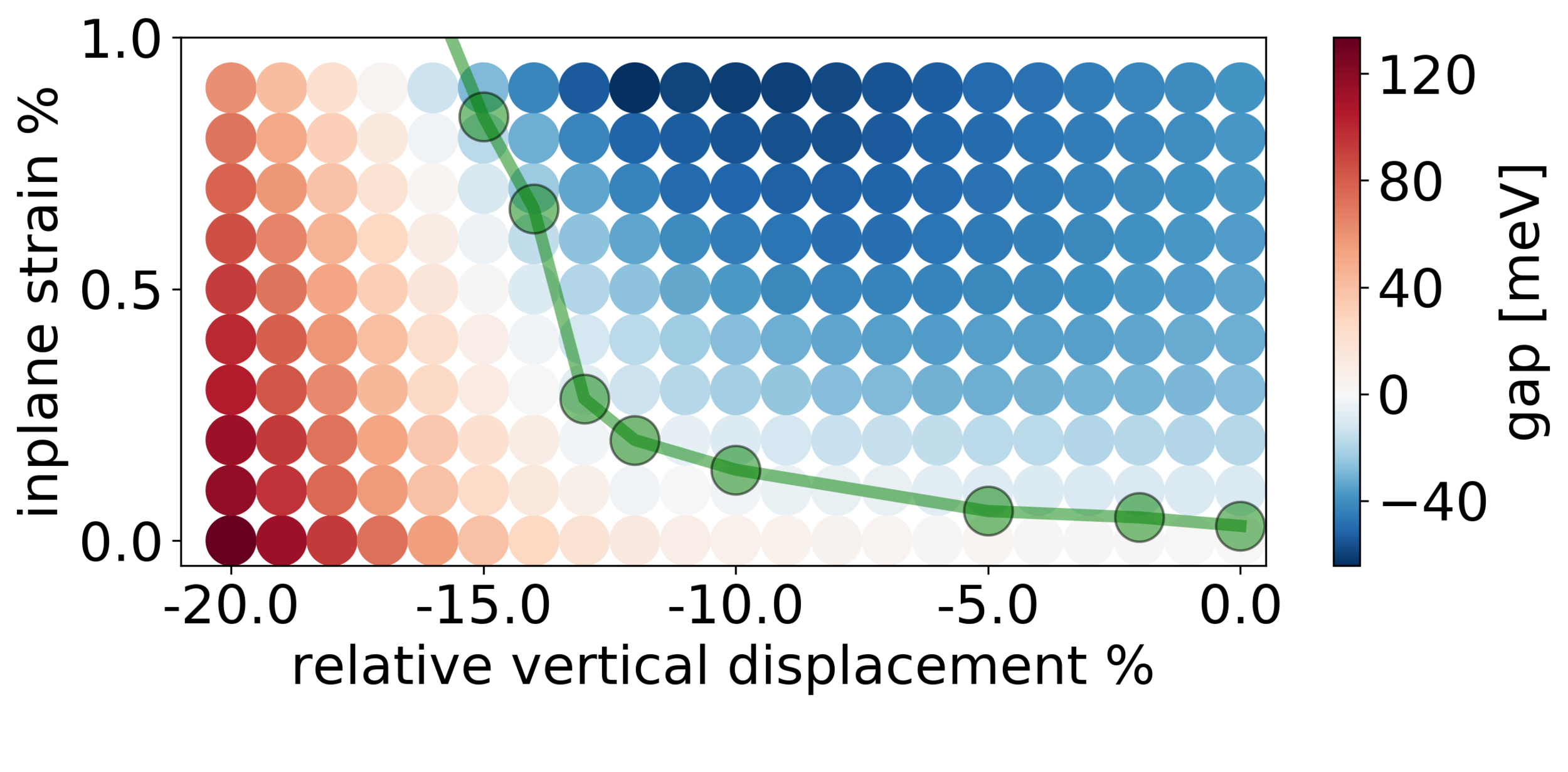
Pressure→I, inplane strain →TI !?!
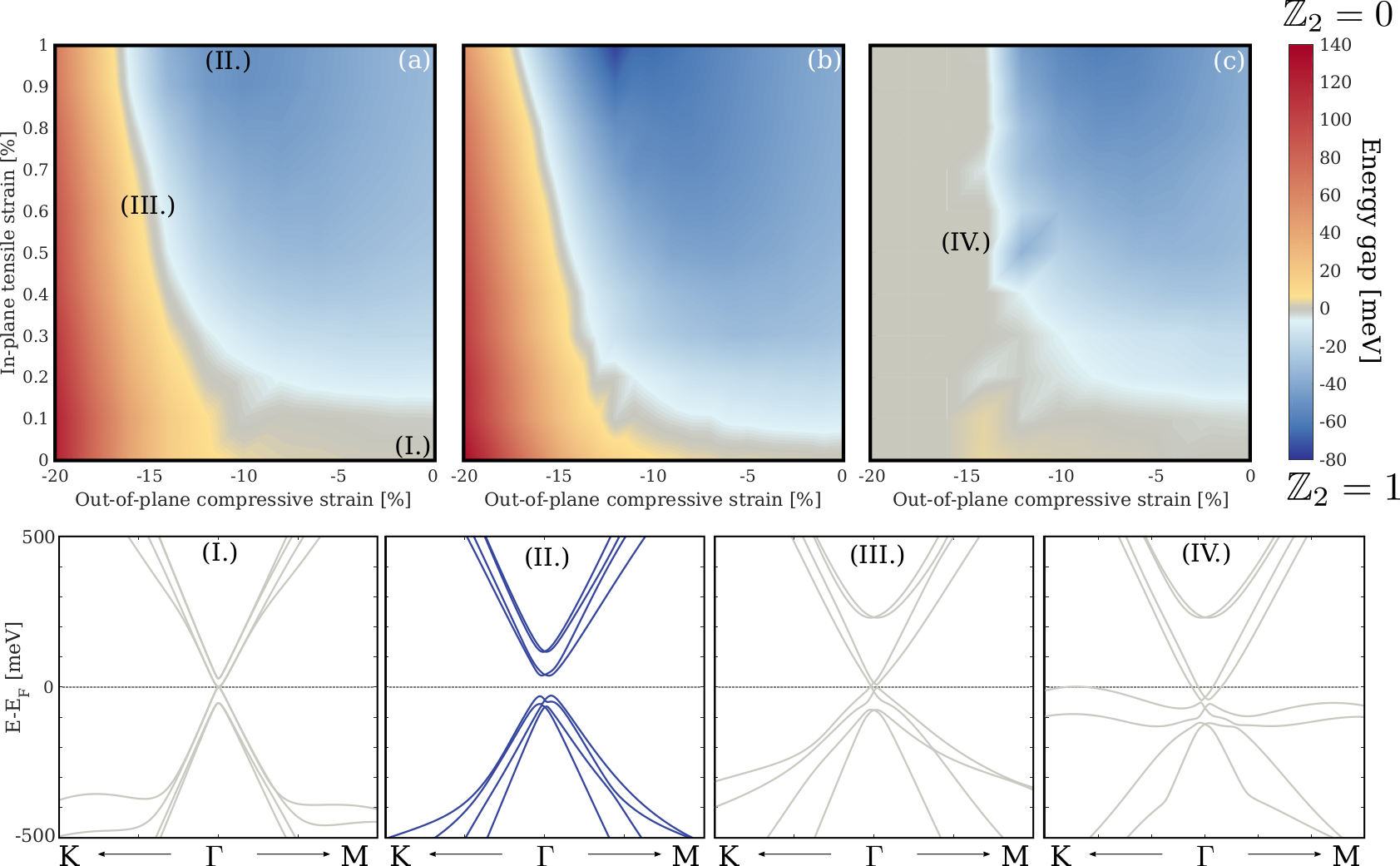
Z. Tajkov el al. Appl. Sci. 9, 4330 (2019)
BiTeBr
BiTeCl
BiTel
Effective model

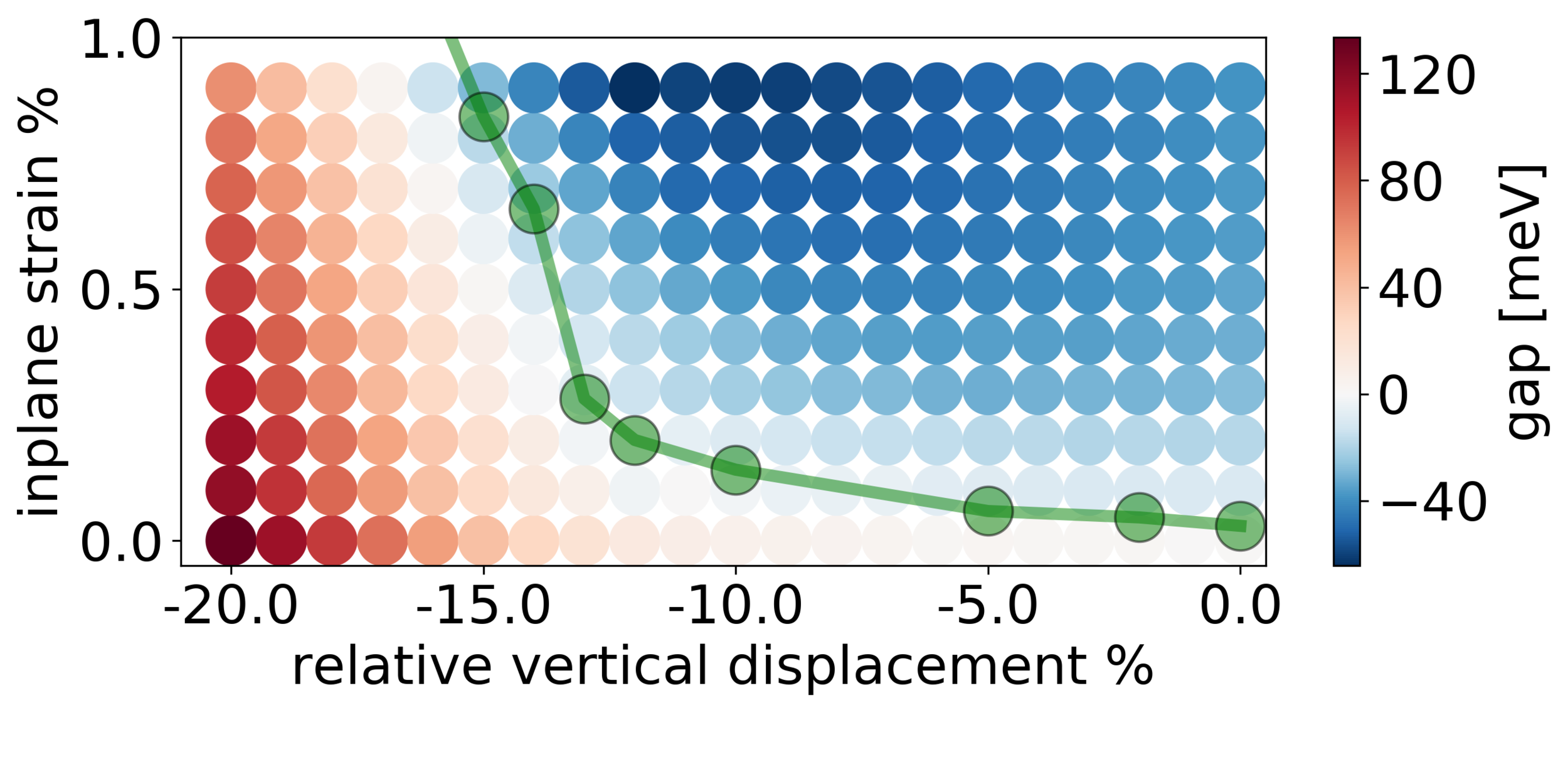
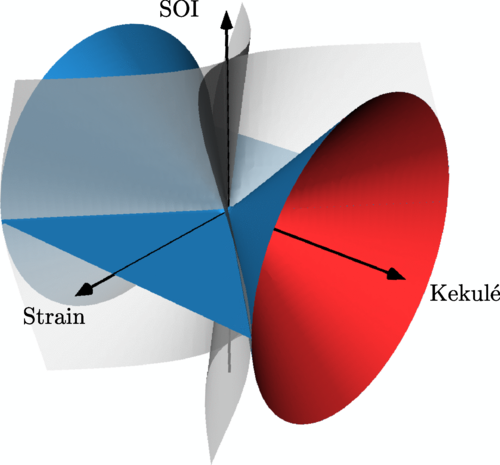
Tajkov el al. Phys. Rev. B 101, 235146 (2020)
take away message:
- Kekulé gap is killed by strain
- KM gap is insensitive to strain
low energy Dirac picture

Act II
A colorfull mess
Adatoms
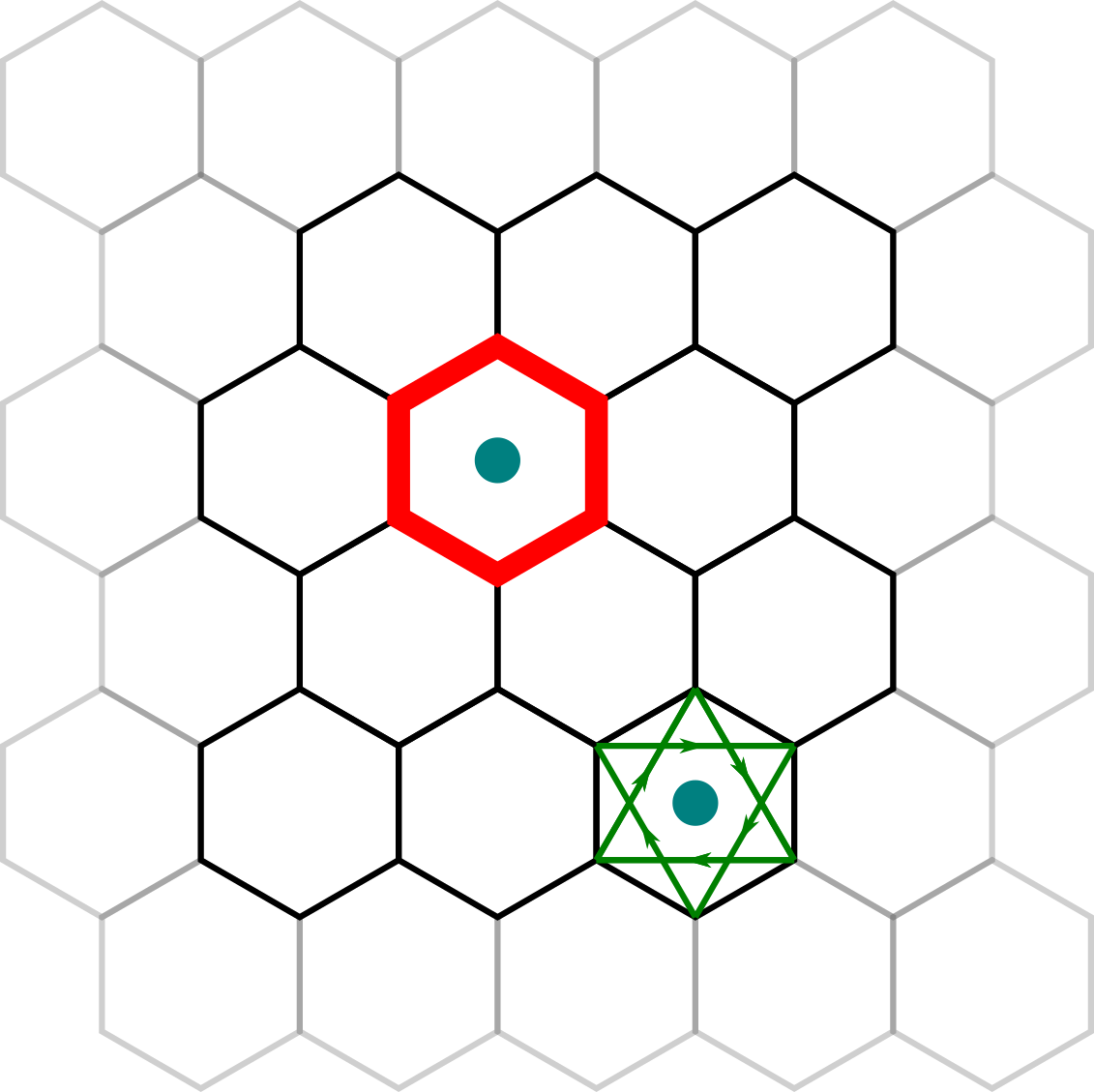
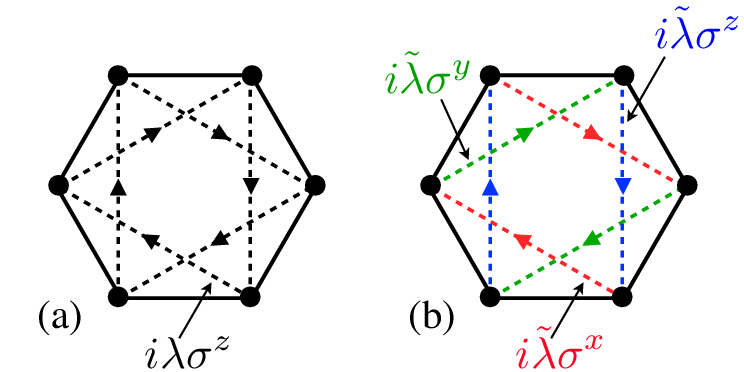
- adatoms distort the lattice, alter hopping around a hexagon
- adatoms introduce Kane-Mele type spin-orbit interaction on a plaquette
Promising candidates: Tl and dimers
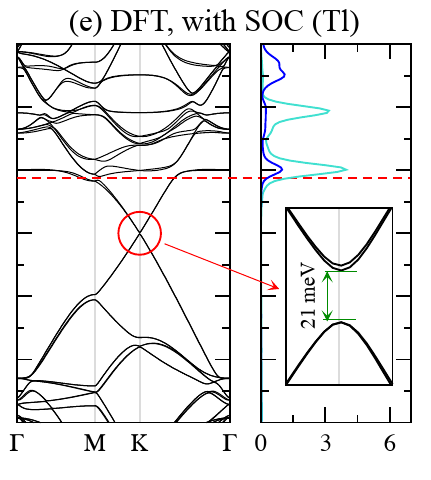
Phys. Rev. X 1, 021001 (2011)
Phys. Rev. Lett. 109, 266801 (2012)
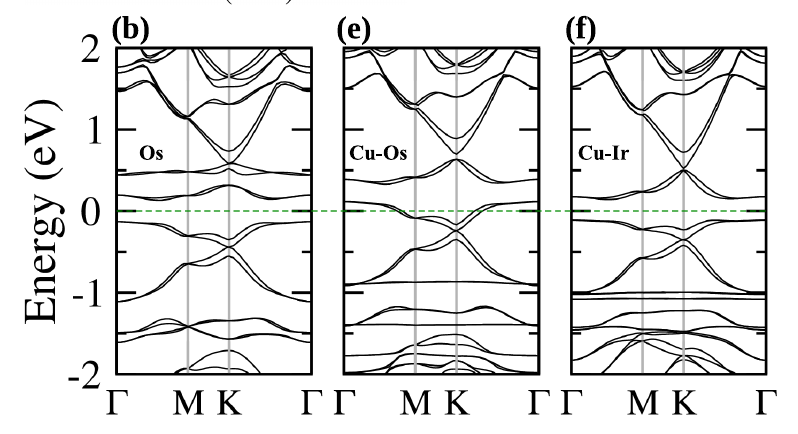
E[eV]
E[eV]
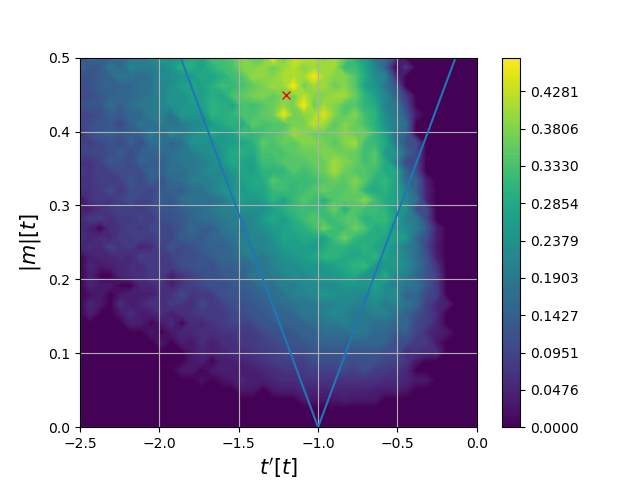
Hidden order of adatoms via RKKY
V.V.Cheianov et al. Solid State Commun. 149, 1499 (2009)
Large adatom \( \Rightarrow \) strong SOI

"Ferro"
"Para"
SOI does not interfere with ordering!
3 state Potts model

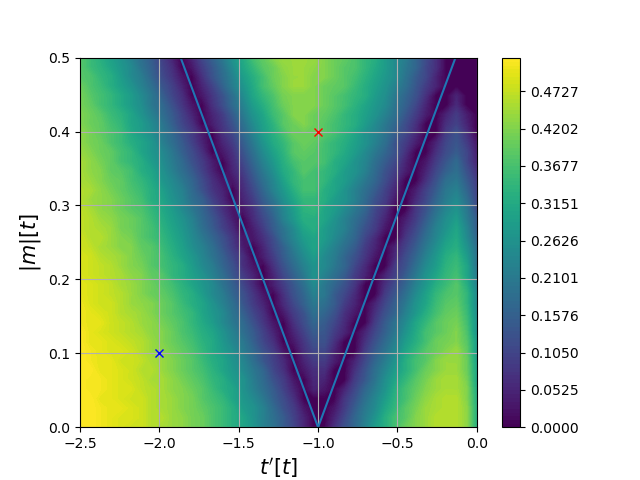
"Ferro"



"Para"
T

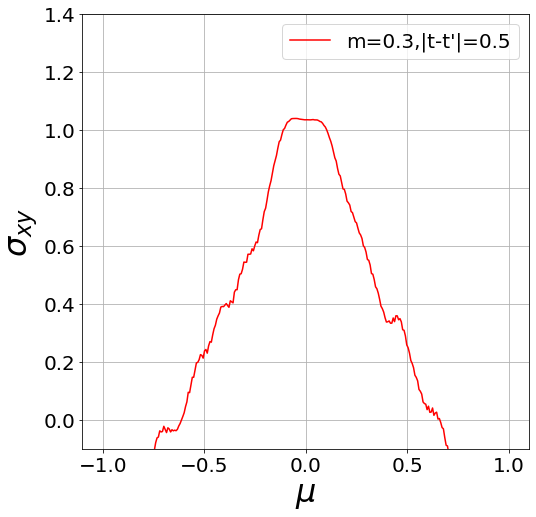
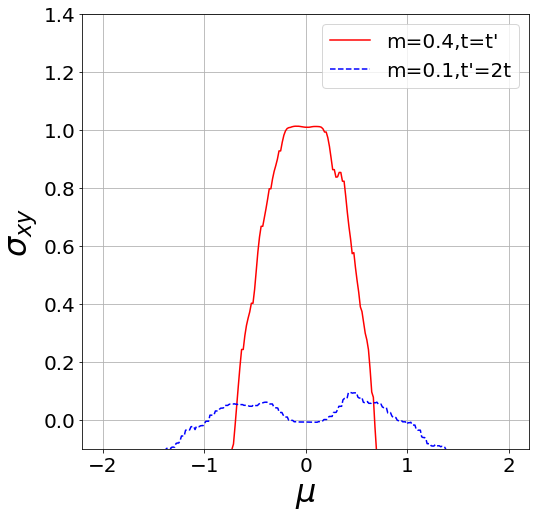
\(\sigma_{SH}\)
\(\sigma_{SH}\)
The Team




Zoltán Tajkov
Dániel Nagy
János Koltai
József Cserti

Balázs Dóra
Thanks!



Z. Tajkov el al. Nanoscale 11, 12704 (2019)
Z. Tajkov el al. Appl. Sci. 9, 4330 (2019)
Tajkov el al. Phys. Rev. B 101, 235146 (2020)