Relativistic Magnetic Interactions from a Nonorthogonal Basis Set

Eötvös Loránd University
Wigner Research Centre for Physics


László Oroszlány







The Team



- László Oroszlány, Zoltán Tajkov, János Koltai, Dániel Pozsár, Andor Kormányos, András Balogh, Tamás Véber, Marcell Sipos
-
Jaime Ferrer, Amador Garcia Fuente, Gabriel Martinez-Carracedo, Aurelio Hierro Rodriguez, Balázs Nagyfalusi, Rosa Eulalia González Ferreras
- Felix Büttner, Kai Litzius, Steffen Wittrock
- Efren Navarro-Moratalla, Marta Galbiati, Jose Joaquin Perez Grau
- László Szunyogh, László Udvardi, Bendegúz Nyári, Anjali Jyothi Bhasu



























Heisenberg model and DFT perturbation theory

DFT through
RKKR
&
Liechtenstein, Katsnelson , Antropov, Gubanov
J. Magn. Magn. Mater. 67 65 (1987)
Oroszlány, Ferrer, Deák, Udvardi, Szunyogh
Phys. Rev. B 99, 224412 (2019)
Single collinear scf calculation needed!
What is \(\delta \hat{V}_i\) ?
3) The definition of local operator
in a non-orthogonal basis needs
a pragmatic choice!
1) We need to rotate the magnetic moment!
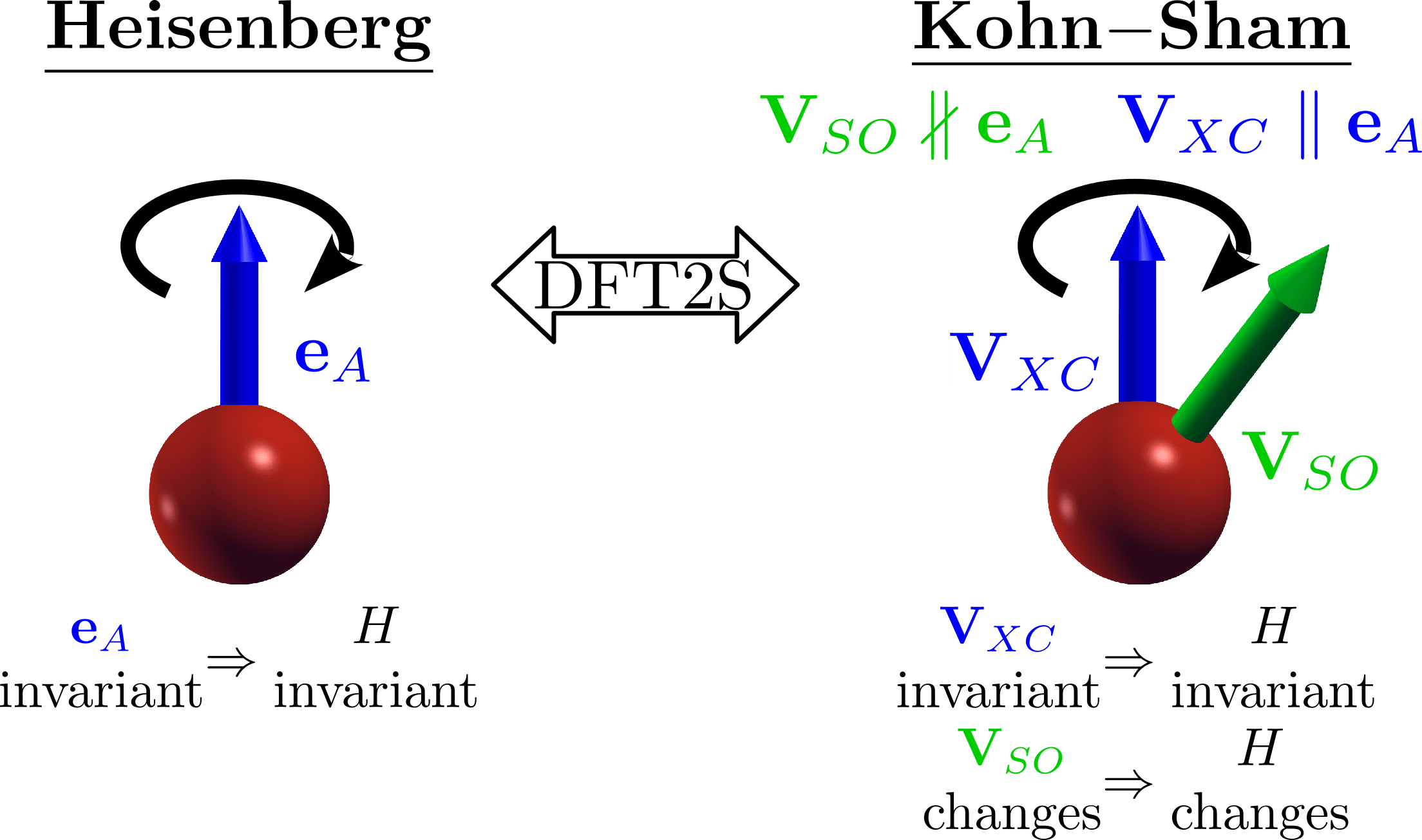
2) We need to identify the magnetic entity!
Could be:
- Single atom
- Cluster of atoms
- Certain orbitals inside an atom

Relativistic magnetic model parameters
Udvardi, Szunyogh, Palotás, Weinberger
Phys. Rev. B 68, 104436 (2003)
Martínez-Carracedo, Oroszlány, García-Fuente, Nyári, Udvardi, Szunyogh, Ferrer
Phys. Rev. B 108, 214418 (2023)
Istropic
exchange
Symmetric traceless exchange
Dzyaloshinskii - Moriya vector
On-site
anisotropy
Grogu
Multiple collinear reference states needed!
Single collinear scf calculation needed!
Fe, Co, Ni, KKR vs SIESTA
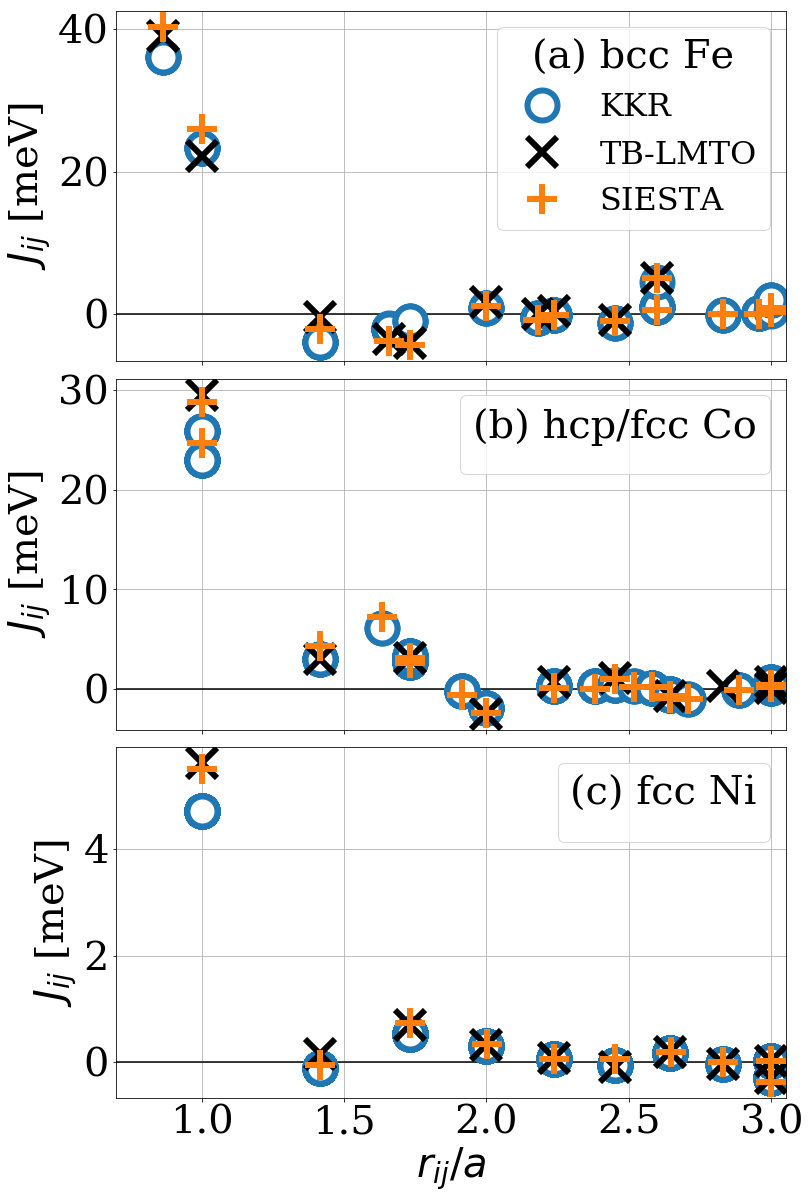
Oroszlány, Ferrer, Deák, Udvardi, Szunyogh;
Phys. Rev. B 99, 224412 ( 2019)
| SKKR | SIESTA | |
|---|---|---|
| Fe | 2.365 | 2.356 |
| Co | 1.542 | 1.580 |
| Ni | 0.675 | 0.626 |
\(\mu / \mu_B\)
| SKKR | TB-LMTO | SIESTA | Experiment | |
|---|---|---|---|---|
| bcc Fe | 1478 | 1414 | 1330 | 1044-1045 |
| hcp Co | 1504 | 1645 | 1490 | 1388-1398 |
| fcc Ni | 348 | 397 | 389 | 624-631 |
C\(_2\)F with SIESTA
A. N. Rudenko et al.
Phys. Rev. B 88, 081405 (2013)
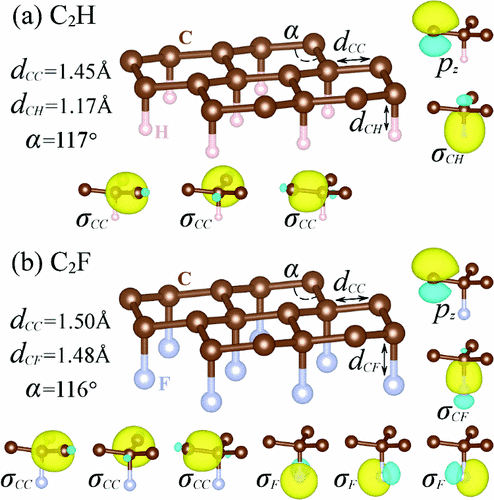
Oroszlány, Ferrer, Deák, Udvardi, Szunyogh; Phys. Rev. B 99, 224412 ( 2019)
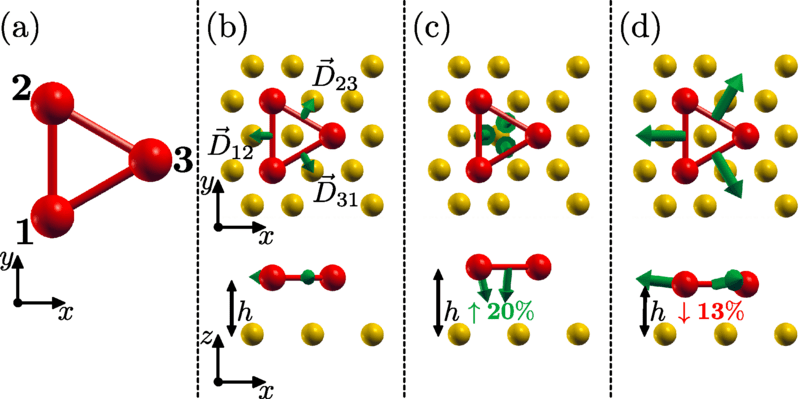
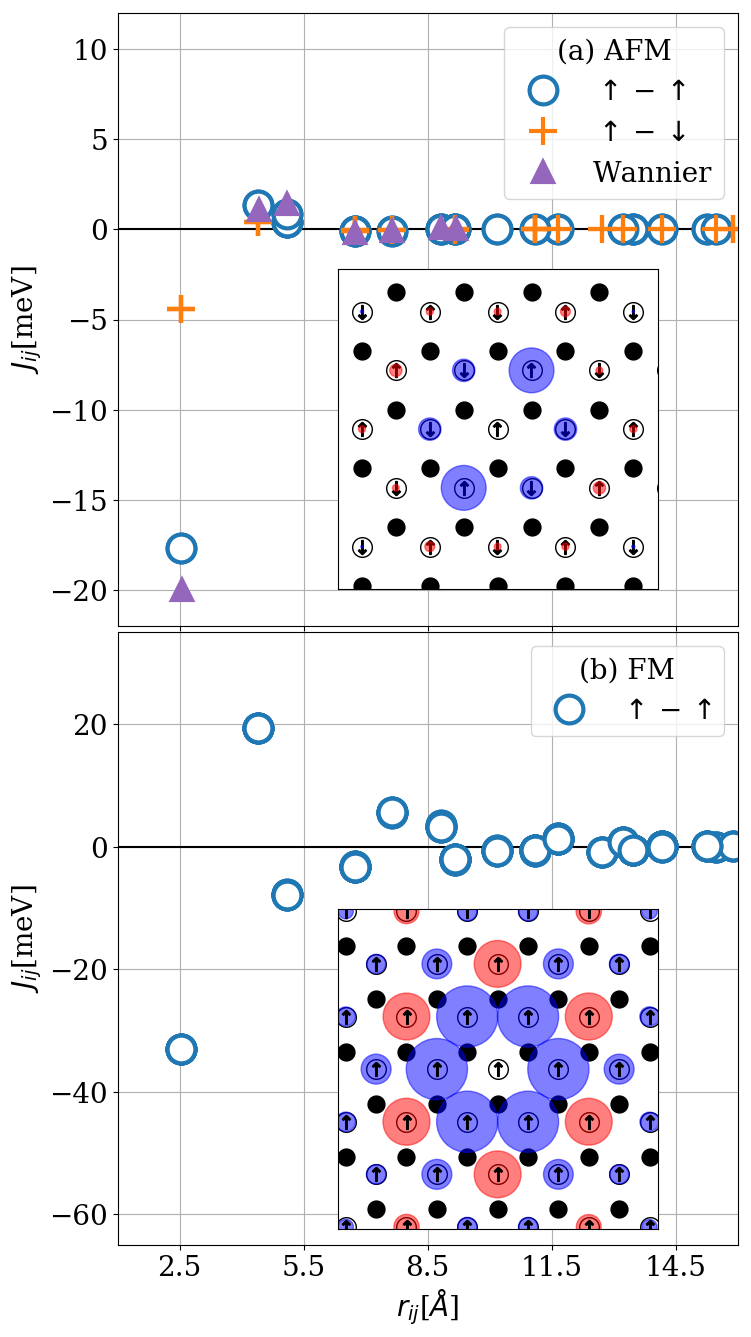
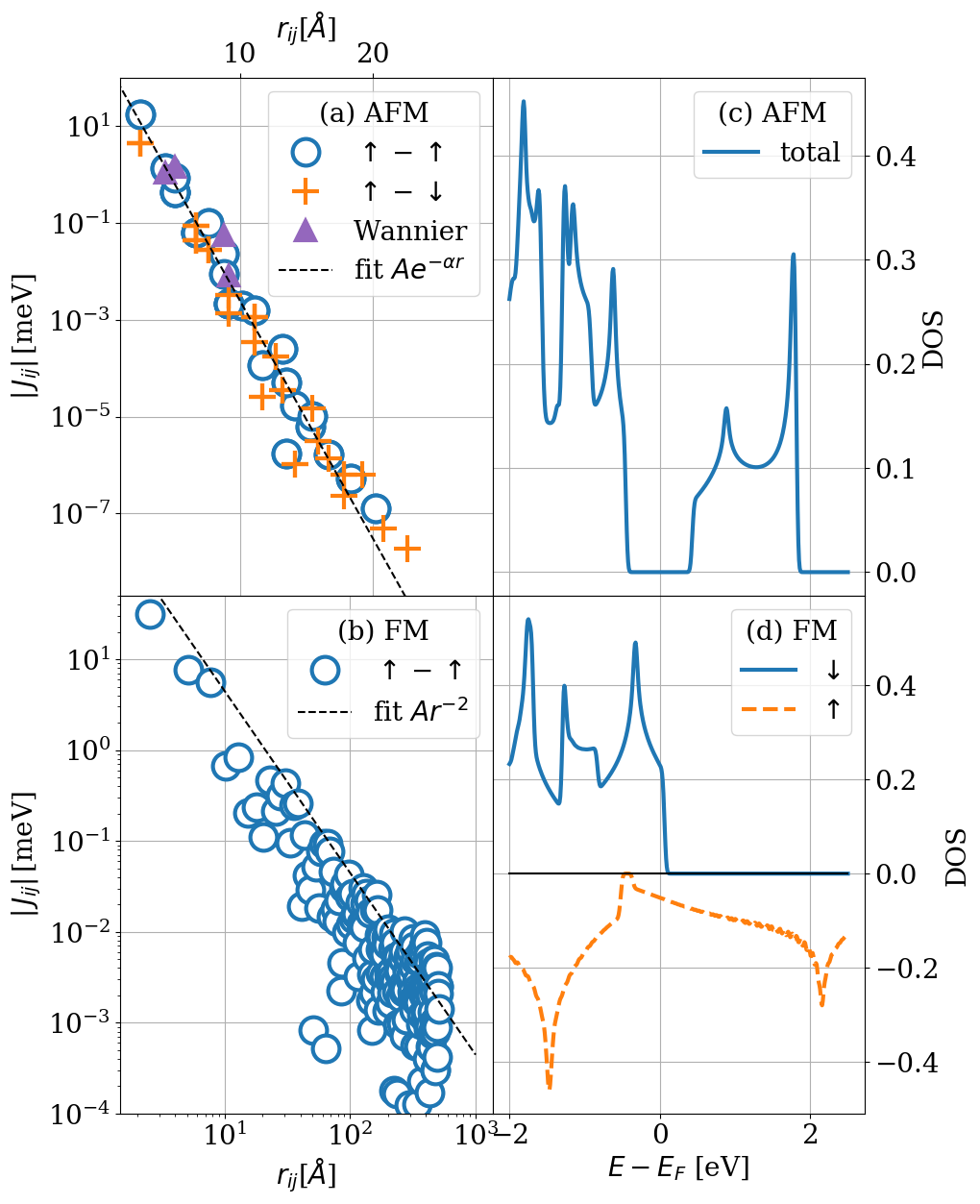
Cr trimer on top of Au [111]

Martínez-Carracedo, Oroszlány, García-Fuente, Nyári, Udvardi, Szunyogh, Ferrer Phys. Rev. B 108, 214418 (2023)
"simple" projection
"complicated"
projection
[meV]
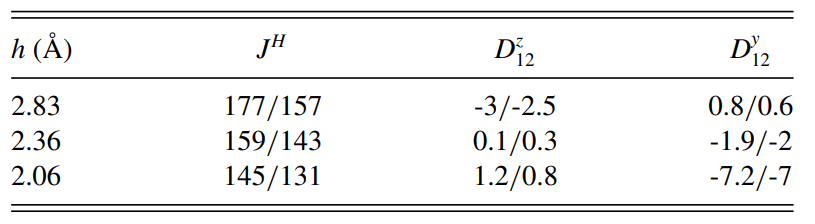
I. V. Solovyev Phys. Rev. B 107, 054442 (2023)
| meV | J | DM |
|---|---|---|
| 1nn | -0.34 | 0 |
| 2nn | -1.14 | 0.32' |
| 3nn | 0.65 | 0 |
\( K^{xx} \)-\( K^{zz} \)=0.47 meV
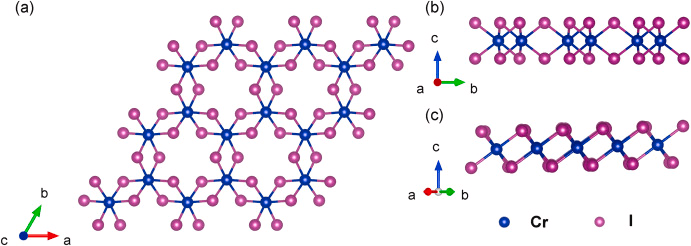
CrI\(_3\) benchmarks
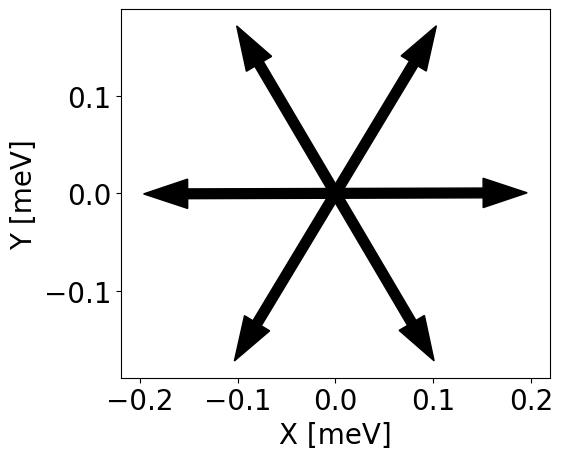
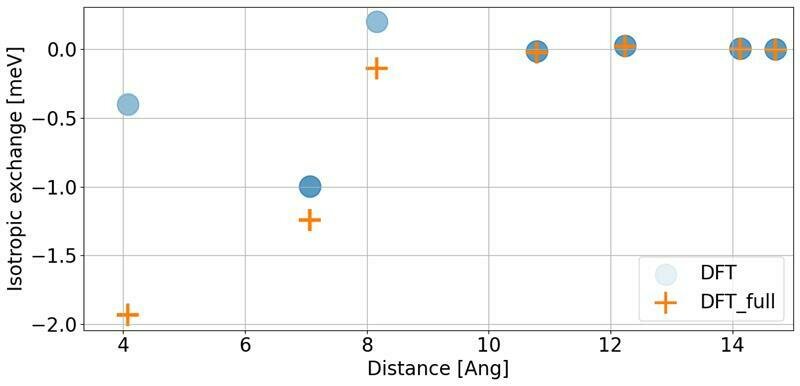
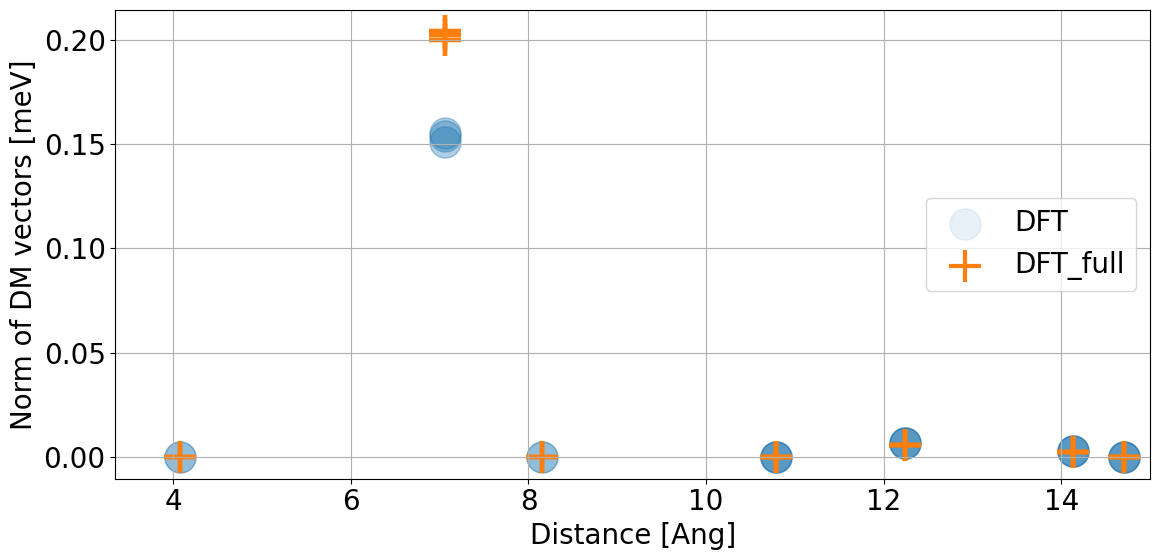
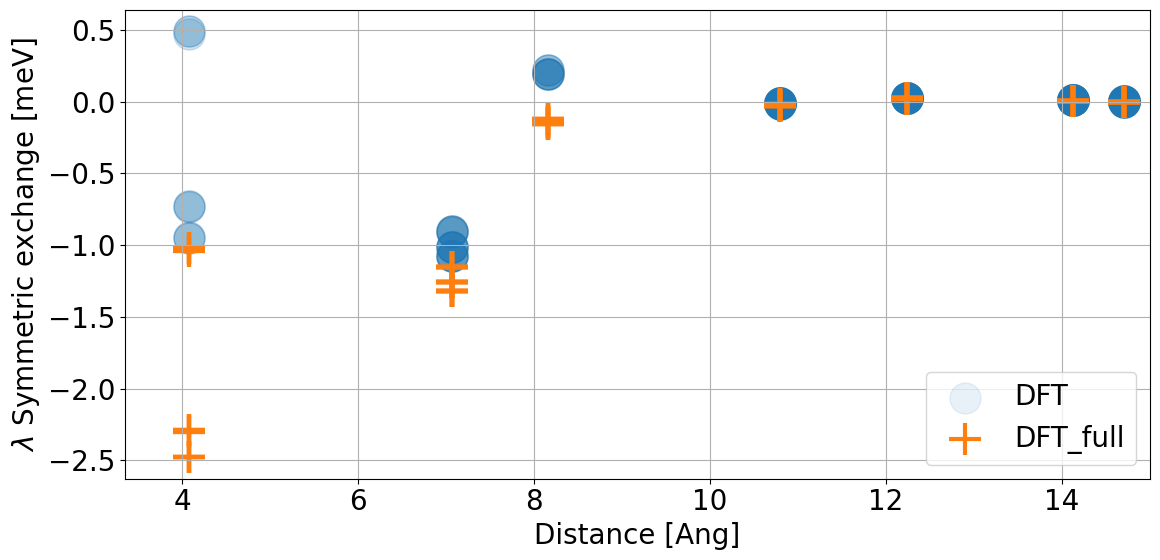
Experiment: Huang et al. Nature 546,270 (2017): 45K
CrI\(_3\) Monte-Carlo simulation
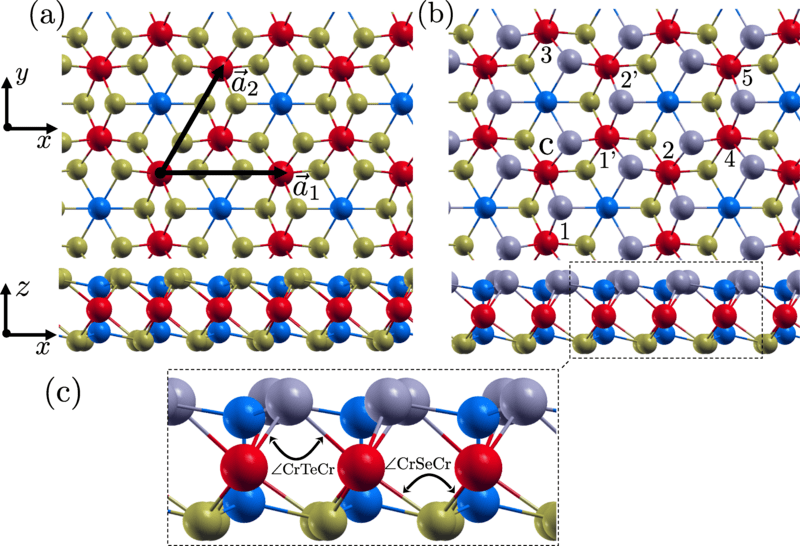
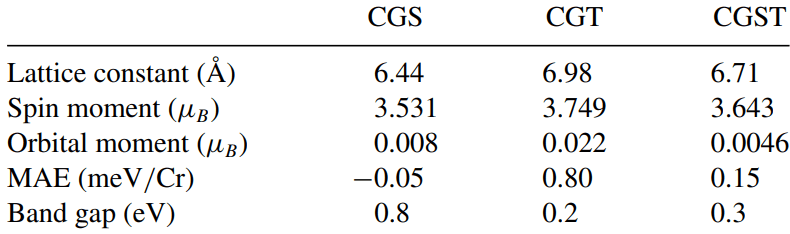
CrGeX\(_3\) (X = Se,Te) and Janus Cr\(_2\)Ge\(_2\)(Se,Te)\(_3\) monolayers
Phys. Rev. B 110, 184406 (2024)
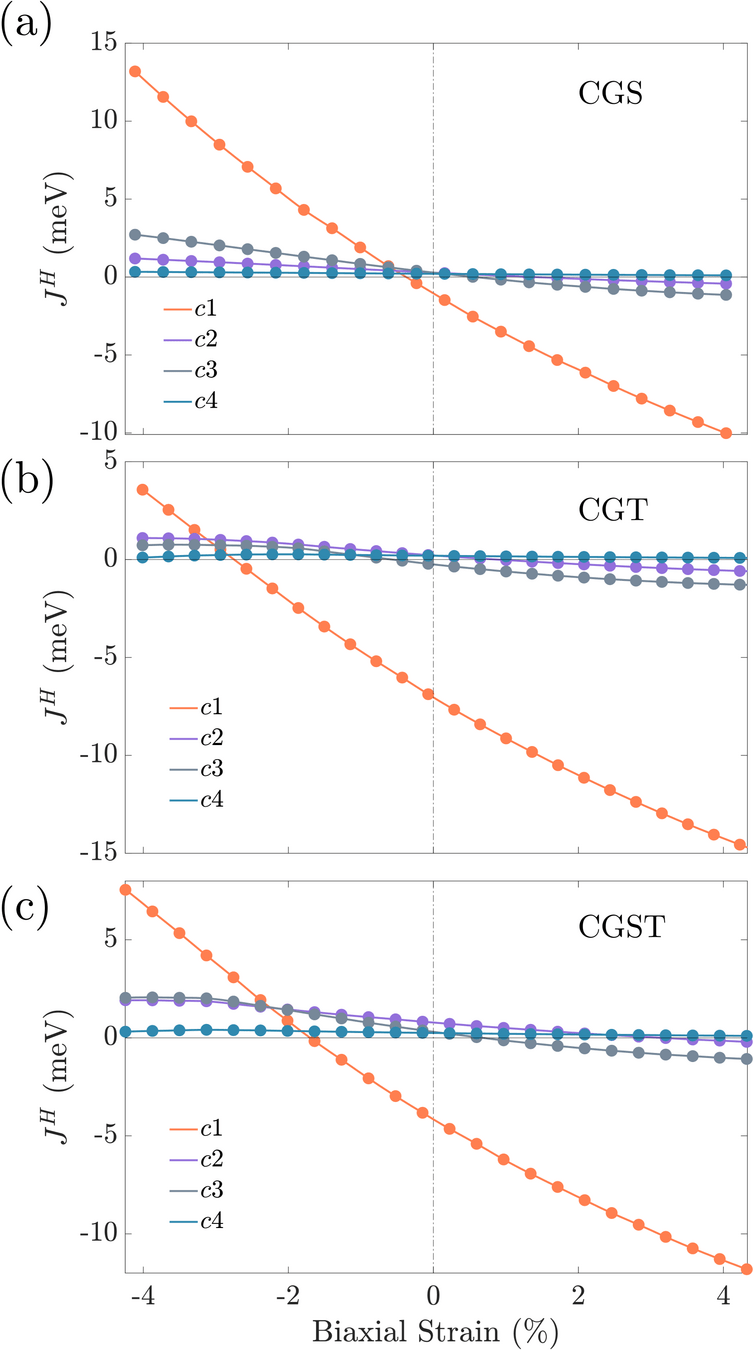




[meV]
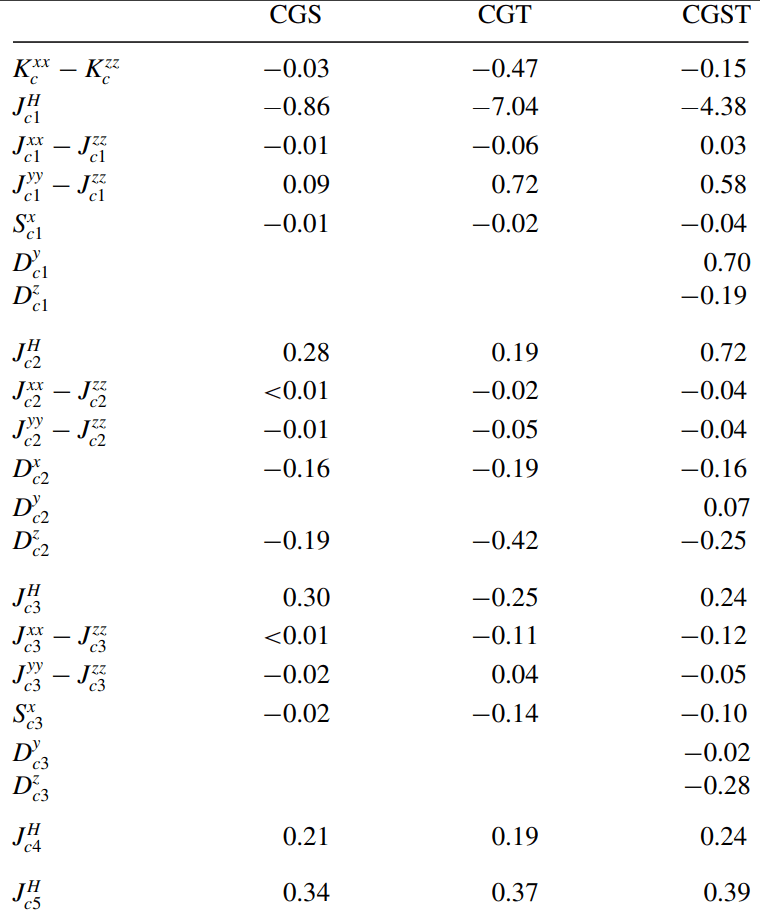
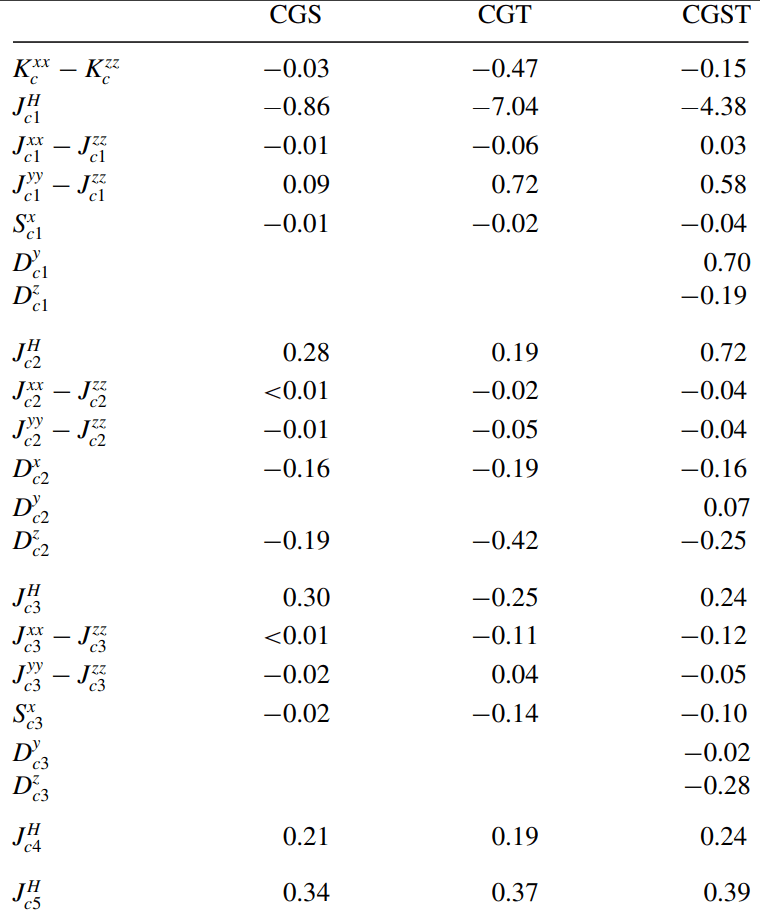
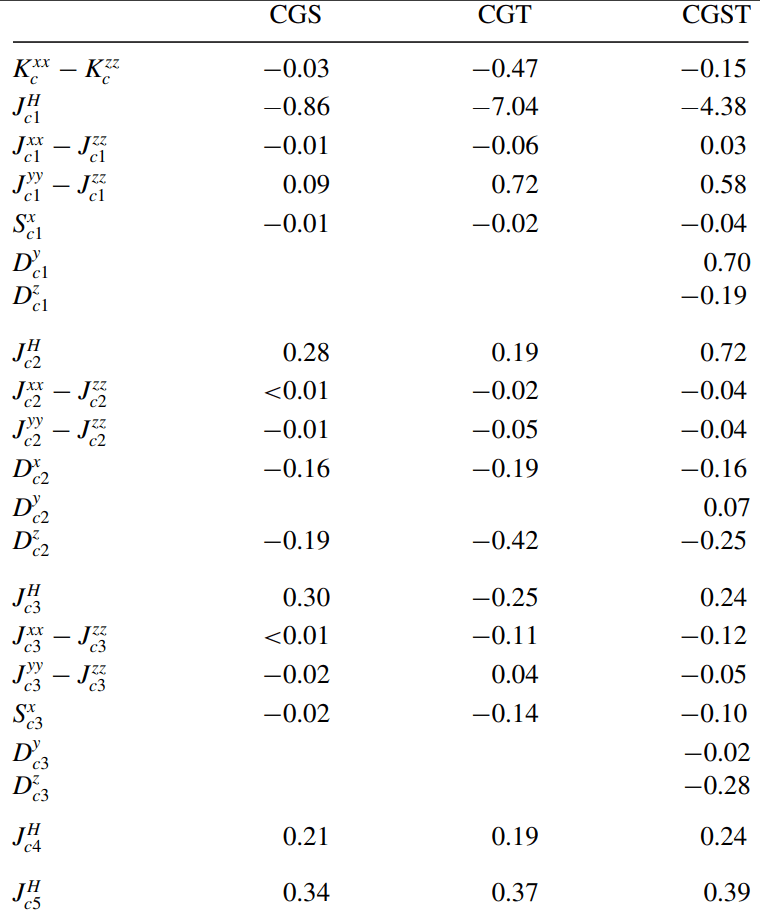
CrGeX\(_3\) (X = Se,Te) and Janus Cr\(_2\)Ge\(_2\)(Se,Te)\(_3\) monolayers

Phys. Rev. B 110, 184406 (2024)

Beyond two spin interaction: triangulene chains as S=1 Haldane chain
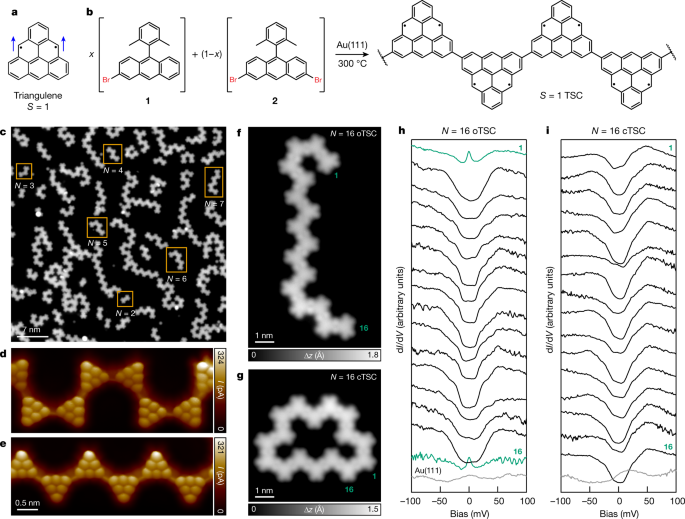
Mishra et al. Nature 598, 287 (2021).
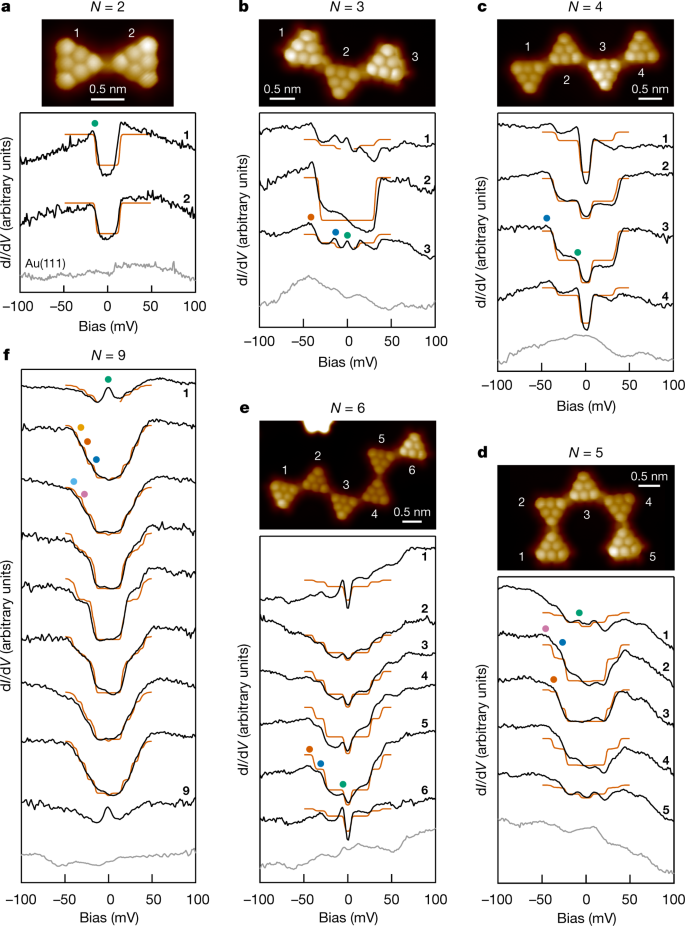
fit to BL-BQ model:
Bilinear-biquadratic exchange
| Dimer | Infinite chain | Experiment | |
|---|---|---|---|
| 17.7 meV | 19.75 meV | 18 meV | |
| 0.03 | 0.05 | 0.09 |
\( \beta \)
\( J \)
|
Martínez-Carracedo, Oroszlány, García-Fuente, Szunyogh, Ferrer Phys. Rev. B 107, 035432 (2023) |


Mishra et al.
Nature 598, 287 (2021).
FM and AFM reference is needed!
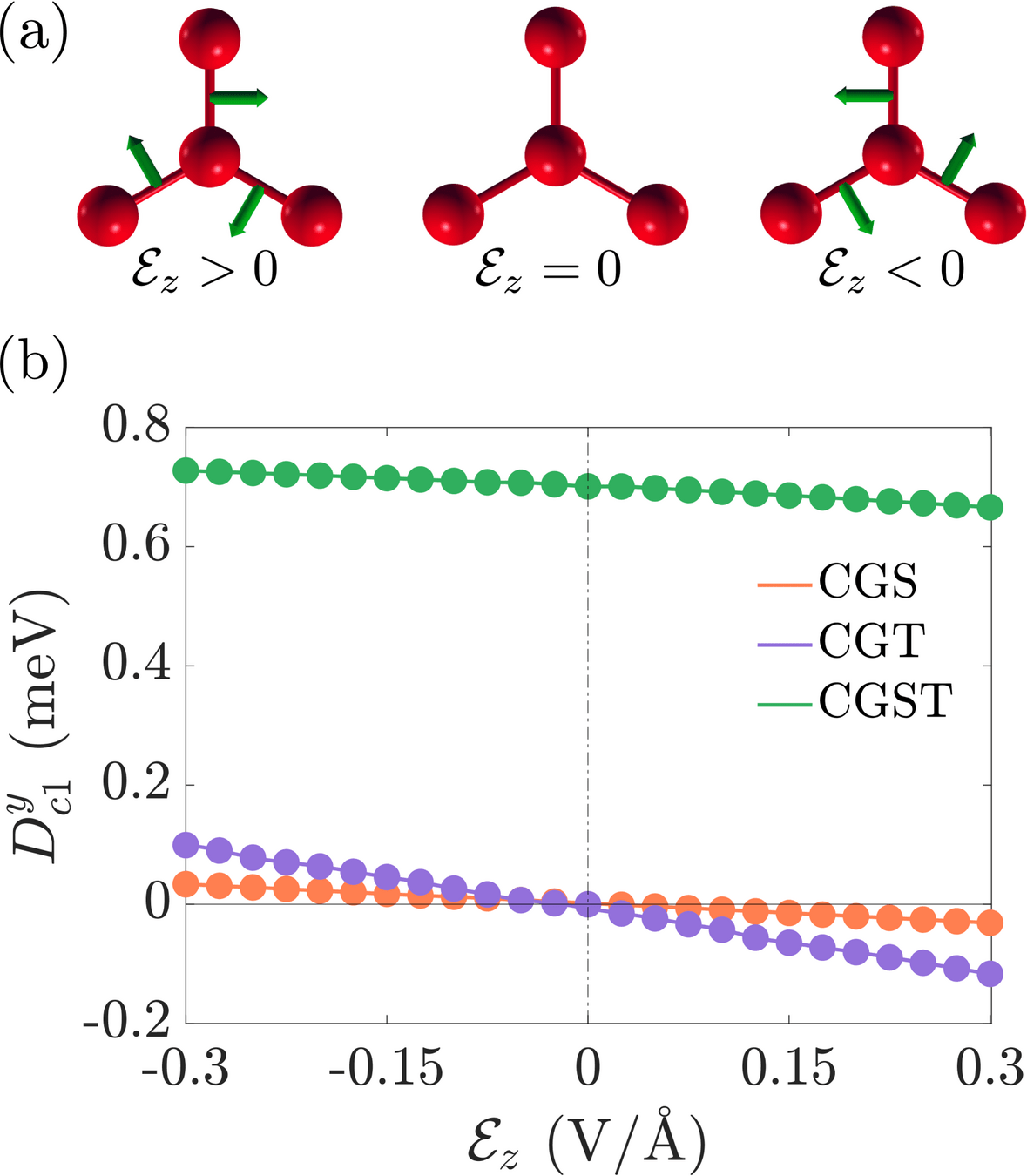
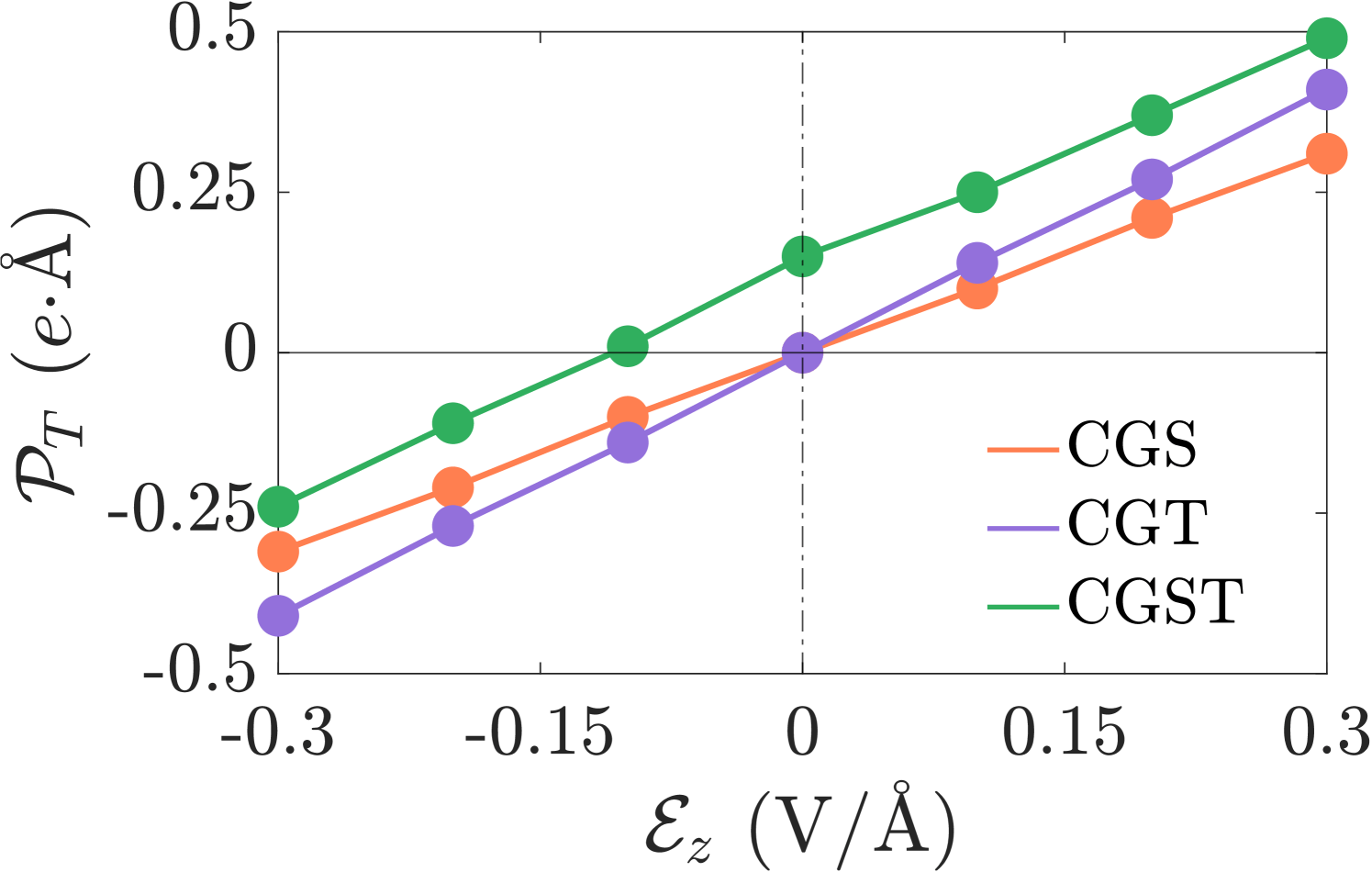
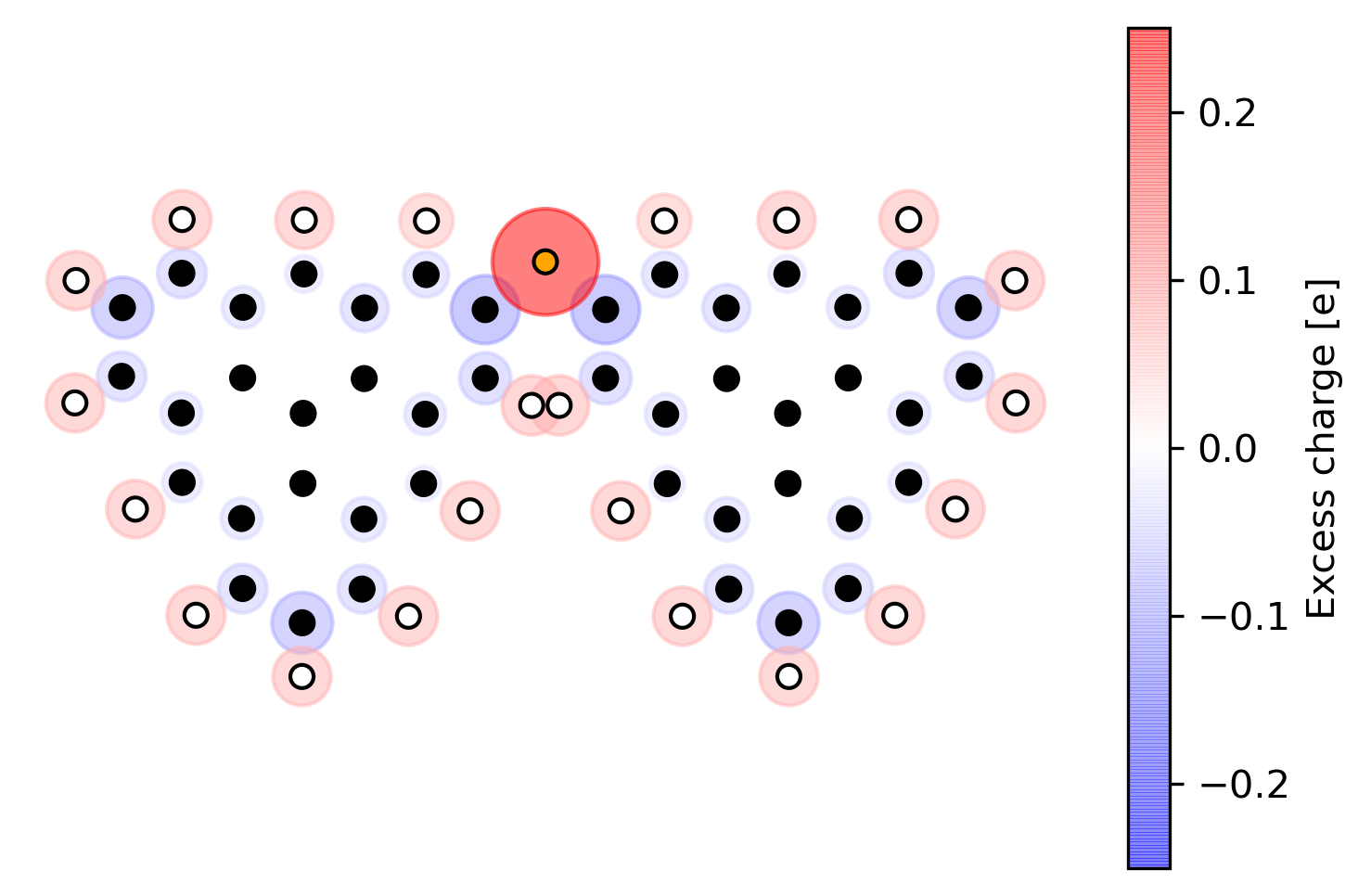
joining through S \(\Rightarrow\) dipole
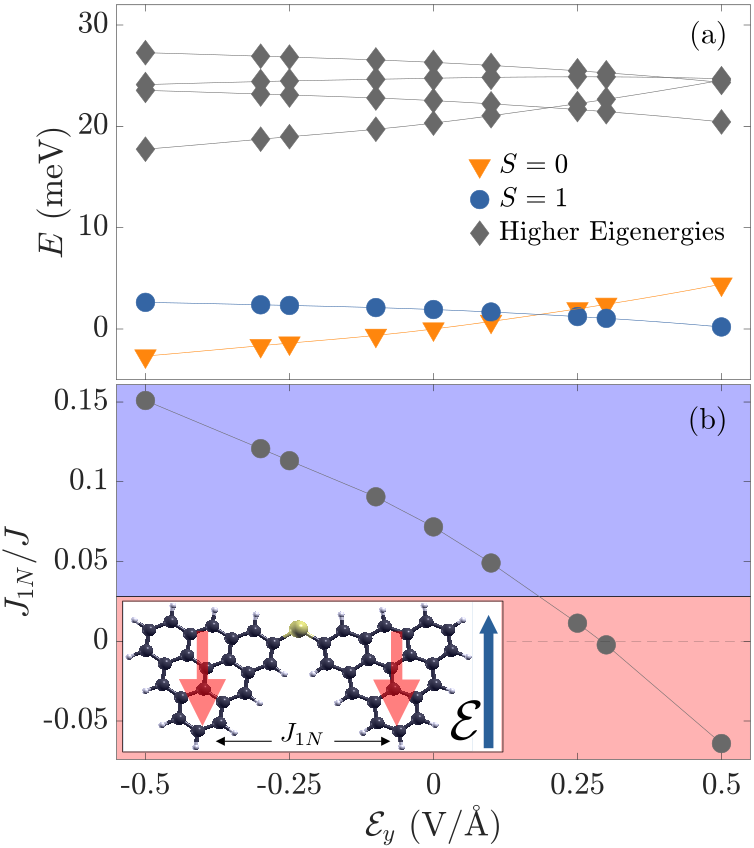
Singlet-Triplet transition through electric field



Get Grogu(py)!
- Very early release !!
- https://github.com/danielpozsar/grogu
- post. proc. for single DFT calculation
- parallel BZ integral with MPI or CUDA
- Generalised Heisenberg model

Number of orbitals: 8276
UNDER 1 Hour on 8 GPUs
pip install grogupy