Observation of competing, correlated ground states in the flat band of rhombohedral graphite
Department of Physics of Complex Systems, Eötvös Loránd University
MTA-BME Lendület Topology and Correlation Research Group, Budapest University of Technology and Economics



László Oroszlány








https://arxiv.org/abs/2201.10844
accepted in Science Advances
The Team
Theory
- Imre Hagymási, Dresden
- Zoltán Tajkov, CER
- János Koltai, ELTE
- Assem Alassaf, ELTE
- Péter Vancsó, CER
Experiment
- Mohammad Syahid Mohd Isa, CER
- Krisztián Márity, CER
- Péter Kun, Konrád Kandrai, CER
- András Pálinkás, CER
- Levente Tapasztó, CER
- Péter Nemes-Incze, CER


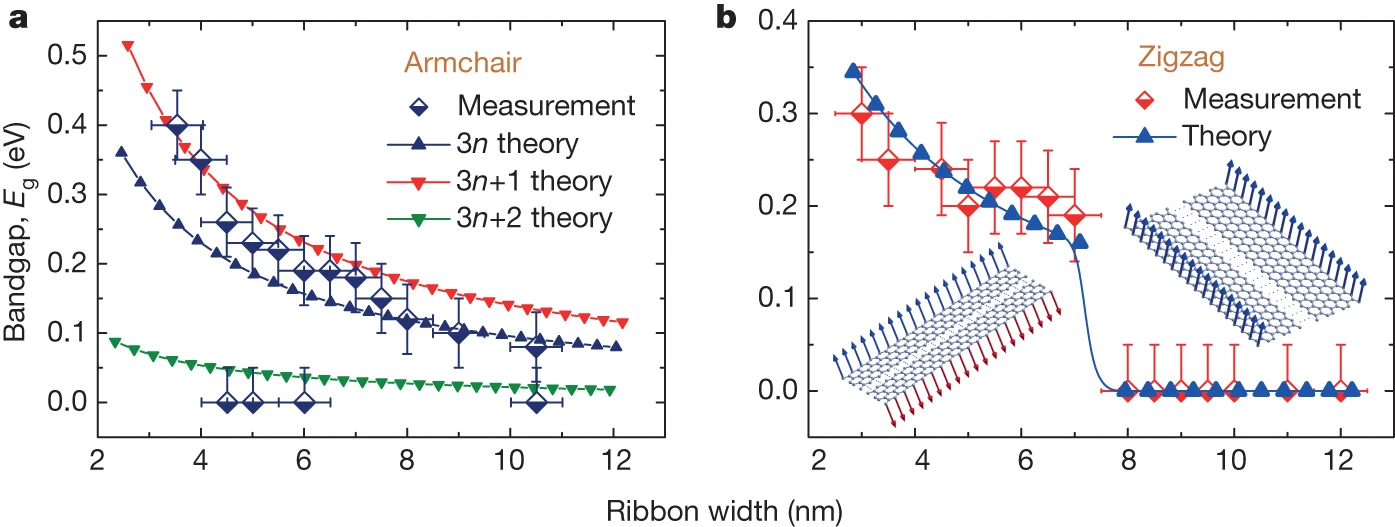
Magnetism at the edge of graphene ribbons
Magda et al. Nature 514, 608 (2014)

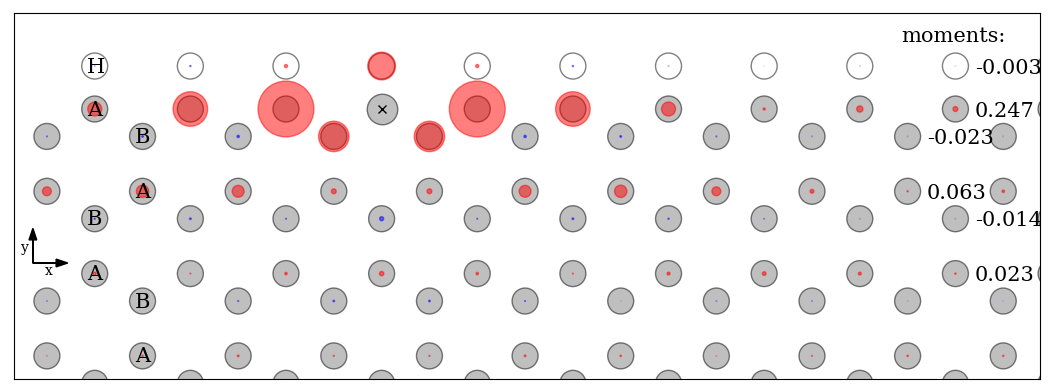
Ab initio calculations for edge magnetism
LO, J. Ferrer, A. Deák, L. Udvardi, L. Szunyogh, Phys. Rev. B 99, 224412 (2019)
Flat bands in magic angle graphene

Yuan Cao et al. Nature 556 43 (2018)





SSH chain
Rhombohedral (ABC) graphite
Sample preparation

Directed exfoliation:
5% \(\rightarrow\) 12% RG
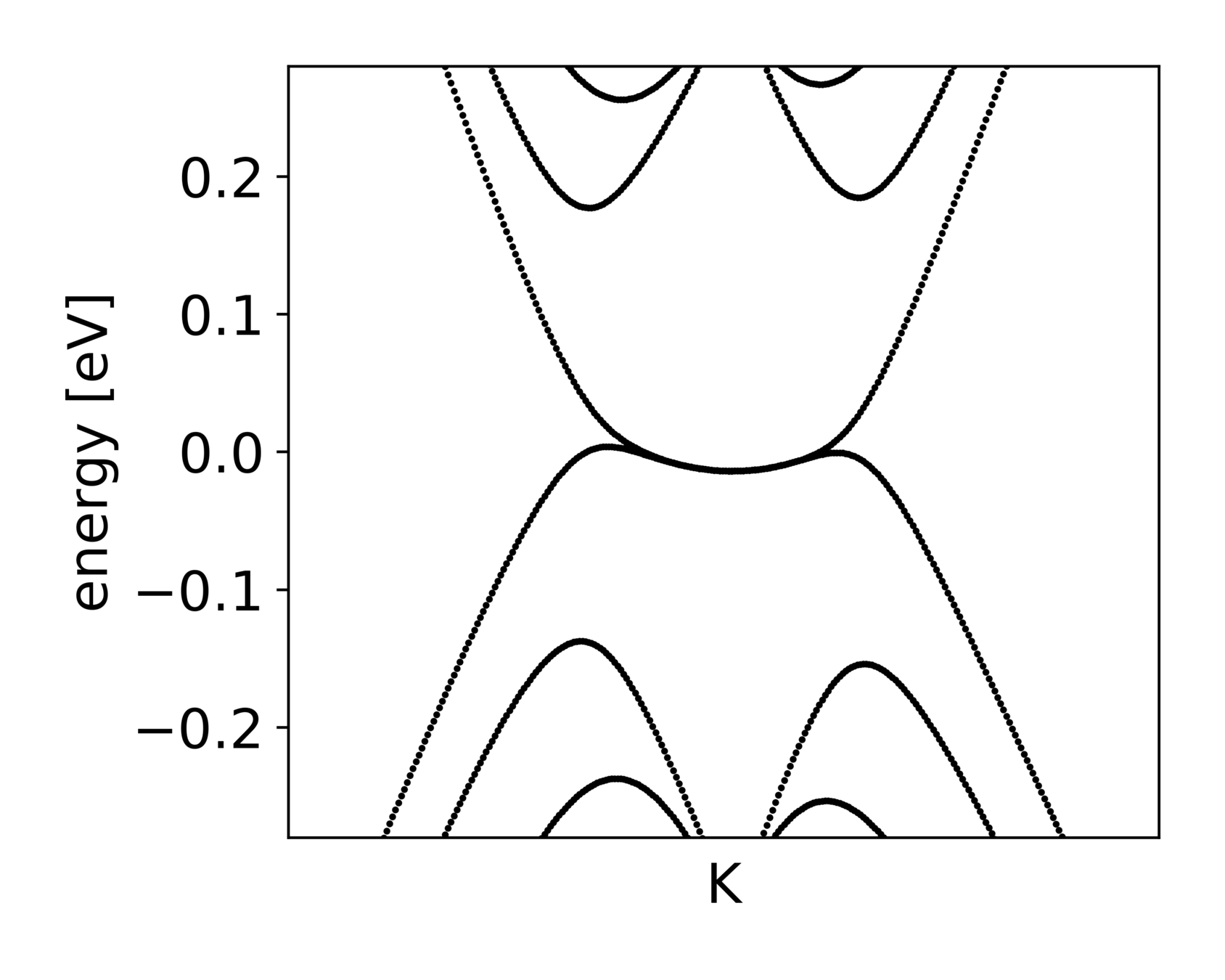
STM measurements: a broad overview

LDOS
LDA+U
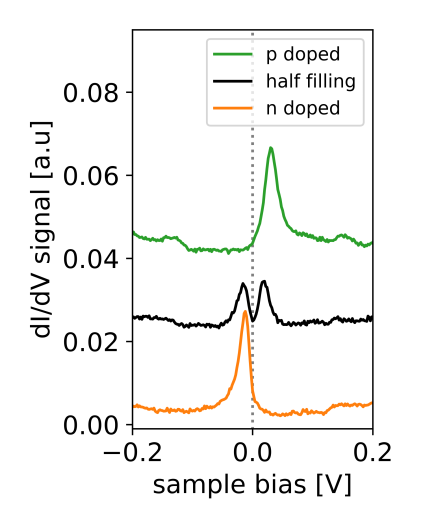
STM measurements: widths and splitts

Rising the temperature

\(T_c\)~15-20K


Splitting at half filling: strong perpendicular field
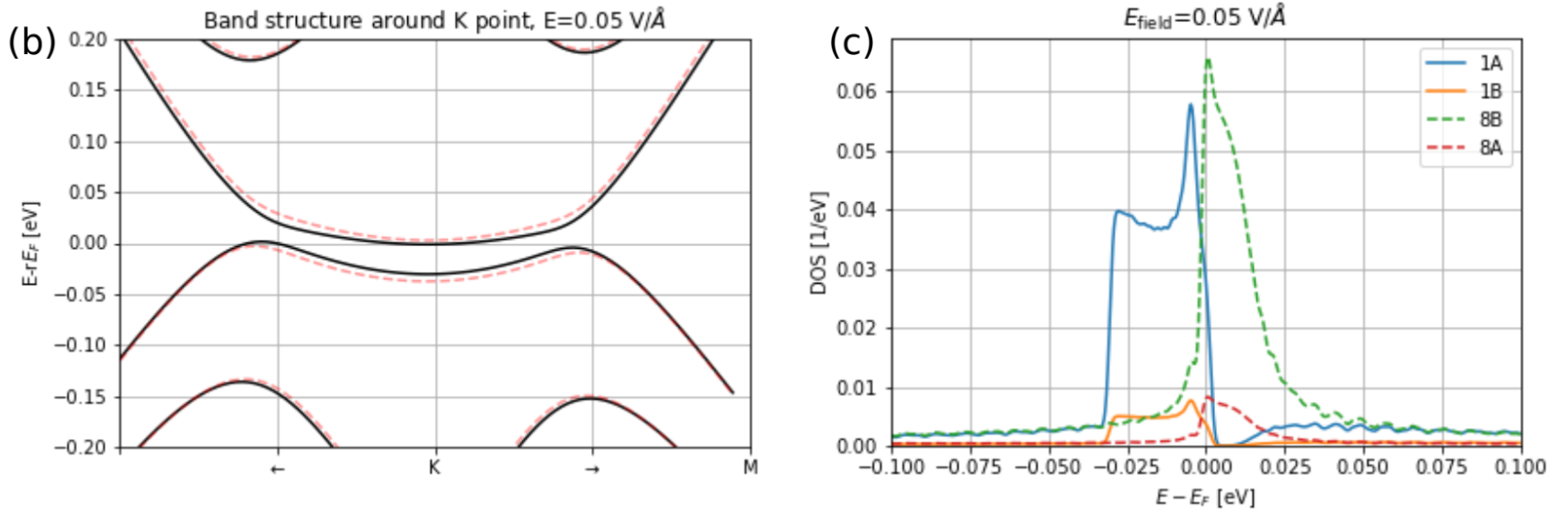
E-field strength 0.05 V/Å
TO BIG

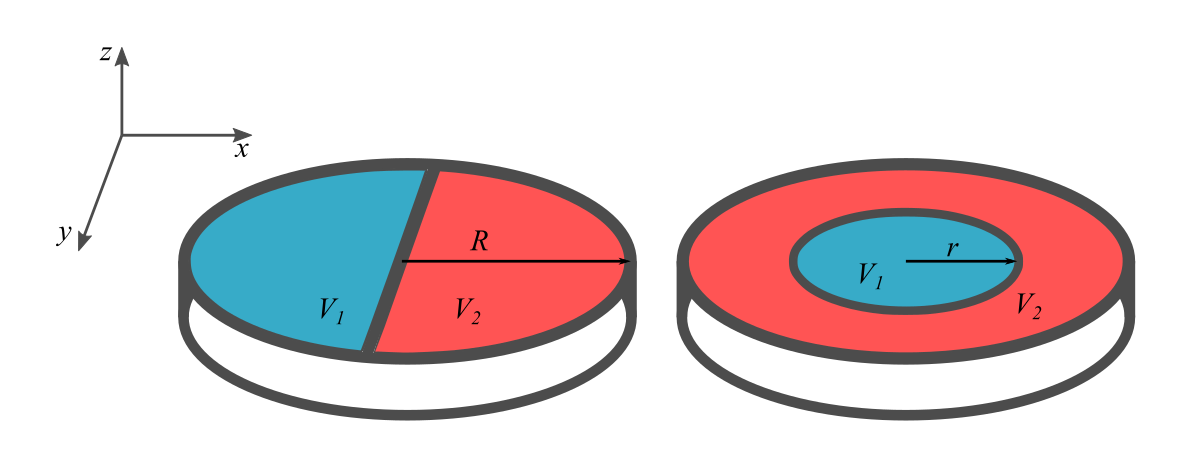
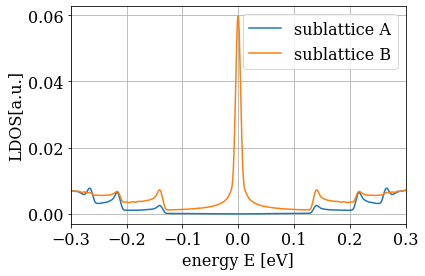
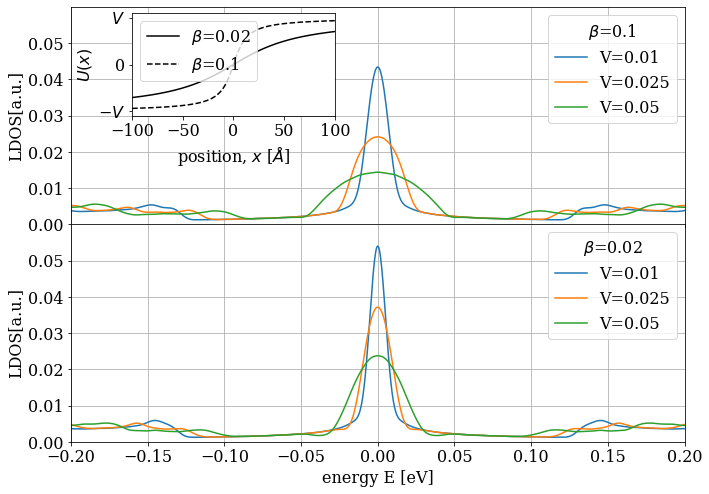
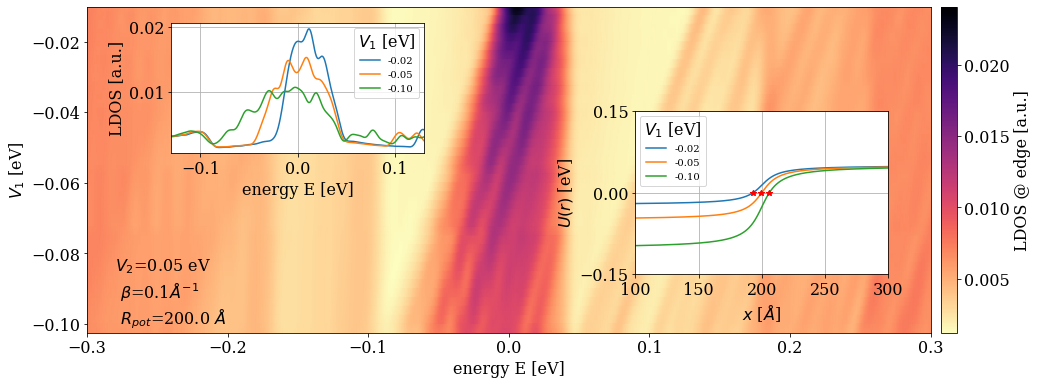
Splitting at half filling: confinement effects
SPLITTING PERSISTS BEYOND HALF FILLING!

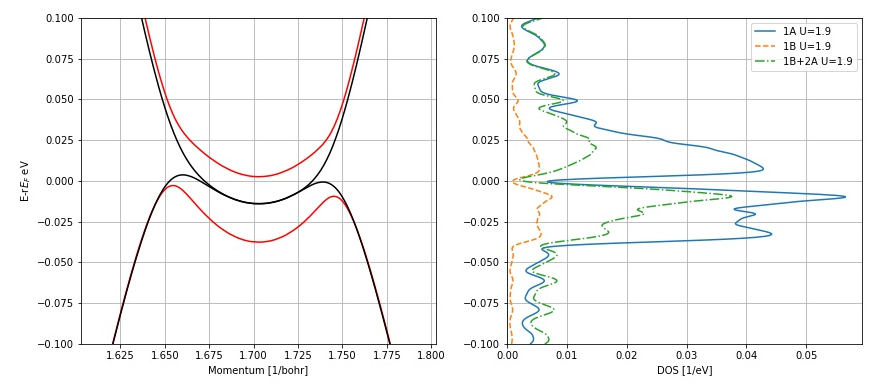
\( \mu_1 \approx 10^{-2} \mu_\mathrm{Bohr} \)
Splitting at half filling: mean-field physics
- LDA
- LDA+U
SPLITTING IS ALWAYS PRESENT AT HALF FILLING!
DMRG bootcamp

S. R. White, Phys. Rev. Lett. 69, 2863 (1992)
U. Schollwoeck, Annals of Physics 326, 96 (2011)
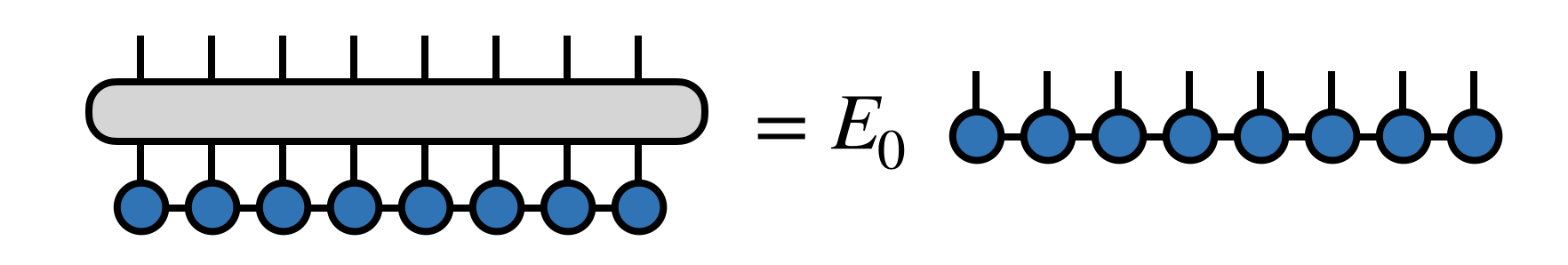
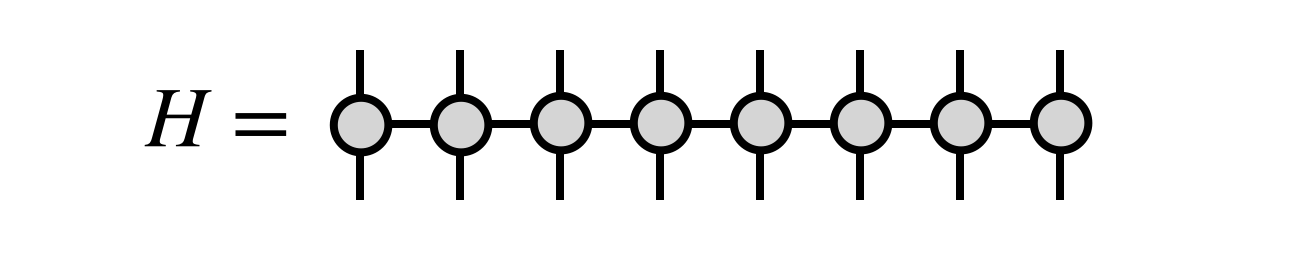
MPS Ansatz!
state of the art for 1D systems
higher dimensions are tricky
Results obtained with:
Budapest DMRG & ITensor codes
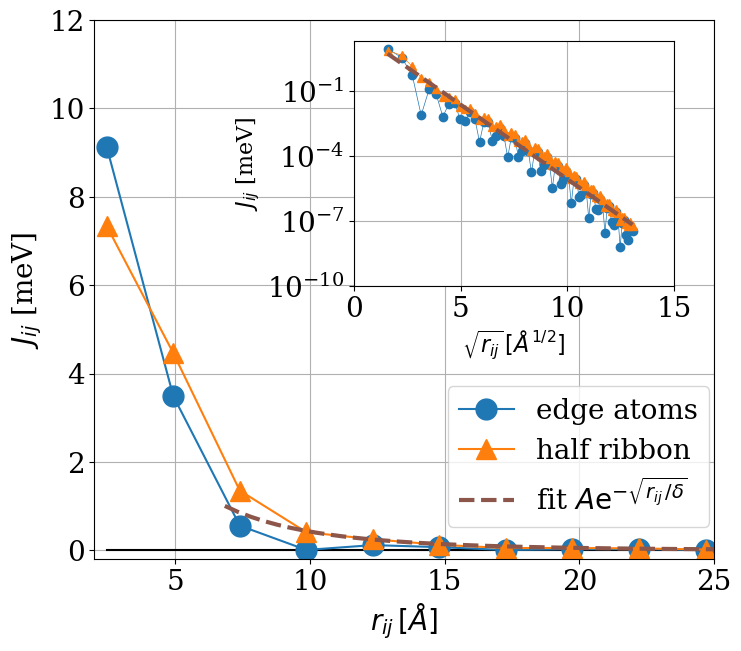
Interactions beyond meanfield

Three-fold degenerate groundstate!!
Competition of gaped and gapless states!
GAPED
GAPLESS
Symmetry breaking away from charge neutrality



Thank You for your attention!


