Flow Physics Explains Morphological Diversity of Ciliated Organs

Feng Ling

Nawroth Mechanobiology

Helmholtz Pioneer Campus

2023 APS March Meeting - PP08.08

Motile cilia are microscopic, hair-like cellular protrusions that direct fluid flow for almost all Eukaryotic life forms

Understanding how ciliated organ function has direct consequences on human health and diseases (airway, cerebral flow, reproduction, ...)

What is a ciliated organ?

Cilia manifest diverse motion despite their conserved structures

Cilia can coordinate in large numbers and organize in different spatial patterns for specialized flow functions

Roth, et al. (unpublished)

airway cilia

Larvacean funnel

Nawroth, Ling, et al.

20μm

Ciliated ducts that direct internal luminal flows are integral to animal physiology

Motile cilia are microscopic, hair-like cellular protrusions that direct fluid flow for almost all Eukaryotic life forms

Understanding how ciliated organ function has direct consequences on human health and diseases (airway, cerebral flow, reproduction, ...)

What is a ciliated organ?

Cilia manifest diverse motion despite their conserved structures

Cilia can coordinate in large numbers and organize in different spatial patterns for specialized flow functions

Roth, et al. (unpublished)

airway cilia

Larvacean funnel

Nawroth, Ling, et al.

20μm

Ciliated ducts that direct internal luminal flows are integral to animal physiology

Motile cilia are microscopic, hair-like cellular protrusions that direct fluid flow for almost all Eukaryotic life forms

Understanding how ciliated organ function has direct consequences on human health and diseases (airway, cerebral flow, reproduction, ...)

What is a ciliated organ?

Cilia manifest diverse motion despite their conserved structures

Cilia can coordinate in large numbers and organize in different spatial patterns for specialized flow functions

Roth, et al. (unpublished)

airway cilia

Larvacean funnel

Nawroth, Ling, et al.

20μm

Ciliated ducts that direct internal luminal flows are integral to animal physiology

Motile cilia are microscopic, hair-like cellular protrusions that direct fluid flow for almost all Eukaryotic life forms

Understanding how ciliated organ function has direct consequences on human health and diseases (airway, cerebral flow, reproduction, ...)

What is a ciliated organ?

Cilia manifest diverse motion despite their conserved structures

Cilia can coordinate in large numbers and organize in different spatial patterns for specialized flow functions

Roth, et al. (unpublished)

airway cilia

Larvacean funnel

Nawroth, Ling, et al.

20μm

Ciliated ducts that direct internal luminal flows are integral to animal physiology

Motile cilia are microscopic, hair-like cellular protrusions that direct fluid flow for almost all Eukaryotic life forms

Understanding how ciliated organ function has direct consequences on human health and diseases (airway, cerebral flow, reproduction, ...)

What is a ciliated organ?

Cilia manifest diverse motion despite their conserved structures

Cilia can coordinate in large numbers and organize in different spatial patterns for specialized flow functions

Roth, et al. (unpublished)

airway cilia

Larvacean funnel

Nawroth, Ling, et al.

20μm

Ciliated ducts that direct internal luminal flows are integral to animal physiology

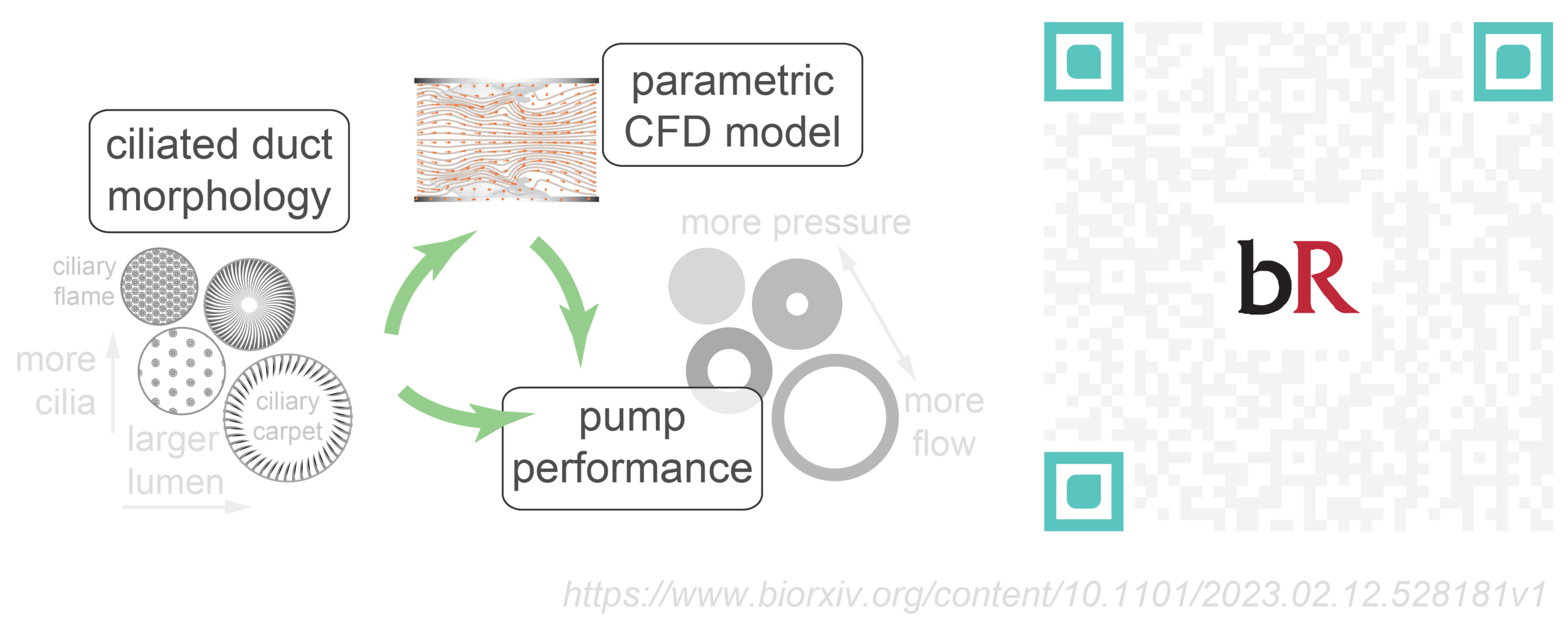
Ciliated ducts come in different ‘shapes’

Many animals have both "ciliary carpets," where short cilia grow perpendicular to the duct lumen, and "ciliary flames," where bundles of long cilia fill the duct lumen longitudinally.
Are these morphological differences related to their function?

Ciliary Carpet

Ciliary Flames

Esophagus

Ciliated Funnel

Nawroth, Ling, et al (2023)

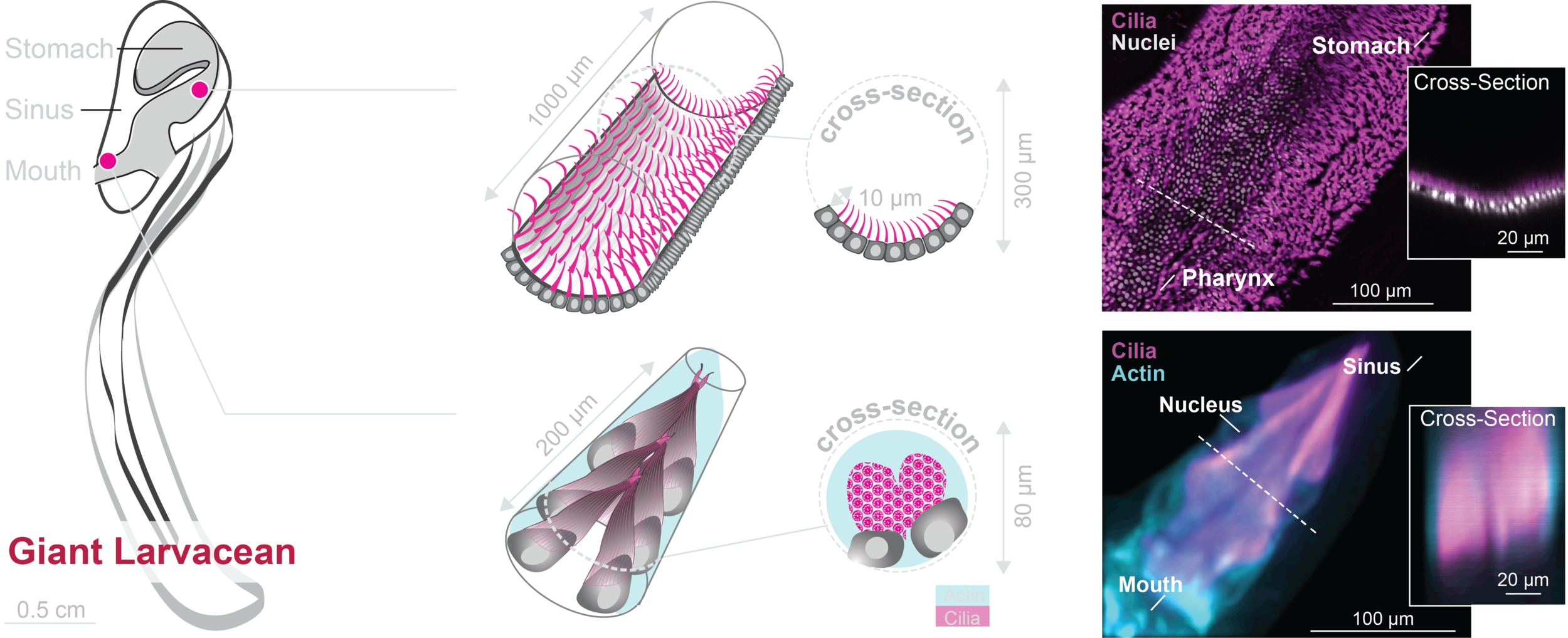
Curious case of the Giant Marine Larvacean

Ciliary Carpet

Ciliary Flames

Both types of ciliated ducts produce significant luminal fluid flow.
How can we probe the functional differences between these organs?

Nawroth, Ling, et al (2023)

Unified fluid model for all Ciliated Ducts

Cilia generate coordinated waves to drive luminal fluid flow.
We propose a quasi-1D duct model the can capture the essential flow physics for diverse duct morphologies AND enables the fair comparison of of their performance!

Nawroth, Ling, et al (2023)

Ciliary Carpet

Ciliary Flames

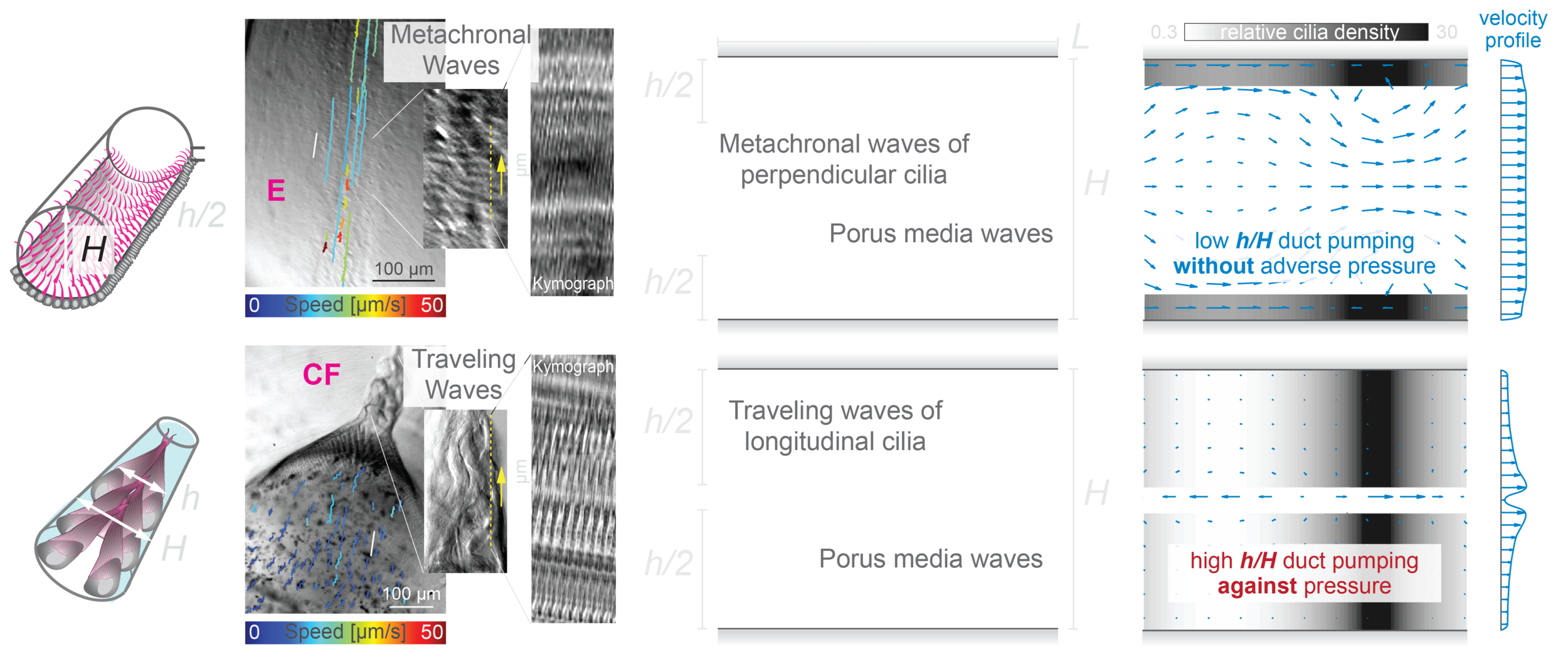
Motile cilia as Active porous media

Specifically, we model cilia activity as a porous media with prescribed quasi-1D density wave that transfer ciliary waves to fluid motion via drag forces
- \(h/H\) - cilia-to-lumen ratio
- \(H/L\) - lumen diameter / ciliary wavelength
Remaining inputs to the model are reference density of cilia \(\bar\rho_c\) and the adverse pressure \(\Delta P\).

Nawroth, Ling, et al (2023)

Motile cilia as Active porous media

Cilia-to-lumen Ratio h/H

Lumen Diameter H [μm]

Nawroth, Ling, et al (2023)

We fix the total amount of input activity by constraining the total amount of active material present inside a channel by
- \((\bar\rho_cL)(h/2r_{pore})=\bar\rho_ch=\text{const.}\)
This implies that carpet-like designs will need to be more densely distributed to be comparable to flame-like designs with the SAME lumen diameter

Quasi-1D metachronal wave

Prescribing the 1D wave by setting

\(\bm{v}_c = \begin{cases} \bm{0} & y\in (h/2, H-h/2)\\ v_c(x,t) {\bm{e}}_x & \text{otherwise} \end{cases}\)

\(\zeta_c =\begin{cases} 0 & y \in (h/2, H-h/2)\\ \bar\zeta_c\left(\partial_x x_c(x,t)\right)^{-1} & \text{otherwise} \end{cases} \)

with \(\bar\zeta_c =\bar\rho_c\dfrac1{Lh}\dfrac{F_{drag}}{v_c}=3\pi\mu\bar\rho_c^2\), and

\(F_{drag}=(\bar\rho_cL)( h/{2r_{pore}})(6\pi\mu r_{pore}v_c)\)

Since \(x_c=x_c(kx-\omega t)\) is a traveling wave, only need to solve for \(\bm{u}\) at \(t=t_o\)

\(v_c(x,t)\)

\(x_c(x,t)\)

\(x_c(x,t) = x + \epsilon \cos(2\pi x/L+\omega t)\)

\(\langle v_c\rangle_x=\frac{1}{L}\int_0^L v_c(x,0)\,\mathrm{d} x=\pi \omega\epsilon^2/L\)

\(v_c(x_c,t) = \dfrac{\partial x_c}{\partial t}, \rho_c(x_c,t) = \bar\rho_c \left( \dfrac{\partial x_c}{\partial x} \right)^{-1}\)

Taylor (1951) & Blake (1971)

Pak, Lauga, Proc. R. S. A (2009)

Nawroth, Ling, et al. ???

Brinkman-Stokes equation

For simplicity, we only consider one-way coupling of cilia driven velocity as drag forces on to the fluid

Resulting equations are solved numerically via mixed FEM

\(p(0,y,t)=p(L,y,t)\)

\(\bm{u}(0,y,t)=\bm{u}(L,y,t)\)

\(\bm{u}(x,0,t)=\bm{u}(x,H,t)={0}\)

\(-\nabla^2 \bm{u} + \nabla p + \zeta_c(\bm{u}-\bm{v}_c) = \Delta p/L\cdot\bm e_x\)

\(\nabla \cdot \mathbf{u} = 0\)

Nawroth, Ling, et al. ???

\(\mu\)

\(\omega\)

\(L\)

\(\epsilon\)

\(h/H\)

\(H\)

\(\Delta P\)

\(\bar\rho_ch\)

\(U=\int_0^L\bm u\cdot\bm e_x\)

\(10^{-3}\) [Pa\(\cdot\)s]

\(15\sim30\) [Hz]

\(100\) [μm]

\(L/2\pi\)

\(0-1\)

\(5-200\times10^{-6}\) [m]

\(0-100\) \(Pa\)

\(1\sim1000\)

\(\leq \omega L /(4\pi)\)

fluid viscosity

wave frequency

imposed wavelength (wave number \(=1\))

wave amplitude \(\in(0,\lambda/2\pi)\)

cilia-to-lumen ratio

duct lumen diameter

adverse pressure gradient

material constraint constant

mean flow speed

Model parameters

Nawroth, Ling, et al. ???

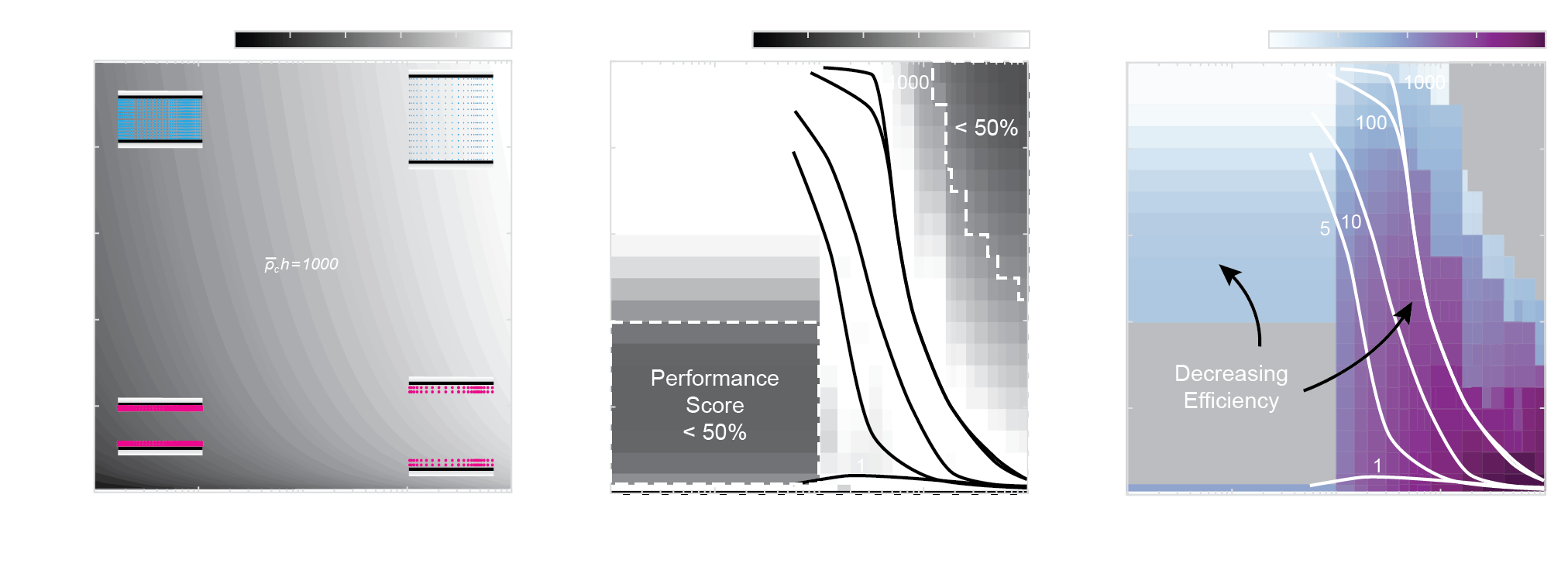
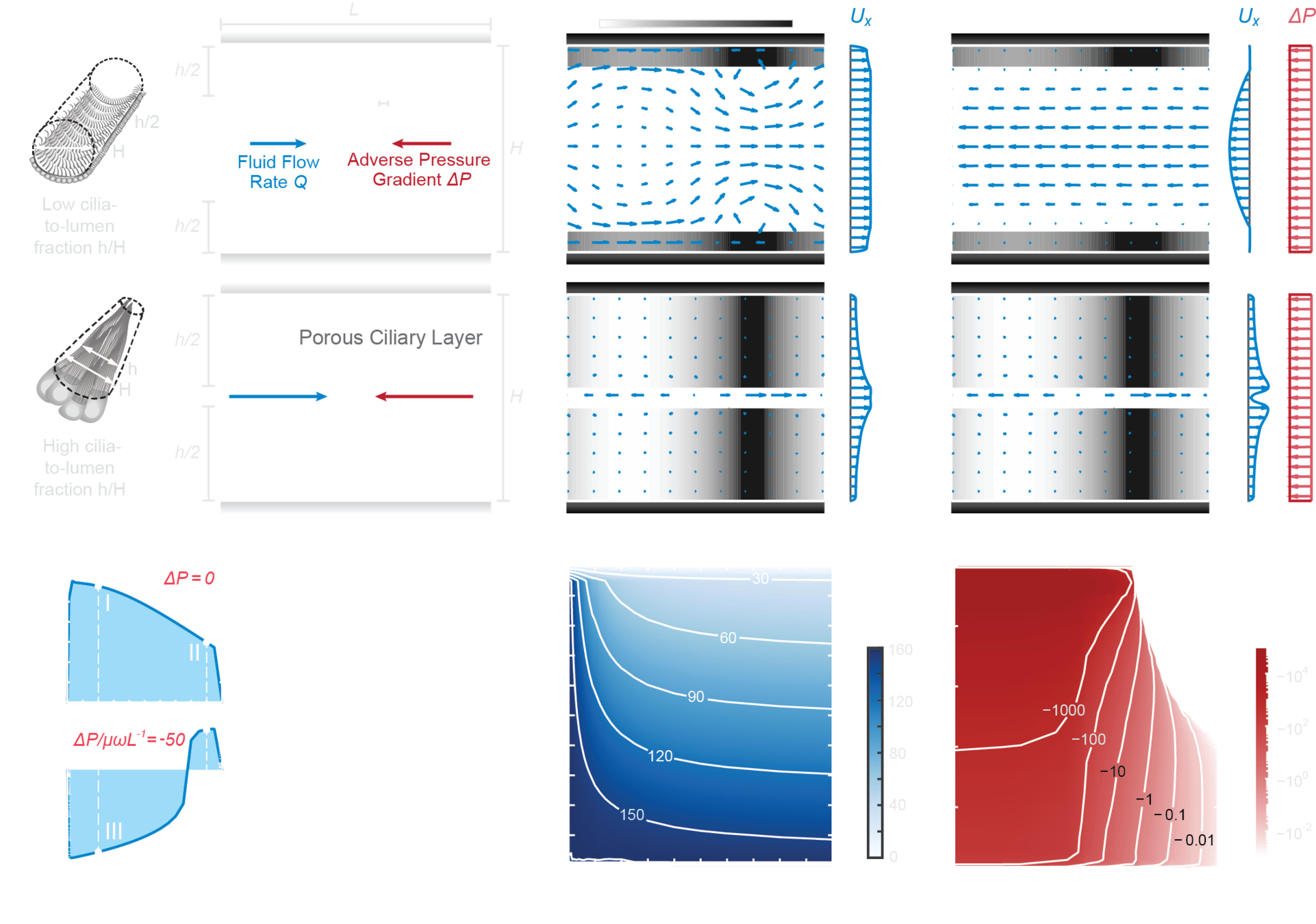
Ciliary carpet Maximizes flow rate

In absence of adverse pressure,

Low cilia-to-lumen ratio h/H and large lumen diameter H (ciliary carpet) produces the largest possible flux
In the limit of thin, dense layer of cilia, we recover the theoretical upper bound for flow as predicted by the classic envelope model of Black (1971)

Nawroth, Ling, et al (2023)

Ciliary carpet Maximizes flow rate

In stark contrast, even mild adverse pressure can reverse the net flow!

In absence of adverse pressure,

Low cilia-to-lumen ratio h/H and large lumen diameter H (ciliary carpet) produces the largest possible flux
In the limit of thin, dense layer of cilia, we recover the theoretical upper bound for flow predicted by the classic envelope model of Black (1971)

Nawroth, Ling, et al (2023)

Unless under Pressure

Ciliary flame pumps less fluid

In absence of adverse pressure,

High cilia-to-lumen ratio h/H and small lumen diameter H (ciliary flame) produces less flux than carpets
This is because the active ciliary layers also introduce material that adds resistance/restrictions to luminal flow

Nawroth, Ling, et al (2023)

Ciliary flame can Pump against Pressure

However, unlike the case of ciliary carpets, ciliary flames is much more robust against adverse pressure!

In absence of adverse pressure,

High cilia-to-lumen ratio h/H and small lumen diameter H (ciliary flame) produces less flux than carpets
This is because the active ciliary layers also introduce material that adds resistance/restrictions to luminal flow

Nawroth, Ling, et al (2023)

Pressure-Flow tradeoff for ciliary pumps

Just like any engineered pumps, ciliated duct with fixed morphology is most efficient (maximum \(\eta\)) when pumping at the 'shoulder' of their operating curve (solid lines)
- \(\eta=\dfrac{\text{power transmitted to fluid}}{\text{power input by cilia}}\propto\dfrac{QU^2}{\bar\rho_ch}\)
Ducts with smaller \(H\) and higher \(h/H\) can pump against larger pressure without compromising efficiency
This suggests \(h/H\) and \(H\) should be inversely related if natural ducts are flow efficient!

\(\mu\) - viscosity; \(\omega\) - cilia beat frequency; \(L\) - ciliary wavelength

Nawroth, Ling, et al (2023)

Just like any engineered pumps, ciliated duct with fixed morphology is most efficient (maximum \(\eta\)) when pumping at the 'shoulder' of their operating curve (solid lines)
- \(\eta=\dfrac{\text{power transmitted to fluid}}{\text{power input by cilia}}\propto\dfrac{QU^2}{\bar\rho_ch}\)
Ducts with smaller \(H\) and higher \(h/H\) can pump against larger pressure without compromising efficiency
This suggests \(h/H\) and \(H\) should be inversely related if natural ducts are flow efficient!

\(\mu\) - viscosity; \(\omega\) - cilia beat frequency; \(L\) - ciliary wavelength

Nawroth, Ling, et al (2023)

Pressure-Flow tradeoff for ciliary pumps

Just like any engineered pumps, ciliated duct with fixed morphology is most efficient (maximum \(\eta\)) when pumping at the 'shoulder' of their operating curve (solid lines)
- \(\eta=\dfrac{\text{power transmitted to fluid}}{\text{power input by cilia}}\propto\dfrac{QU^2}{\bar\rho_ch}\)
Ducts with smaller \(H\) and higher \(h/H\) can pump against larger pressure without compromising efficiency
This suggests \(h/H\) and \(H\) should be inversely related if natural ducts are flow efficient!

\(\mu\) - viscosity; \(\omega\) - cilia beat frequency; \(L\) - ciliary wavelength

Nawroth, Ling, et al (2023)

Pressure-Flow tradeoff for ciliary pumps

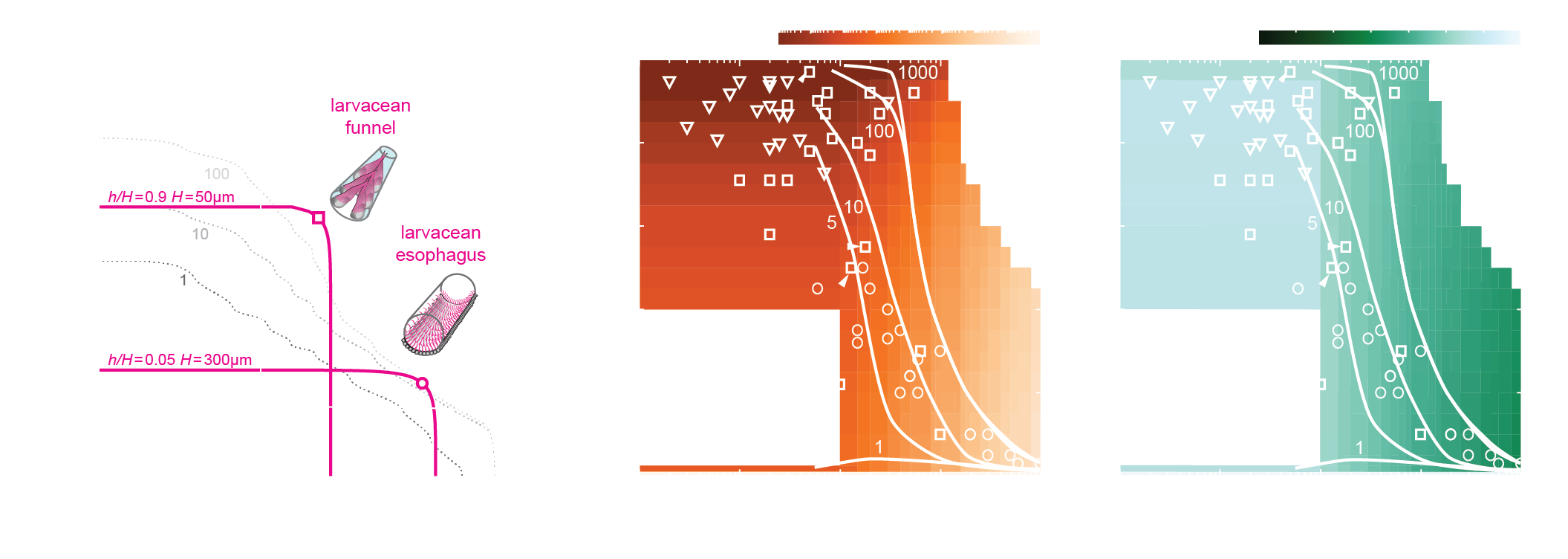
Morphometric spectrum of ciliated ducts

Cilia-to-lumen Ratio h/H

Lumen Diameter H [μm]

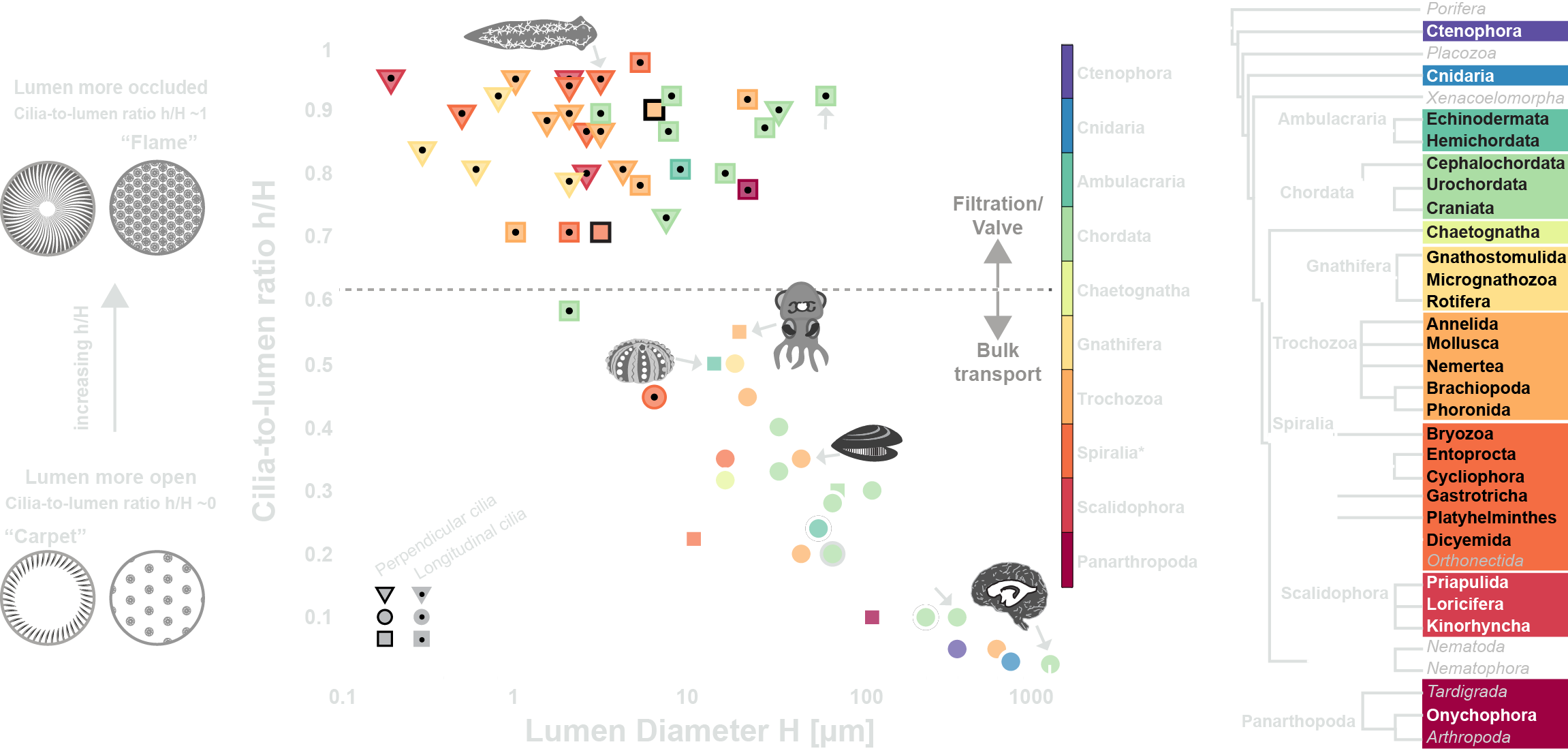
Survey of 58 ducts from 26 phyla neatly reveals an inverse relationship between \(h/H\) and \(H\)!
Where available, our data also show flow function correlates with the value of \(h/H\)!
Can our model explain this correlation?
Why aren't there ducts at the anti-diagonal corners?

more open space in the duct

less open space in the duct

Nawroth, Ling, et al (2023)

airway

tissue

Universal design rules for ciliary pumps

Convergence of ciliated duct designs follows functional and efficiency constraints rather than phylogenetic distance!

high \(h/H\) small \(H\) \(\rightarrow\) better for pressure generation (filtration/valve)
low \(h/H\) large \(H\) \(\rightarrow\) better for flux generation (bulk transport)
a continuous design spectrum emerges in accordance with the biological data.