Proximal-to-distal Molecular Motor Asymmetry Controls Flagellar Wave Reversal
[U02.10]
Feng Ling, Yi Man, Eva Kanso
University of Southern California
APS DFD 2020


Tap me!
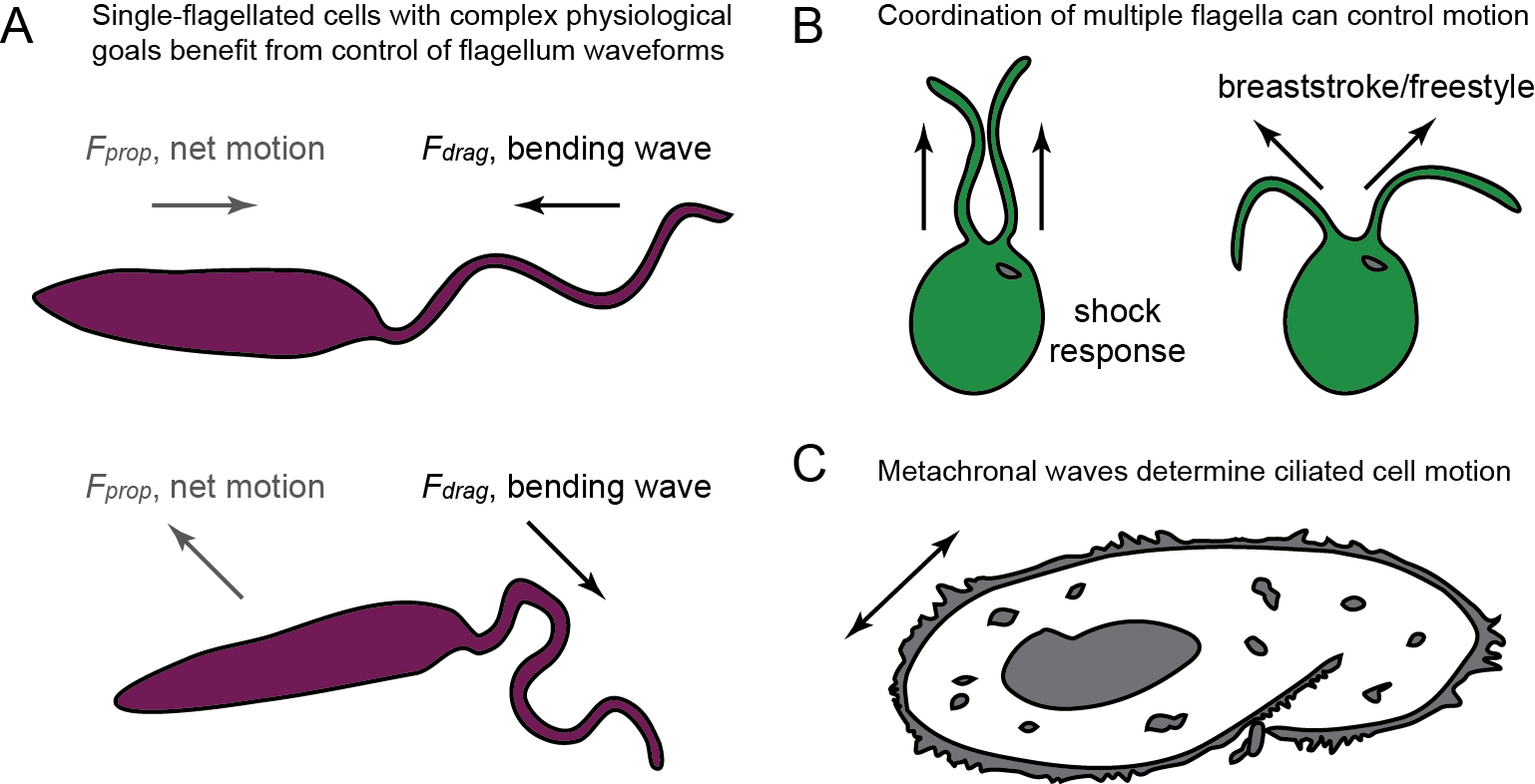
What is flagellar wave reversal?
Quick turn around
Rapid braking
Journey to the Microcosmos (2020)
But why wave reversals?
-
a common navigation strategy is to intersperse a "running/forward" gait with bursts of "tumble/reverse/stop" phase where sensing could occur
-
this means mono-flagellates need flagellar wave reversals
-
two model organisms exhibiting wave reversal traits are parasites that separately cause sleeping sickness and Leishmaniasis.


Tip-to-base (T2B) "forward" waves
Base-to-tip (B2T) "reversed" waves
Euglenozoa
Kinetoplastida
Trypanosomatida
T. Brucei
L. Mexicana
Diversity for Complex Function



metachronal waves
Not all flagellar waves reverse
-
spermatozoa typically swim with base-to-tip (B2T) waves in helical trajectories
-
multi-flagellated cells and ciliated microorganisms can change locomotion strategies by altering cilia/flagella synchronization
Lin and Nicastro (2018)

Lin and Nicastro (2018)
Diversity from Similar Structures
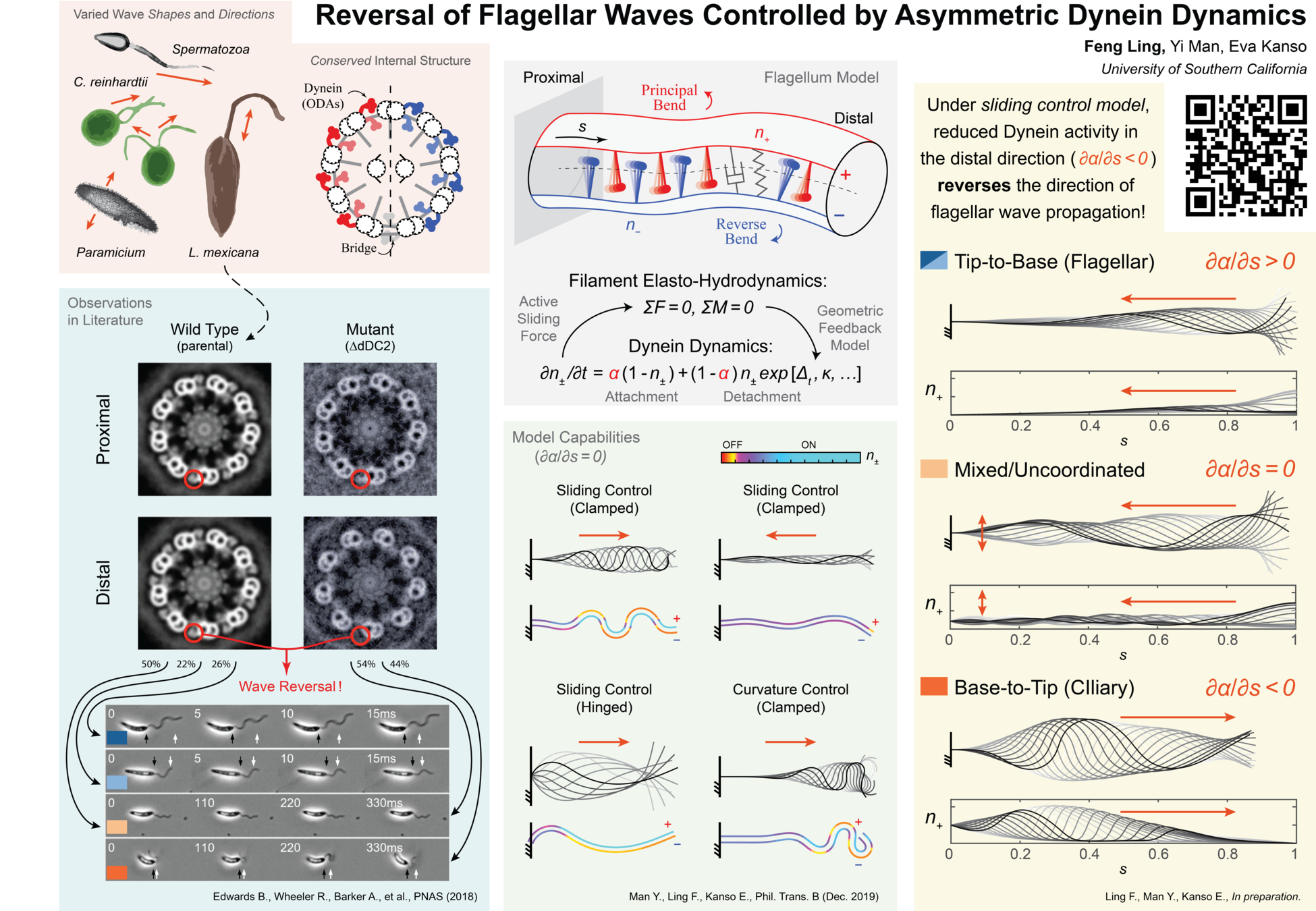
How do homologous internal structures and mechanisms produce this diversity in motion?
How does the length-wise symmetric axoneme produce waves that travel in different directions?
Less Tip motors => less T2B waves
-
experiments on genetic mutants link wave reversal to asymmetry in dynein motors
-
specifically, wild type organism typically exhibit tip-to-base (T2B) waves, while mutants missing dynein arms near the tip favor base-to-tip (B2T) waves*
-
can/do wild type organisms use this asymmetry to control wave direction?
Edwards et al., PNAS (2018)
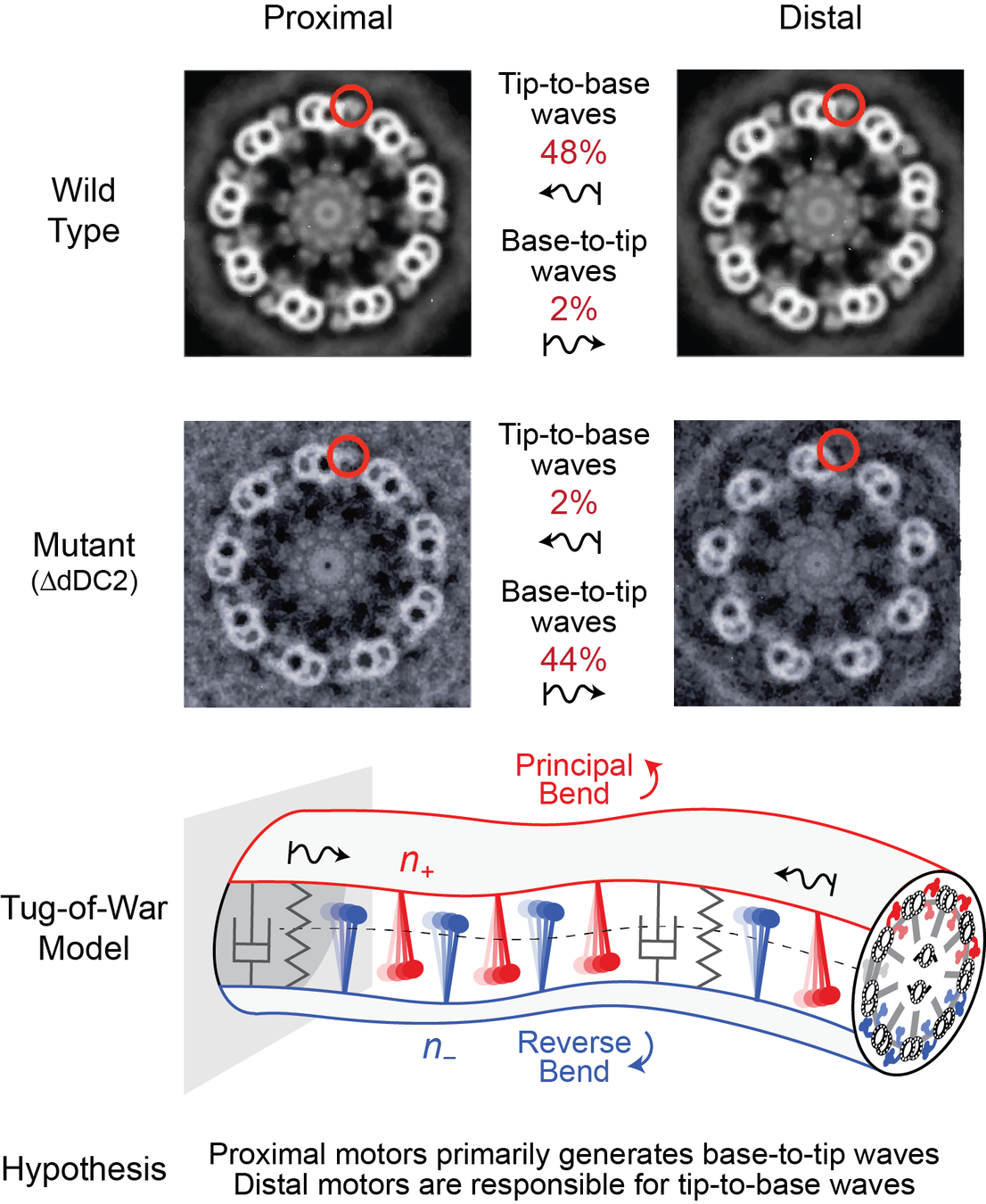
Wild Type Statistics /
Tip-to-Base
Mixed/Static
Base-to-Tip
Intermittent T2B
26%
22%
50%
2%
Mutant Statistics
1%
1%
54%
44%
Observed Waveforms
Tap Me !
Edwards et al., PNAS (2018)
Tug-of-War Model of Flagellum

-
model a flagellum as two micro-filaments coupled elastically and via molecular motor dynamics*
-
each filament (\(\,+\) and \(−\) ) has a population of motors that bend the centerline in opposite directions (\(\,n_+\) and \(n_-\))
-
Motors attach under a fixed rate but detach due to both natural transitions & geometric feedback

Motor Dynamics & Geometric Feedback
-
binding/unbinding (attach/detach) of dynein \(\rightarrow\) inter-doublet sliding
-
sliding force couple + elastic resistance \(\rightarrow\) active bending moment
-
feedback could arise via sliding control, curvature control, or "geometric clutch"
Qiu et al., Nature Struct. Mol. Bio (2012)

Sartori et al., eLife (2016)
Dimensional & Dimensionless Parameters
flagellum length
diameter
bending rigidity
drag coefficient
\(L~~~~~~~~~~~\sim50\,[\mu m]\)
\(d~~~~~~~~~~\sim200\,[nm]\)
\(B~~~~~~\sim1\,[nN\,\mu m^2]\)
\(\xi_\perp~~~~ 10^{-3}\sim1\,[Pa\,s]\)
doublet link modulus
total dynein density
\(K~~~~\sim 2\,[\mu N\,\mu m^{-2}]\)
\(\rho~~~~~~~~\lesssim 400\,[\mu m^{-1}]\)
dynein stall force
detachment force
null-force speed
reaction time
\(f_o~~~~~~~~~~~~1\sim5\,[pN]\)
\(f_c~~~~~~0.5\sim2.5\,[pN]\)
\(v_o~~~~~~~5\sim7\,[\mu m\,s^{-1}]\)
\(\tau_o~~~~~~~~~~~\sim50\,[ms]\)
sperm number
\(\text{Sp}^4\;=~\dfrac{\xi_\perp L/\tau_o}{B/L^3}\)
passive moment
duty ratio
char. force
relative disp.
active moment
\(~\mu_a~~=~\dfrac{\rho\,df_o}{B/L^2}\)
\(~\mu~~~~=~\dfrac{Kd^2}{B/L^2}\)
\(~\alpha~~~~=~~~\pi_o\tau_o\)
\(~f^*~~\,=~~~f_o/f_c\)
\(~\zeta~~~\;\,=~~~d/v_o\tau_o\)
dimensional
attachment rate
System I/O
motor
asymm.
\(f(\alpha)\)
active moment
\(\mu_a\)
sperm number
\(\text{Sp}\)
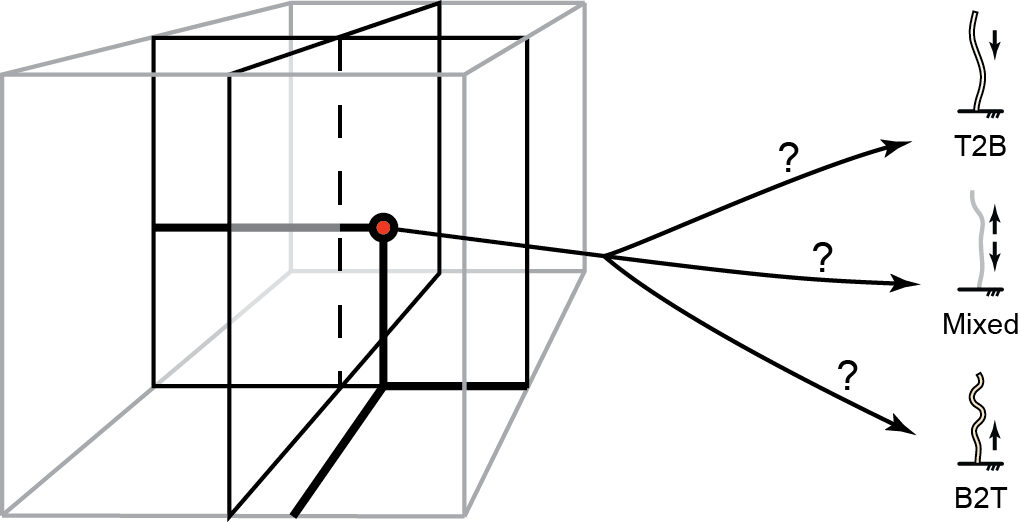
Ramping up the Motor Activity
fixing all parameters except \(\text{Sp}\) and dimensionless activity \(\mu_a\), we see that sliding control give rise to
- a Hopf bifurcation where instability induces sustained oscillations
- larger activity give rise to a 2nd transition from T2B to B2T waves
- the transition zone can show mixed wave states, especially under added thermal noise*
sperm number
active moment
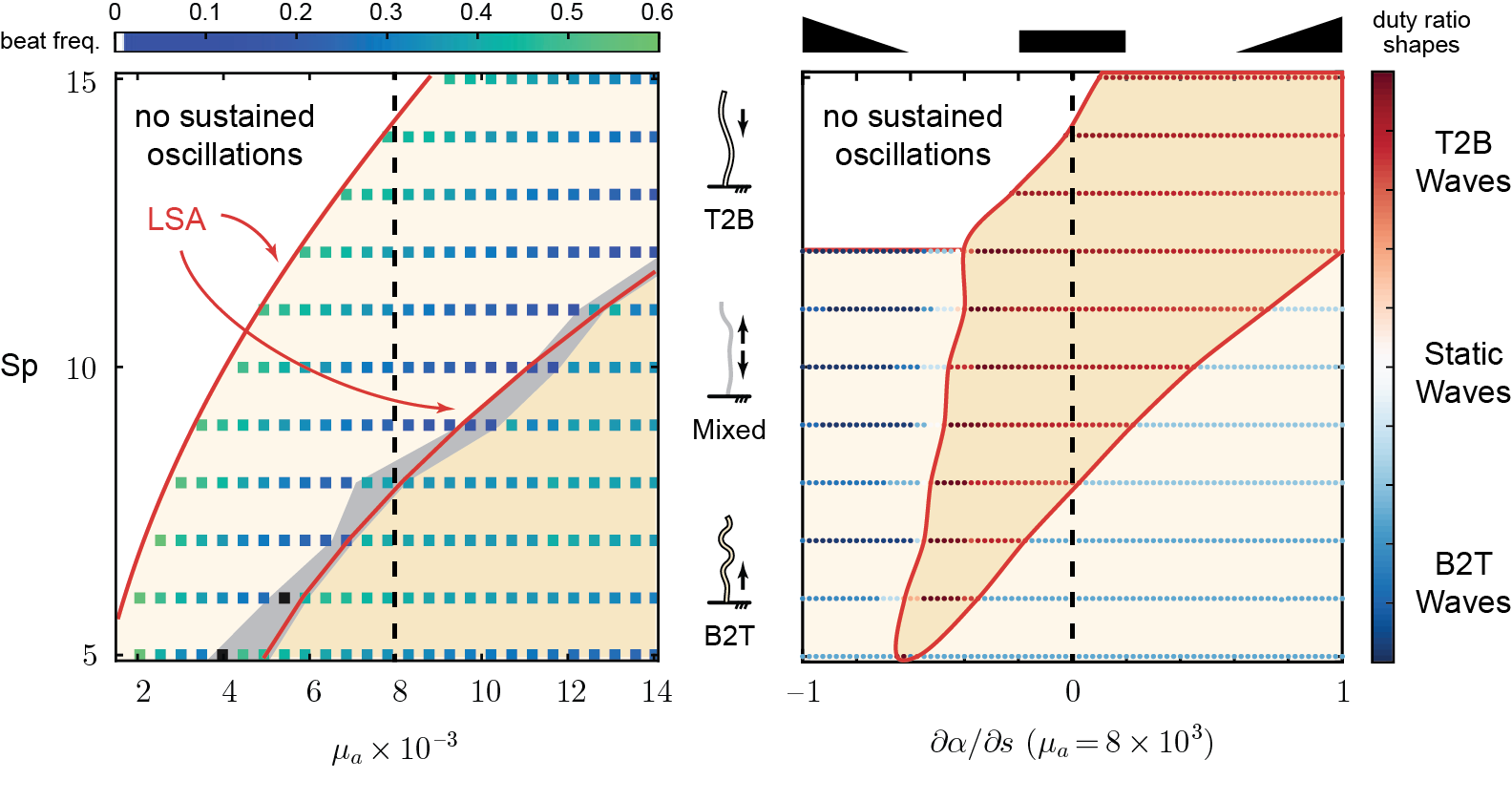
Biasing the Attachment Rate
If we fix \(\mu_a\) but vary the attachment duty ratio \(\alpha\) linearly as a function of arclength \(s\)
- more activity near the base, or [\(\partial\alpha/\partial s>0\)], leads to base-to-tip B2T waves
- more activity near the tip, or [\(\partial\alpha/\partial s<0\)], leads to tip-to-base T2B waves
\(\text{Sp}=10\)
\(\text{Sp}=10\)
\(\text{Sp}=10\)
sperm number
motor asymm.
\(n_+\)
\(n_-\)
\(n_+\)
\(n_-\)
\(n_+\)
\(n_-\)




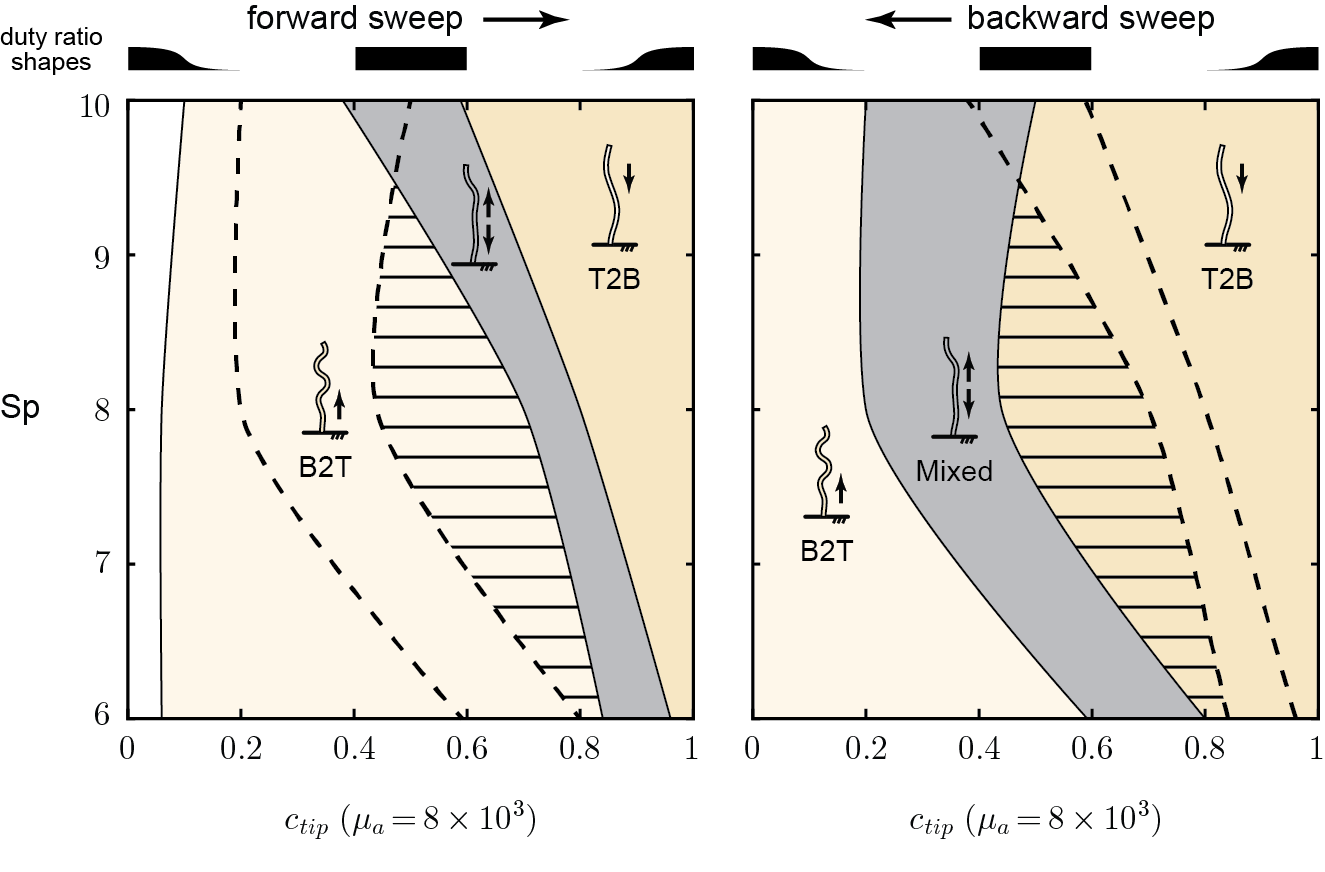
Controlling Wave Reversals
-
previous results suggests that bi-stability zones could exist
-
if we gradually vary from a base-heavy activity profile (\(\alpha_{prox}(s)\)) to a tip-heavy profile (\(\alpha_{dist}(s)\)) and back, we should observe
-
B2T waves \(\rightarrow\) mixed waves \(\rightarrow\) T2B waves \(\rightarrow\) mixed waves \(\rightarrow\) B2T waves
-
proximal dynein / distal dynein
Edwards et al., PNAS (2018)
\(s\)
\(\alpha(s) = (1-c_{tip})\cdot\alpha_{prox}(s)\)
\(+\;c_{tip}\cdot\alpha_{dist}(s)\)
\(\alpha\)
\(s\)
- Trypanosome flagellum contains two distinct families of dynein motors, each built from two ends and meet in the middle.
- Inspired by this, we tested two different way of changing motor activity along the arclength \(s\)

proximal dynein / distal dynein
Edwards et al., PNAS (2018)
Two ways to switch
translating bump
switch between two groups
\(\alpha\)
\(s\)
\(s\)
\(s\)
Controlling Wave Reversals
B2T waves are possible even when activity concentrates near the tip! And the opposite is also true!
\(\text{Sp}=8\)
\(\mu_a=8\times 10^3\)
\(n_+\)
\(n_-\)
\(\text{Sp}=8\)
\(\mu_a=8\times 10^3\)
\(\mathbf{f}_h\cdot \mathbf{n}\)
\(\mathbf{f}_h\cdot\mathbf{n}\)
\(n_+\)
\(n_-\)
Bistable Zones
motor activity distributed in the shaded region can support both B2T and T2B waves!
sperm number
motor asymm.
-
increase in total activity magnitude introduces a T2B to B2T transition under sliding control*
-
biasing activity at either end leads to wave initiations near that end in general, e.g., base heavy activity \(\rightarrow\) B2T waves
-
there exists a bi-stable region where same activity pattern can produce different wave propagation directions
How activity affect wave directions
-
comparable to real data, but
-
difficult to estimate accurate activity parameters and characteristic scales in geometric feedback
-
-
other chemical details† and 3D geometrical effects could further complicate this story
Some Concluding Remarks
-
results discussed utilize only sliding control
-
combination of different feedback mechanism might better explain diverse behaviors
-
-
effects on propulsive efficiency*
-
LSA about traveling wave states
Experimental observations
-
B2T waves can be triggered by either a lack of tip motors or more Ca\(^{2+}\)
-
T2B waves at higher frequency => faster straight swimming
-
(asymmetric) B2T waves are at larger amplitude but much slower frequency => helical slow swimming
-
Geometric clutch theories are popular but there are separate evidences on how curvature/sliding control fits wave shapes better
Curvature Control
-
Wave direction change is impossible without changing direction of motor detachment
-
frequency (slowly) increases with increased activity
-
do not produce (very) large amplitude waveforms
Sliding control
-
Base-to-tip wave can be triggered by either a lack of tip activity or an increase in "activity"
-
Tip-to-base wave produces smaller net forces (slower swimming)
-
frequency decreases with "activity increase"
Comparing with Experiments
-
Show/prove why direction cannot change under curvature control?
-
Construct a threshold-based sliding control analytical model assume
-
\[\theta(s,t) = T(s) \sin(ks-\omega t)\]
-
\[m_a(s,t) = M(s) \sin(ks-\omega t)\]
-
\[n_+(s,t) = N(s) \sin(ks-\omega t)\]
-
\[n_-(s,t) = N(s) \cos(ks-\omega t)\]
-
-
2 DiffEQs coupling T,M w/ BCs (linearized elastic filament eqn)
-
1 Eqn coupling M and N and T (expression of active torque)
-
1 Eqn coupling N and T (dynamics on motor)
Analytical model for intuitive explanations?
Tanhks 4 Yo Attention
Funding Sources:


