Surface Growth and Patterns

\(\frac{\partial}{\partial s}q_1 + k_2 q_3 - k_3 q_2 = \lambda \omega_2\),
\(\frac{\partial}{\partial s}q_2 + k_3 q_1 - k_1 q_3 = -\lambda \omega_1\),
\(\frac{\partial}{\partial s}q_3 + k_1 q_2 - k_2 q_1 = -\frac{\partial}{\partial t} \lambda\),
\(\frac{\partial}{\partial t} k_1-\frac{\partial}{\partial s}\omega_1=k_2\omega_3-k_3\omega_2\),
\(\frac{\partial}{\partial t} k_2-\frac{\partial}{\partial s}\omega_2=k_3\omega_1-k_2\omega_3\),
\(\frac{\partial}{\partial t} k_3-\frac{\partial}{\partial s}\omega_3=k_1\omega_2-k_2\omega_1\)
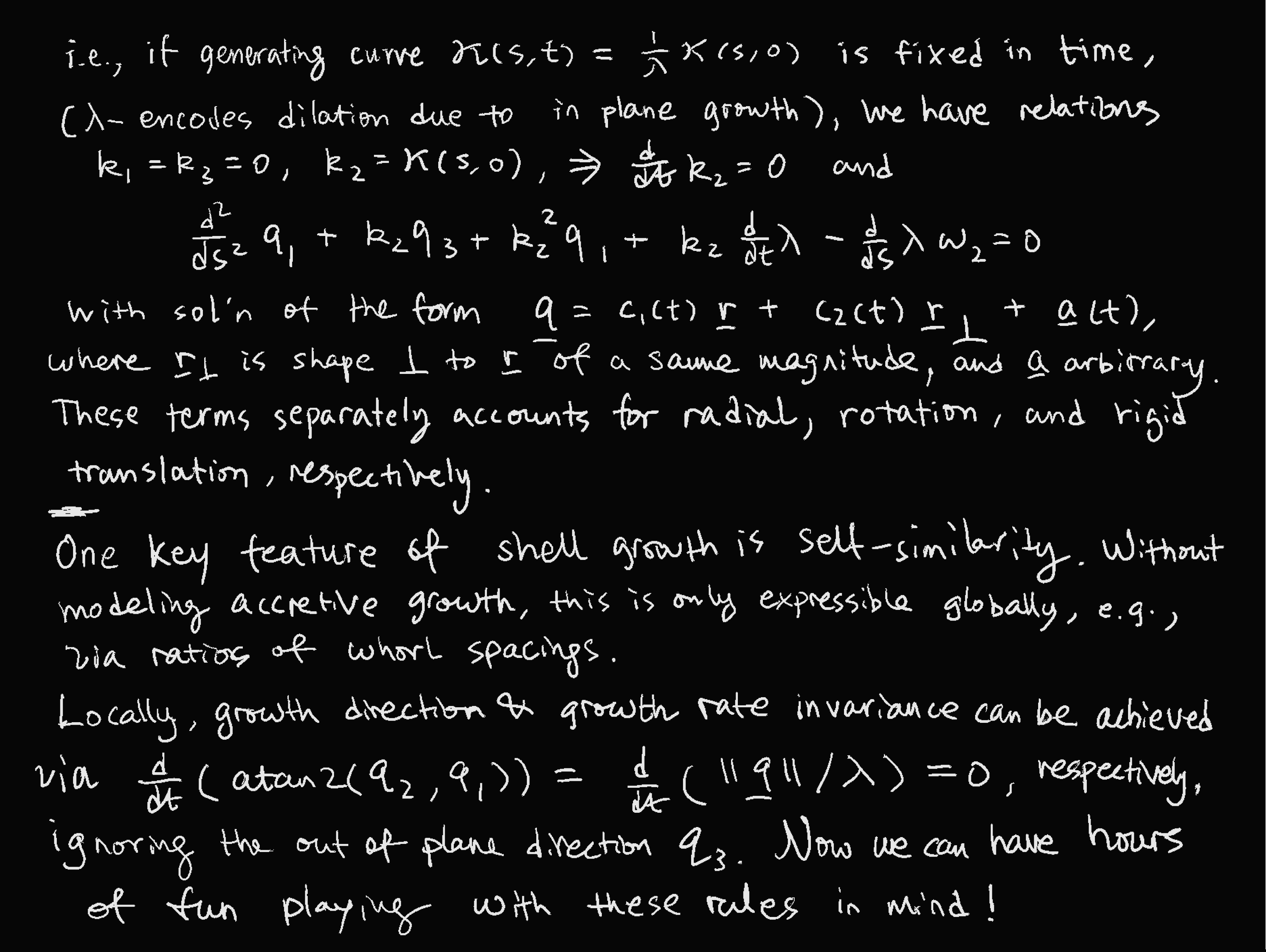
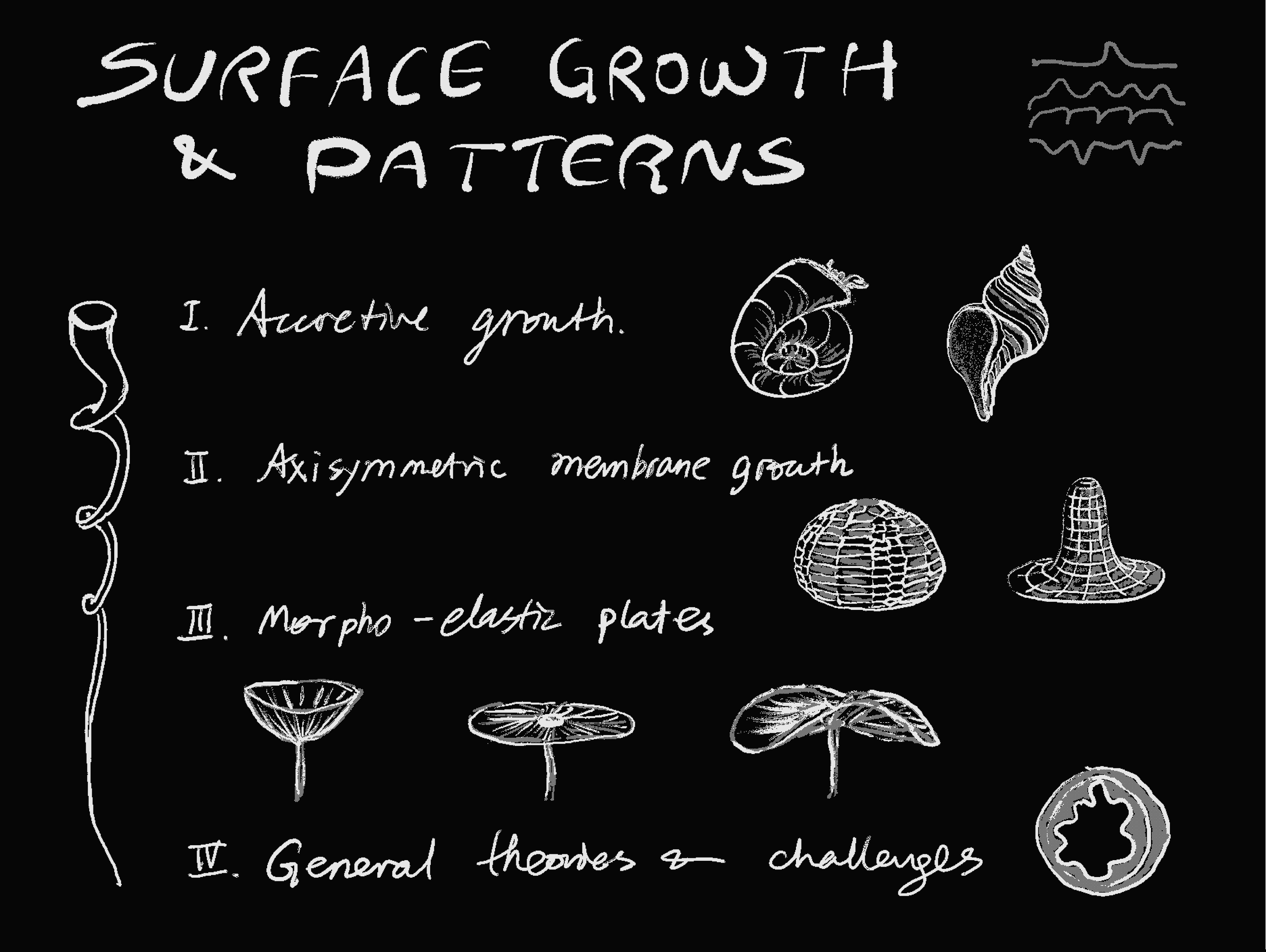
%% Kinematics of Surface Accretive Growth
clear; figure(1); % close all;
mycross = @(a,b) [a(:,2).*b(:,3)-a(:,3).*b(:,2), ...
                  a(:,3).*b(:,1)-a(:,1).*b(:,3), ...
                  a(:,1).*b(:,2)-a(:,2).*b(:,1)];
% vectnormalize = @(v) v./sqrt(sum(v.^2,2));
rad2deg = 180/pi;
explicit = true;
% explicit = false;
%% shape parameters
Nt = 1e3;
dt = 1e-3;
rgap = 10; % need to divide 360
isHalf = false;
s = linspace(0,359,360)'; % angles in one revolution
r0 = [cosd(s),sind(s),zeros(size(s))]/10; % generating shape (circle)

% Cylinder
q1 = @(t) 0;
q2 = @(t) 1;
q3 = @(t) 0;

% Twisted Cone
% q1 = @(t) -.5;
% q2 = @(t) 1;
% q3 = @(t) .5;

% Logarithmic Coil
% dt = 1e-2;
% q1 = @(t) -.1;
% q2 = @(t) (pi+1*cosd(s));
% q3 = @(t) 0;

% Turitella 1
% dt = 1e-2;
% rgap = 2;
% R = .1 + 0.0002*cosd(20*s);
% r0 = R.*[cosd(s), sind(s), zeros(size(s))];
% q1 = @(t) -.1*exp(-.1*t^2);
% q2 = @(t) 1+1*cosd(s);
% q3 = @(t) .5;

% Turitella 2
% dt = 1e-2;
% rgap = 10;
% r0 = [cosd(s),sind(s),zeros(size(s))]/10;
% q1 = @(t) -.1*exp(-.1*t^2);
% q2 = @(t) 1+1*cosd(s-1.5*t*rad2deg);
% q3 = @(t) 0;

% Horn
% Nt = 5e2;
% dt = 5e-3;
% k = @(t) 0.25+0.02*t;
% r0 = [cosd(s),sind(s),zeros(size(s))]/10;
% rgap = 90;
% q1 = @(t) 0.04 - k(t)*sind(s);
% q2 = @(t) 0.75 + 0.2*cosd(s);
% q3 = @(t) k(t)*cosd(s);

% Conch
% Nt = 5e2;
% dt = 1e-2;
% rgap = 2;
% isHalf = true;
% R = 1 + 0.01*cosd(20*s);
% r0 = R.*[2*cosd(s), sind(s), zeros(size(s))];
% q1 = @(t) -abs(R.*cosd(2*s));
% q2 = @(t) 0.1+8*R.*sind(s);
% q3 = @(t) R.*sind(s);

% Bivalve
% dt = 1e-2;
% rgap = 2;
% isHalf = true;
% R = 1 + 0.05*cosd(16*s);
% r0 = R.*[cosd(s), sind(s), zeros(size(s))];
% q1 = @(t) -3;
% q2 = @(t) .1 + 5*(1-.1*t)*R.*sind(s);
% q3 = @(t) 0;

% Ammonite
% dt = 1e-3;
% isHalf = false;
% Nt = 2.8e3;
% rgap = 10;
% r0 = [cosd(s),sind(s),zeros(size(s))]/10;
% kg = @(t) 1+4*cos(150*t); % should be k_g of eqn (7.66)-(7.67)
% q1 = @(t) -.13*(1-1*exp(-10*t)).*kg(t);
% q2 = @(t) (pi+(1.05+2*exp(-t))*cosd(s));
% q3 = @(t) -.05*exp(-.1*t^2);
%% explicit planar shape invariant stepping
if explicit
r = r0;
track1 = zeros(Nt,3);
track2 = zeros(Nt,3);
track1(1,:) = r(1,:);
track2(1,:) = r(181,:);
lambda = 1;
if isHalf
  Nr = 180;
  shell.v = r((0:rgap:Nr)+1,:);
  f_1layer = [1:Nr/rgap; 2:Nr/rgap+1];
else
  Nr = 360;
  shell.v = r((0:rgap:Nr-1)+1,:);
  f_1layer = [1:Nr/rgap; 2:Nr/rgap 1];
end
shell.f = [];
shell.t = zeros(Nr/rgap+isHalf*1,1);

% figure('position',[0 0 1e3 1e3]);
clf; set(gcf,'position',[0 0 1e3 1e3]);
hold all; axis tight; axis equal; axis off; view(3); camlight; material dull
light('Position',[-1 0 0],'Style','local')
light('Position',[270 -10 -1],'Style','local')
ph = patch('faces',shell.f,'vertices',shell.v,'facevertexCData',shell.t,...
  'facecolor','interp','edgecolor','none','FaceLighting','gouraud');
if ~isHalf
t1h = plot3(track1(:,1),track1(:,2),track1(:,3),'k','linewidth',2);
t2h = plot3(track2(:,1),track2(:,2),track2(:,3),'r','linewidth',2);
end

for i = 1:Nt
% for i = 1
  lambda_old = lambda;
  medial_old = mean(r,1);
%   basis_old = basis;
  
  t = (i-1)*dt;
  [T,N,B] = FrenetSerret(r,s,false); % not assuming planar director frames yet
  dr = q1(t).*N + q2(t).*B + q3(t).*T;
  rnew = r + dr*dt; % naive stepping (very unstable)
  
  % recalculate assuming planarity and shape invariance
  medial = mean(rnew,1); % new medial position
  lambda = norm(diff(rnew([0 180]+1,:),1))/2; % naive dilation factor
  lnodilate = r + (q2(t).*B + q3(t).*T)*dt; % growth without dilation
  lnodilate = norm(diff(lnodilate([0 180]+1,:),1))/2; % size error from finite time stepping
  lambda = lambda/lnodilate*lambda_old; % corrected dilation
  basis = vectnormalize(rnew([0 90]+1,:) - medial); % new planar basis
  r = lambda*(basis(1,:).*r0(:,1) + basis(2,:).*r0(:,2)) + medial;
  
  track1(i,:) = r(1,:);
  track2(i,:) = r(181,:);
  if isHalf
    shell.v = [shell.v; r((0:rgap:Nr)+1,:)];
  else
    shell.v = [shell.v; r((0:rgap:Nr-1)+1,:)];
  end
  shell.f = [shell.f; [f_1layer; flipud(f_1layer)+Nr/rgap]'+Nr*(i-1)/rgap];
  shell.t = [shell.t; ones(Nr/rgap+isHalf*1,1)*t];
  if ~mod(i,1e2) || i==1
    if ~isHalf
    set(t1h,'xdata',track1(:,1),'ydata',track1(:,2),'zdata',track1(:,3));
    set(t2h,'xdata',track2(:,1),'ydata',track2(:,2),'zdata',track2(:,3));
    end
    set(ph,'faces',shell.f,'vertices',shell.v,'facevertexCData',shell.t);
    drawnow;
  end
end
else
%% direct numerical integration (can be unstable)
[tt,rsol] = ode45(@(t,y) growth(t,y,s,q1,q2,q3),linspace(0,Nt*dt,Nt),reshape(r0,[],1));
% [tt,rsol] = ode15s(@(t,y) growth(t,y,s,q1,q2,q3),linspace(0,Nt*dt,Nt),reshape(r0,[],1));

r = reshape(rsol(1,:),[],3);
track1 = zeros(Nt,3);
track2 = zeros(Nt,3);
track1(1,:) = r(1,:);
track2(1,:) = r(181,:);
lambda = 1;
if isHalf
  Nr = 180;
  shell.v = r((0:rgap:Nr)+1,:);
  f_1layer = [1:Nr/rgap; 2:Nr/rgap+1];
else
  Nr = 360;
  shell.v = r((0:rgap:Nr-1)+1,:);
  f_1layer = [1:Nr/rgap; 2:Nr/rgap 1];
end
shell.f = [];
shell.t = zeros(Nr/rgap+isHalf*1,1);

% figure('position',[0 0 1e3 1e3]);
clf; set(gcf,'position',[0 0 1e3 1e3]);
hold all; axis tight; axis equal; axis off; view(3); camlight; material dull
light('Position',[-1 0 0],'Style','local')
ph = patch('faces',shell.f,'vertices',shell.v,'facevertexCData',shell.t,...
  'facecolor','interp','edgecolor','none','FaceLighting','gouraud');
t1h = plot3(track1(:,1),track1(:,2),track1(:,3),'k','linewidth',2);
t2h = plot3(track2(:,1),track2(:,2),track2(:,3),'r','linewidth',2);

for i = 1:Nt
  t = tt(i);
  r = reshape(rsol(i,:),[],3);
  track1(i,:) = r(1,:);
  track2(i,:) = r(181,:);
  if isHalf
    shell.v = [shell.v; r((0:rgap:Nr)+1,:)];
  else
    shell.v = [shell.v; r((0:rgap:Nr-1)+1,:)];
  end
  shell.f = [shell.f; [f_1layer; flipud(f_1layer)+Nr/rgap]'+Nr*(i-1)/rgap];
  shell.t = [shell.t; ones(Nr/rgap+isHalf*1,1)*t];
  if ~mod(i,1e2) || i==1
    if ~isHalf
    set(t1h,'xdata',track1(:,1),'ydata',track1(:,2),'zdata',track1(:,3));
    set(t2h,'xdata',track2(:,1),'ydata',track2(:,2),'zdata',track2(:,3));
    end
    set(ph,'faces',shell.f,'vertices',shell.v,'facevertexCData',shell.t);
    drawnow;
  end
end
end

function [drr] = growth(t,rr,s,q1,q2,q3)
  r = reshape(rr,[],3);
  [T,N,B] = FrenetSerret(r,s,true);
  dr = q1(t).*N + q2(t).*B + q3(t).*T;
  drr = reshape(dr,[],1);
end
%% utility functions
function [T,N,B] = FrenetSerret(r,s,planar)
mycross = @(a,b) [a(:,2).*b(:,3)-a(:,3).*b(:,2), ...
                  a(:,3).*b(:,1)-a(:,1).*b(:,3), ...
                  a(:,1).*b(:,2)-a(:,2).*b(:,1)];
% vectnormalize = @(v) v./sqrt(sum(v.^2,2));
% mygrad = @(v,s) (circshift(v,-2)-v)./mod((circshift(s,-2)-s),360);
mygrad = @(v,s) (circshift(v,-1)-circshift(v,1))./mod((circshift(s,-1)-circshift(s,1)),360);

T = zeros(size(r)); N = zeros(size(r));
for i = 1:3
  T(:,i) = mygrad(r(:,i),s);
end
T = vectnormalize(T);

if planar % assumes planarity
  medial = mean(r,1);
  b = mean(vectnormalize(mycross(r(91,:)-medial,r(1,:)-medial)),1); % assume planarity
  N = vectnormalize(mycross(T,b));
  B = repmat(b,numel(s),1);
else
  for i = 1:3
    N(:,i) = mygrad(T(:,i),s);
  end
  N = vectnormalize(N);
  B = mycross(T,N);
end

end

function vhat = vectnormalize(v)
  vnorm = sqrt(sum(v.^2,2));
  vhat = v./vnorm;
  vhat(vnorm==0,:) = 0;
end
Have fun playing with this code!