Multiscale modeling of Cilia Coordination
Feng Ling
Kanso Bio-inspired Motion Lab, USC
April 23, 2022
SoCal Fluids
Why cilia?
Motile cilia are microscopic hair-like protrusions that direct fluid flow for many Eukaryotic life.

5μm
Daghlian (2006)

K.Y. Wan (2018)
10μm
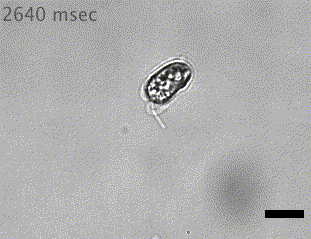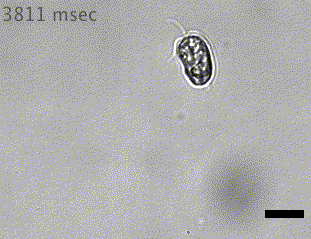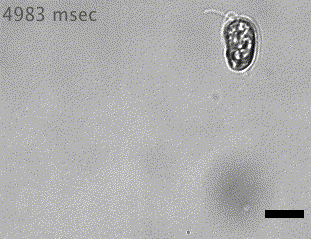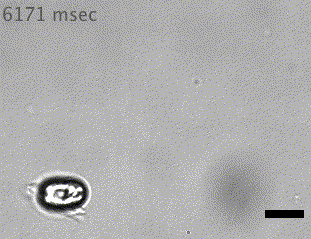
Quadflagellate
Wan (2019)
30μm
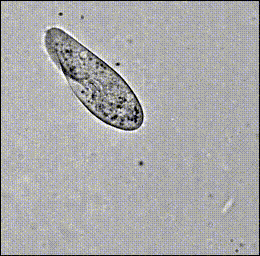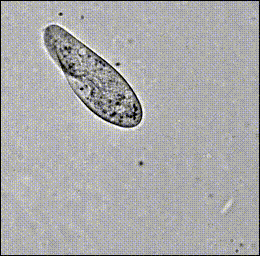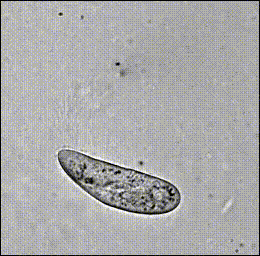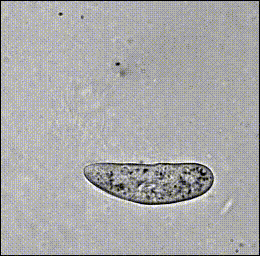
Hamel, et al. (2010)
Paramecium
Coordination for diverse functions
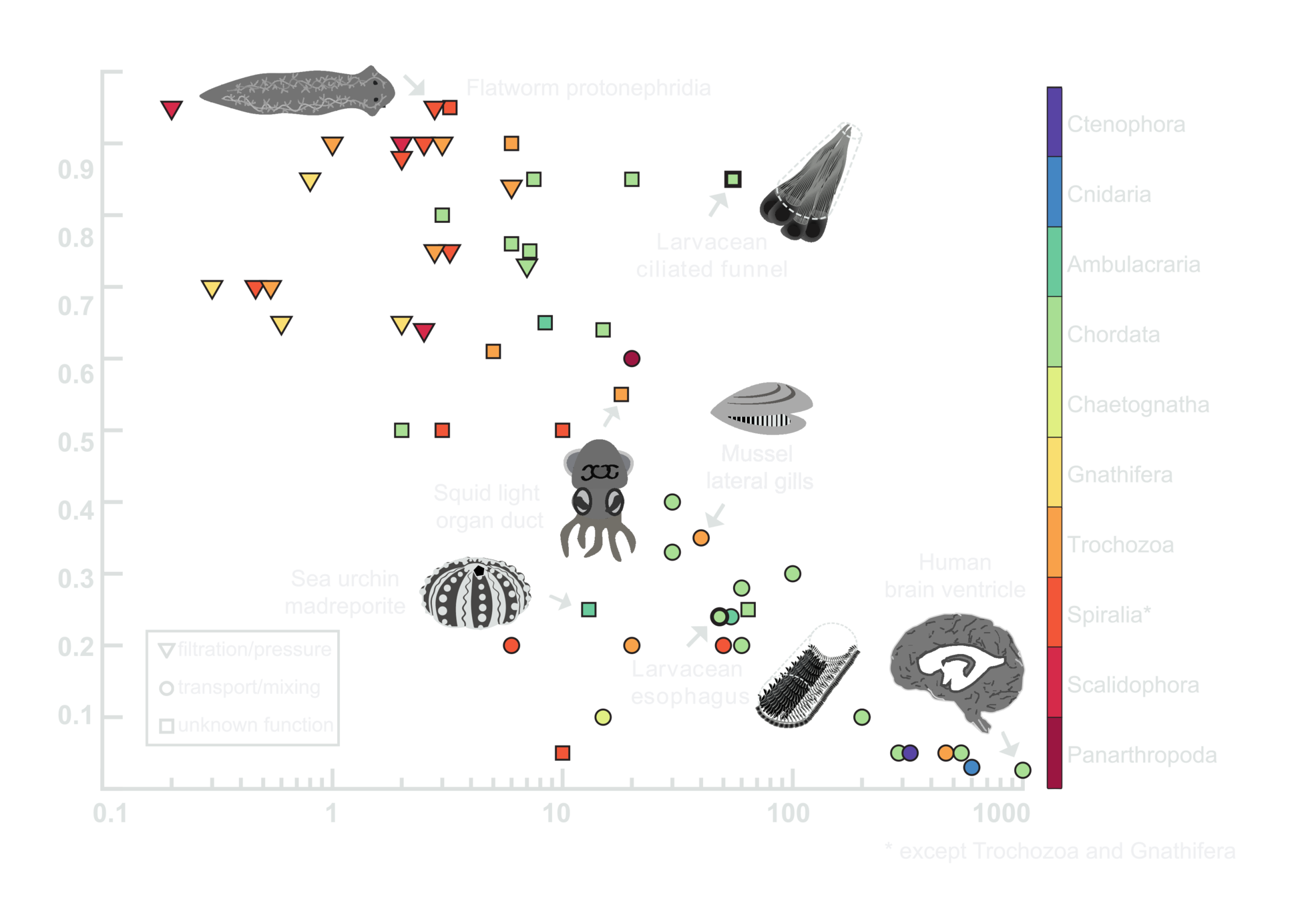
30μm
Squid Light Organ
Nawroth, Guo, et al. (2017)
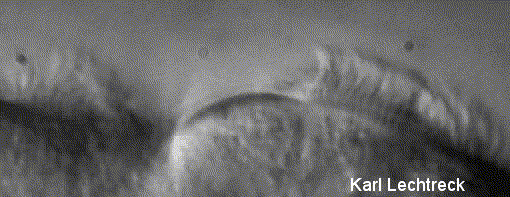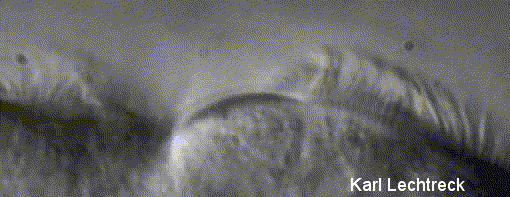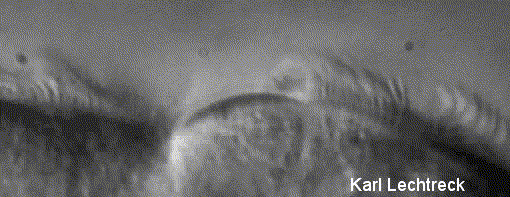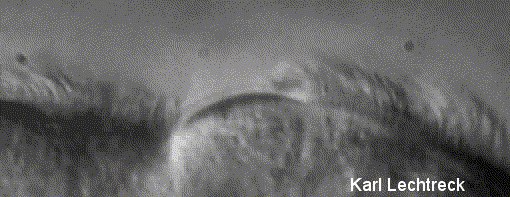
Lechtreck (2000)
Mouse Airway
10μm

Multi-synchrony for distinct swimming gaits
Coherent coordination for specialized functions
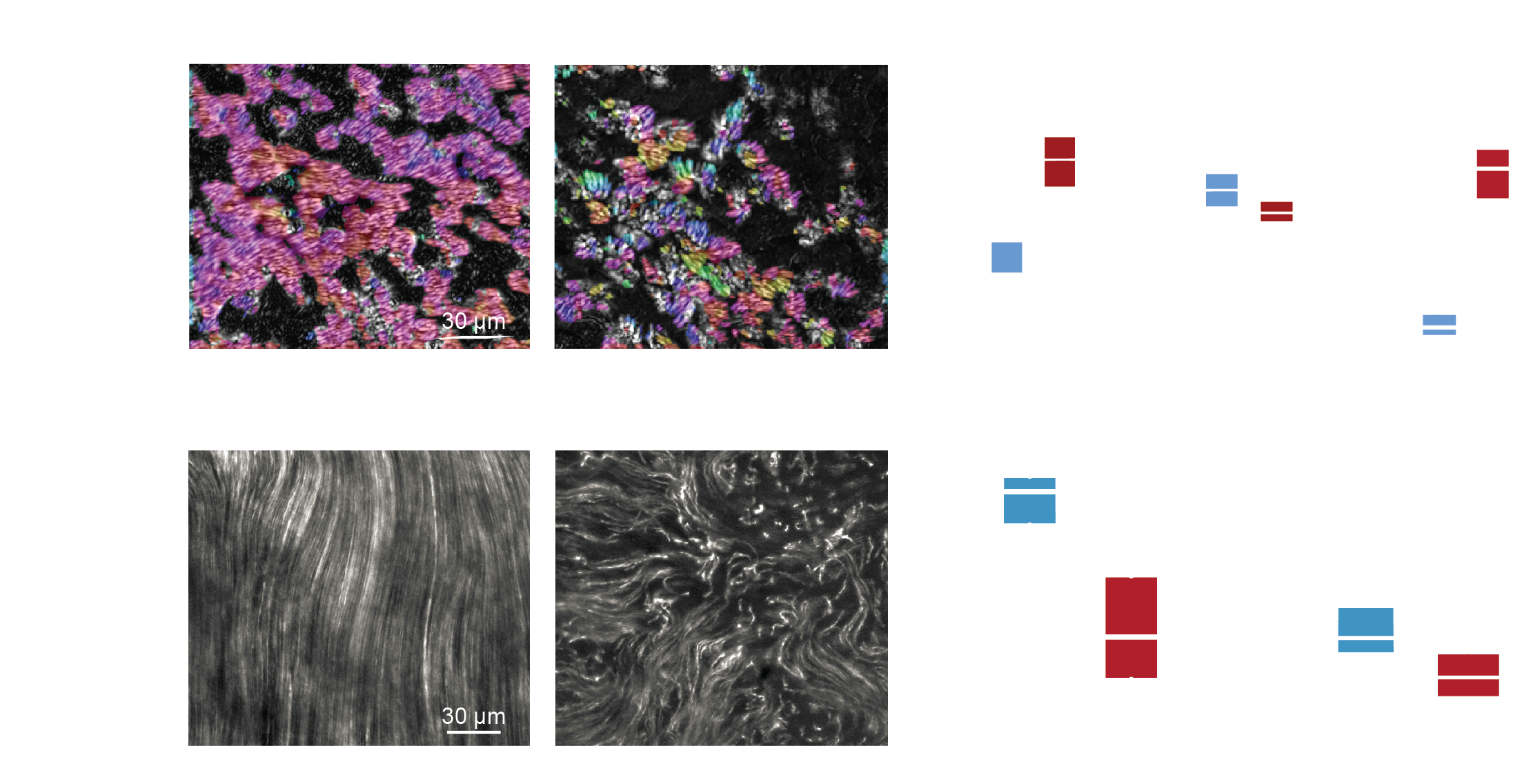
Nawroth, et al. (unpublished)
healthy
inflamed (IL13)
structure
function

less cilia
less coherent beat pattern
more eddies
slower flow
in-vitro human airway tissue
More than scientific curiosities
Understanding tissue- and organ-level functions of cilia have direct consequences on human health and disease!
The key is to enable functional prediction from structural observations!

Multiscale models for multiscale physics

To obtain principled understanding of cilia requires studying them across many length scales
Multiscale models for multiscale physics

-
1 mm\(^2\) of tissue can have a million cilia, and each driven by thousands of motor protein complexes!
-
Different abstraction levels are both necessary and desirable to truly understand cilia
Cilia Coordination
Guo, Man, et al., R. S. Interface (2020)
Man, Kanso, PRL (2020)
Kanale, Ling, et al., In preparation (2022)
Cilia Oscillation
Ling, Guo, Kanso, R. S. Interface (2018)
Man, Ling, Kanso, Phil. Trans. B (2020)
Ling, Kanso, In preparation (2022)
Ciliary Function
Guo, Ding, et al., JFM,PRE… (2014-2017)
Nawroth, Guo et al., PNAS (2017)
Nawroth, et al., Phil. Trans. B (2020)
Nawroth, Ling, et al., Submitted (2022)


Multiscale models for multiscale physics

-
1 mm\(^2\) of tissue can have a million cilia, and each driven by thousands of motor protein complexes!
-
Different abstraction levels are both necessary and desirable to truly understand cilia
Cilia Coordination
Guo, Man, et al., R. S. Interface (2020)
Man, Kanso, PRL (2020)
Kanale, Ling, et al., In preparation (2022)
Cilia Oscillation
Ling, Guo, Kanso, R. S. Interface (2018)
Man, Ling, Kanso, Phil. Trans. B (2020)
Ling, Kanso, In preparation (2022)
Ciliary Function
Guo, Ding, et al., JFM,PRE… (2014-2017)
Nawroth, Guo et al., PNAS (2017)
Nawroth, et al., Phil. Trans. B (2020)
Nawroth, Ling, et al., Submitted (2022)


Phenomenological model of cilia oscillation
-
Postulate: exact driving mechanism of cilia matter little when studying cilia coordination
-
e.g., symmetric cilia beats reproduced by follower force driven filament (Man 2020)
-
Condense to two non-dimensional ratios:
\(F=\|\bm{f}\|/(B/L^3)\) \(\rightarrow\) activity level
\(\gamma=\ln(L/h)/\ln(L/a)\) \(\rightarrow\) coupling strength
with an emergent time scale \(t_o=\zeta L^4/B\)
-
Man, Kanso, PRL (2020)
\(a\)

\(h\)
\(L\)
\(\bm{f}\)
Phenomenological model of cilia oscillation
-
Postulate: exact driving mechanism of cilia matter little when studying cilia coordination
-
e.g., symmetric cilia beats reproduced by follower force driven filament (Man 2020)
-
Condense to two non-dimensional ratios:
\(F=\|\bm{f}\|/(B/L^3)\) \(\rightarrow\) activity level
\(\gamma=\ln(L/h)/\ln(L/a)\) \(\rightarrow\) coupling strength
with an emergent time scale \(t_o=\zeta L^4/B\)
-
-
reveals multi-synchrony and bistability for a pair of hydrodynamically coupled cilia

initially in-phase
initially anti-phase
Man, Kanso, PRL (2020)

in-phase
anti-phase
Phenomenological model of cilia oscillation
-
Postulate: exact driving mechanism of cilia matter little when studying cilia coordination
-
e.g., symmetric cilia beats reproduced by follower force driven filament (Man 2020)
-
Condense to two non-dimensional ratios:
\(F=\|\bm{f}\|/(B/L^3)\) \(\rightarrow\) activity level
\(\gamma=\ln(L/h)/\ln(L/a)\) \(\rightarrow\) coupling strength
with an emergent time scale \(t_o=\zeta L^4/B\)
-
-
reveals multi-synchrony and bistability for a pair of hydrodynamically coupled cilia
initially in-phase
initially anti-phase
Man, Kanso, PRL (2020)

in-phase
anti-phase

Stability analysis as phased oscillators
- Assuming coupled filaments always follow the same trajectory but at a different phase (Kuramoto reduction*), we can write an evolution equation of the phase difference \(\Delta\theta\):\[\partial_t(\Delta\theta) = \gamma\omega\Psi(\Delta\theta)\]
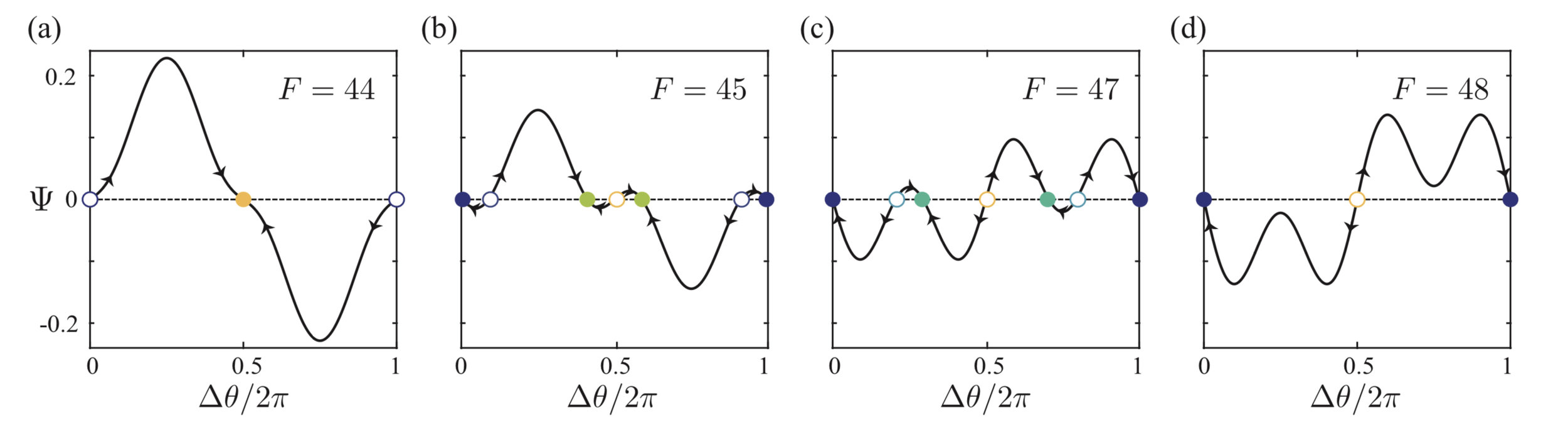
Man, Kanso, PRL (2020)
Kawamura, Tsubaki, PRE (2018)
in-phase
anti-phase
non-trivial
pitchfork bifurcations
saddle-node bifurcations
(weak hydrodynamic coupling)
Stability analysis as phased oscillators
- Assuming coupled filaments always follow the same trajectory but at a different phase (Kuramoto reduction*), we can write an evolution equation of the phase difference \(\Delta\theta\):\[\partial_t(\Delta\theta) = \gamma\omega\Psi(\Delta\theta)\]

Man, Kanso, PRL (2020)
Kawamura, Tsubaki, PRE (2018)
in-phase
anti-phase
non-trivial
pitchfork bifurcations \(\rightarrow\)
saddle-node bifurcations \(\rightarrow\)
weak hydrodynamic coupling
How much can phased oscillator theory help us in understanding synchronization of many, many cilia?
\(\theta_i\)
⤸

-
Effective strokes / rotor tilt
\(\rightarrow\) first-harmonic forcing -
Planar beats / rotor eccentricity
\(\rightarrow\) second harmonic forcing -
Planar circular rotor with first and second harmonic forcing
-
matches far-field flow
-
do not produce net flow without hydrodynamic interactions
-
Minimalistic description of cilia beat
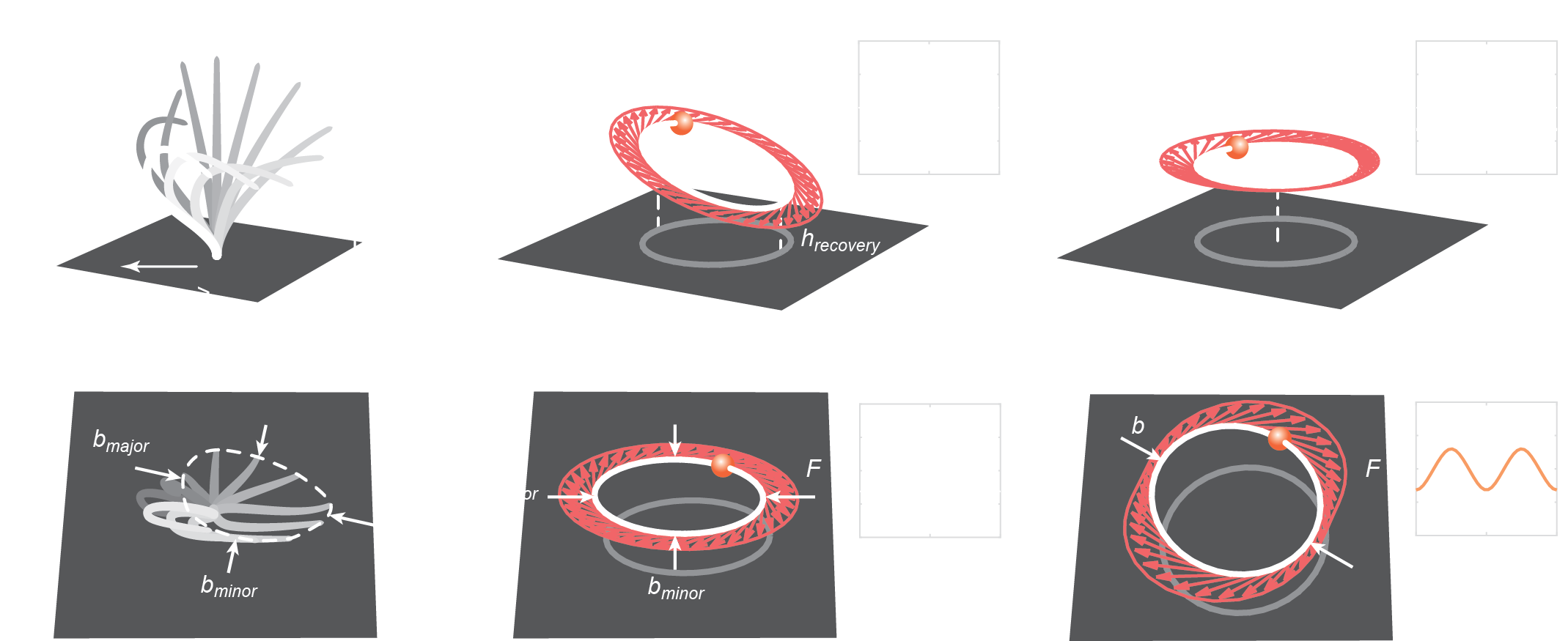


\(\theta_i\)
⤸

Uchida, Golestanian, PRL (2010)
Osterman, Vilfan, PNAS (2011)
Brumley, et al., eLife (2014)
Kanale, Ling, Fuerthauer, et al., (2022)
'cilium-level' activity
-
trajectory geometry
-
forcing coefficient
'tissue-level' organization
-
cilia spacing/density
-
structural order
-
beat coherence
can be solved with Blake tensor, regularized Stokeslet methods, and with a continuum theory!
Periodic boundary
\(\cos(\theta_i)\)
\(-1\) \(1\)
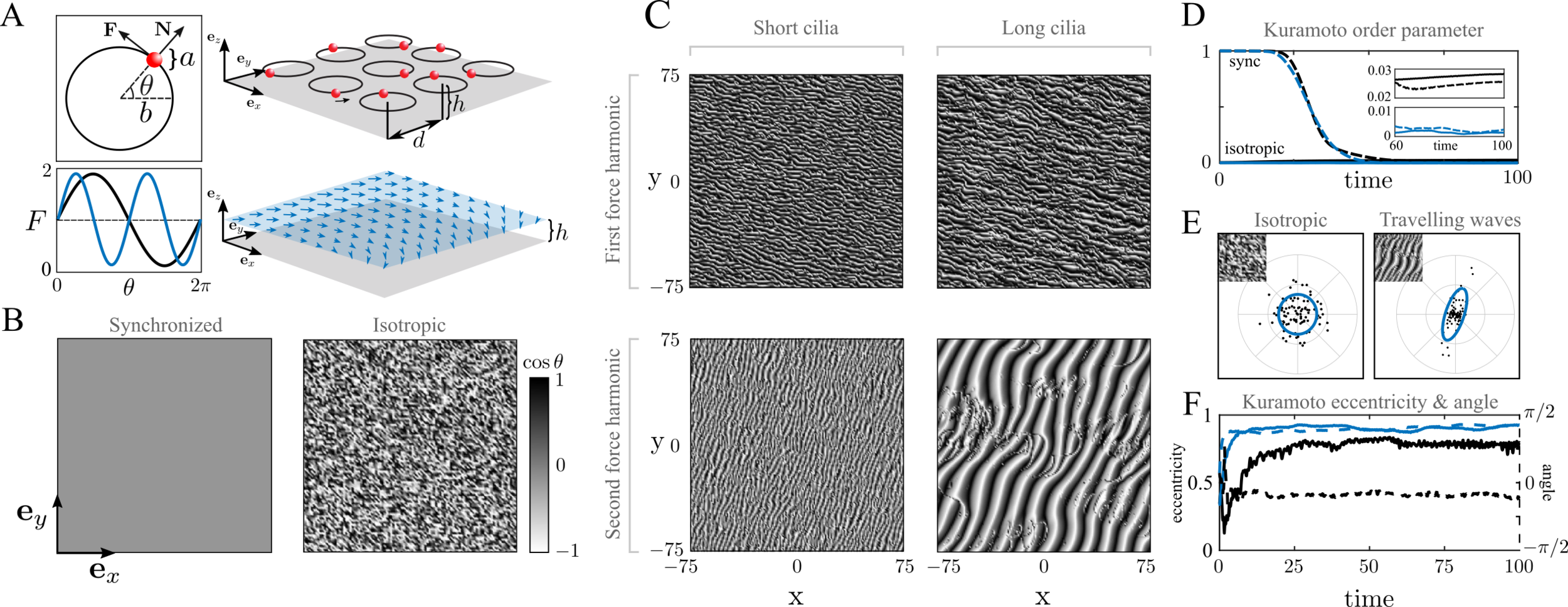


no-slip boundary
\(\theta_i\)
⤸

abstraction
motor activity
Stokes' Flow
Phase oscillator for ciliary carpet
Kanale, Ling, Fuerthauer, Kanso, (2022)
ciliated patches
coverage ratio = 0.5
patch wavenumber = 2
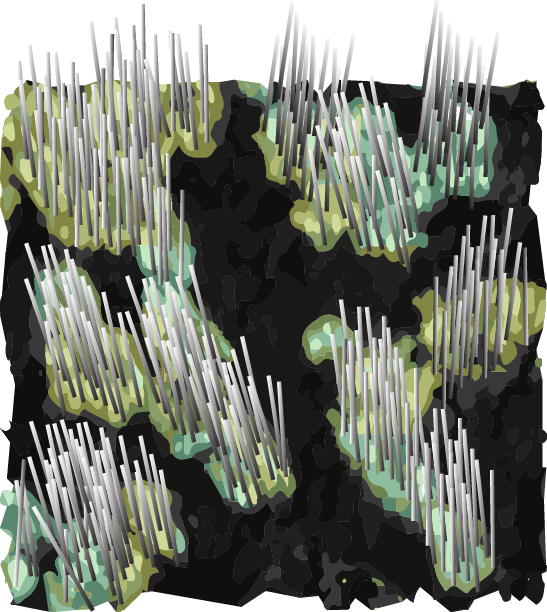
no cilia

no cilia
Heterogeneity for metachronal order
Spherical cow of patches:
- coverage ratio: \(\dfrac{A_{ciliated}}{A_{total}}\)
- patch wavenumber: # of patches along one side of periodic box
- patch disorder: standard deviation of Gaussian displacement (0 for now)
Kanale, Ling, Fuerthauer, Kanso, (2022)


coverage \(C=1\)
coverage \(C= 0.5\), patch number \(n= 4\)
coverage \(C= 0.25\), patch number \(n= 4\)
-
When fully covered, defects and grain boundaries form spontaneously
-
Gaps between patches bring intrinsic 'relief' for defects
Heterogeneity for metachronal order
Kanale, Ling, Fuerthauer, Kanso, (2022)
-
Effect is independent of forcing harmonics
-
More pronounced when rotor are spaced closer (stronger interaction)
Heterogeneity for metachronal order
coverage \(C=1\)
coverage \(C= 0.5\), patch number \(n= 4\)
coverage \(C= 0.25\), patch number \(n= 4\)
Kanale, Ling, Fuerthauer, Kanso, (2022)
22,000+ cilia
short cilia
long cilia
short cilia
long cilia
-
Effective/recovery stroke enforces unidirectional waves
-
Eccentric beating plane promotes metachronal order

\(\cos(\theta_i)\)
\(1\)
\(-1\)
2nd harmonic forcing (eccentric beat / ‘nematic')
1st harmonic forcing (effective stroke / ‘polar’)
Spontaneous metachronal order
Kanale, Ling, Fuerthauer, Kanso, (2022)
short cilia
long cilia
short cilia
long cilia

\(\cos(\theta_i)\)
\(1\)
\(-1\)
Combining the 'polar' and 'nematic' forcing term enable both net pumping and long range synchronization of ciliary carpet simultaneously!
Spontaneous metachronal order
-
Effective/recovery stroke enforces unidirectional waves
-
Eccentric beating plane promotes metachronal order
2nd harmonic forcing ('nematic' force)
1st harmonic forcing ('polar' force)
Kanale, Ling, Fuerthauer, Kanso, (2022)
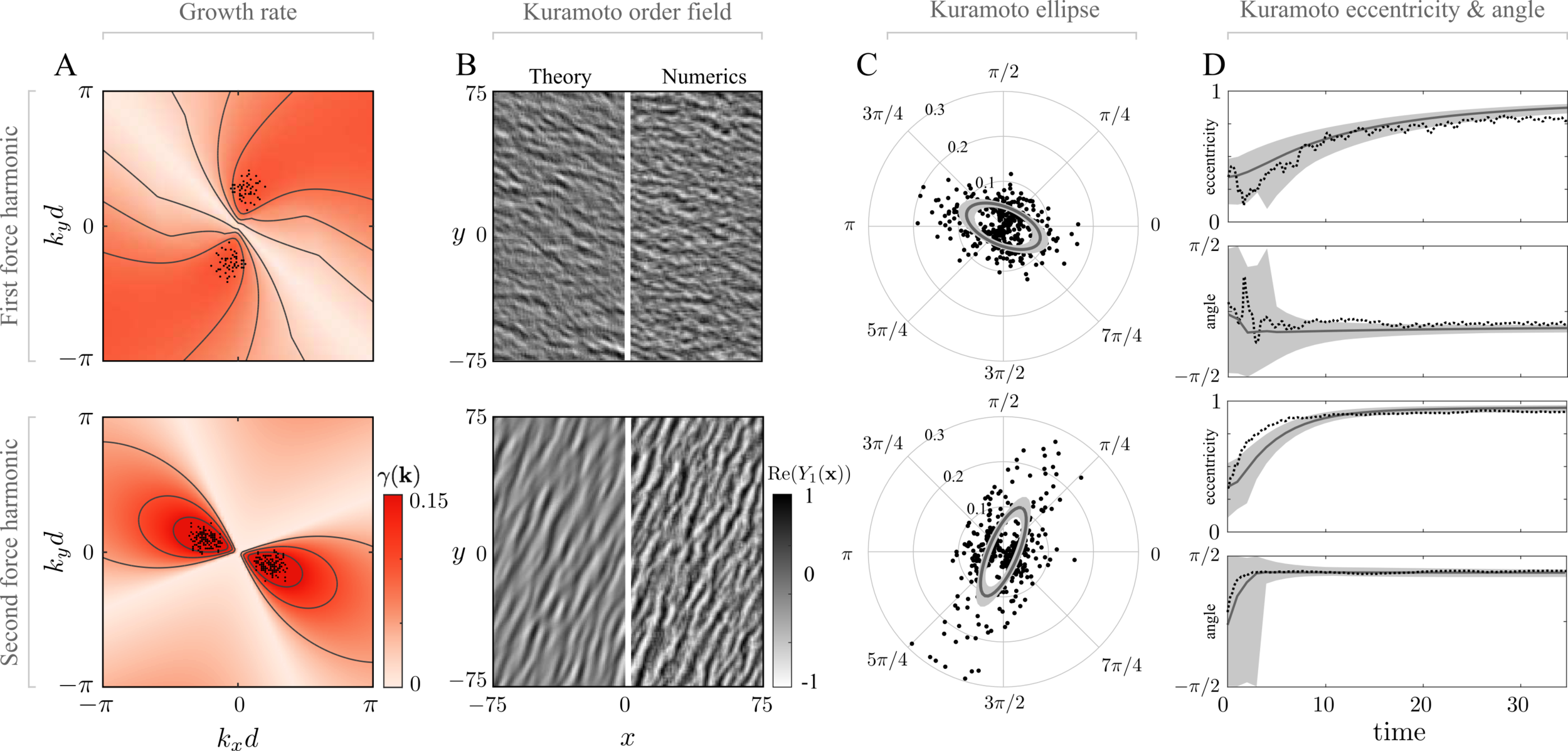

theory / numerics
growth rate
\(k_x\)
\(k_y\)
2nd harmonic forcing


theory / numerics
growth rate
\(k_x\)
\(k_y\)
1st harmonic forcing
Continuum theory for cilia coordination
Linear stability analysis on isotropic initial conditions produces excellent predictions!
Kanale, Ling, Fuerthauer, Kanso, (2022)
Kuramoto order and a continuum theory
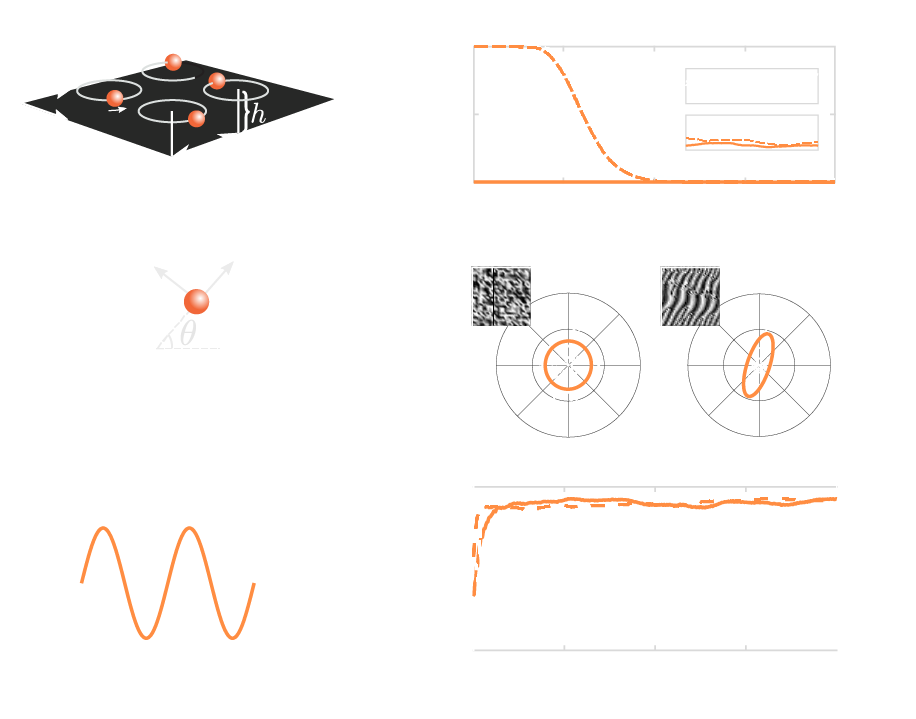
Scalar Kuramoto order parameter cannot distinguish metachronally ordered states:
- coarse-graining local Kuramoto order parameter for a continuum theory
- project into angular variable for wave characteristics (Radon transform)
- eccentricity symbolizes metachronal order quality

indistinguishable wave states
Kanale, Ling, Fuerthauer, Kanso, (2022)
Kuramoto order and a continuum theory



Scalar Kuramoto order parameter cannot distinguish metachronally ordered states:
- coarse-graining local Kuramoto order parameter for a continuum theory
- project into angular variable for wave characteristics (Radon transform)
- eccentricity symbolizes metachronal order quality

indistinguishable wave states
Kanale, Ling, Fuerthauer, Kanso, (2022)
One model to rule them all?
Data-driven parameters?

⤸
⤸
⤻
⤻
Nawroth, Ling, et al. (unpublished)
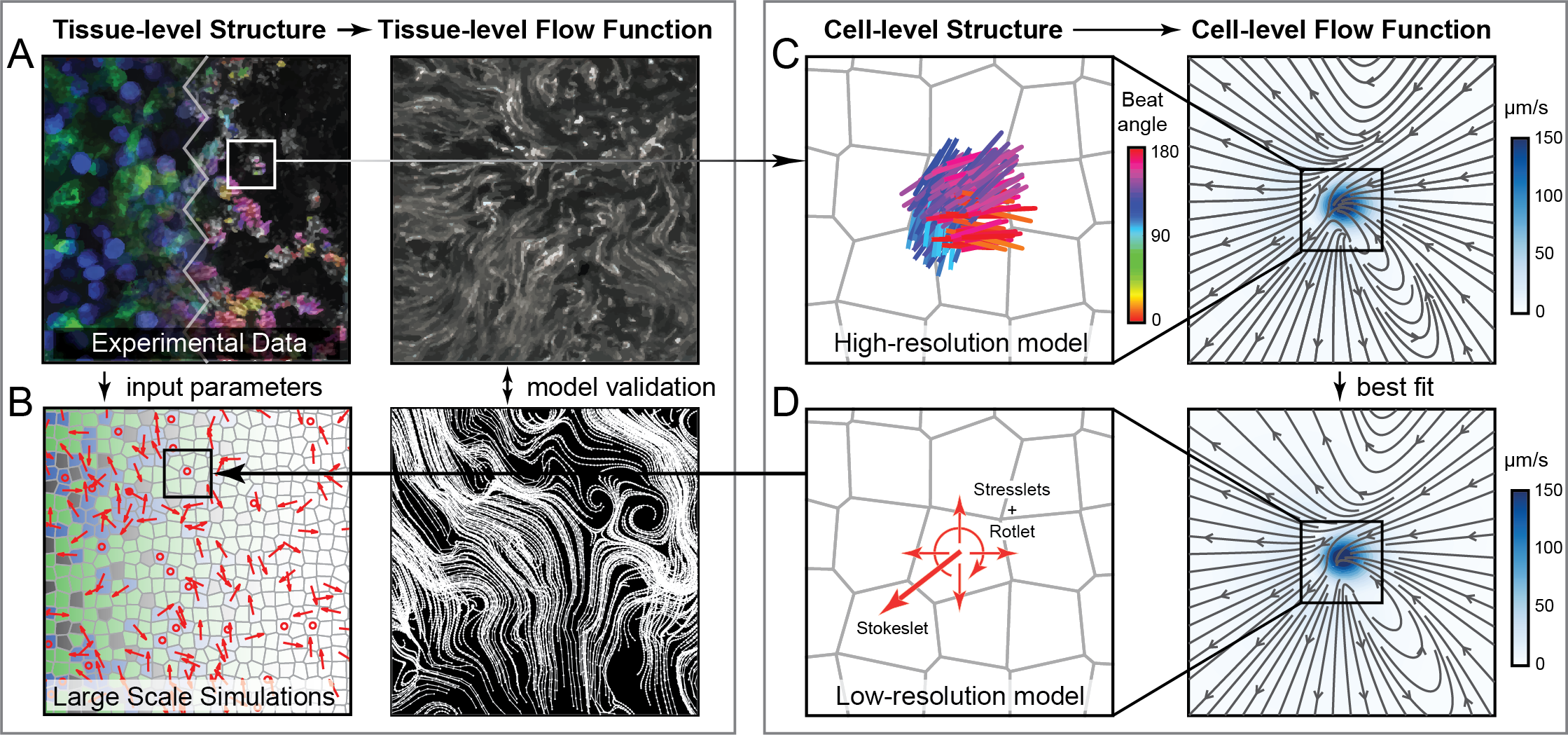
structure
flow function
\(\downarrow\) input
\(\updownarrow\) validate/predict
Measurements
Theory/Models
End-to-end cilia modeling
-
motor-driven, filament-derived phased oscillators and continuum theory
-
data-driven cilium- and tissue- level parameters
-
complex fluids / multi-physics
-
validation & prediction of tissue-level functions
Thank you!




NIH R01 Grant 1R01HL153622-01A1
NSF INSPIRE Grant 1608744
ONR Grant N00014-17-1-2062
ARO Grant W911NF-16-1-0074

Janna Nawroth
USC / Helmholtz Pioneer Campus

PI: Eva Kanso

Hanliang Guo
University of Michigan

Sebastian Fürthauer
Flatiron / TU Wien

Yi Man
USC / Peking University

Anup Kanale
USC / Medtronics