三角函數
Lecturer: 立葉
建北電資小設課運算思維 Lesson 3
~~啊你們怎麼國中就有學到了~~
先來講講基本定義和一些雜七雜八!
最基礎的定義...?
\(\sin \theta = \frac{a}{c}\)
\(\cot \theta = \frac{b}{a}\)
\(\csc \theta = \frac{c}{a}\)
\(\sec \theta = \frac{c}{b}\)
\(\tan \theta = \frac{a}{b}\)
\(\cos \theta = \frac{b}{c}\)
特殊三角比
30-60-90三角形
45-45-90三角形
\(\sin 15\degree = \frac{\sqrt{6}-\sqrt{2}}{4}\)
| 角度比 | 30-60-90三角形 | 45-45-90三角形 |
|---|---|---|
| 邊長比 |
\(1:\sqrt{3}:2\)
\(1:1:\sqrt{2}\)
\(\cos 18\degree = \frac{\sqrt{5}-1}{4}\)
倒數關係
\(\sin \theta\csc \theta = 1\)
\(\tan \theta \cot \theta = 1\)
\(\cos \theta\sec \theta = 1\)
商數關係
\(\frac{\sin \theta}{\cos \theta} = \tan \theta\)
\(\frac{\cos \theta}{\sin \theta} = \cot \theta\)
\(\frac{\sec \theta}{\csc \theta} = \tan \theta\)
\(\frac{\csc \theta}{\sec \theta} = \cot \theta\)
三角恆等式
\(\sin^2 \theta + \cos^2 \theta = 1\)
\(\tan^2 \theta + 1 = \sec^2 \theta\)
\(1 + \cot^2 \theta = \csc^2 \theta\)
超級六角形

小小的例題
\(8\)
求這個三角形中\(\sin\theta, \cos\theta, \tan\theta\)
\(10\)

A: \(\sin\theta = \frac{4}{5} \\ \cos\theta = \frac{3}{5} \\ \tan\theta = \frac{4}{3}\)
再回到剛剛的三角形
\(\sin \theta = \frac{a}{c}\)
\(\cos \theta = \frac{b}{c}\)
由此可推知
\(a = c\sin \theta\)
\(b = c\cos \theta\)
投影定理
A: \(a\cos\alpha + b\cos\beta \)
請以\(a, b, \alpha, \beta\)表示\(c\)。

三角函數的幾何意義
此圓為單位圓。請試著找出可以分別代表\(\sin \theta, \cos\theta, \tan\theta,\\ \cot\theta, \sec\theta, \csc\theta\)
的線段。
\(C\)
\(B\)
\(A\)
\(D\)
\(A\)
\(F\)
\(G\)
\(O\)

\(|\sec\theta|>|\tan\theta|>|\sin\theta|\)
\(|\csc\theta|>|\cot\theta|>|\cos\theta|\)
小小的例題
A: \(a\cos\theta\sin\theta\)
請以\(a, \theta\)表示\(d\)。

始邊終邊廣義角
廣義角:\(\theta \in \real \)
以逆時針為正向

\(\overrightarrow{OA}\):始邊
\(\overrightarrow{OB}\):終邊
\(\tan\theta\) 在 \(\theta = \frac{\pi}{2} + k\pi, k \in \text{Z}\)
時沒有意義
標準位置角
終邊落在第n象限,則稱其為第n象限角
若落在\(x\)或\(y\)軸上,則稱其為象限角
始邊在\(x\)軸正向上!
\(\sin\theta\)新ㄉ定義:圓點為圓心ㄉ單位圓與終邊交點的
\(y\)座標
\(\cos\theta\)新ㄉ定義:
\(x\)座標
\(\tan\theta\):\(\frac{y}{x}\),
在\(x\)為零的時候無意義
角度轉換
原函數不變
正餘互換
| 原函數 | sin | cos | tan | |
|---|---|---|---|---|
| 化成的函數 (正負視象限而定) |
sin | cos | tan |
\((180\degree \pm \theta), (360\degree \pm \theta)\)
\(\theta\)
| 原函數 | sin | cos | |
|---|---|---|---|
| 化成的函數 (正負視象限而定) |
cos | sin |
\((90\degree \pm \theta), (270\degree \pm \theta)\)
\(\theta\)
角度轉換
請求出以下的三角函數值?
\(\sin 150\degree\)
\(\cos 135\degree\)
\(\tan 225\degree\)
\(\sin -60\degree\)
\(\cos 180\degree\)
\(\tan -300\degree\)
\(\sin 1050\degree\)
\(\cos 0\degree\)
\(\tan 450\degree\)
正弦定理 && 餘弦定理
正弦定理
\(\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R\)
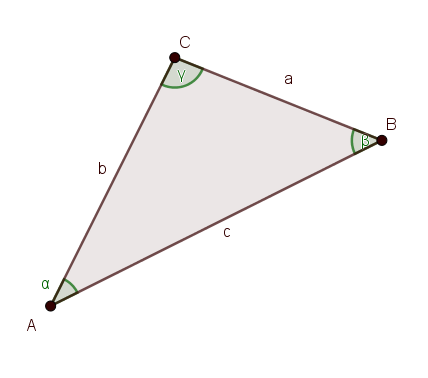
三角形面積
\( = \frac{1}{2} \overline{AB} \cdot \overline{AC} \cdot \sin A \)

\( = \frac{1}{2} \overline{BC} \cdot \overline{BA} \cdot \sin B \)
\( = \frac{1}{2} \overline{AC} \cdot \overline{BC} \cdot \sin C \)
面積
海龍公式
設 \(a, b, c\)為三角形的三邊長
\(s = \frac{a+b+c}{2}\)
則此三角形面積為
\(\sqrt{s(s-a)(s-b)(s-c)}\)
餘弦定理
\( c^2 = a^2 + b^2 + 2ab\cos\text{C}\)

弧度量
弧度量
\(\pi \text{ rad} = 180\degree\)
\(1 \text{ rad} \approx 57.32 \degree\)

三角函數的一堆公式。
吐了
ㄛ還有疊合啦哈哈
合腳攻勢和角公式
由上一頁的證明,我們可以推出以下幾個式子:
\(\cos(a+b) = \cos a\cos b-\sin a\sin b\)
\(\cos(a-b) = \cos a\cos b+\sin a\sin b\)
\(\sin(a+b) = \sin a\cos b+\cos a\sin b\)
\(\sin(a-b) = \sin a\cos b-\cos a\sin b\)
\(\tan(a+b) = \frac{\tan a+\tan b}{1-\tan a\tan b}\)
\(\tan(a-b) = \frac{\tan a-\tan b}{1+\tan a\tan b}\)
倍角公式
由上一頁的證明,我們可以推出以下幾個式子:
\(\cos 2\theta = \cos^2 \theta- \sin^2 \theta\\ = cos^2 - (1 - \cos^2 \theta) \\ = 2\cos^2 \theta - 1 \\ = 1 - 2\sin^2 \theta\)
\(\sin 2\theta = \sin\theta\cos\theta + \cos\theta\sin\theta \\ = 2\sin\theta\cos\theta\)
倍角公式
\(\tan 2\theta = \frac{2\tan\theta}{1-\tan^2\theta}\)
\(2\tan\theta, \dotsb, 1-\tan^2\theta, 1+\tan^2\theta\)
\(\sin 2\theta = \frac{2\tan\theta}{1+\tan^2\theta}\)
\(tan 2\theta = \frac{1-\tan^2\theta}{1-\tan^2\theta}\)
\(\sin \frac{\theta}{2} = \pm \sqrt{\frac{1-\cos\theta}{2}}\)
半角公式
\(\cos \frac{\theta}{2} = \pm \sqrt{\frac{1+\cos\theta}{2}}\)
\(\tan \frac{\theta}{2} = \pm \sqrt{\frac{1-\cos\theta}{1+\cos\theta}} = \frac{1-\cos\theta}{\sin\theta} = \frac{\sin\theta}{1+\cos\theta}\)
三角函數的圖形
三角函數的圖形

\(y = \sin x\)
奇函數

週期:\(2\pi\)
對稱於原點
\(y = \cos x\)
偶函數
週期:\(2\pi\)
對稱於\(y\)軸
三角函數的圖形
\(y = \sin x\)
奇函數
週期:\(2\pi\)
定義域:\(x \in \real\)
值域:\(y \in \{-1, 1\}\)

三角函數的圖形
\(y = \cos x\)
偶函數
週期:\(2\pi\)
定義域:\(x \in \real\)
值域:\(y \in \{-1, 1\}\)

三角函數的圖形
\(y = \tan x\)
奇函數
週期:\(\pi\)
定義域:\(x \in \real \cup x \neq \frac{\pi}{2}+k\pi, k \in \real\)

值域:\(y \in \real\)
三角函數圖形的疊合
今天我們知道
\(-1\leq \sin\theta \leq 1\)
\(-1 \leq \cos\theta \leq 1\)
那 \(\sin\theta + \cos\theta\) 呢?
今天我們知道
\(-1\leq \sin\theta \leq 1\)
\(-1 \leq \cos\theta \leq 1\)
\(\sqrt{2}(\frac{1}{\sqrt{2}} \sin\theta + \frac{1}{\sqrt{2}} \cos\theta)\)
\(\sqrt{2}\sin(\theta+\frac{\pi}{4})\)