Mais qui est donc l'inventeur de la BlockChain ?


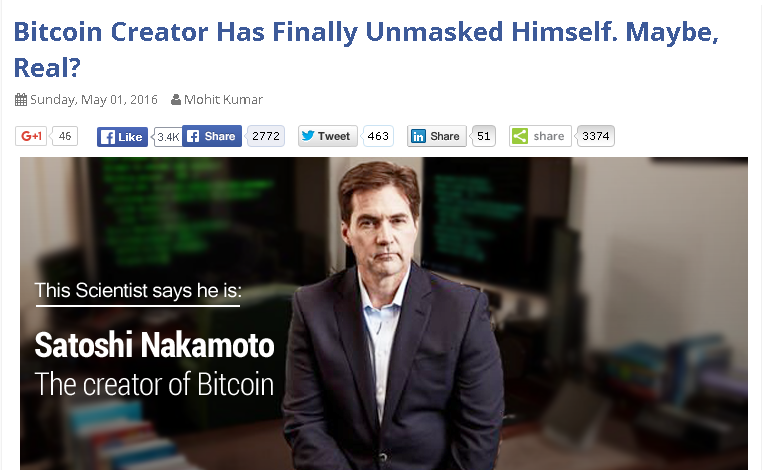

[8],[6],[4]
La communauté est réticente...


[1],[2],[3],[4]


[9]
Explications de la supercherie
- Craig Wright poste sur son blog (l'article a disparu) une signature d'un message qu'il aurait fait avec une des clés privées de Nakamoto Satoshi. (base64)
MEUCIQDBKn1Uly8m0UyzETObUSL4wYdBfd4ejvtoQfVcNCIK4AIgZmMsXNQWHvo6KDd2Tu6euEl13VTC3ihl6XUlhcU+fM4=
2. Transformer en hexadecimal cela donne
3045022100c12a7d54972f26d14cb311339b5122f8c187417dde1e8efb6841f55c34220ae0022066632c5cd4161efa3a2837764eee9eb84975dd54c2de2865e9752585c53e7cce
3. Signature que l'on retrouve dans la BlockChain..

[7]
Explications de la supercherie
Algorithme de signature d'une transaction Bitcoin et d'un message :
- secp256k1(sha256(sha256(transaction)))
- secp256k1(sha256(sha256(message)))
Même algorithme = duperies de Craig Wright.
Celui ci ne nous montre pas le prétendu message car supposé trop long, il nous donne seulement le hash de celui ci.
Il est allé cherché dans la BlockChain une transaction de Satoshi inconnu, qui contient une signature d'une transaction.
Il a recalculé le Hash de cette transaction, et a prétendu que son fichier avait le même hash...
Quelques liens
-
La cryptographie, discipline mathématique
-
Le problème de la signature des noms de domaine
-
Comment la BlockChain propose un remède à ce problème ?
-
Le PageRank comme solution contre les "squatters"
-
Implémentation
-
Test et Questions
-
Bibliograhie

Plan
1/ La cryptographie,
domaine mathématique

Origine de la cryptographie
- Communiquer en toute sécurité
- Origine grecque "kruptos" = caché et "graphein" = écriture.
- Début au X ème siècle avant J.C : utilisation de la Scytale .
- V ème siècle avant J.C chez les Hébreux : chiffrement Atbash
- I er siècle avant J.C : chiffrement monoalphabétique ( César )



Le cryptosystème RSA
- Le plus utilisé
- cryptage asymétrique ( à clé publique )
- problème de factorisation d'entiers
- générations de grands nombres premiers

Attaquer RSA
- Module commun + Démonstration
- petit exposant privé + Démonstration
- Attaque par "broadcast" + Démonstration
Test de primalité : Test de Miller Rabin


Permet de savoir pour p et q très grands s'ils sont premiers.
Principe général de Miller Rabin
- On choisit a au hasard (a < n )
- On calcule a^t mod n => Si on trouve 1 alors a n'est pas un témoin de miller pour n .
- Sinon, on calcule a^[2^i]*t et si pour un certain i , on trouve -1 alors a n'est pas un témoin de miller pour n.
- Si pour k valeurs aléatoires de a, aucune n'est témoin de miller alors n est vraisemblablement premier.
2/ Le problème de la signature des noms de domaine




Principe de fonctionnement d'une autorité de certificat
Le certificat S peut être générée avec des clés RSA
S^e = Message % n
// e : exposant publique (souvent 65537)
// n : le module de la clé publique[3]
Analyse d'une connection HTTPS avec le logiciel WireShark

[1],[2]
Les problèmes liés à un tel système d'autorité de certificat :
-
Confiance absolu dans l'autorité
-
Certificat pré installé par le navigateur, imposé à l'utilisateur
La BlockChain
- Issu de la cryptomonnaie Bitcoin
- Une chaîne de blocs (en anglais : blockchain) est une base de données distribuée qui gère une liste d'enregistrements protégés contre la falsification ou la modification par les nœuds de stockage

... Nous prendrons comme exemple la chaine de bloc du réseau Bitcoin
Qu'est ce qu'un Bloc ?
Un Bloc est composé de
- un ensemble de transactions que le Bloc vérifie
- un en tête l'identifiant de manière unique
- la version de la BlockChain
- un hash l'identifiant de manière unique
- un hash identifant le précédent Bloc
- un arbre de Merkle
- un temps
- un nonce
- un niveau de difficulté

[1]
Un arbre de Merkle
Un arbre de hachage est une structure de données contenant un résumé d'information d'un volume de données, généralement grand
Arbre de Merkle pour un nombre de transactions impaires


Leur utilisation dans la crypto monnaie
permet à certains noeuds du réseau
de ne pas maintenir une copie complète de la BlockChain en locale, on appelle cela
Simplified Payment Verification
[2]
La construction d'un arbre de Merkle
void Block::BuildMerkleRoot()
{
// To get a even number of transactions
if (transactions.size() & 1) {
transactions.push_back(transactions.at(transactions.size() - 1)); nombreTransaction++;
}
int N = transactions.size();
vector<string> hashTree;
hashTree.resize(2 * N - 1);
for (int i = 0; i < N; i++)
hashTree.at(2 * N - 2 - i) = transactions.at(i);
for (int i = N - 2; i > -1; i--)
{
hashTree.at(i) = SHA25::sha256(SHA25::sha256(hashTree.at(2 * i + 1) + hashTree.at(2 * i + 2)));
}
header.setHashMerkleRoot(hashTree.at(0));
header.setTime(boost::posix_time::second_clock::local_time());
blockHash = SHA25::sha256(SHA25::sha256(header.get_HashMerkleRoot()));
}Miner la BlockChain
- Seulement une partie du réseau Bitcoin mine la BlockChain
- Sans minage, pas de chaîne de bloc sûr
- Miner, c'est résoudre une preuve de travail :
Trouver un nonce n pour un Bloc B pour une difficulté X tel que : SHA256(SHA256(headerHash(B) + n)) < 0.(X zeros)..01000000

int Block::solveProofofWork(bool& stop)
{
unsigned long long nonce = 0;
unsigned long long const limit = std::numeric_limits<unsigned long long>::max();
string sol(Constante::DIFFICULTY_MINING, '0');
while (true) {
string hash = SHA25::sha256(SHA25::sha256(
string(header.get_HashMerkleRoot() +
std::to_string(nonce))));
if (hash.substr(0, Constante::DIFFICULTY_MINING) == sol)
break;
else
++nonce;
}
header.setNonce(nonce);
return nonce;
}- Le nombre de zéros est actuellement de 13, ce qui équivaut en moyenne à 10 minutes de recherche pour des supercalculateurs optimisés et une éternité pour un simple ordinateur
- Toutes les 2000 blocs environ, ce nombre est recalculé
- Complexité exponentielle en difficulté. Il y a ~1 000 000 000 000 000 000 000 000 de hash à calculer.
- Un mineur avec une capacité de calcul de 1 trillions de hash par secondes mettrait 59 jours en moyenne pour résoudre le POF
Chiffres et Code
Utilité
-
Impossibilité de forger des faux blocs.
- Un Bloc est correct si il a une référence sur un autre bloc déjà miné. Il est cependant peu probable de trouver le nonce plusieurs fois avant tout le monde. Pour cela il faudrait posséder au moins 50 % du réseau de minage.
- Solution complètement aléatoire.
- Il est impossible de trouver le message en connaissant son hash.
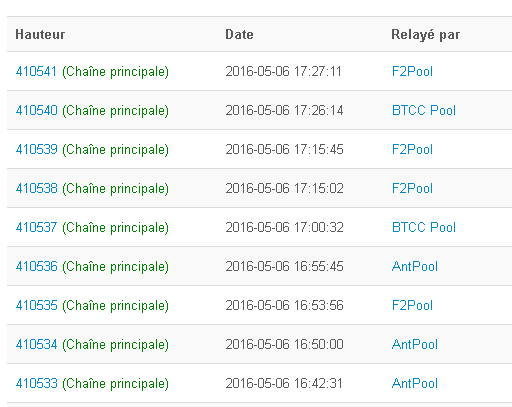
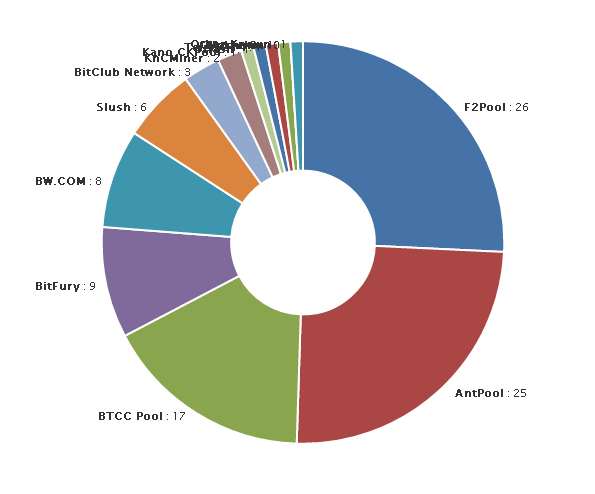
Distribution du HashRate et resultat du minage des blocs de 410533 à 410541
Les Forks 1
1. Un fork apparaît lorsque deux mineurs résolvent la preuve de travail en même temps !
2. Ils partagent leur nonce trouvé avec le réseau. Chaque noeud recevant le nouveau Bloc le vérifie avant de l'ajouter dans sa BlockChain
3. Le réseau est coupé en deux puisque les deux blocs se propagent à une vitesse différente
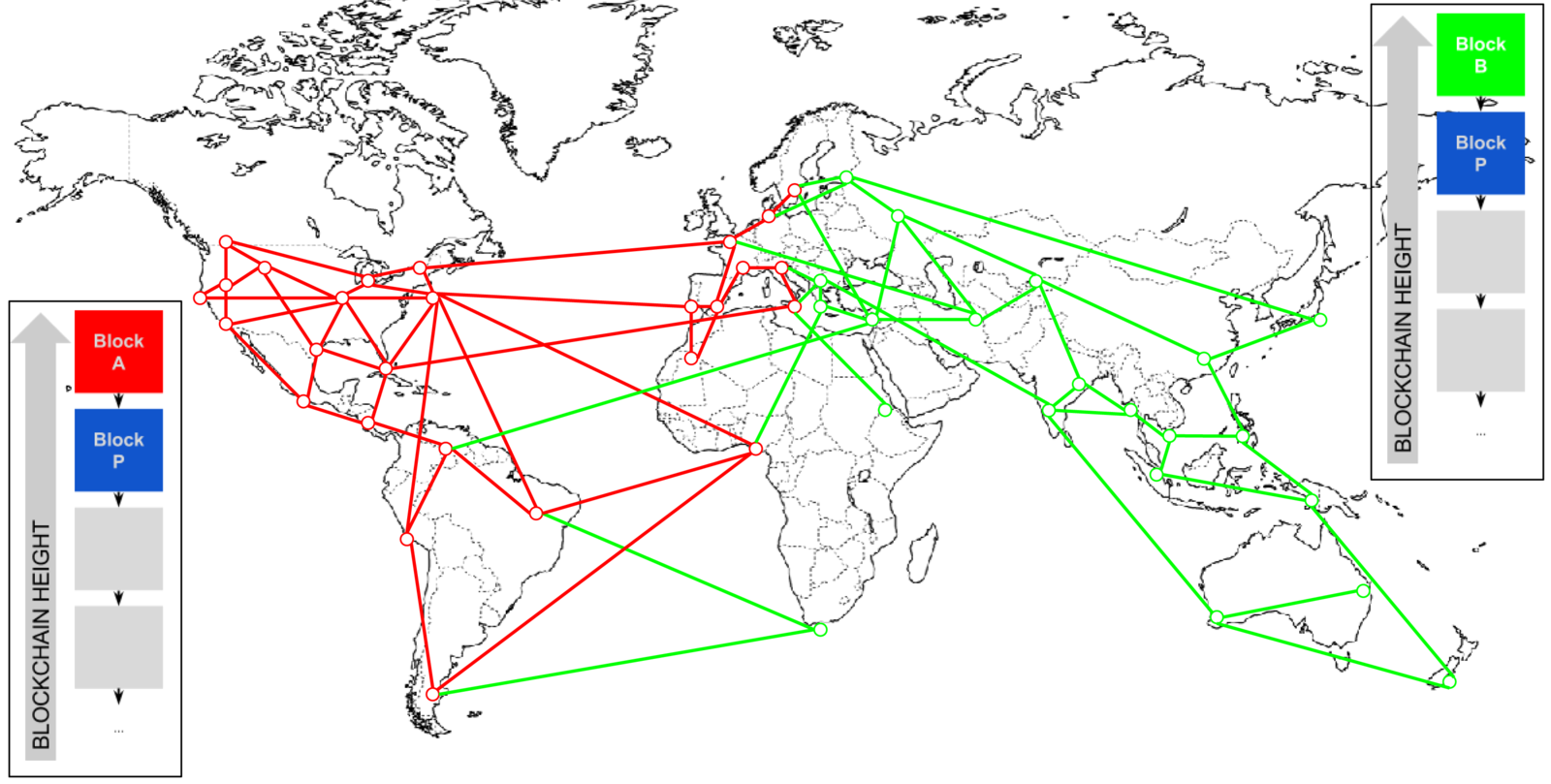
Les Forks 2
4. Une partie des mineurs vont miner "au dessus" du bloc vert, et l'autre au dessus du bloc rouge.

Conclusion :Comme les mineurs minent toujours au dessus de la plus longue chaîne, alors un consensus commun s'établit au delà d'une certaine profondeur
5. Un nouveau bloc a été trouvé chez les "verts". Les noeuds minant le bloc rouge vont recevoir un bloc qui a été miné sur le bloc vert, ils vont donc suspendre leur bloc miné, et passer sur la plus haute chaine de bloc
La BlockChain pour les noms de Domaine
- Permet d'enregistrer les noms de domaine dans une base de donnée. Chaque information est certifiée par la BlockChain. Il ne peut y avoir des doublons.
- Possibilité de s'échanger des emplacement pour un nom de domaine
- Eviter la censure
- Décentraliser un peu plus des autorités inutiles

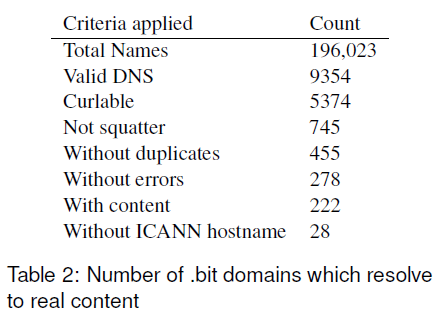
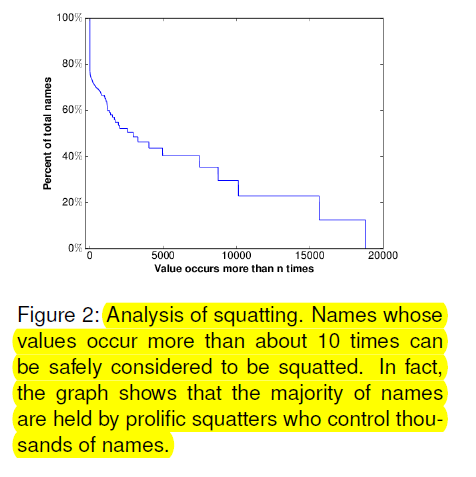
Une réflexion sur le problème des squatters
[3]
PageRank
Idée pour le problème précédent: Affecter à chaque page un prix fonction de son PageRank pour repousser les squatteurs de noms de domaine populaire

Idée de PageRank : Une page est d'autant importante que d'autres pages importantes ont des liens vers elle
Principe de l'algorithme
Calculer une matrice H creuse. Puis à l'aide de la méthode de la puissance itérée, trouvez un vecteur r tel que
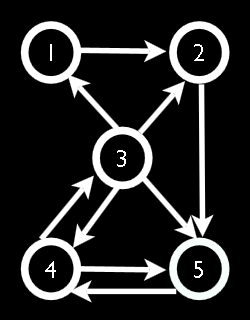
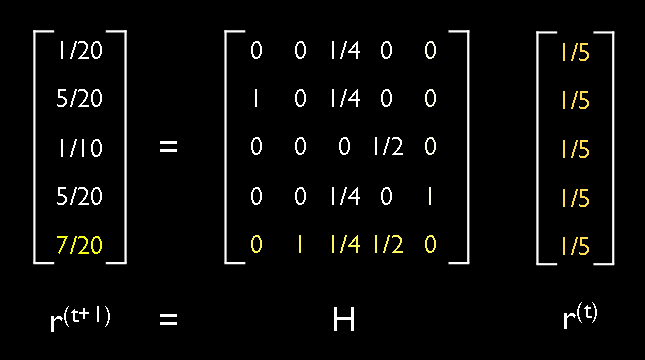
De plus la matrice H peut être vu comme une matrice de transition d'une chaine de Markov. Ainsi pour que la méthode de la puissance itérée converge, il faut que la la matrice H soit stochastique, apériodique, et irréductible
Solution 1
Exemple !


Propriétés de cette matrice :
- Somme éléments colonne = 1
- Eléments positifs ou nuls
Matrice de transition d'une chaîne de Markov !

Xn : Variable aléatoire à valeurs dans E après n étapes.
E : Espace d'état {A,B,C,D,E}
Probabilité indépendante de n : chaîne de markov sans mémoire !

Probabilité d'être à la page i, sachant que l'on était à la page j après deux étapes (Démonstration)

Probabilité d'être sur une page est indépendante du point de départ ( ici n>32 ) !


La ième coordonnée de ce vecteur = la probabilité d'être sur la page i à l'instant n
- La probabilité d'être à la page i à l'instant n+1 : loi stationnaire
- Permet d'ordonner les pages : {B,A,C,E,D}

Problèmes :
- 1 peut être une valeur multiple du polynôme caractéristique
- La matrice P peut avoir différentes valeurs propres différentes de 1 , de module égal à 1.
Une matrice P sans problèmes est dite régulière
Résolution du problème :
Matrice P non régulière ? Déformons la !


Implémentation
-
Première solution naive : Calculer H
- Problème de stockage
-
Deuxième solution : ne garder que deux vecteurs : les arcs entrants et les arcs sortants de tous les nœuds du graphe, et recalculé à chaque fois le score de la matrice H pour toutes ses composantes
- Problème de temps
-
Troisième solution: Comme beaucoup de calculs sont similaires, regrouper pour chaque ligne toutes les colonnes qui ont la même valeur
- Fonctionnel en temps correct pour des gros graphes (~1 M de nœuds)
while (!stop)
{
nombre_iteration++;
j = 0;
long float sum2 = 0;
long float sum3 = 0;
auto end = outgoing_link_null.end();
i = 0;
std::for_each(PR.begin(), PR.end(), [&sum2,&end,&i,&outgoing_link_null,&sum3](const auto& n) {
sum2 += n;
if (outgoing_link_null.find(i) != end)
sum3 += n;
i++;
});
for (i = 0; i < N; i++)
{
res = 0;
std::for_each(in_degree.at(i).begin(), in_degree.at(i).end(), [&res,&PR,&out_degree](const auto& x) {
res += alpha*(1 / static_cast<long float>(out_degree.at(x).size()))* PR.at(x);
});
res += (alpha / static_cast<long float>(N))*sum3;
res += sum2*coeff2;
buffer.at(i) = res;
}
i = 0;
for (const auto& x : buffer)
{
if (std::abs(x - PR.at(i++)) > convergence)
{
PR = buffer;
break;
}
if (i == N)
stop = true;
}
}Test de la BlockChain implémenté
Bibliographie
- Introduction
- [1] https://www.reddit.com/r/Bitcoin/comments/4hflr3/craig_wrights_signature_is_worthless/
- [2] http://blog.erratasec.com/2016/05/satoshi-how-craig-wrights-deception.html#.Vy0pdOQwK01
- [3] https://rya.nc/sartre.html
- [4] http://gavinandresen.ninja/
- [5] https://dankaminsky.com/
- [6] http://www.bbc.co.uk/news/technology-36193006
- [7] https://blockchain.info/fr
- [8] http://thehackernews.com/2016/05/craig-wright-bitcoin.html
- [9] http://www.drcraigwright.net/
- Mathématique
Bibliographie
- Autorité de certificat
- BlockChain
- PageRank