Beyond Independence: Advances in Network Inference via Gaussian Graphical Models for Multimodal Data

Luisa Cutillo, l.cutillo@leeds.ac.uk, University of Leeds

in collaboration with

Bailey Andrew, and David Westhead, UoL

Sections

  • Recap: Gaussian Graphical models and GmGM
  • New: Non Central GmGM
  • New: Strong Product Model

Part 1

Background on Gaussian Graphical Models (GGM) and GmGM

Biological Networks

Examples:

  • Genetic interaction networks
  • Metabolic networks
  • Signalling networks
  • Gene regulatory networks
  • Protein-protein interaction networks

Gaussian graphical model (GGM) estimation is one approach to estimating biological networks

undirected graphical model

X=(X_1,\ldots,X_p)

X1

X3

X2

X4

X5

X6

X7

X8

As

G(V,E)

Vertices V

Edges E 

A_{i,j} \neq 0
X_1
X_3
X_5
X_2
X_4

Global Markov Property: 

X_A {\mathrel{\perp\!\!\!\perp}} X_B | X_C

conditional independence graph 

the absence of an edge between nodes in A and in B corresponds to conditional independence of the random vectors A, B given the separating set C

X=(X_1,\ldots,X_5)
X_1
X_2
X_3
X_4
X_5

What is a GGM?

special case of conditional independence graph where  

\Theta=\Sigma^{-1}\in R^{p\times p}
X=(X_1,\ldots,X_p)\sim MVN(\mu, \Sigma)

Edges weights E ∝ Precision matrix

Vertices V

f_x(x_1,\ldots,x_p)\propto exp \left(\frac{(x-\mu)^T\Sigma^{-1}(x-\mu)}{2}\right)

Partial correlations via                                   

partial correlation

\Theta= (\theta_{ij})=\Sigma^{-1}
pcor(i,j)=-\frac{\theta_{i,j}}{\sqrt{\theta_{ii}\theta_{jj}}}

(Dempster, 72) it encodes the conditional independence structure

X_i {\mathrel{\perp\!\!\!\perp}} X_j | X_{-i,-j} \leftrightarrow pcor(i,j)=0

The sparsity pattern of Θ expresses conditional independence relations encoded in the corresponding GGM

Estimating ~ \Theta= (p_{ij})=\Sigma^{-1}
0.894
-0.707
correlations: \left[\begin{array}{lll} \sigma{11}=1 & \sigma{12}=0.894 & \sigma{13}=-0.707\\ \sigma{21}=0.894 & \sigma{22}=1 & \sigma{23}=-0.632\\ \sigma{31}=-0.707 & \sigma{32}=-0.632 & \sigma{33}=1\\ \end{array}\right]
\rho_{i,j}=pcor(i,j)=-\frac{\theta_{i,j}}{\sqrt{\theta_{ii}\theta_{jj}}}
part. \ corr.: \left[\begin{array}{lll} \rho{11}=1 & \rho{12}=0.816 & \rho{13}= -0.408\\ \rho{21}=0.816 & \rho{22}=1 & \rho{23}=0\\ \rho{31}= -0.408 & \rho{32}=0 & \rho{33}=1 \\ \end{array}\right]

Conditional Independence = SPARSITY!

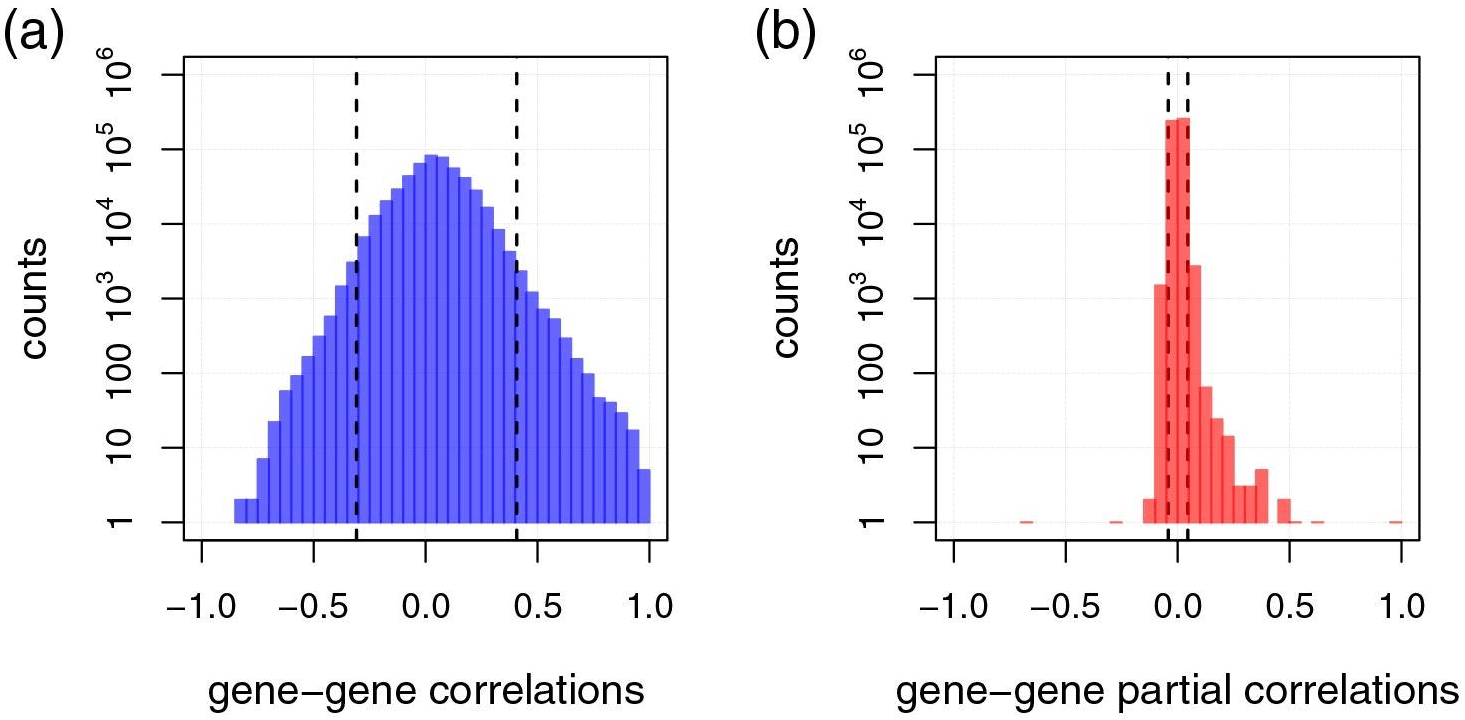
GGMs Networks VS Correlation Networks

Shutta et al 2022 GGM with appl. to omics analysis

Genes 1, 2, 3 

X=(X_1,X2,X_3), e=(e_1,e_2,e_3)\sim_{iid} N(0,1)
X_1=3+e_1, ~ ~X_2=2X_1+e_2, ~ ~ X_3=-X_1+e_3
X_3
X_1
X_2
-0.632
0.816
-0.408
X_3
X_1
X_2

GGMs Networks VS  Correlation Networks

IEstimated gene-gene Pearson correlation coefficients (a) with their respective full order partial correlation coefficients (b) for single-cell RNA sequencing data of melanoma metastases (Tirosh et al., 2016).

Michael Altenbuchinger et al. Gaussian and Mixed Graphical Models as (multi-)omics data analysis tool

About Sparsity...

  • We want to study GGMs where        is sparse
  • This means more conditional independent variables
  • Fewer elements to estimate -> Fewer data needed

Sparsity assumption => max graph degree d<<p

 is reasonable in many contexts!

 

Example: Gene interaction networks

\Theta

About Sparsity...

 

However the " Bet on Sparsity principle" introduced Tibshirani 2001, "In praise of sparsity and convexity":

(...no procedure does well in dense problems!)

  • How to ensure sparsity?

Graphical Lasso (Friedman, Hastie, Tibshirani 2008):

imposes an       penalty for the estimation of 

\Theta= \Sigma^{-1}
max_{\Theta>0} \left[ log(det(\Theta))-tr(S\Theta) + \lambda \lVert \Theta \rVert_1 \right]
L_1

Limitation

  • Assumption of independence between features and samples
  • Finds graph only between features

Features

Samples

Data

Single cell data

extract the conditional independence structure between genes and cells,  inferring a network both at genes level and at cells level.​

Cells

Genes

 2  ... 10
  :  ...   :
 5  ...  7

Graph estimation without independence assumption

 

We need a general framework that models conditional independence relationships between features and data points together.

Bigraphical lasso: A different point of view

(Kalaitzis et al. (2013))

 

 

Preserves the matrix structure by using a  Kronecker sum (KS) for the precision matrixes

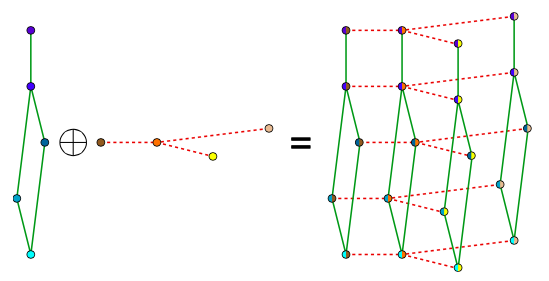
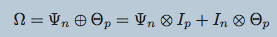
KS => Cartesian product of graphs' adjacency matrix

(eg. Frames x Pixels)

Bigraphical lasso: A different point of view

(Kalaitzis et al. (2013))

 

 

Limitations:

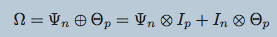
  • Space complexity: There are                     dependencies but actually implemented to store                   elements
O(n^2 + p^2)
O(n^2p^2)
  • Computational time: Very slow, could only handle low hundreds samples.
  • Exploits eigenvalue decompositions of the Cartesian product graph and a more efficient version of the algorithm
  • Reduces memory requirements from O(n^2p^2) to O(n^2+ p^2).
  • Replaces Gaussianity with weaker  ‘Gaussian copula’ assumption through preprocessing tools non-paranormal skeptic
  • Introduces matrix non-paranormal distribution with a Kronecker sum structure
  • Can be used on data with arbitrary marginals, as long as relationships between the datapoints ‘behave Gaussianly’).

https://github.com/luisacutillo78/Scalable_Bigraphical_Lasso.git

Two-way Sparse Network Inference for Count Data
S. Li, M. Lopez-Garcia, N. D. Lawrence and L. Cutillo (AISTAT 2022)

 

  • TeraLasso (Greenewald et al., 2019), EiGLasso (Yoon & Kim, 2020) better space and time complexity (~scLasso)
  • Can run on low thousands in a reasonable amount of time

 

Related work for scalability

Limitations of prior work

  • Not scalable to millions of features

  • Iterative algorithms

  • Use an eigendecomposition every iteration (O(n^3) runtime - > slow)

  • O(n^2) memory usage

Do we need to scale to Millions of samples?

What is the improvement in GmGM?

In previous work graphical models an L1 penalty is included  to enforce sparsity

  • Iterative algorithms

  • Use an eigendecomposition every iteration (O(n^3) runtime-slow!)

If we remove the regularization, we need only 1 eigendecomposition!

In place of regularization, use thresholding

Our Approach: GmGM

Part 2

https://github.com/BaileyAndrew/GmGM-python

  • A metagenomics matrix of 1000 people x 2000 species
  • A metabolomics matrix of 1000 people x 200 metabolites

We may be interested in graph representations of the people, species, and metabolites.

GmGm addresses this problem!

GmGM: a fast Multi-Axis Gaussian Graphical Model ongoing PhD project (Andrew Bailey), AISTAT 2024

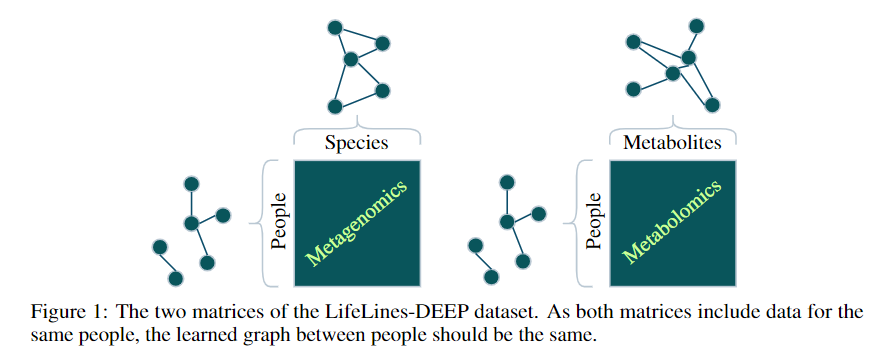
\begin{align*} \mathcal{D}^\gamma \sim \mathcal{N}\left(\mathbf{0}, \left(\bigoplus_{\ell\in\gamma}\mathbf{\Psi}_\ell\right)^{-1}\right) &\iff \mathcal{D}^\gamma \sim \mathcal{N}_{KS}\left(\left\{\Psi_\ell\right\}_{\ell\in\gamma}\right) \end{align*}

Tensors (i.e. modalities) sharing an axis will be drawn independently from a Kronecker-sum normal distribution  and parameterized by the same precision matrix

\begin{align*} \mathbf{D}^\mathrm{metagenomics} \sim& \mathcal{N}_{KS}\left(\mathbf{\Psi}^\mathrm{people}, \mathbf{\Psi}^\mathrm{species}\right) \\ \mathbf{D}^\mathrm{metabolomics} \sim& \mathcal{N}_{KS}\left(\mathbf{\Psi}^\mathrm{people}, \mathbf{\Psi}^\mathrm{metabolites}\right)% \\ %&\text{(independently)} \end{align*}

Additional Assumptions!

  • Both input datasets and precision matrices can be approximated by low-rank versions

Still some limitations:

  •  the initial eigen-decomposition is O(N^3) per axes anyway
  • this can be unfeasible for large and complex datasets
  • O(pn) memory
  • O(pn^2) runtime

 

Is our GmGM  much faster / good enough?

Is our GmGM  much faster / good enough?

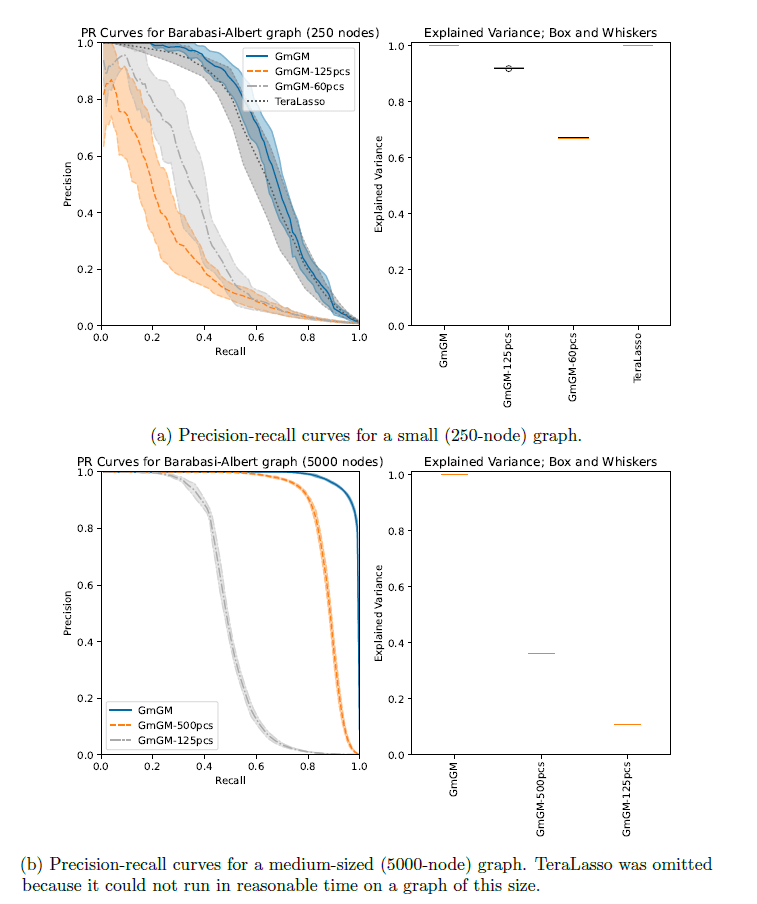
Part 2

Non Central GmGM

2025

https://github.com/BaileyAndrew/Noncentral-KS-Normal 

What’s the Problem with Uncentered Data?

In multi-axis case, inference is usually done in a one sample scenario

Zero mean assumption

can cause egregious modelling errors!

We relax the zero-mean assumption

we propose the
“Kronecker-sum-structured mean”

model with likelihood that
can be solved efficiently with coordinate descent.

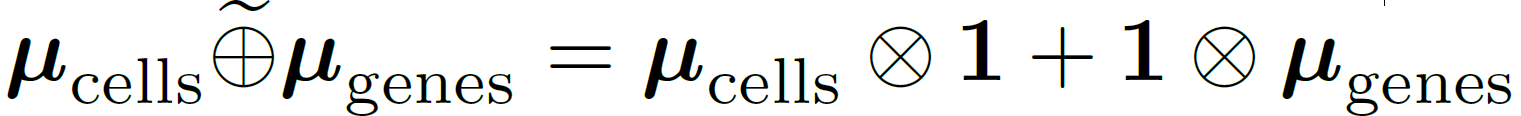
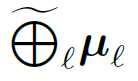
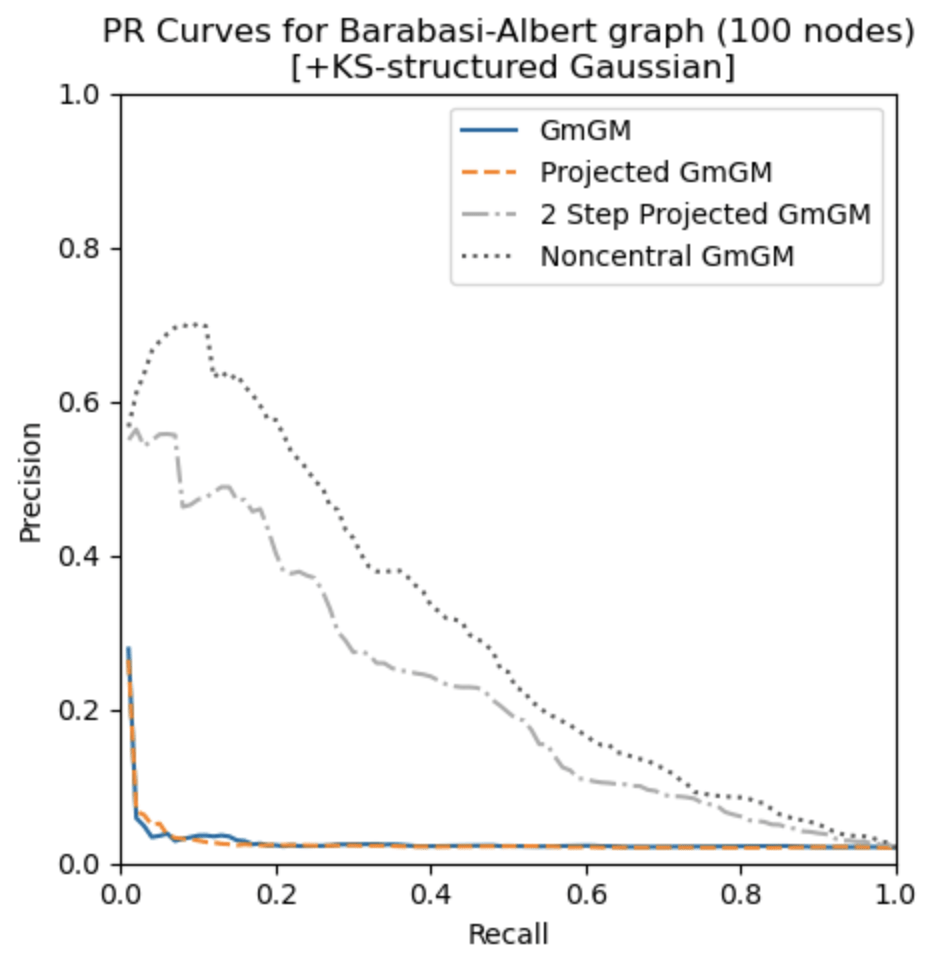
Remarks

 

  • noncentral GmGM is a ‘drop-in wrapper’ for pre-existing methods!

 

  • Our estimator for the parameters is the global maximum likelihood estimator

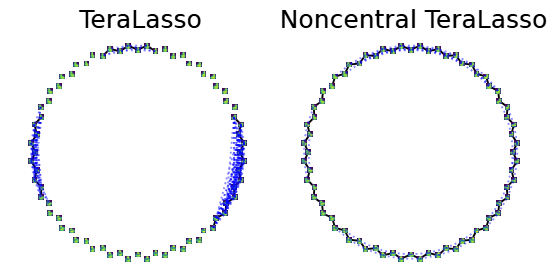
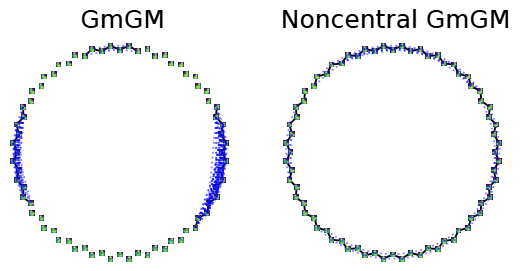
Applying our correction

Part 3

Strong Product Model

2025

https://github.com/BaileyAndrew/Strong-Product-Model

Genes

Cells

 2  ... 10
  :  ...   :
 5  ...  7

Dependency between genes

Dependency between cells

How do these two types of dependency interact?

X

Y

X

Y

Z

The Strong Product differentiate and learns:

  • within-row interaction
  • between-row interaction

Model Choices without independence

\mathbf{X} \in R^{d_1\times d_2}, ~ ~ vec[X]\sim N(\mathbf{0},\Omega^{-1})
O(d_1^2d_2^2)

 single sample   

parameters!

We can impose a specific structure on 

\Omega=\zeta(\Psi_{row},\Psi_{cols})

Genes

Cells

 2  ... 10
  :  ...   :
 5  ...  7

Strong Product model: We add these together!

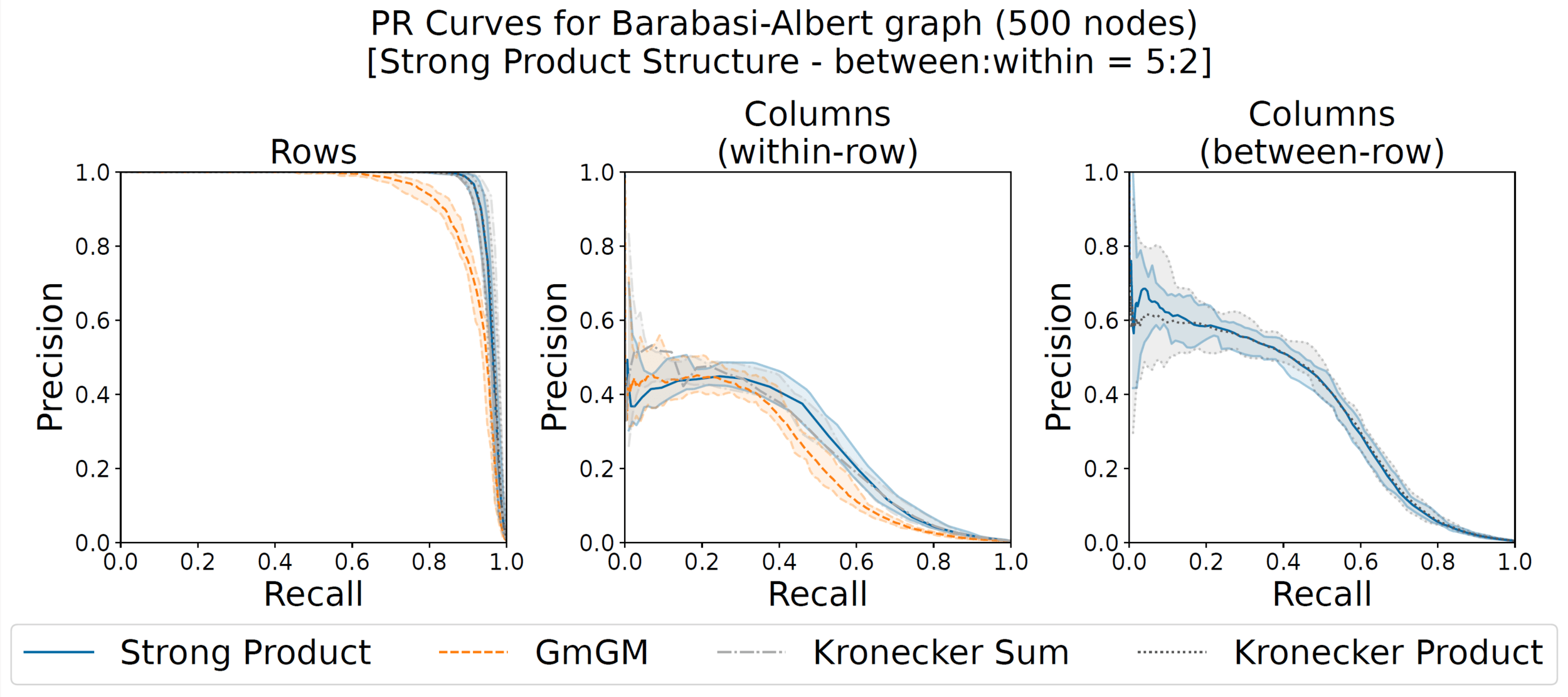
\mathbf{\Psi}_\mathrm{cells} \otimes \mathbf{I} + \mathbf{I}\otimes\mathbf{\Psi}_\mathrm{genes ~ within ~ cells} + \mathbf{\Psi}_\mathrm{cells}\otimes\mathbf{\Psi}_\mathrm{genes ~ between ~ cells}

Synthetic data ground truth

                                                                                         (here y=1, x=2.5)

with A, B, C are Barabasi-Albert random graphs with 500 nodes each

y\mathbf{A} \otimes x\mathbf{B} + y\mathbf{A} \oplus \frac{1}{x}\mathbf{C}

Our Strong Product is the only one that learns both types of column graphs

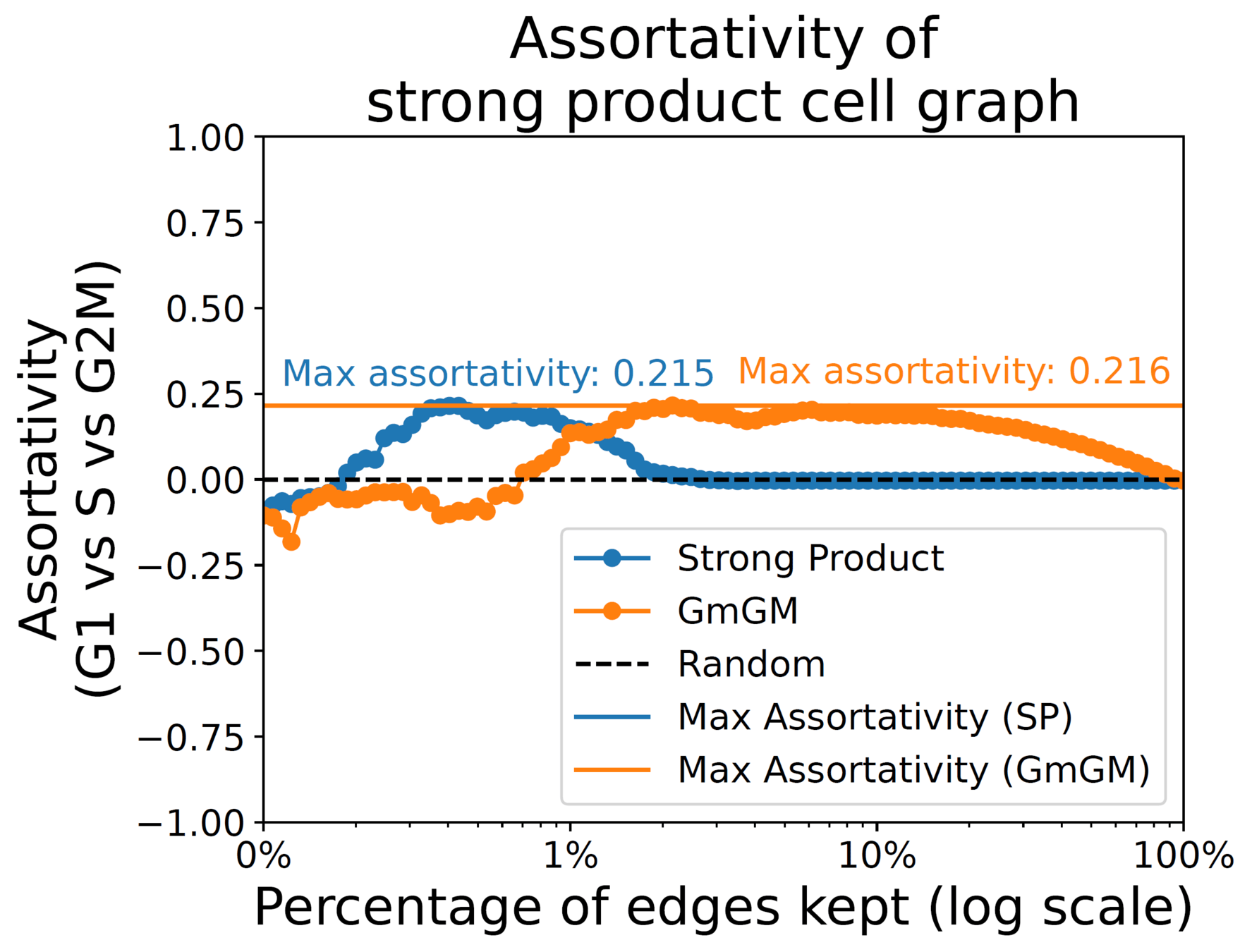
288 mouse embryo stem cell scRNA-seq dataset from Buettner et al. (2015), limited to 167 genes mitosis-related genes cell cycle labelled (G1,S,G2M).

 

Assortativity:

measures tendency of cells within a stage to connect

1 (tend to connect)

0 (no tendency)

-1 (tend not connect)

Results

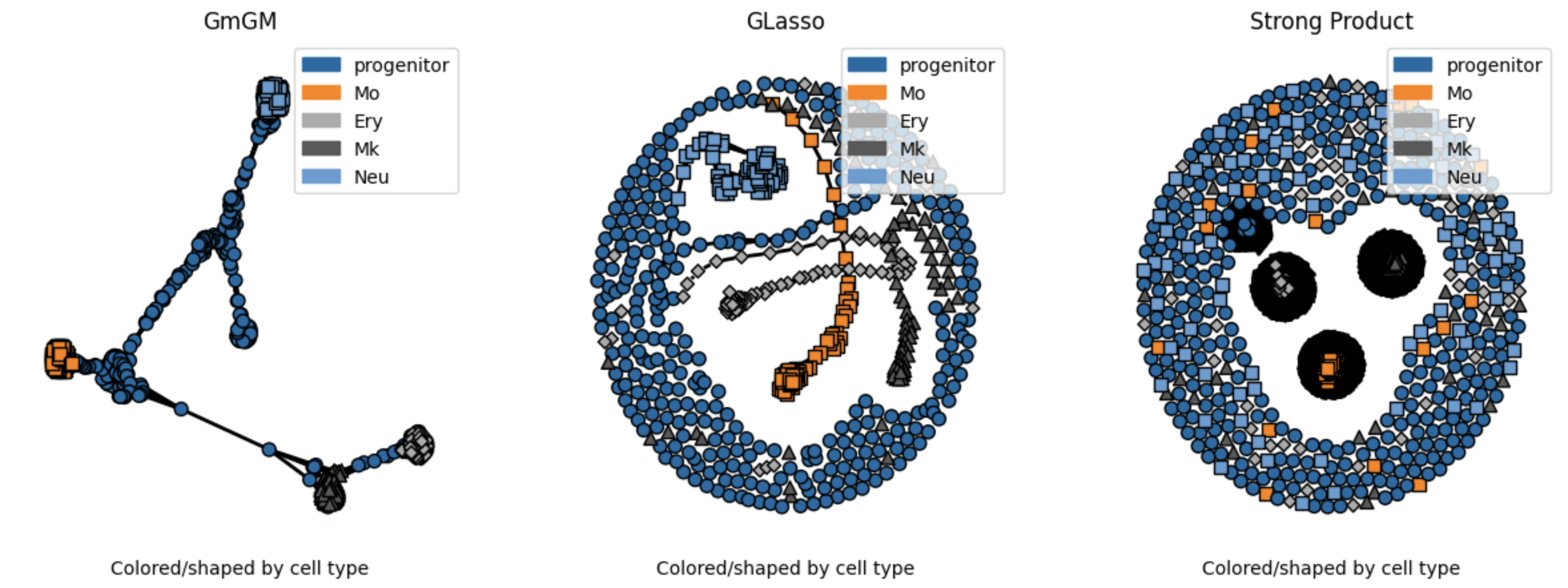
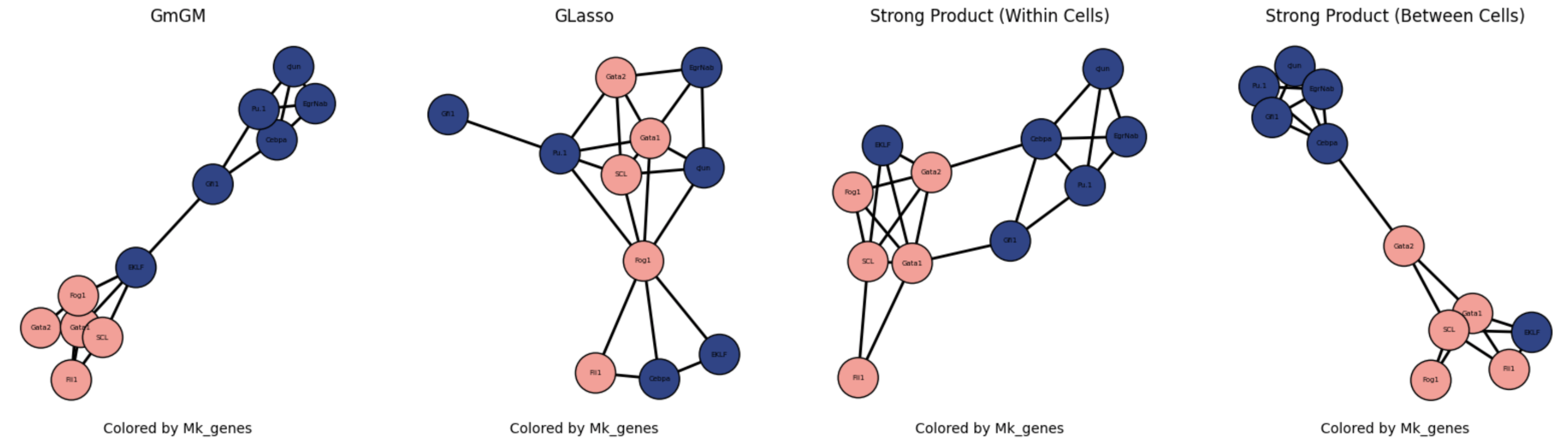
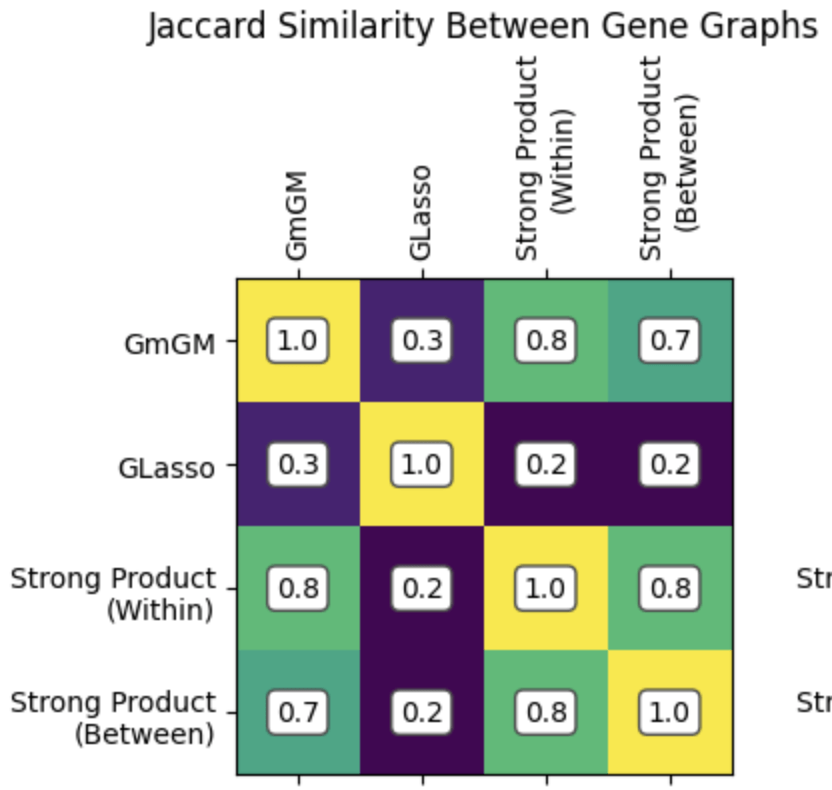
Practical tutorial in github codespaces

Part 4

Instructor: Bailey Andrew, University of Leeds

https://github.com/BaileyAndrew/ellis-summerschool

Practical

  1. Synthetic data (15min)
  2. Getting the most out of GmGM (15min)
  3. Real data (15min)
  4. Open-ended challenges

Ask questions if stuck or curious!