Fun Facts about Networks
Luisa Cutillo
l.cutillo@leeds.ac.uk

Networks


Technological
Social
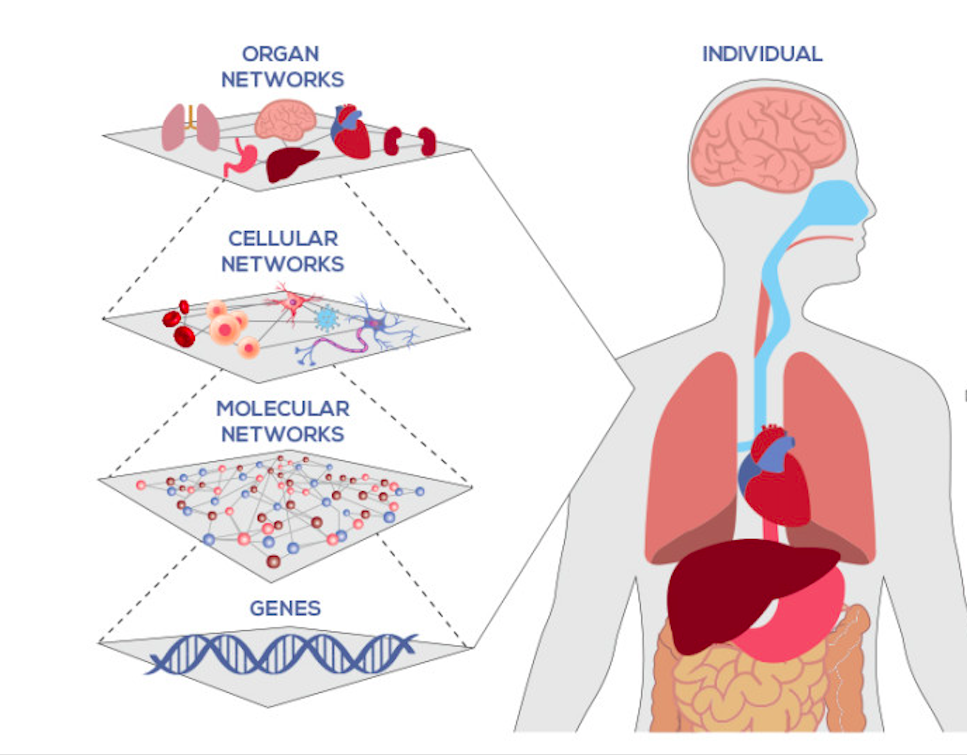
Biological
Real Data Application

Networks in maths
Networks are mathematical representations of interactions among the components of a system and can be modelled by
graphs
- Components: Nodes, Vertices
- Interactions: Links, Edges
- Systems: Network, Graph
- V
- E
- G=(V,E)
A planar graph is one in which the edges have no intersection or common points except at their endpoints.
- planar graph
- non planar
- complete
- both connected
Euler had discovered something peculiar about calculating together the number of vertices, edges and regions
V=number of vertices= 5
E=number of edges= 6
R=number of regions= 3 (the outside region counts!)
V-E+R=2
Let's try again
V=number of vertices= 5
E=number of edges= 7
R=number of regions= 4 (the outside region counts!)
V-E+R=2
Let's try again
V-E+R=2
?
Is it always true?
?
Planar!
Is it always true?
Connected!
The Euler characteristic:
V−E+R
is always 2 in the case of connected planar graphs
Conclusion
A proof by induction is a mathematical proof technique: 1- base case, proves the statement for n = 0 without assuming any knowledge of other cases. 2-induction step, proves that if the statement holds for any given case n = k, then it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. (*base case not necessarily begin with 0, but often with 1 or any fixed number N)
Proof by induction
Proof by induction
V= 1
E= 0
R= 1
V= 1+1=2
E= 0+1=1
R= 1
- true when adding one new vertex connected by one new edge
- true when carving out a new region from part of an old region with the addition of a single new edge
- Since any connected planar graph can be built up in this way by gradually adding new vertices and edges, this argument shows V−E+R=2 for any connected planar graph.
Vn= 3
En= 3
R= 2
Vn+1=Vn +1
En+1=En +1
Rn+1= Rn
Vn+2=Vn+1
En+2=En+1 +1
Rn+2= Rn+1 +1
V-E+R=2 TRUE!
Eulerian Paths
A route that never passes over an edge more than once, allowing for revisiting vertices, is called a Eulerian path.
An Eulerian circuit starts and ends at the same vertex, but an Eulerian path can start and end at different vertices.
Circuit
Path
Eulerian Paths and Circuits
Circuit
Path
- even number of edges at each vertex
(even degree)
- the starting and ending vertices have odd degree
- the other vertices have even degree
Euler’s assertion that a graph possessing such a path has at most two vertices of odd degree was the first theorem in graph theory.
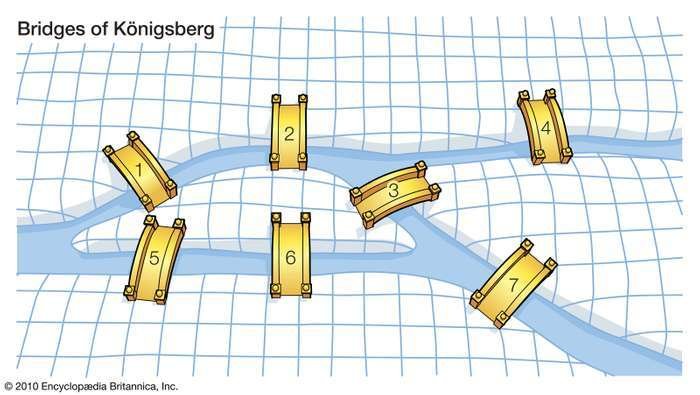
Problem: 7 bridges of konigsberg
Could a person leave home, take a walk, and return, crossing each bridge just once?
A
B
C
D
Problem:
Could a person leave home, take a walk, and return, crossing each bridge just once?
This graph has more than 2 odd vertices!
A
B
C
D

A
B
C
D
Not Eulerian!
Impossible problem!
5 rooms problem:
can you cross each "wall" of the diagram with a continuous line only once?

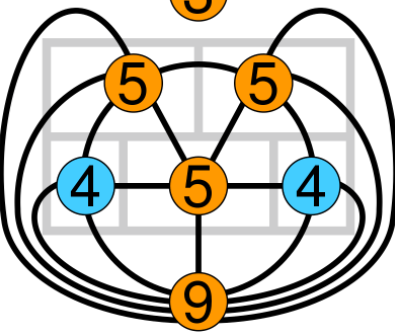
Odd
Even
?